Annealing evolutionary parallel algorithm analysis of optimization arrangement on mistuned blades with non-linear friction

Yuan, Huiqun; Zhao, Tianyu; Yang, Wenjun; Pan, Honggang

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 December 2015

Check for updates

Annealing evolutionary parallel algorithm analysis of optimization arrangement on mistuned blades with non-linear friction

Huiqun Yuan¹

Tianyu Zhao²

Wenjun Yang³

Honggang Pan⁴

¹School of Science, Northeastern University, Shenyang, China

^{2, 3, 4}School of Mechanical Engineering and Automation, Northeastern University, Shenyang, China

⁴Shenyang Institute of Engineering, Shenyang, China

Corresponding Author:

Huiqun Yuan

Cite the article Download PDF

Downloads 1241

Abstract

This paper sets up a lumped parameter model of engine bladed disk system when considering the nonlinear friction damping based on mistuned parameters which is obtained from the blade modal experiment. A bladed arrangement optimization method, namely annealing evolutionary algorithm with tabu list is presented which combines the local search ability of SA (simulated annealing) and the global searching ability of GA (genetic algorithm) introducing tabu list as the search memory list. Parallel TAEA (tabu annealing evolutionary algorithm) is presented based on CUDA (Compute Unified Device Architecture) combining GPU (Graphics Processing Unit) and its performance is analyzed. The results show that optimization based on CUDA framework can improve computing speed. At the same time using optimization results can reduce the amplitude of forced vibration response of bladed disk system and make it in the range of allowable engineering.

1. Introduction

Engine bladed-disk system is symmetric circular cycle structure. There are small differences between actual blades because of the factors of manufacturing error and uneven material quality. This kind of bladed-disk is called mistuning system. The cycle symmetry of bladed-disk is damaged by mistuning. Mode localization and vibration localization of bladed-disk structure are generated further. Vibration amplitude of individual blade is too large and they have a higher fatigue stress. Even lead to fatigue fracture. So it is very important to study on mistuning bladed-disk.

In recent years, many scholars study on the theory of vibration and dynamic characteristics, numerical simulation and experiments of bladed-disk system. For theory firstly, Petrov E. P. [1] analyzed the results of optimum search of mistuning patterns for some practical bladed disks and reveals higher worst cases than those found in previous studies He [2, 3] also presented a near method for the dynamic analysis of mistuned bladed disks and the results of a study looking into changes in the forced response levels of bladed disc assemblies subject to both structural and aerodynamic mistuning. Nikolic M. [4, 5] established whether current mistuned bladed disk analyses should incorporate Coriolis effects in order to represent accurately all the significant factors that affect the forced response levels and introduced robust maximum forced response reduction strategies based on a “large mistuning” concept. On the other hand, in the perspective of simulation Bladh R. [6] explored the effects of random blade mistuning on the dynamics of an advanced industrial compressor rotor, using a component-mode-based reduced-order model formulation for tuned and mistuned bladed disks. Besides, from the point of view of experiment Sever I. A. [7] resulted from an experimental investigation of forced vibration response for a bladed disk with fitted under platform “cottage-roof” friction dampers, together with the corresponding numerical predictions. Finally, Castanier M. P. [8] reviewed the literature on reduced-order modeling, simulation, and analysis of the vibration of bladed disks found in gas-turbine engines.

Through the study it can be found that it is important to reduce the amplitudes of blades. Because of not being limited by temperature and effective simple structure, it is widely used that using friction increases blade damping. Such as flange friction damping block, integral wire or shroud etc. Depending on the degree of simplification of blades, blade friction model can be classified as freedom model of single degree, freedom model of multiple degrees, finite element model and contact friction model. Clear concept, convenience and accurate analytical solution can be got when using freedom model of single degree. But this model is only applicable to small positive pressure case and can’t describe bending-torsion coupling vibration behavior. So it has some limitations [9]. Li Y. [10] simplified bladed-structure as a freedom model of multiple degrees and studied on it. Fang C. [11] used finite element model and expounded new solutions of 3-D vibration effects of modal mistuning strength and pattern, interblade mechanical coupling, and localized modes on the free and forced response amplitudes. Scholars have proposed many mathematical model about the dry friction between two solid surfaces. The complexity of friction process makes it difficult to find a common friction model to explain all the phenomena of friction. Only use different friction model according to the different needs. There are two main types commonly used friction model, namely macro-slip model and micro-slip model. Sanliturk K. Y. [12] model two-dimensional macro friction contact model. Micro-slip model shows that there is slip phenomenon in contact part between friction surfaces before overall slip. Gabor Csaba [13] modelled micro-slip friction damping and considered influence on turbine blade vibrations. Meng C. H. [14] considered the Influence of micro-slip on vibratory response with a new micro-slip model.

Random installation of mistuned blades on the disk can cause large forced vibration amplitude and blade fatigue fracture. So it is important to find optimization arrangement on mistuned blades. At the same time, it is a typical combinatorial optimization problem. From the perspective of accurate solution method, literature [15] used dynamic programming method and literature [16] used branch and bound method. On the other hand, for approximate solution method. Literature [17] a positive approach in an optimized design of a combinatory unified power-quality conditioner (UPQC) and superconducting fault current limiters (SFCLs). In literature [18] quantum-inspired genetic algorithm (QGA) is applied to simulated annealing (SA) to develop a class of quantum-inspired simulated annealing genetic algorithm (QSAGA) for combinatorial optimization. In literature [19], a Simulated Annealing Algorithm (SAA) based heuristic, namely Simulated Spheroidizing Annealing Algorithm (SSAA) has been developed and improvements in the proposed heuristic algorithm is also suggested to improve its performance.

Intelligent optimization algorithm is widely used in recent years. Byeong Keun C. [20] used genetic algorithm in pattern optimization of intentional blade mistuning for the reduction of the forced response. Rahimi M. [21] used genetic algorithm for solving an optimization problem to find the worst-case response of bladed-disk assembly. Li Y. [10] putted forward genetic particle swarm algorithm to optimize the blade arrangement sequence. Kirkpatrick S. [22] used simulated annealing algorithm to solve optimization problem. Yuan H. Q. [23] find optimization of mistuning blades arrangement for vibration absorption in an aero-engine based on artificial ant colony algorithm. Due to the huge solution space of optimization problem. There is no effective method of improving the efficiency of algorithm. The emergence of GPU provides a new train of thought and research direction for improvement of existing algorithms and design of the new algorithm.

In June 2007, NVIDIA published the first piece DirectX 10 GPU and CUDA (Compute Unified Device Architecture). A new module is specially designed for GPU computing. CUDA provides favorable conditions for developers to effectively use of GPU. Since launch, it has been applied widely in many fields. Some techniques for applying GPU computation in FEM (Finite Element Method) were investigated in literature [24], which include element stiffness matrix parallel calculation and global stiffness matrix assembly method, unstructured sparse matrix-vector multiplication and large-scale linear system solving method. In order to accelerate BEM (Boundary Element Method) computation, literature [25] presented a computing unified device architecture based GPU parallel algorithm which is applied in the BEM to solve 3D elastostatics problems. In literature [26] the Cholesky decomposition parallel algorithm based on graphic processing unit was proposed to accelerate the computing speed in the modal calculation program. But almost no scholars apply it into intelligent optimization algorithm to solve the problem of optimization arrangement on mistuned blades.

This article will mainly discuss optimization arrangement on mistuned bladed disk system with flange friction damper. If the number of blades is $n$ , all the calculations are $n!$ When $n$ is a smaller number, all arrangements can be used to calculate. But as $n$ increases, this method will no longer be applied. In this article $n$ is 38, all the calculations come to 5.23×1044. At this time blade arrangement is a typical combinatorial optimization case. Because of large solution space and large amount of calculation, the optimization algorithm is required of time complexity, rapid rate of convergence, high optimization accuracy and the ability to jump out of local optimum. The efficiency of solving such problem is poor when using common intelligent algorithms. So this paper presents annealing evolutionary algorithm, namely combines simulated annealing algorithm and genetic algorithm with tabu list. And the algorithm is innovated by multithreaded parallel mechanism of CUDA. Break through Computational bottleneck of CPU serial mechanism to improve the quality of solutions and solving speed.

2. Micro-slip friction damping model

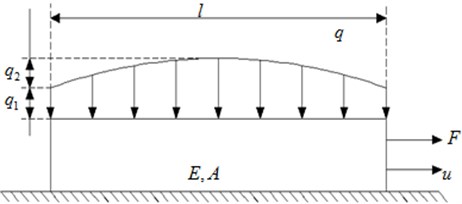
Friction damping block is installed below the bladed-flange. And it works with positive pressure between the damping block and the blade that is provided by centrifugal force. When the blade vibrates, damping block transfers load by friction. And when contact surfaces slips between each other, vibration energy can be consumed by making use of dry friction and vibration stress can be also reduced. So that the blade service life can be improved. Flange friction damper is as shown in Fig. 1. In order to simplify the friction model, the dry friction interface model is simplified as shown in Fig. 2. Namely friction damper is simulated with a rectangular plate pressured in the rigid surface. At the same time that the plate is very thin is assumed, namely positive pressure on the contact surface is equal to that causing by external effect. Normal load $q$ is distributed on the rectangular plate. Rectangular plate right end was composed of blade interaction force $F$ and damper displacement $u$ . Elastic modulus, cross sectional area, length and friction coefficient of the rectangular plate are respectively $E$ , $A$ , $l$ , $μ$ . Further load symmetric distribution form $q (x) = q_{1} + 4 q_{2} (x l - x^{2}) / l^{2}$ is used to simplify the positive pressure.

Fig. 1Flange friction damper

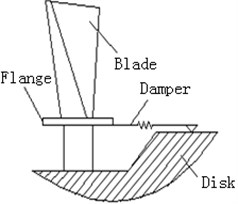
Fig. 2Micro-slip friction model

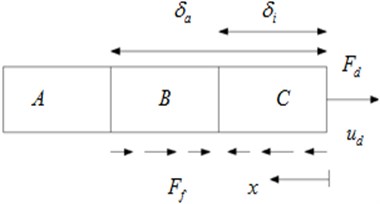
When the damper end force gradually decreases from the maximum and increases from the minimum respectively are as shown in Fig. 3 and Fig. 4. Zone A is in a state of viscous, no slip and zero strain without friction. $δ_{a}$ is slip zone length under the action of forces maximum. In Fig. 3 zone C slips in the direction of $x$ because the force F decreases. And at this time the friction direction is opposite to the direction of $x$ . Zone B keeps the normal strain state in a moment. And at the moment the friction direction fits the direction of $x$ . $δ_{d}$ is compression zone length when the force $F$ reduces. In Fig. 4 Zone C is stretched due to the increase of the force $F$ . And at this time the friction direction fits the direction of $x$ . Zone B keeps the negative strain state in a moment. And at the moment the friction direction is opposite to the direction of $x$ . $δ_{i}$ is tensile zone length when the force $F$ increases.

Fig. 3Applied force reduces from maximum

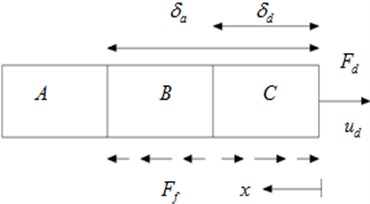
Fig. 4Applied force increases from minimum

When the force acting on the damper varies with extremum, the relationship between the force and displacement on the right side and the slip length are respectively shown as follow:

1

\{\begin{array}{l} F_{d} = - μ N = - μ \int_{0}^{δ_{d}} (q_{1} + \frac{4 (x l - x^{2})}{l^{2}} q_{2}) d x + μ \int_{δ_{d}}^{δ_{a}} (q_{1} + \frac{4 (x l - x^{2})}{l^{2}} q_{2}) d x, \\ u_{d} = - \frac{μ}{E A} \int_{0}^{δ_{d}} (q_{1} + \frac{4 (x l - x^{2})}{l^{2}} q_{2}) x d x + \frac{μ}{E A} \int_{δ_{d}}^{δ_{a}} (q_{1} + \frac{4 (x l - x^{2})}{l^{2}} q_{2}) x d x, \\ F_{i} = - μ N = μ \int_{0}^{δ_{i}} (q_{1} + \frac{4 (x l - x^{2})}{l^{2}} q_{2}) d x - μ \int_{δ_{i}}^{δ_{a}} (q_{1} + \frac{4 (x l - x^{2})}{l^{2}} q_{2}) d x, \\ u_{i} = \frac{μ}{E A} \int_{0}^{δ_{i}} (q_{1} + \frac{4 (x l - x^{2})}{l^{2}} q_{2}) x d x - \frac{μ}{E A} \int_{δ_{i}}^{δ_{a}} (q_{1} + \frac{4 (x l - x^{2})}{l^{2}} q_{2}) x d x . \end{array}

When $δ_{d} = δ_{a}$ or $δ_{i} = δ_{a}$ , the force and displacement on the right side of the damper comes to be a maximum. They are assumed to be $F_{a m p}$ and $u_{a m p}$ :

2

\{\begin{array}{l} F_{a m p} (δ_{a}) = μ q_{1} δ_{a} + \frac{2 μ q_{2}}{3 l^{2}} (3 l {δ_{a}}^{2} - 2 {δ_{a}}^{3}), \\ u_{a m p} (δ_{a}) = \frac{μ {δ_{a}}^{2}}{E A} [\frac{q_{1}}{2} + q_{2} (\frac{4 δ_{a}}{3 l} - \frac{{δ_{a}}^{2}}{l^{2}})] . \end{array}

In order to facilitate amplitude-frequency response characteristics of blades, we need to change the nonlinear characteristics of the damper to a linear case. Lazan linearization method which to be used adopts the idea of equivalent viscous damping. And equivalent ellipse is used to replace hysteresis loop of the relation of the force and displacement. According to the above analysis the equivalent damp and equivalent stiffness of the damper are shown as follow:

3

\{\begin{array}{l} c_{e} (δ_{a}) = \frac{2 E A [{q_{1}}^{2} l^{4} + (4 δ_{a} l^{3} - \frac{14}{5} {δ_{a}}^{2} l^{2}) q_{1} q_{2} + (\frac{8}{7} {δ_{a}}^{4} - 4 {δ_{a}}^{3} l + \frac{16}{5} {δ_{a}}^{2} l^{2}) {q_{2}}^{2}]}{3 π ω δ_{a} {[\frac{q_{1} l^{2}}{2} + q_{2} (\frac{4 δ_{a} l}{3} - {δ_{a}}^{2})]}^{2}}, \\ k_{e} (δ_{a}) = \sqrt{{(\frac{F_{a m p}}{u_{a m p}})}^{2} - {(ω c_{e})}^{2}}, \end{array}

where $ω$ is vibration frequency.

3. Dynamics analysis of bladed-disk system with micro-sliding friction damping

As shown in Fig. 5, flange friction damping force is applied to lumped parameter dynamic model of blade disk system. $m_{i}^{1}$ , $m_{i}^{2}$ and $m_{i}^{3}$ are respectively equivalent mass of the $i$ th sector of blade, blade root and disk. $k_{d i}$ and $k_{b d i}$ are equivalent stiffness of the $i$ th sector disk and mortise. $k_{l i}$ and $c_{l i}$ are equivalent stiffness and damping of the $i$ th blade sector. $F_{i}$ is vibration force of the $i$ th sector. $k_{i}$ is coupling stiffness between each substructure.

Fig. 5Lumped parameter model of bladed-disk system with friction damper

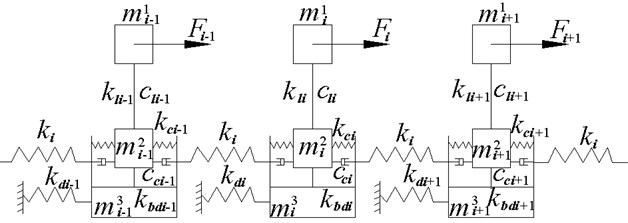
The number of sectors $n =$ 38, namely $i =$ 1, 2,…, 38, dynamic equation of blade disk system is as follow:

4

[M] \{\ddot{X}\} + [C] \{\dot{X}\} + [K] \{X\} = \{F\} .

Assuming that sets the solution of Eq. (4) to be:

5

\{X_{r}\} = {\{X_{1} e^{i ω t}, Z_{1} e^{i ω t}, Y_{1} e^{i ω t}, \dots, X_{38} e^{i ω t}, Z_{38} e^{i ω t}, Y_{38} e^{i ω t}\}}^{T} .

Exciting force is:

6

F_{i} = P_{i} e^{j (ω t + θ_{i})},

where phase angle is $θ_{i} = 2 π E (i - 1) / n$ , vibration frequency is $ω$ , excitation force order is $E$ which is 6. Define the complex stiffness $k_{l f i} = k_{l i} + j ω c_{l i}$ , $k_{c f i} = k_{c i} + j ω c_{c i}$ . Substitution of Eqs. (5), (6) into Eq. (4), yields dynamic equations as:

7

(- ω^{2} [M] + [K_{f}]) \{X_{a}\} = \{P\},

where:

[K_{f}] = [K] + j ω [C], \{X_{a}\} = {\{X_{1}, Z_{1}, Y_{1}, \dots, X_{38}, Z_{38}, Y_{38}\}}^{T},

\{P\} = {\{P_{1}, 0,0, P_{2}, 0,0, \dots, P_{38}, 0,0\}}^{T} .

So it can be derived:

8

\{X_{a}\} = {(- ω^{2} [M] + [K_{f}])}^{- 1} \{P\} .

As $k_{c i}$ and $c_{c i}$ are functions of $δ_{a i}$ , namely [ $K_{f}$ ] is a function of $δ_{a i}$ , [ $X_{a}$ ] is a function of $ω$ and $δ_{a i}$ . By the analytical micro-slip model, $δ_{a}$ is a function of $u_{a m p} (δ_{a i})$ on the physics vibration amplitude $Z_{i}$ of the lumped mass $m_{i}^{2}$ is equal to displacement of damper to the right $u_{i a m p} (δ_{a i})$ , So the maximum length of sliding of the damper can be worked out with iterative method and can the response of each degree of freedom be solved in turn.

4. Establishment and analysis of the algorithm

4.1. Tabu annealing evolutionary algorithm

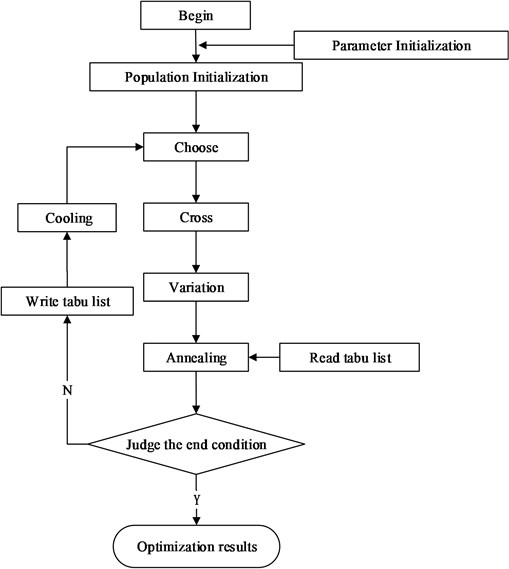
When considering the nonlinear friction damping, the complexity of the model is improved, amount of calculation increases sharply, calculation of the fitness function of each time come to be longer. This requires capabilities that as far as possible to reduce the time complexity of optimization algorithm, to improve convergence speed and at the same time to jump out of local optimal solution. The problem of searching for the best arrangement of mistuned blades is typical quadratic assignment problem. And at the same time QAP is classical combinatorial optimization problem and has been proved as an NP complete problem. It cannot be solved by polynomial time algorithm. When $n >$ 20, it is difficult to find the optimal solution. In order to solve quadratic assignment problem, many heuristic algorithms are used at present. For example, simulated annealing algorithm, genetic algorithm and etc. But the global search ability of SA is insufficient and the efficiency is low. Also the local search ability of GA is insufficient and the algorithm is premature convergence. This paper builds a taboo annealing evolutionary algorithm (TAEA) combining the advantages of both SA and GA. To improve solution group continuously through the mutation operator and selection operator of genetic algorithm, parallel searching is carried out in solution space to converge to global optimal solution quickly. It can help to avoid falling into local optimal solution and facilitate fast convergence to the global minimum that Metropolis process of annealing algorithm is used in the process of solving the problem.

Tabu list of tabu search algorithm is introduced as a short-term memory storage algorithm to avoid searching circularly. To some extent, annealing probability back feature of annealing algorithm can avoid searching circularly. Because there is no memory to record visited the solution set to avoid searching circularly, it leads to slow quality improvement of the solution that sometimes repeat to solve the results which have been calculated in the process of annealing.

Set of the algorithm are as follows:

(1) Coding: In a sequential coding, make it clockwise for blade arrangement direction as a starting point in $x$ axle direction (for position 1).

(2) Crossover operator: Individuals update by crossing with the individual extremum and the global extremum. And the integer crossing method has been used. Firstly, two crossover locations are selected. Then Individuals crosses with the individual extremum and the global extremum.

(3) Mutation operator: random mutation methods of two locations swap is used. Firstly, two mutation locations pos1 and pos2 are selected randomly. Then swap the two blades in the mutation locations.

(4) Tabu list: Because crossover operator and mutation operator are achieved only by the shift of chromosomes, there was a big chance repetitive chromosomes would appear. Annealing process can avoid to visit the solution set that have been solved repetitively by the short-term memory of tabu list. And the speed of the search process can get a certain degree of increase. Hereon, the capacity of the memory table are 25 lines of an array of 25×2, the first column of the two columns are arrangement plans and the second column are the fitness values of the arrangement plans.

Solving process of the algorithm is as follows:

(1) Initialize basic parameters of the algorithm: Such as evolution algebra, initial population, initial temperature and mutation probability, etc.

(2) Comment on the fitness of current group.

(3) Individual crossover and mutation operation.

(4) Produce new individual by the SA state function.

(5) Individual simulated annealing operation (Accept new solutions based on Metropolis Criterion and traverse the taboo table memory. if there is a repetition or a bigger fitness value than the minimum one in the tabu list, return to (4). Otherwise, continue to implement).

(6) Judge the stability of the SA sampling. If instability, return to (4). Otherwise, perform cooling operation after the current solution is written into tabu list.

(7) Execute individual copy operation and keep the best population according to the optimal selection model.

(8) Determine termination conditions. If do not meet the termination conditions, return to (2). Otherwise, output the best currently individual and finish the algorithm.

Fig. 6Flowchart of blade arrangement optimized by annealing evolution algorithm

4.2. Optimization goal and fitness function

In order to increase the influence of friction damping of blade root to vibration localization of mistuned system, the vibration localization factor is put forward as follows:

9

L = \sqrt{\frac{{|x|}_{m a x}^{2} - \frac{1}{n - 1} \sum_{i = 1, i \neq j}^{n} x_{i}^{2}}{\frac{1}{n - 1} \sum_{i = 1, i \neq j}^{n} x_{i}^{2}}},

where, $n$ is the number of blades, $j$ is blade number of the largest amplitude, the largest amplitude is ${|x|}_{m a x}$ . In order to reduce both the overall amplitudes and localization degree of vibration, firstly calculate and draw amplitude-frequency curve of a single blade. With reference to the $N$ key points whose amplitudes change significantly in range of vibration frequency, then calculate the product of mean amplitude and vibration localization factor of every blade and accumulate them. The design of fitness function is as follows:

10

F = \sum_{1}^{N} m e a n (X) \times L,

where $X$ is one dimension vector composed of every blade amplitude, $m e a n (X)$ is the mean value of every blade amplitude and $L$ is blade vibration localization factor. This definition of fitness function give consideration to both overall vibration and vibration localization. Take blade arrangement which makes fitness function minimum for the optimization arrangement.

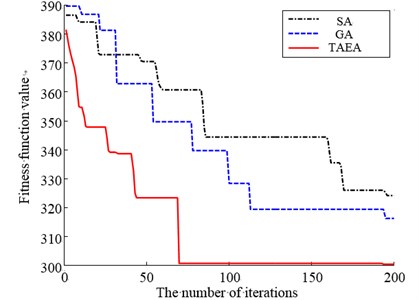
Fig. 7 said fitness values change curves of the optimization process of blade arrangements which simulated annealing algorithm, genetic algorithm and proposed algorithm work for. The figure shows fitness values began to optimizing of the three methods are relatively close. The optimal solution is worse and the convergence speed is slower when simulated annealing algorithm is used. The convergence speed becomes slightly better when genetic algorithm is used. But trap in local optimal solution after 110 iterations and Premature Convergence appears. Because using tabu list effectively avoids the repeated search, converge to an optimal solution after only 65 iterations and get a better solution when proposed algorithm is used. Compared with general algorithm, the efficiency and accuracy when proposed algorithm is used are improved.

Fig. 7Searching procedure comparison

From Fig. 8(a) it can be learnt that the amplitude of number 6, 13, 22 blade is larger than others. This phenomenon conforms to the description of the vibration localization. Fig. 8(c) shows the result which uses optimized configuration scheme. The largest amplitude is only 66.7970 and reduces by 15 % comparing with the largest amplitude 80.1158 of random arrangement. On the other hand Fig. 8(b) shows the vibration of whole work frequency interval. It is easy to find that several amplitudes of many vibration frequency points are larger obviously from Fig. 8(b) when comparing with Fig. 8(d). At the same time the phenomenon of vibration localization appears and the amplitudes in Fig. 8(b) is larger than that in Fig. 8(d). Although a similar phenomenon also appears in Fig. 8(d), the frequency intervals are narrow and localization is not obvious.

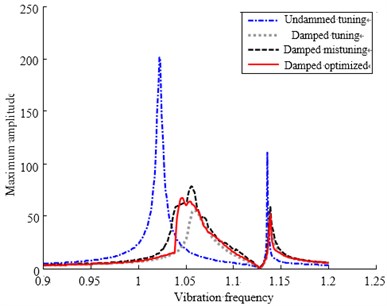
Fig. 9 consists of the maximum bladed amplitude-frequency curve of order arrangement and optimized arrangement. The amplitude-frequency curves of tuning system also appear in Fig. 9 at the same time when consider damping and do not consider it. Thus it can be seen that the amplitudes after optimization are much smaller than that of order arrangement under vibration frequency. The vibration when consider friction damping is far lower than that when do not consider friction damping and even lower than that of tuning system when do not consider friction damping. It stands to reason that the least vibration curve among the four curves is tuning system curve when consider friction damping. The amplitude-frequency curve after optimization is higher than that of tuning system only when frequency is between 1.04 and 1.06. Meanwhile it is lower than that of order arrangement and close to tuning system among other frequency range.

Table 1Comparison of vibration condition under different blade arrangement

Blade arrangement	Mean value	Variance	Maximum amplitude
Order arrangement	27.2664	437.6595	78.3763
Optimized arrangement	40.6697	138.2108	66.5970
Tuning system	35.0523	123.9840	55.5544

To sum up combining with Table 1 that additional nonlinear friction damping can effectively reduce the vibration amplitude. On top of that optimizing arrangement can further improve the system vibration localization phenomenon and be very easy to meet the demand of engineering. The reasonable arrangement can be found by Taboo annealing evolutionary algorithm. The system vibration can be largely reduced. There is still a weak localization phenomenon comparing with tuning system. But it is hard to impact the vibration characteristic of bladed disk system.

Fig. 8Maximum amplitude of forced vibration under blade arrangement optimized comparison

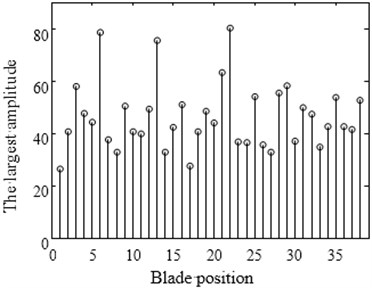
a) Amplitude diagram of random arrangement

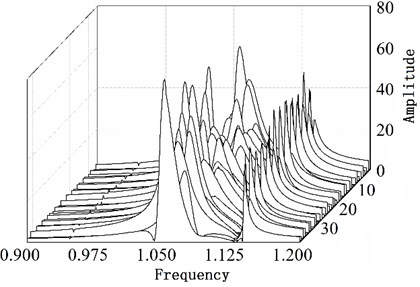
b) Waterfall plot of random arrangement

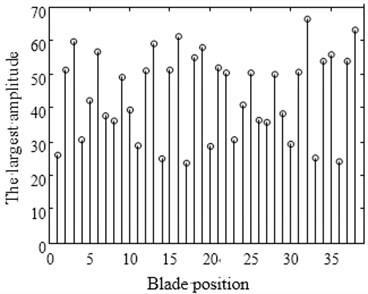
c) Amplitude diagram after optimizing

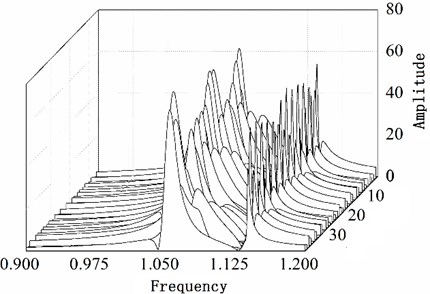
d) Waterfall plot after optimizing

Fig. 9The amplitude frequency curve comparison

5. Optimization analysis based on the CUDA parallel computing

Due to considering the influence of nonlinear friction damping to vibration of the system, computation time of fitness function when using optimization algorithm optimizes lumped parameter model of blade-disk system increases exponentially. Even with algorithm of higher computational efficiency, step length of subcycle is more than 120 seconds. Multi-thread parallel mechanism of CUDA breaks the traditional CPU serial mechanism computational bottleneck. Make calculation more species at the same time using swarm intelligence algorithm possible and provide a new thought of solving portfolio optimization problem. So it will greatly improve the quality of solution and solving speed and breaks CPU serial mechanism computational bottleneck that the transformation and innovation of the algorithm in this paper which is multiple populations parallel computing under the CUDA framework.

5.1. Tabu annealing evolutionary algorithm based on the CUDA framework

Because the calculation of the nonlinear friction damping model is very large, it is required that improving the time efficiency of optimization algorithm and avoiding premature when the optimum algorithm designs. Simulated annealing algorithm has natural advantages for local search. Markov chain has no after effectiveness in the process of constant temperature of annealing algorithm. So the simulated annealing algorithm is very suitable for transformation. On the basis of this paper CPAEA (CUDA Based Parallel Annealing Evolution Algorithm) is designed based on CUDA parallel TAEA algorithm.

First generate initial solution which is composed of $N$ randomly and calculate the fitness value of the initial solution. Then parallel computing of multiple CUDA is carried out Create a new solution for each initial solution respectively and calculate fitness function value again within the scope of the solutions. After that determine whether can accept their respective new solution according to Metropolis Criterion. If accepted, use new solution instead of initial solution to become current solution. Otherwise, still keep current solution invariant to be initial solution of the next time to solve. Repeat aforementioned process until all sampling population are stable at the Markov chain length in the current temperature. Crossover and mutation operator is used again to the optimal solution of all species. First $N$ solutions of highest fitness values is regard as the optimal solution of next cycle. Optimal solution of best fitness value is preserved in the global memory tabu list. Repeat above operation for the second time to start cycle. If optimal solution of the current cycle is superior to the worst solution in the global memory tabu list, replace it. If tabu list has not been fill, the global optimal solution is put at the end of tabu list.

However, it calculates unlike a particle corresponds to a thread. Threads in the same block make up a population. Due to shared memory, access speed is very fast. Thus it has improved the efficiency of the algorithm. Constant temperature process of simulated annealing algorithm needs to go through a cycle of a Markov chain length. If the course of evolution bases on a thread corresponding to an initial solution, it is unable to make this thread cycle operation in parallel and only for serial operation. Further seriously affect the efficiency of the algorithm. So this article chooses to optimize using a thread block for an initial solution. Markov chain cycle computations of the initial solution can be completely parallel. Multiple threads within thread block are scheduled to parallel compute at the same time. It can eliminate the bottleneck of access speed and take better advantage of GPU computation that many provisional results of frequently read and wrote are stored in shared memory of fast access speed. Algorithm holistic framework is as shown in Fig. 10 and processes within each thread are as shown in Fig. 11.

Algorithm detailed steps are described below:

(1) Initialize variables: Take the initial temperature $T_{0}$ , make $T = T_{0}$ , Determine the number of iterations of each $T$ time, namely Markov chain length $L$ . Take $N$ initial solutions arbitrarily $S_{k}$ ( $k =$ 1, 2,…, $N$ ) as operation starting points of $N$ subgroups. Traditional simulated annealing algorithm determines $L$ according to the dimensions of the problem. If the dimensions of the problem is not very large, select small $L$ . This algorithm can determine the number of thread blocks due to the scale of $L$ . The number of thread blocks on low-end GPU of Compute Capability 1.0 is even large. Every grid can also allow 65535×65535 memory block parallel computing. It doesn’t become a bottleneck completely. Bigger $L$ can be chosen for small scale problem. Thereby improve calculation accuracy.

Fig. 10Flow chart of improved TAEA algorithm based on the CUDA structure

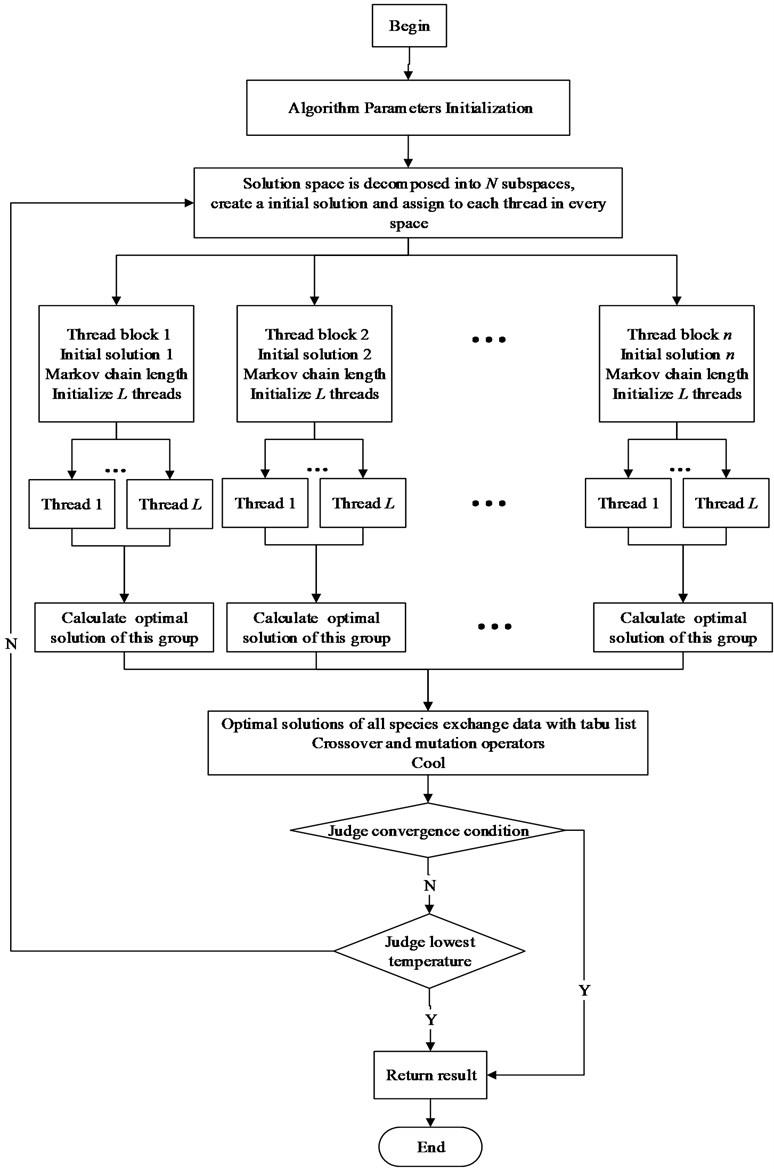
Fig. 11Algorithm flowchart in one thread

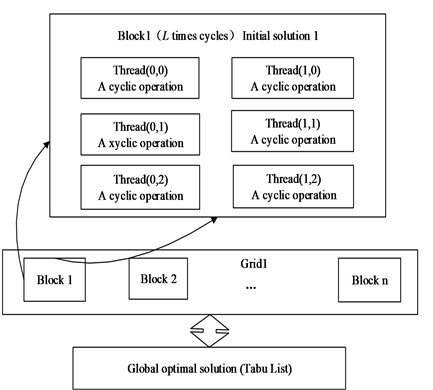
(2) Execute in parallel step (3) and (4) for each thread block of current temperature $T$ at the same time.

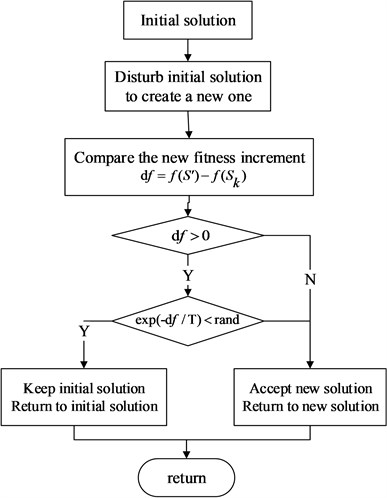
(3) Disturb to create a new solution. Calculate fitness function value of the current solution $S_{k}$ and the new solution $S'$ according to the objective function. Subtract one from another and calculate increment $d f = f (S') - f (S_{k})$ . Crossover and mutation operator can be used to disturb to generated data for discrete problem.

(4) If increment $d f < 0$ , the new solution $S'$ takes the place of the current solution $S_{k}$ as a new current solution. Fitness value of the new solution $f (S')$ is treated as a new current fitness value. Otherwise, accept worse solution at a certain probability according to Metropolis Criterion to avoid algorithm falling into local optimal solution

The formula of Metropolis Criterion is:

11

r = \{\begin{array}{l} 1, & d f < 0, \\ e x p (- \frac{d f}{T}), & d f > 0 . \end{array}

It can be interpreted as: calculate acceptance rate of new solution $r = e x p (- d f / T)$ . If got $r >$ rand, accept $S'$ to be as the new current solution. Otherwise, refuse to data processing and still keep the current solution $S_{k}$ . Where rand is a random number between [0, 1) generated by the CUDA framework.

(5) All the subgroups do data exchange with global memory and do simple crossover operation with the global optimal solution. Update global optimal solution chain table in tabu list.

(6) Gradually reduce the coefficient of temperature control $T$ . If $T$ is still greater than 0, turn to step (2) to continue running.

5.2. Algorithm performance analysis in discrete solution space

Most of combinatorial optimization problems are discrete solution space problems. Capacity of CPAEA algorithm solving the problem of discrete solution space is simulated and verified by traveling salesman problem (TSP). The issues need to be looking for the minimum cost path of single travelers that travel from the starting point, get through all the given requirements demand points, finally turn back to the starting point. Inchoate traveling salesman problem is put forward by Dantzig et al. Traveling salesman problem is one of the most prominent problems in graph theory. Namely given a complete graph of $n$ points, each side has a length. Seek the shortest total length circuits after pass each vertex just once. The mathematical model and algorithm of TSP problem are as follows:

12

C = \{c_{1}, c_{2}, \dots, c_{n}\} .

Assume that $C$ is a collection of $n$ cities. $L = \{l_{i j} (i, j = 1, 2, \dots, n)\}$ is Euclidean distance of $l_{i j}$ . $G = (C, L)$ is a directed graph. The goal for TSP problem is to find the shortest length of Hamilton loop from directed graph $G$ .

So far, no effective algorithms are found for this kind of problem. Tend to accept the guess that there is no effective algorithm for NP-complete problems and NP-hard problems. It is deemed that large instance of this kind of problem cannot use accurate algorithm to solve. And effective approximate algorithm must be sought for this kind of problem. Therefore, TSP problem only exists the known optimal route and no absolute optimal solution. In this paper, the experimental data is obtained from TSP Lib. Choose three different dimensions of classical mathematical model respectively Eil51 model, St70 model and Ch130 model from TSP Lib to solve 30 times for validation. Where the standard simulated annealing algorithm uses traditional way of CPU serial programming.

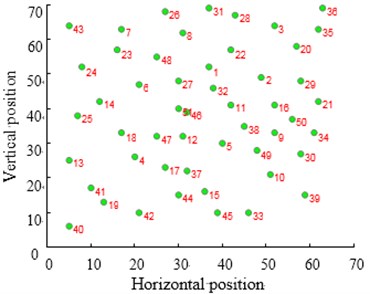
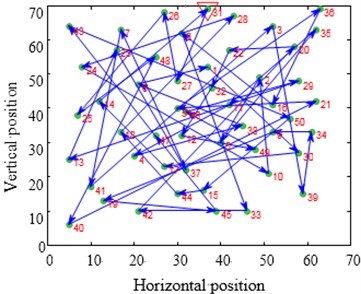
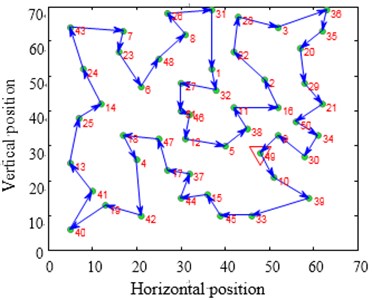
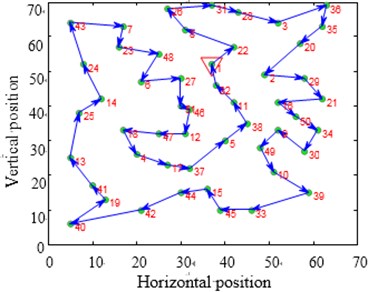
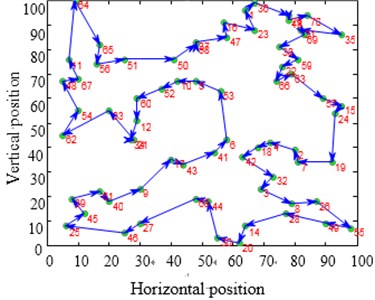
Fig. 12Contrast of solving TSP Eil51 optimization problems

a)

b)

c)

d)

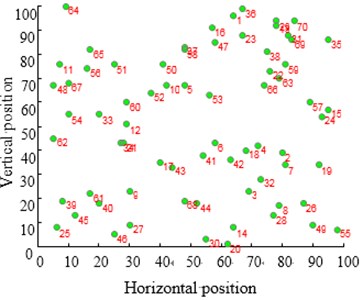
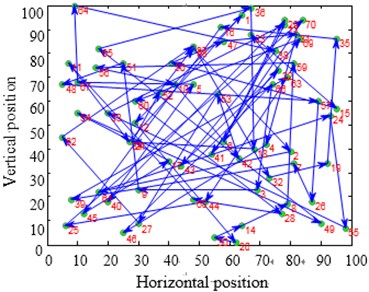
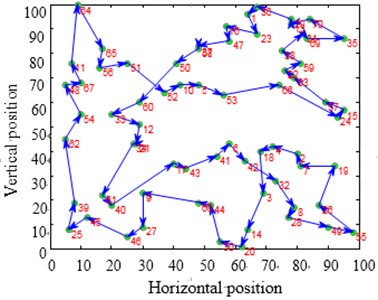
The city distribution of Eil51 problem is as shown in Fig. 12(a). Randomly generate lines as shown in Fig. 12(b). SA and CPAEA are used to calculate 30 times to obtain the best route map as shown in Figs. 12(c) and 12(d) respectively. In order to compare this two kinds of algorithm performance, just set a cycle exit criteria of the temperature limit. Set the same temperature parameters to ensure that these two algorithms have the same cycles. So there is a relatively long horizontal line after both two algorithm convergence. First randomly generate a set of solutions as shown in Fig. 12(b) and its total distance is 1566.0766. Then the total distance of the best optimal solution that use standard genetic algorithm to calculate 30 times to obtain is 451.4131. Further the total distance of the best optimal solution that use algorithm in this paper to calculate 30 times to obtain is 429.9833. CPAEA algorithm have better performance than standard algorithm on the quality of solutions.

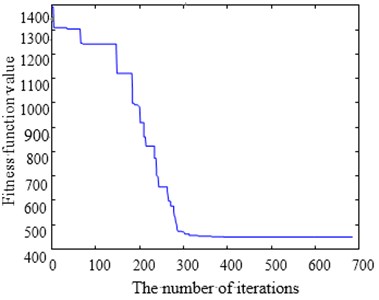
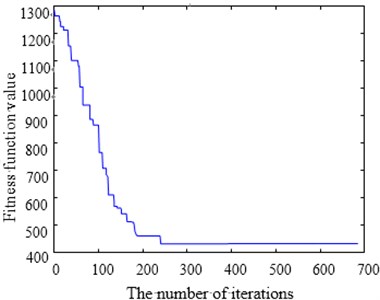
The optimization process convergence curve is as shown in Fig. 13. Fig. 13(a) and Fig. 13(b) are SA convergence curves and CPAEA convergence curves respectively. It is easy to find that CPAEA algorithm converges quickly. Converge to the ideal solution after only 235 iterations. Solving precision is relatively high. But many points of SA convergence curves pause in local optimal solution obviously. Horizontal lines are found at many points of the intermediate solving process.

Fig. 13Optimization convergence curve comparison

a)

b)

Take larger problems St70 model and ch130 model to find the solution respectively. Set the same as the Eil51 model. We can come to a conclusion that CPAEA has the characters of rapid convergence and high precision, no premature phenomenon.

As the problem dimension increases, it can be seen from Table 2 that the advantages of CPAEA are more obvious. Optimal solution has been unable to get for the problem of Ch130 and appear premature phenomenon obviously when using SA. Optimal solution 8535.4918 is even worse than the worst solution when using CPAEA. It can be seen from the standard deviation that the 30 solutions of these three optimization problems when using SA fluctuate wider than that when using CPAEA. The stability of solutions when using CPAEA is also dominant.

Table 2Searching procedure comparison

Solving problem	Algorithm	Optimal solution	Average optimal solution	Standard deviation	Worst solution
Eil51	SA	451.4131	476.1571	13.7173	505.4767
Eil51	CPAEA	429.9833	448.8947	8.7078	462.0087
St70	SA	741.8586	820.5817	65.7088	907.6151
St70	CPAEA	685.6673	738.5235	59.1379	848.6938
Ch130	SA	8535.4918	9367.3631	603.3870	11067.5038
Ch130	CPAEA	6233.5621	7493.8905	482.7096	8518.6986

Time efficiency contrast of the two algorithms is recorded in Table 3 when using CPU serial computations simply and GPU parallel computing. It can be seen that GPU parallel computing time efficiency is higher from the data in the table. And as the dimensions of the problem increases, speedup ratio also increases. 12 times speedup is even obtained when the number of cities amounts to about 130. The advantages of GPU optimization are more apparent in dealing with large scale high latitudes problem. GPU optimization algorithm provides a calculation method which is low cost, high precision and high efficiency when computation time has a high demand.

Table 3Using CPU, GPU optimization time efficiency comparison

Solving problem	CPU optimization	GPU optimization	Speed-up ratio
Eil51	11.7642	1.3736	8.5645
St70	16.0587	1.5176	10.5816
Ch130	26.9874	2.1562	12.5162

Fig. 14Contrast of solving TSP St70 optimization problems

a)

b)

c)

d)

6. Optimization results analysis

Generate two random stiffness mistuning samples. And their standard deviations are 1 % and 5 % respectively. Define as mistuning I and mistuning II.

All the results are summarized in Table 4. Variance reflects fluctuation situation of maximum amplitudes of each blade which is installed in the order according to the optimized results. Mean values give expression to overall vibration situation of the system. Blade vibration situation within a frequency can be observed by amplitude spectra. The following conclusions can be drawn that optimization arrangement on mistuned blades by CPAEA can reduce blade disk system vibration and vibration localization effectively. Don’t need to manual grinding and it can be used directly. Cycle 600 times using the two algorithms in the same way respectively. Treat cycle numbers as the only circulation exit criteria. Compare GPU and CPU computation time, as shown in Table 4.

It can be seen from Table 5 that computation time efficiency of optimization arrangement on mistuned blades based on CPAEA of GPU parallel computing is much better than that based on TAEA of traditional CPU serial computing. The acceleration of 4.5 times can be obtained. It can be completed in only eight hours. In fact, optimization arrangement which could meet application requirements can already be obtained in about 300 times cycles when using CPAEA.

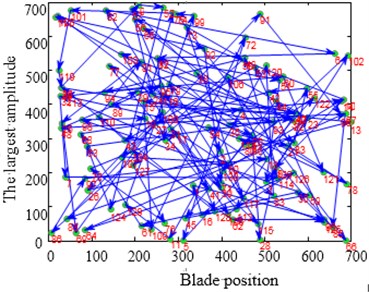
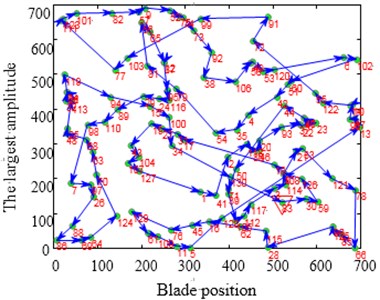
Fig. 15Contrast of solving TSP Ch130 optimization problems

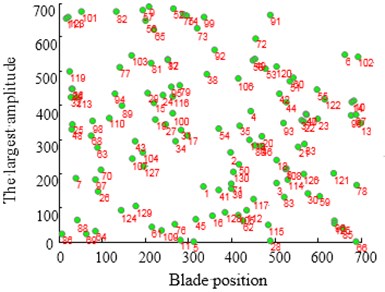
a)

b)

c)

d)

Table 4Comparison of vibration condition under different blade arrangement

Blade arrangement	Mistuning I			Mistuning II
Blade arrangement	Mean value	Variance	Maximum	Mean value	Variance	Maximum
Order	47.3627	165.6697	81.8515	45.6175	350.6177	119.5597
Random	46.9338	160.0796	79.3592	45.7987	330.5540	103.2010
Optimization	45.9033	60.4325	62.4444	45.7381	254.8494	93.9116
Tuning	45.7344	76.0922	55.7577	–	–	–

Table 5Comparison of vibration condition under different blade arrangement

Time	TATA (CPU)	CPAEA (GPU)	Speed-up ratio
Average computation time of single step (second)	230.0442	51.0169	4.5092
Overall computation time (hour)	38.3417	8.5028	4.5092

7. Conclusions

This article constructs concentrated parameter dynamic model of blade disk system considering nonlinear friction damping. The influence of arrangement on mistuned blades to the vibration of blade disk system has been analyzed. Propose the method for optimization arrangement on mistuned blades based on CUDA parallel computing taboo annealing evolutionary algorithm. Research shows that: Proper blade arrangement can reduce forced vibration amplitude and localization of blade disk system effectively. At the same time, it has been proved that method in this paper has advantages which are fast convergence in a large search space, strong local search ability and optimal results. And application of multi-thread parallel computing can improve the calculation efficiency. The results of the study have important guiding significance for reducing the vibration and localization of blade disk system. So this paper has a certain universality and application value for blade arrangement based on the multi-thread algorithm.

References

Petrov E. P., Ewins D. J. Analysis of the worst mistuning patterns in bladed disk assemblies. Journal of Turbomachinery, Vol. 125, 2003, p. 623-631.

Search CrossRef
Petrov E. P., Sanliturk K. Y., Ewins D. J. A new method for dynamic analysis of mistuned bladed disks based on exact relationship between tuned and mistuned systems. Journal of Engineering for Gas Turbines and Power, Vol. 122, 2002, p. 586-597.

Search CrossRef
Petrov E. P., Sayma A. I. Forced response variation of aerodynamically and structurally mistuned turbo-machinery rotors. Proceedings of ASME Turbo Expo 2006: Power for Land, Sea and Air, Barcelona, Spain, 2006.

Search CrossRef
Nikolic M., Petrov E. P., Ewins D. J. Coriolis forces in forced response analysis of mistuned bladed disks. Transactions of the ASME, Vol. 129, 2007, p. 730-739.

Search CrossRef
Nikolic M., Petrov E. P., Ewins D. J. Robust strategies for forced response reduction of bladed disks based on large mistuning concept. Journal of Engineering for Gas Turbines and Power, Vol. 130, 2008, p. 022501.

Search CrossRef
Bladh R., Pierre C., Castanier M. P., et al. Dynamic response predictions for a mistuned industrial turbomachinery rotor using reduced-order modeling. Journal of Engineering for Gas Turbines and Power, Vol. 124, Issue 2, 2002, p. 311-324.

Search CrossRef
Sever I. A., Petrov E. P., Ewins D. J. Experimental and numerical investigation of rotating bladed disk forced response using underplatform friction dampers. Journal of Engineering for Gas Turbines and Power, Vol. 130, 2008, p. 042503.

Search CrossRef
Castanier M. P., Pierre C. Modeling and analysis of mistuned bladed disk vibration: status and emerging directions. Journal of Propulsion and Power, Vol. 22, Issue 2, 2006, p. 384-396.

Search CrossRef
Griffin J. H. A review of friction damping of turbine blade vibration. International Journal of Turbo and Jet Engines, Vol. 7, 1990, p. 297-307.

Search CrossRef
Li Y., Yuan H. Q., Yang S. Optimization on mistuning blades arrangement of vibration absorption based on genetic particle swarm algorithm in aero-engine. Advanced Materials Research, Vol. 655, 2013, p. 481-485.

Search CrossRef
Fang C., McGee O. G., El Aini Y. A reduced-order meshless energy model for the vibrations of mistuned bladed disks, part 2: finite element benchmark comparisons. Journal of Turbomachinery – Transactions of the ASME, Vol. 135, Issue 6, 2013.

Search CrossRef
Sanliturk K. Y., Ewins D. J. Modelling two-dimensional friction contact and its application using hamonic balance Method. Journal of Sound and Vibration, Vol. 193, Issue 2, 1996, p. 511-523.

Search CrossRef
Csaba Gabor Modelling Microslip Friction Damping and its Influence on Turbine Blade Vibrations. Department of Mechanical Engineering, Link Ping University, Sweden, 1998.

Search CrossRef
Meng C. H., Bielak J., Griffin J. H. The influence of micro-slip on vibratory response, part 1: a new microslip model. Journal of Sound and Vibration, Vol. 107, Issue 2, 1986, p. 279-293.

Search CrossRef
Yemets O. A., Roskladka E. V. Solution of a Euclidean combinatorial optimization problem by the dynamic-programming method. Cybernetics and Systems Analysis, Vol. 38, Issue 1, 2002, p. 184-193.

Search CrossRef
Iemets O. O., Yemets Y. M., Parfionova T. A. Solving linear conditional completely combinatorial optimization problems on permutations by the branch and bound method. Cybernetics and Systems Analysis, Vol. 49, Issue 2, 2013, p. 264-278.

Search CrossRef
Heydari H., Moghadasi A. H. Optimization scheme in combinatorial UPQC and SFCL using normalized simulated annealing. IEEE Transactions on Power Delivery, Vol. 26, Issue 3, 2011, p. 1489-1498.

Search CrossRef
Wan N. S. Quantum-inspired genetic algorithm based on simulated annealing for combinatorial optimization problem. International Journal of Distributed Sensor Networks, Vol. 5, Issue 1, 2009, p. 64-65.

Search CrossRef
Anand S., Saravanasankar S., Subbaraj P. Customized simulated annealing based decision algorithms for combinatorial optimization in VLSI floor planning problem. Computational Optimization and Applications, Vol. 52, Issue 3, 2012, p. 667-689.

Search CrossRef
Byeongkeun C. Pattern optimization of intentional blade mistuning for the reduction of the forced response using genetic algorithm. Journal of Mechanical Science and Technology, Vol. 17, Issue 7, 2003, p. 966-977.

Search CrossRef
Rahimi M., Ziaeirad S. Uncertainty treatment in forced response calculation of mistuned bladed disk. Mathematics and Computers in Simulation, Vol. 7, Issue 2, 2009, p. 1-12.

Search CrossRef
Kirkpatrick S. Optimization by simulated annealing. Science, Vol. 220, 1993, p. 671-680.

Search CrossRef
Yuan H. Q., Zhang L. Optimization of mistuning blades arrangement for vibration absorption in an aero-engine based on artificial ant colony algorithm. Journal of Vibration and Shock, Vol. 31, Issue 11, 2012, p. 169-172.

Search CrossRef
Liu X. H., Hu Y. G. Solving large finite element system by GPU computation. Chinese Journal of Computational Mechanics, Issue 1, 2012, p. 146-152.

Search CrossRef
Wang Y. J., Wang Q. F., Wang G. CUDA based parallel computation of BEM for 3D elastostatics problems. Journal of Computer-Aided Design and Computer Graphics, Vol. 24, Issue 1, 2012, p. 112-119.

Search CrossRef
Zhu Bin, Zhang Y. S. Parallel algorithms for modal analysis based on GPU. Journal of Huazhong University of Science and Technology, Vol. 40, Issue 5, 2012, p. 33-36.

Search CrossRef

About this article

Received

10 July 2015

Accepted

28 August 2015

Published

30 December 2015

SUBJECTS

Mechanical vibrations and applications

Keywords

mistuning blade arrangement

nonlinear friction

annealing evolution algorithm

tabu list

GPU

CUDA

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.