Load sharing characteristic analysis of short driving system in the long-wall shearer

1. Introduction

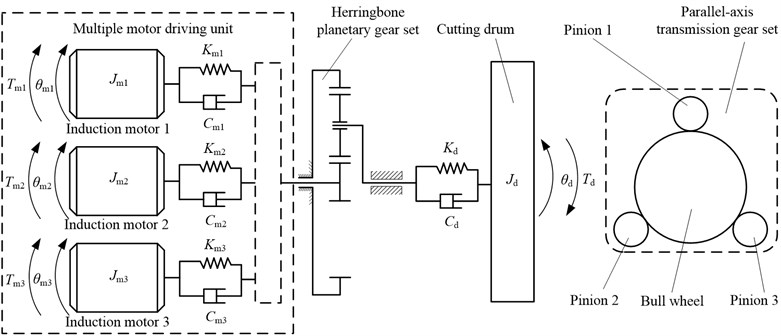
Coal mining is a very complex system and process. The harsh working conditions, hazardous environment and the high international demand for this critical and valuable mining product are the most important factors that affect the coal mining process. Longwall mining, as the most important and applied coal mining methods has many differences from other mining methods because of its high mechanization and productivity [1] and commonly used long-wall mining equipment is made up of midbody, haulage unit, hydraulic system and cutting unit as shown in Fig. 1. The cutting unit is the major component element of long-wall mining equipment, which taking on the task of cutting. The cutting unit is composed of the cutting motor, the gear transmission system, and cutting drum, and the cutting drum interact with coal seam directly. The transmission chain (as shown in Fig. 2) of the cutting unit is so long with several parallel-axis gears and one or two stage of planetary gears. Moreover, the coal seam is usually inhomogenous with hard inclusion and rock intercalation, which induces the following features including heavy load, strong impact and large fluctuation to the cutting drum load. The cutting drum load transfer to the gear transmission system by cutting drum, which will lead to damage of the gears and bearings in transmission system as shown in Fig. 3, and make the coal wining machine stop working. So the gear transmission chain is one of weakest part of the cutting unit. In order to solve this problem, and improve the operational reliability of the coal wining machine, a short driving system (as shown in Fig. 4) in cutting unit was proposed in this paper.

Fig. 1The long-wall shearer

Fig. 2The transmission chain of cutting unit

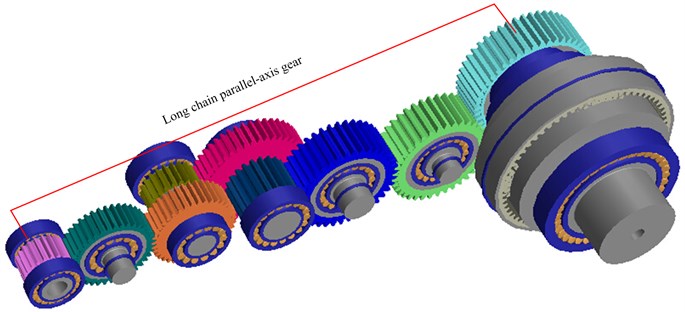
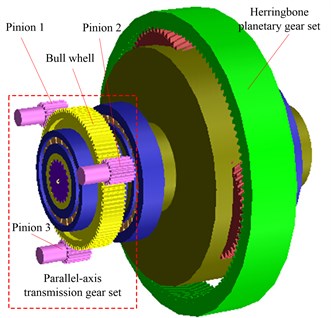
As shown in Fig. 4, the short driving system type of arrangement is also sometimes called a ‘power confluence design’, which is consisting of a multiple motor driving unit (MMDU) and a herringbone planetary gear unit (HPGU). The MMDU is composed of electric motor and parallel-axis transmission gear set and is driven by three or more electric motors via parallel-axis transmission gear set. Then, the cutting drum is driven by the herringbone planetary gear set, which connect with parallel-axis transmission gear set (including three pinions and a bull wheel). Compared with the gear transmission system used in the existing long-wall shearer cutting unit, the short driving system can offer the following advantages:

a) A reduced number of gear stages;

b) Lower energy losses;

c) Increased reliability because of separate drive paths;

d) Fewer gears and bearings;

e) Lower noise levels from gear meshes;

f) Lower overall drive system weight.

In MMDU, the input torque applied should theoretically be shared equally by each transmission path, i.e. each path should carry 1/n of the total input torque [2, 3]. On the one hand, a certain manufacturing errors and assembly variations of components are present; on the other hand, traditional control theory is difficult to meet the performance requirements of control system, especially multiple equipment coordinated system [4]. A synchronous control system is usually used for the MMDU and guarantees the pinions which connect with motor have the same velocity or torque. In practice, the synchronous control system has control accuracy errors existence (namely, the electric motor has synchronization error existence between each other), so it’s hard to make the torque or speed of each electric motor complete identical. By this token, the load sharing performance is very important for the dynamic behavior and failure life of a gear system [5]. The coupling effect between the synchronous error of electric motor and the gears manufacturing eccentricity error or transfer errors etc. extrinsic and intrinsic factor may lead to wear and failure of a gear system because of bad load sharing performance. As a consequence, study the load sharing characteristic of the MMDU is necessary.

Fig. 3The damage bearing and gear

a) The damage bearing

b) The damage gear

The study of load sharing characteristic of gear transmission system for many years and improve load sharing characteristic of gear transmission system is beneficial to slow the wear and tear of gear and enhance the life of gear. The multi-motor-gear system can be considered as the extension of multiple-parallel-transmissions, which have been studied with different approaches, based mainly on gear dynamics [6]. Jing Wei et al. [7-9] developed a dynamic model of multi-gear drive in a tunnel boring machine and the effects of inertia on the driving mechanism and cutter head are considered. The study demonstrates that the load-sharing coefficients at different rotating cutter head speeds and input torques are determined and are found to reach up to 1.2-1.3. A load sharing index was proposed according to the minimum and maximum of the Floquet multipliers and the simplified dynamic model of an example gear system driven by two pinions simultaneously is presented by Haidong Yu [5] et al., in which mechanical parameters such as meshing frequencies, bearing stiffness of pinions, mounting locations of pinions, and gear configuration coefficients are involved. The correlations of the load sharing behavior of every mesh gear pair and the mechanical parameters are discussed. Shaoping Bao [10] et al. developed a nonlinear dynamic model of the multi-motor-gear system and in which non-linearity of gear meshing stiffness, gear geometric and assembly errors, and the motor characteristics are duely considered. A companion study to develop a method to investigate the effects of machining errors, assembly, and tooth modifications on loading capacity, load-sharing ratio, and transmission error of a pair of spur gears by using specially developed finite element method software by Li [11]. Singh and N. Alfred [12-14] have studied static load-sharing performance of planetary transmission with finite element method, then Singh has provided a physical explanation for the basic mechanism causing the unequal load-sharing phenomenon. Ligata et al. [15] have presented a simplified discrete model to predict load sharing among the planets of a planetary gear set with planet carrier position errors and proposed a translational representation of the torsional system that includes any number of planets positioned at any spacing configuration. Ajit Bodas and Ahmet Kahraman [2] have mainly considered the effect of manufacturing errors on the static load-sharing behavior of planetary gear sets and proposed three parameters of the load-sharing coefficient and static load-sharing coefficient describing the load-sharing behavior of the planetary gear trains. Abousleiman and Velex [16] have presented a model which enables the simulation of the three-dimensional dynamic behavior of planetary/epicyclic spur and helical gears. Dynamic load-sharing behavior and load-sharing coefficient of star gear trains with effect of each levels connection stiffness and star gear eccentric errors have been analyzed by Fang et al. [17].

However, current research on the load-sharing characteristic of MMDU takes only the nonlinear coupling factors between the bull wheel and multiple pinions into account, less research has considered the influences of the electric motor intrinsic mechanical property and synchronization error. In this study, firstly, a translation-torsional dynamic model for the parallel-axis transmission gear set of the MMDU is proposed, which is connected to the electric motor model for load-sharing characteristic analysis by the angular displacement. Next, an electromechanical dynamic model for the MMDU is constructed including the electric motor, the parallel-axis transmission gear set and the cutting drum. Then, the load-sharing characteristics are simulated when the shock loads are acted on the cutting drum and the MMDU. By taking into account the electric motor intrinsic mechanical property and synchronization error, the dynamic load-sharing characteristics of the MMDU are analyzed based on the electromechanical dynamic simulation, the influence of manufacturing eccentricity error and transfer error of gears on the load-sharing characteristics are also investigated in order to compare with the electric motor synchronization error. It provides the date support in the gear design and synchronization control of the MMDU. At last, the study contents are reviewed and conclusions are briefly concluded.

Fig. 4The short driving system

2. Model of the electric motor

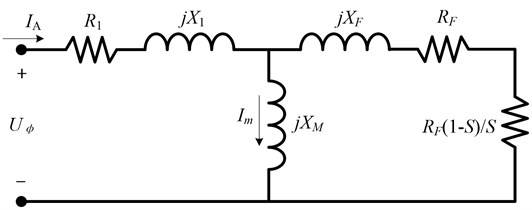
The steady-state model of electric motor is used in the electromechanical dynamic analysis. The steady-state model of driving motor, namely, the intrinsic mechanical characteristic of electric motor reflects the relationship of the output rotation speed and the output torque of electric motor. The intrinsic mechanical characteristic of electric motor [18] is derived by steady-state equivalent electric circuit of electric motor as shown in Fig. 5. The intrinsic mechanical characteristic of electric motor is derived as Eqs. (1) and (2):

Combined with Eqs. (1) and (2), electromagnetic torque can be found as Eq. (3):

where $T_e$ is the electromagnetic torque of electric motor; $P_e$ is the power of electric motor; $I_2^{\text{'}}$ is equivalent rotor current value; $m_1$ is phase number; ${\mathrm{\Omega }}_s$ is synchronous angular speed; $U_{\varphi }$ is phase voltage; $R_1$ is stator resistance; $R_F$ is equivalent rotor resistance; $j{X}_1$ is stator leakage reactance; $j{X}_F$ is equivalent rotor leakage reactance; $j{X}_M$ is the magnetizing inductance; $s$ is slip ratio.

Fig. 5The equivalent circuit of this induction motor

3. Dynamic model of parallel-axis transmission gear set

The dynamic mathematic model of the parallel-axis transmission gear set is established by using centralized parameter method. The translation-torsional equivalent dynamic model of the parallel-axis transmission gear set is shown in Fig. 6.

Fig. 6Equivalent dynamic model for the translation-torsion of parallel-axis transmission gear set

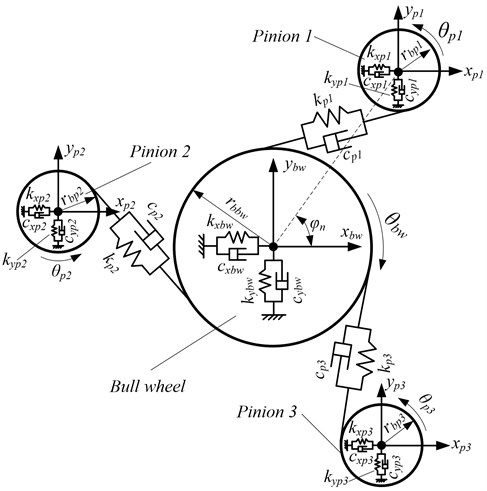
Fig. 6 illustrated the equivalent dynamic model of the parallel-axis transmission gear set; each component of the parallel-axis transmission gear set is regarded as a rigid body. The elastic deformation of support shafts, bearings and gears are represented by equivalent spring stiffness and damping among which $k_{pi}\left(t\right)$ represents the time-varying mesh stiffness and $c_{pi}\left(t\right)$ ($i=$1,…, $N$ and $N$ is the number of pinions) represents the time-varying mesh damping between pinions and bull wheel. $k_{xpi}$, $k_{xbw}$ and $k_{ypi}$, $k_{ybw}$ ($i=$1,…, $N$ and $N$ is the number of pinions) represent support equivalent spring stiffness of pinions and bull wheel in $x$-direction and $y$-direction, respectively, $c_{xpi}$, $c_{xbw}$ and $c_{ypi}$, $c_{ybw}$ ($i=$1,…, $N$ and $N$ is the number of pinions) represent support equivalent spring damping of pinions and bull wheel in $x$-direction and $y$-direction, respectively. $r_{bpi}$ and $r_{bbw}$ respectively represent the base circle radius of the pinions and bull wheel. ${\phi }_n$ is the position angle of the theoretical center of $n$th pinion, where ${\phi }_n=2\pi \left(n-1\right)/N$.

The system in Fig. 6 has (3$N+$3) degree of freedom, where $N$ is the number of pinions. The generalized vibration displacement is $X=\left(x_{pi},y_{pi},{\theta }_{pi,}{x}_{bw},y_{bw},{\theta }_{bw}\right)$, where $x_{pi}$, $x_{bw}$, $y_{pi}$, $y_{bw}$ and ${\theta }_{pi}$, ${\theta }_{bw}$ donate $x$-direction, $y$-direction translational displacement and angular displacement of pinions and bull wheel, respectively.

Supposing the relative dynamic displacements along the meshing line in each pinion and bull wheel are ${\delta }_i$ ($i=$1,…, $N$ and $N$ is the number of pinions), the gear time-varying stiffness $k_{pi}\left(t\right)$ and the dynamic meshing forces $F_{pi}$ can be calculated according to [19, 20]. The differential equation of equivalent mathematic model is:

where $m_{pi}$, $m_{bw}$ and $J_{pi}$, $J_{bw}$ are the mass and moments of inertia of the pinions and bull wheel, respectively.

The load distribution between pinions and bull wheel are affected by the errors, which are manufacturing eccentric error of pinions $E_{pi}$ and manufacturing eccentric error of bull wheel $E_{bw}$, transmission error of pinions $A_{pi}$ and transmission error of bull wheel $A_{bw}$. The equivalent accumulated meshing error caused by the errors which are mentioned in the above, along with the meshing line can be defined as follows according to [8, 21]:

where ${\alpha }_t$ is the meshing angle and ${\phi }_i$ is the azimuth angle of each pinion. In this paper, the MMDU is driven by three electric motors and the motors are evenly distributed, ${\phi }_i=2\pi \left(i-1\right)/3$. $\gamma$ and $\beta$ are the phase angles of manufacturing eccentric error and transmission error. ${\omega }_{pi}$ and ${\omega }_{bw}$ represent the angular velocity of pinion and bull wheel, respectively.

4. Electromechanical dynamic model of the short driving system

The electromechanical dynamic model of the short driving system as shown in Fig. 7, which is composed of electric motors, the parallel-axis transmission gear set, herringbone planetary gear set and the cutting drum. In this paper, the load-sharing characteristic of the MMDU of the short driving system will be studied, so an electromechanical dynamic model of the MMDU is constructed including the electric motors, the parallel-axis transmission gear set and the cutting drum, where the planetary set is simplified to a rotary inertia $J_p$ and a transmission ratio $i_p$ due to the load-sharing coefficient of first stage planetary system has no effect on the load-sharing coefficient of the other stage for multi-stage planetary system [9]. In Fig. 7, $T_{mi}$, $J_{mi}$ and ${\theta }_{mi}$ ($i=$1, 2, 3) are the torque acting on the electric motor rotor, the rotary inertia and angular displacement of the electric motor rotor. $T_d$, $J_d$ and ${\theta }_d$ are the torque acting on the cutting drum, the rotary inertia and angular displacement of the cutting drum. $K_{mi}$ and $K_d$ are the connecting stiffness between the electric motors and the pinions, $C_{mi}$ and $C_d$ are the connecting damping between the electric motors and the pinions, respectively.

Fig. 7Electromechanical dynamic model of short driving system

The torque acting on the electric motor rotor ($T_{mi}$) can be calculated by Eq. (3), the torque acting on each pinion ($T_{pi}$) and bull wheel ($T_{bw}$) in Eq. (4) can be obtained by Eqs. (6) and (7). The differential equation of the cutting drum is derived as Eq. (8). The differential equation of the electric motor is derived as Eq. (9). The electromechanical model can be constructed with Eqs. (4), (8) and (9):

5. Solution of load-sharing coefficient

In what follows, the load-sharing characteristic of the MMDU will be studied which use the developed electromechanical dynamic model, with interests in the influences of the electric motor synchronization error, manufacturing eccentric error and transmission error. Here, the load-sharing coefficient is a measurement index for load uneven level in each pinion at a certain time. The load-sharing coefficient in each tooth frequency cycle can be calculated as [8]:

where ${\lambda }_{pij}$ is the load-sharing coefficient in each tooth frequency cycle; $i=1-N$ and $j=1-n$ ($n$ is the number of tooth frequency cycle in one system period). The dynamic meshing forces $F_{pi}$ can be calculated according to [19, 20].

Define the load-sharing coefficient in one system period as:

where ${\kappa }_{pi}$ is the load-sharing coefficient in one system period.

6. Simulation and analysis

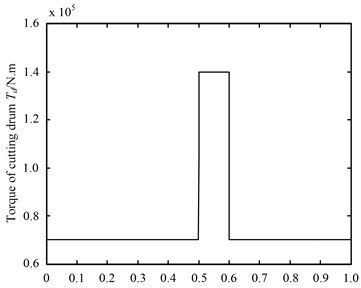
The coal seam is usually inhomogenous with hard inclusion and rock intercalation, which induces the shock load on the driving system, so the load-sharing characteristics of system are simulated under shock load with different electric motor synchronization error, different manufacturing eccentric error and different transmission error. The shock load is a transient process when coal winning machine is working, so in order to investigate the effect of each error which mentions above on the load-sharing characteristic of MMDU under the action of the shock load, a square signal is used to simulate the load mutation process which is acting on the cutting drum, as shown in Fig. 8. The shock load starts at 0.5 s and ends at 0.6 s with the amplitude is 70 KN. the parameters of the multiple motor driving system are shown in Table 1.

Fig. 8Torque acting on the cutting drum

The supporting damping, torsional damping and meshing damping can be obtained as follows:

where ${\zeta }_S$ is the flexural damping ratio of material, the value is 0.03-0.1; ${\zeta }_T$ is the torsional damping ratio of material, the value is 0.005-0.075; ${\zeta }_V$ is the meshing damping ratio, the value is 0.03-0.17.

6.1. Effect of synchronization error on load-sharing coefficient and dynamic load

The load-sharing coefficients are not same under different synchronization error of electric motor when master slave control method is used in MMDU of the short driving system, which imply that the torque acting on each pinion is different. Synchronization error is defined as the ratio of the difference value of the output torque of master motor and slave motor to the output torque of the master motor. A value of 0 represents the output torque of slave motor equal to the output torque of master motor, a value greater or less than 0 represents the output torque of slave motor less or higher than master motor. The load-sharing coefficients of MMDU can be obtained using Runge-Kutta integration method based on electromechanical dynamic model (as shown in Fig. 7).

Fig. 9Load-sharing coefficient and dynamic meshing force with synchronization error of 10 %

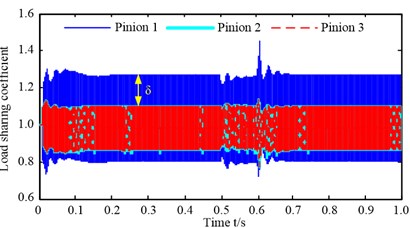
a) Load-sharing coefficient

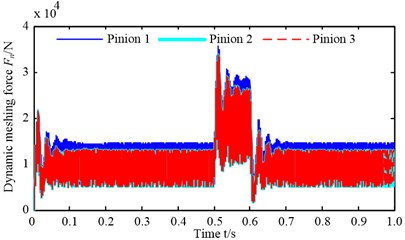
b) Dynamic meshing force

Load-sharing coefficient and dynamic meshing force with synchronization error of 10 % is shown as Fig. 9 when the steady-state electric motor model is used and the initial rotating speed of the electric motor is set as the rated speed. According to Fig. 9, the load-sharing coefficient of pinion 1 is greater than the load-sharing coefficient of pinion 2 and 3, $\delta$ represents the difference value of load-sharing coefficient between pinion 1 and other two pinions; but the load-sharing coefficient of pinion 2 and 3 is nearly equal, as shown in Fig. 9(a). This is to say, the dynamic meshing force acting on pinion 1 is greater than the dynamic meshing force acting on pinion 2 and 3, and the dynamic meshing force acting on pinion 2 and 3 is almost equal, which can be proved by calculating the dynamic meshing force ( as shown in Fig. 9(b)) of each pinion. The reason for this phenomenon is that the output torque of the electric motor which connects with pinions are different as shown in Fig. 10; it is obvious that the output torque of electric motor 1 (master motor) is greater than electric motor 2 and 3 (salve motor), and the output torque of electric motor 2 and 3 is almost equal.

Fig. 10The output torque of electric motor with synchronization error of 10 %

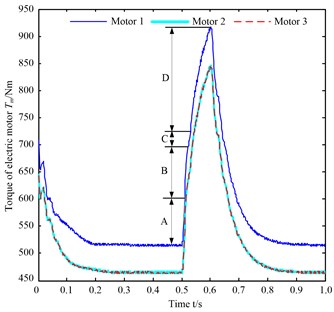
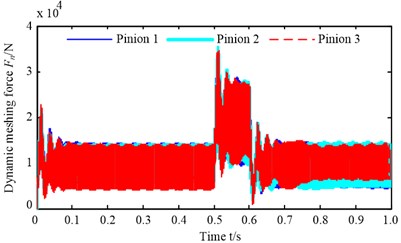
As shown in Fig. 9(a), 0.5-0.6 s shows the load-sharing coefficient under the shock load, the load-sharing coefficient of each pinion has a nonlinear fluctuation process before stable. This is because the difference value of the output torque between electric motor 1 and electric motor 2 and 3 has a decrease and increase process (as the area A, B, C and D shown in Fig. 10) during 0.5-0.6 s. The maximum load-sharing coefficient of pinions is 1.453 at 0.6 s, because the difference value of the output torque between the electric motor 1 and the electric motor 2 and 3 reach the maximum value. And a similar process can be observed after the shock load; this is also because the difference value of the output torque between electric motor 1 and electric motor 2 and 3 has a decrease and increase process during 0.6-0.7 s. As shown in Fig. 9(b), 0.5-0.6 s shows the dynamic meshing force variable process under the shock load. The dynamic meshing force begins to increase immediately at the beginning of the shock load, and does not reach the steady state until the end of the shock load. The dynamic meshing force begins to decrease promptly and reaches the steady state quickly at the end of the shock load. The similar rules also can be obtained when the synchronization error of electric motor changes from 0 to 50 %, and need not be repeated here.

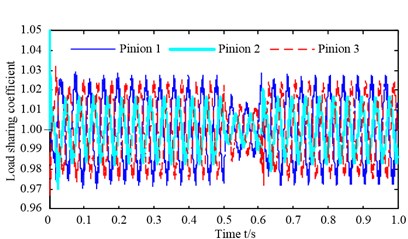
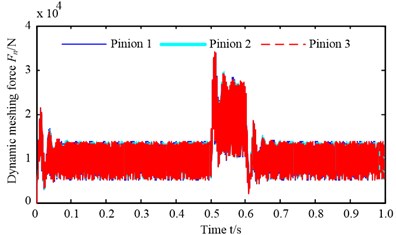
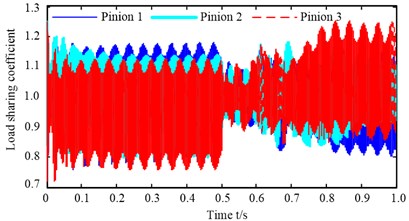
Fig. 11The influence of manufacturing eccentric error on load-sharing coefficient and dynamic meshing force as shown in a) and b), separately, and the influence of transmission error on load-sharing coefficient and dynamic meshing force as shown in c) and d), respectively

a) Load-sharing coefficient

b) Dynamic meshing force

c) Load-sharing coefficient

d) Dynamic meshing force

6.2. Effect of manufacturing eccentric error/transmission error on load-sharing coefficient and dynamic load

In order to compare the influence of manufacturing eccentric error/transmission error on load-sharing coefficient and dynamic load with the influence of electric motor synchronization error on load-sharing coefficient and dynamic load, only the manufacturing eccentric error/transmission error of pinions is assumed to change in the case where the manufacturing eccentric errors/transmission errors for other components are assumed to be constant as 0 μm and the electric motor synchronization error is 0, as given in Eq. (5). Fig. 11 represents the variation of the MMDU load-sharing coefficients and dynamic meshing force with the manufacturing eccentric error/transmission error of pinions is 20 μm, that case will be analyzed as follow.

It can be seen from Fig. 11(a) the load-sharing coefficient appears cyclical change under the function of manufacturing eccentric error, and the maximum load-sharing coefficient of pinion 1 is slightly greater than other two pinions under the steady state, which means the dynamic meshing force of the meshing pair 1 is approximately above the dynamic meshing force of other two meshing pairs as shown in Fig. 11(b). The fluctuation amplitude of the load-sharing coefficient decrease quickly at the beginning of the shock load; and the fluctuation amplitude of the load-sharing coefficient increase immediately at the end of the shock load. The variation of load-sharing coefficient is mainly caused by the sudden increase of dynamic meshing force according to Eq. (10). The dynamic meshing force shows the opposite variation rules compare with the load-sharing coefficient, as shown in Fig. 11(b). Namely, the dynamic meshing force begins to increase immediately at the beginning of the shock load, and does not reach the steady state until the end of the shock load. The dynamic meshing force begins to decrease promptly and reaches the steady state quickly at the end of the shock load.

The similar phenomenon also can be seen in Fig. 11(c) and (d) under the function of transmission error, but the maximum load-sharing coefficient of pinion 3 is lower than other two pinions before the shock load and greater than other two pinions after the shock load. This is because the output torque of the electric motor 3 is greater than the output torque of the electric motor 1 and 2 after the shock load.

Fig. 12The relationship between the RMS of load-sharing coefficient and different errors

a) The relationship between the RMS of load-sharing coefficient and synchronization error

b) The relationship between the RMS of load-sharing coefficient and eccentric error

c) The relationship between the RMS of load-sharing coefficient and transmission error

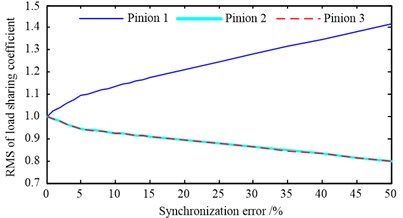
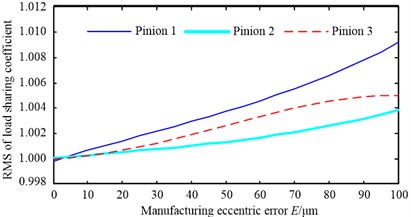
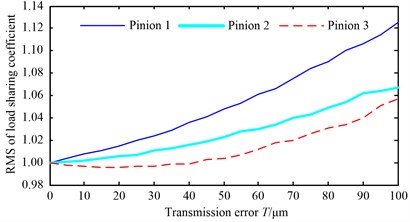
Fig. 12 shows the relationship between the root mean square (RMS) of load-sharing coefficient of system and the three errors (the electric motor synchronization error, manufacturing eccentric error and transmission error) as discussed above. Here, the RMS of load-sharing coefficient will be used to investigate the effect degree of the electric motor synchronization error, manufacturing eccentric error and transmission error of pinions on the load-sharing characteristic of the MMDU.

From Fig. 12(a), it can be observed that the RMS of load-sharing coefficient of system obviously increases with the synchronization error of electric motor goes up. In other words, as the synchronization error of electric motor increases, the load distribution situation among different pinions will become worse. From Fig. 12(b) and (c) respectively, it can be found that the RMS of load-sharing coefficient of system increases with the manufacturing eccentric error and transmission error go up, but the amplification of RMS is not obvious compared with the synchronization error of electric motor. Meanwhile, comparing Fig. 12(a), (b) and (c) can be found that the influence of the electric motor synchronization error on the RMS of load-sharing coefficient is greater than the influence of the other two errors (manufacturing eccentric error and transmission error) on the RMS of load-sharing coefficient, and the influence of the transmission error on the RMS of load-sharing coefficient is greater than the influence of the manufacturing eccentric error on the RMS of load-sharing coefficient. So it is concluded that synchronization error of electric motor has an significant effect on the load-sharing characteristic of system, decreasing the synchronization error of electric motor can improve the load-sharing characteristic of system as shown in Fig. 12(a); and the synchronization error must be controlled under 5 % to ensure the load-sharing coefficient of the MMDU under 1.1. Decreasing the manufacturing eccentric error and transmission error also can improve the load-sharing characteristic of system as shown in Fig. 12(b) and (c), but the effect is unobvious compared with reducing the synchronization error of electric motor.

7. Conclusions

An electromechanical dynamic model for MMDU has been established to study the effect of the synchronization error of electric motor, manufacturing eccentric error and transmission error of pinions on load-sharing performance and dynamic load. Then the main conclusions are:

1) The shock load has less effect on the load-sharing characteristic of MMDU with only considering the synchronization error of electric motor, or manufacturing eccentric error of pinions, or transmission error of pinions. But it has significant effect on dynamic meshing force of gear meshing pair. The dynamic meshing force begins to increase immediately at the beginning of the shock load, and does not reach the steady state until the end of the shock load. The dynamic meshing force begins to decrease promptly and reaches the steady state quickly at the end of the shock load.

2) The RMS of load-sharing coefficient increases with the errors go up, the load distribution situation among different pinions will become worse. And the influence of the electric motor synchronization error on the load-sharing characteristic of MMDU is greater than the influence of the transmission error on the load-sharing characteristic of MMDU, and the influence of the manufacturing eccentric error on the load-sharing characteristic of MMDU is lower than the influence of the transmission error on the load-sharing characteristic of MMDU.

3) The electric motor synchronization error has significant effect on the load-sharing characteristic of MMDU. The load-sharing coefficient evidently increases with the electric motor synchronization error go up, decreasing the electric motor synchronization error can improve the load-sharing characteristic of MMDU, and the synchronization error must be controlled fewer than 5 % to ensure the load-sharing coefficient of the MMDU under 1.1.