Study on nonlinear detection and identification for rubber isolation bearing

3.1. Mechanical modeling of isolation bearing

Rubber isolation bearing, made of super-elastic material, has high hysteretic nonlinear mechanical properties. In this paper, the simplified Bouc-wen model is used to simulate the dynamic response behavior of rubber isolation bearing [8].

Motion equation of SDOF isolation bearing subject to an earthquake acceleration ${\ddot{x}}_g\left(t\right)$ given by:

where, $x$ is the relative displacement, $r(x,x)=F_c\left(\dot{x}\right)+F_s\left(x\right)$ is the total restoring force, $F_c\left(\dot{x}\right)=c\dot{x}$, The Bouc-wen model will be used for $r(x,\dot{x})$ as follows [5]:

where, $\dot{r}=\dot{r}(x,\dot{x})$, $c$ is the damping coefficient, $k$ is the equivalent stiffness, $\beta \text{,}$$\gamma \text{,}$$n$ are hysteretic parameters.

3.2. Nonlinear identification

To identify nonlinear model parameters, Based on a third-order corrector method, the incremental component of $r_k$, $r_{k-1}$ can be expressed:

An observation equation is defined as:

where, ${\mathbf{\theta }}_k=[c,k,\beta ,\gamma {]}^T$ is the unknown parameter vector, ${\mathbf{\epsilon }}_k$ is measurement noise vector, ${\mathbf{\varphi }}_k=\left[{\mathbf{\varphi }}_{k,1},{\mathbf{\varphi }}_{k,2},{\mathbf{\varphi }}_{k,3},{\mathbf{\varphi }}_{k,4}\right]$ is the expression of the coefficient matrix in front of the unknown parameters; each unknown parameter coefficient $\mathbf{\theta }$ is subject to approximate expansion method by wavelet multi-resolution analysis (WMRA) as in Eq. (9):

where, $\mathbf{\Xi }={\left[{\xi }_c^T,{\xi }_k^T,{\xi }_{\beta }^T,{\xi }_{\gamma }^T\right]}^T$ is wavelet expansion coefficient matrix, $\mathbf{W}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}[{\mathbf{w}}_c,\mathrm{}\mathrm{}{\mathbf{w}}_k,\mathrm{}\mathrm{}{\mathbf{w}}_{\beta },\mathrm{}\mathrm{}{\mathbf{w}}_{\gamma }]$ is reconstruction matrix of corresponding wavelet expansion. Substituting Eq. (9) into Eq. (8) gives:

where, $\mathbf{Q}=\mathbf{\Gamma }\mathbf{W}$ contains both the discretized responses $\mathrm{\Gamma }$and the sampled value $\mathbf{W}$ of wavelet function under various resolution levels. Eq. (10) shows that wavelet coefficient expansion $\mathbf{\Xi }$ can be obtained by linear least squares pseudo-inverse solution:

where, $(\cdot {)}^{+}$ represents Pseudo inverse, the parameters vector $\mathbf{\theta }$ can be obtained via the back substitution of $\mathbf{\Xi }$ into Eq. (9).

4.1. Nonlinear detection of isolation bearing

First, wavelet singularity detection is used to analyze the nonlinear state of isolation bearing. The harmonic excitation is $F=\mathrm{s}\mathrm{i}\mathrm{n}\left(2\pi ft\right)$, the sampling frequency is 1 Hz.

Fig. 1 shows the response of the acceleration in 5-10 s, and the response is decomposed by $db4$, $d1$ is used to extract the detail signal. Fig. 2 shows the extraction of d1 detail signal via the 10-layer wavelet multi-scale decomposition. Fig. 3 shows the variation law of instantaneous stiffness of the isolation bearing. Fig. 2 and 3 show that discontinuity points occur in detail signal while the instantaneous stiffness of isolation bearing abruptly change, which further verify that $d1$ can be adopted to characterize the variation when isolation bearing enters nonlinear under harmonic excitation. However, under seismic excitation, singularity analysis is not able to identify the nonlinear time-domain variation process of the isolation bearing, as the non-stationary characteristics of seismic excitation cover the nonlinear characteristics of the system.

Fig. 1Acceleration response under harmonic excitation

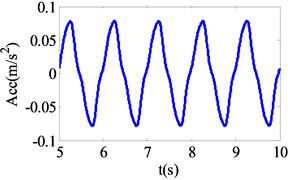
Fig. 2Detail signal d1

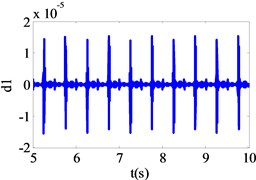
Fig. 3Instantaneous equivalent stiffness

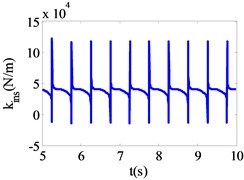
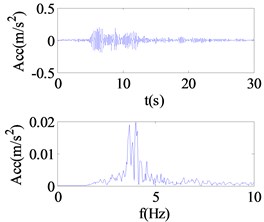
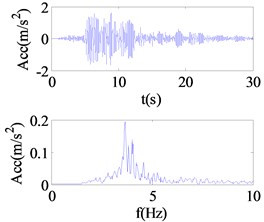
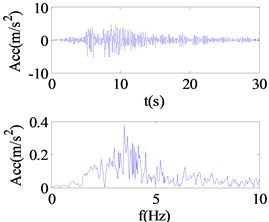
Fig. 4Responses and Fourier spectra under different seismic excitation levels

a)

b)

c)

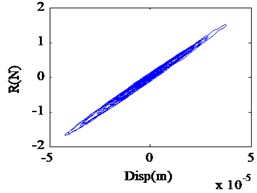
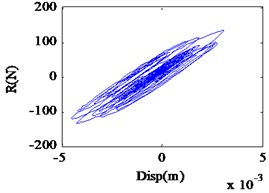
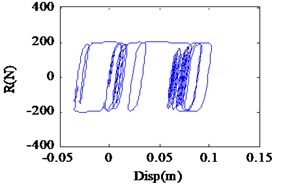
Fig. 5Restoring force curve under different seismic excitation levels

a)

b)

c)

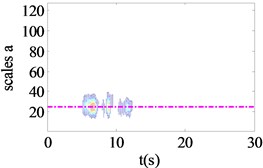
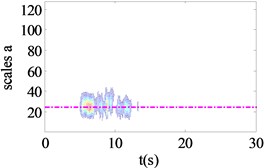
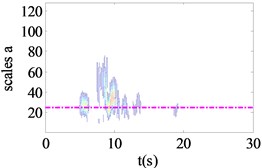
Fig. 6WCER expressed in time-scale

a)

b)

c)

In order to overcome the above constraints, wavelet coefficient energy ratio index proposed in the previous section was used to detect the nonlinear state of isolation bearing. Fig. 4(a)-(c) shows the Fourier spectra under different seismic excitation amplitude of 0.01 g, 0.1 g and 0.5 g respectively. Fig. 5(a)-(c) shows the restoring force curves of the corresponding seismic excitation amplitude; the isolation bearing is in the linear stage when the amplitude of seismic excitation is 0.05 g, with the increase of excitation intensity, the shape of the hysteresis loop is plumper, showing stronger nonlinearity. Fig. 6(a)-(c) shows the WCER expressed in time-scale under different seismic excitations. When isolation bearing is in linear, the energy is concentrated in the $t=$ 2-5 s time period and evenly fluctuates with in the baseline of the scale $a=$ 23. With the increase of the nonlinearity, the scale range of the energy distribution increases obviously, and the phenomenon of uneven distribution near the baseline of $a=$ 23 is occurred with the emergence of energy in the other time, as shown in Fig. 6(b), (c). Therefore, WCER can visually reveal the existence and state (strong/weak) of nonlinearity.

4.2. Nonlinear identification of isolation bearing

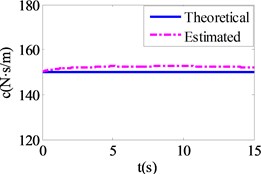
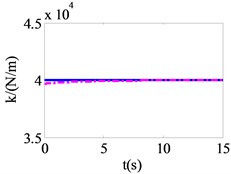
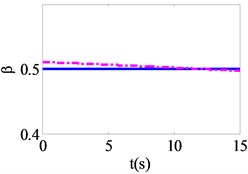
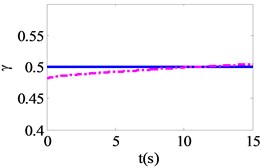
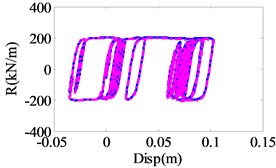
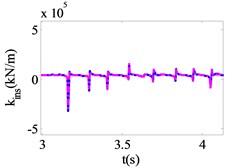
After detecting the nonlinear state of isolation bearing, the structure and model parameters are identified according to wavelet multi-resolution method in Section 3.2. The identification results are presented in Fig. 7 as solid curves. Also shown in Fig. 7 as dashed curves are the theoretical results for comparison. It is seen that the equivalent stiffness $k$ damping coefficient $c$ and model parameters $\beta$, $\gamma$ can be identified with good accuracy. Through a large number of numerical calculations, it is observed that the identification accuracy of the isolation bearing is proportional to its nonlinearity.

Fig. 7Identification results of isolation bearing

a)

b)

c)

d)

e)

f)

The nonlinear restoring force and the instantaneous stiffness of isolation bearing are calculated by the identified parameters results. The comparison results of the theoretical value and the identification value of the restoring force and instantaneous stiffness are plotted in Fig. 7(e), (f). Therefore, the abrupt change of instantaneous stiffness at these time points can be accurately identified.