Study on damage identification of earthquake damaged structures based on unsupervised learning method

1. Introduction

An 8-magnitude earthquake broke out in Wenchuan of Sichuan Province on 12 May 2008, and this earthquake caused destruction of numerous housing constructions and severe casualties. After this earthquake, most housing constructions underwent collapse and destruction. Moreover, in regions affected by the earthquake, housing constructions were damaged to varying degrees.

After the structure underwent load effect of sudden-onset disasters, it is quite necessary and significant for guaranteeing the soundness of engineering structure, preventing engineering disasters and safeguarding life and property safety of citizens to establish correct structural damage identification methods, determine the position and degree of structural damage, and formulate reinforcement treatment measures [1-3]. Damage identification of engineering structure has also become a hot issue in structural engineering researches in various countries [4-6]. It has strong engineering application background and significance to study structural damage identification problems.

2. Engineering overview

As a 6-floor production complex building, the communication complex building of a certain company was constructed in 2002, with a construction area of 4,828.57 m². Major structure of this complex building is frame structure; filling block and brick wall are adopted for the wall. During Wenchuan earthquake that happened on 12 May 2008, the major structure was affected. Therefore, a certain unit was entrusted to conduct safety detection and identification for it. In the same year, this unit was entrusted to carry out reinforcement design and reinforcement construction. Before structure reinforcement, no dynamic test was conducted for this structure, and dynamic characteristic parameters of this structure under damaged state before reinforcement are unknown. Therefore, dynamic characteristic parameters of the structure under original state (no structural damage) can be obtained only via intelligent information processing technology based on unsupervised learning method according to materials provided by Party A.

3. Finite element modeling and result analysis

3.1. Finite element model

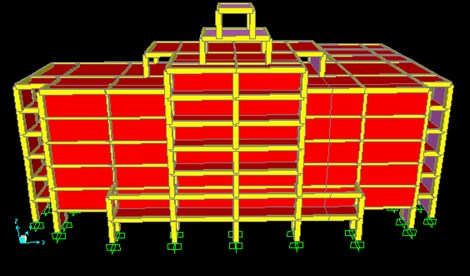
Finite element model of this frame is established via finite element software, as shown in Fig. 1.

Fig. 1Finite element model

3.2. Modal analysis of the structure

Natural vibration characteristics of the structure mainly include natural vibration period and vibration mode. Natural vibration frequency and vibration mode of the structure can be gained via modal analysis. See Table 1 for the results.

Table 1Natural vibration frequency of the structure (Hz)

Order	Natural vibration frequency of the frame structure
First-order translation at south-north direction	2.4455
First-order translation at east-west direction	2.5370
First-order torsion	3.5381
Second-order torsion	5.3221
Second-order translation at south-north direction	6.5616
Second-order translation at east-west direction	7.4598

Fig. 2Structural mode

a) First-order translation at south-north direction

b) First-order torsion

From dynamic characteristics of the structure, it can be seen easily that the results gained via modeling based on unsupervised learning method are almost consistent with data provided by Party A.

See the Fig. 2 for vibration mode of the structure in the extract.

4. Stiffness identification and calculation

For common masonry structure and frame structure with uniform stiffness distribution, vibration model of the structure can be simplified into multi-particle shear model during analysis. In another word, the stiffness matrix is tridiagonal linear type and the mass matrix is main-diagonal linear type. Each floor can be used as a concentrated mass put on the floor slab and story stiffness is treated as a spring model [7-10].

Structural motion equation of this model can be acquired according to structural vibration theory. In order to make it convenient to analyze the problem, the influence of structural damping will not be considered in this paper:

Characteristic equation of the system can be obtained:

where $\lambda ={\omega }^2$, and Eq. (2) is the generalized characteristic equation of the structure. This equation is corresponding to generalized eigenvalue issue in mathematics, which is Jacobi matrix in mathematics.

In practical engineering, physical parameters of the structure are actually identified according to two intrinsic frequencies (eigenvalues) and corresponding vibration modes (eigenvectors) measured in the vibration test. Frequencies ${\omega }_1$, ${\omega }_2$ and vibration modes ${\varphi }_1$, ${\varphi }_2$ of the previous two orders can be gained by measurement. By standardizing the vibration modes, the following matrix can be obtained:

The matrix is solved and $n$-order Jacobi matrix is finally determined. Jacobi matrix $J$ is obtained via analysis:

Stiffness and mass of the structure can be identified according to the recurrence relation:

(1) $a_1$, $b_2$, $m_1$, $m_2$ are given, and $k_1$, $k_2$ are calculated. The equation is:

(2) $k_1$, $k_2$ are given, and $k_3$, $m_3$ are calculated. The equation is:

(3) $a_{i-1}$, $b_{i-1}$, $k_{i-1}$, $m_{i-1}$ are given, and $k_i$, $m_i$ are calculated. The equation is:

(4) $a_n$, $b_{n-1}$, $k_{n-1}$, $m_{n-1}$ are given, and $k_n$, $m_n$ are calculated. The equation is:

In practical engineering, mass of various floors of the structure can be estimated by way of drawing or field measurement. Then mass matrix $M_n$ of the structure will be obtained. Thus stiffness of the structure can be calculated.

5. Detection scheme

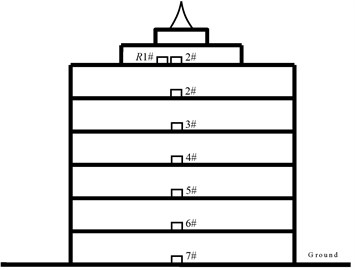
In this test, vibration picking was conducted via the acceleration sensors arranged in the mass centroid at various floors of the frame structure, amplifier was used for enlargement, and the acceleration signal was collected through the acquisition instrument. The sampling frequency is 40 Hz and the sampling time is 30 minutes. See Fig. 3 for the arrangement plan of sensors.

Fig. 3The arrangement plan of sensors

6. Test result analysis

Natural vibration frequency and vibration mode at various orders of this structure are gained via modal analysis for the actually measured acceleration signal. Stochastic subspace identification method is mainly adopted for modal analysis.

Fig. 4 is stability diagram of the structure at two directions gained via stochastic subspace identification method. The stability diagram is composed of two parts. The first part is cross spectrum or frequency-response function curve, and it is presented in the form of logarithmic equal altitude at the longitudinal direction, and the horizontal frequency is displayed in a linear way. At the vertical position corresponding to the spectrum peak, a row of characteristic frequencies should appear. In the second part, letters are used to signify features of characteristic frequency gained by the calculation model of different orders.

Fig. 4Stability diagram of the structure based on stochastic subspace identification method

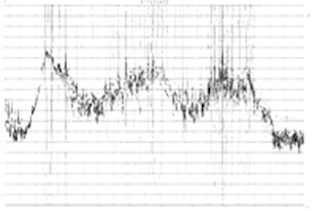
a) East-west direction

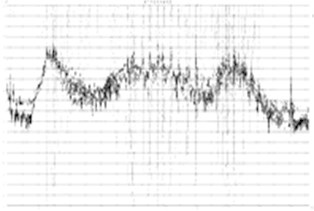
b) South-north direction

Fig. 5Correlation check matrix of vibration mode

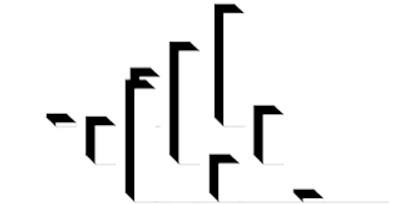
The reliability of vibration mode result in modal analysis can be checked by utilizing correlation matrix of vibration mode. Fig. 5 shows the correlation check matrix of vibration mode in test data analysis.

Modal analysis is conducted via measured data and natural vibration frequency of the structure at two directions is obtained, as shown in Table 2.

According to the comparison between dynamic characteristic parameters of the structure under original state in finite element modeling and the results after reinforcement in site test, first-order translation frequency of the structure is enhanced when compared with the original state and lateral stiffness of the structure after reinforcement is improved.

Stiffness values of the structure before and after reinforcement are obtained through calculation via MATLAB program written by our research group, as shown in Table 3. According to the analysis, horizontal stiffness at east-west direction of this frame structure is higher than the stiffness at south-north direction. Moreover, stiffness distribution at various floors is almost consistent with stiffness distribution rule of this structure. As per the data analysis, the increased stiffness value of the first floor and fourth floor is relatively small after reinforcement due to the great floor height of the first floor and large space layout of the fourth floor. Stiffness of other floors is increased greatly.

7. Conclusions

Before structure reinforcement, no dynamic test was conducted for this structure, and dynamic characteristic parameters of the structure are unknown. Therefore, any information about dynamic characteristic parameters of the structure under original state (the structure is not damaged in the earthquake on 12 May) can be obtained only via intelligent information processing technology based on unsupervised learning method according to materials provided by Party A. This method can gain dynamic characteristic parameters of the frame structure under original state and a comparison is made with results acquired in site test.

According to the analysis and comparison of test results, intelligent information processing technology based on unsupervised learning method is able to rapidly and conveniently obtain modal information of the structure during structural analysis. In this way, stiffness matrix of the structure can be identified by utilizing the inverse problem of eigenvalue. Its feasibility is proved via analysis. Besides, it is applied to practical reinforcement engineering and proves to have a good utility value in practical engineering.