A study of particles looseness in screening process of a linear vibrating screen

2.1. Introduction to DEM

It is an improvement that applying the Discrete Element Method (DEM) simulates and analyzes screening process of a linear vibrating screen [13]. The discrete element method that stems from the idea of molecular dynamics, is an explicit numerical method. It simulates the interactions of discrete particles including contact and collision in detail. Consequently, we can get certain information such as particle’s speed, location and so on. The fundamental theory of DEM is suitable for modeling of particle screening process. At a certain time, add up the contact forces acting on each particle, we can get the resultant force and resultant moment. According to Newton’s second law, we can get the following equation for the $i$th particle:

In the both equations, $X_i$ is the translational distance, $\sum F\left(t\right)$ is the resultant force and $m_i$ is mass of the $i$th particle. ${\theta }_i\text{,}$$\sum M\left(t\right)$ and $I_i$ are angular displacement, resultant moment and rotary inertia of the $i$th particle respectively.

2.1.1. 2.2 3D-DEM simulation

In this section, a 3D-DEM model was set up (Fig. 1) to simulate the movements of all particles in screening process. DEM model was proved that it has a good agreement between numerical simulation and experimental results [14].

Fig. 13D-DEM model of vibration screening

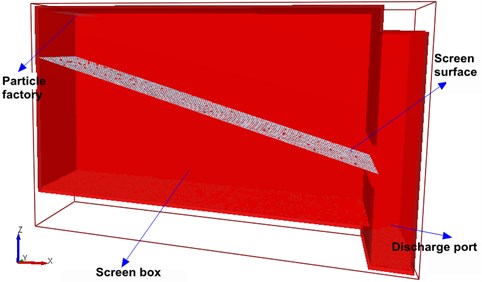
The model consists of screen box, screen surface and particle factory. The screen box is 162 mm in length, 32 mm in width and 80 mm in height. The screen mesh is combined with wire diameter is 0.7 mm and the aperture which is square with side length 1 mm. The particle factory provided the particles which are composed of different sizes. This paper employed a bimodal normal distribution of particles with the standard deviation which is 0.545. The particles consist of approximately spherical sands with mean diameters 0.5 mm and 1.0 mm respectively. The particles generated by the particle factory drop to screen surface under the action of gravity, and then particles will be rebounded when they touch screen surface. The average distances of particles which are rebounded over the screen surface are time-varying. The simulation conditions and parameters are listed in Table 1. There are three groups of parameters in case that each groups of experiment only changed one parameter value while others kept constant have been performed.

Table 1Summary of conditions

Material properties	Poisson’s ratio	Density	Shear modulus
Particles	0.3	2678 kg/m3	23 MPa
Screen	0.29	7861 kg/m3	79.92 GPa
Collision properties	Coefficient of restitutions	Coefficient of static friction	Coefficient of rolling friction
Particle-particle	0.1	0.545	0.01
Particle-screen	0.2	0.5	0.01
Particle generate rate 50000 particles/s	Screen declination 21°	Screen vibration Sinusoidal translation	Total number 30000
Text group Group one	Amplitude (mm) 1.5, 2.55, 3.55, 4.49, 5.7	Frequency (Hz) 20	Vibration angle (°) 100
Group two	2.55	10, 20, 30, 40, 50	100
Group three	2.55	20	30, 45, 51, 60, 70, 80

3.1. The movement of the screen surface

In order to study the particles rebounded over the screen surface, it is necessary to get the location of the screen surface. Screen surface was driven a sinusoidal translation in the direction of vibration (Fig. 2), the equation of displacement is given as following:

where $A$ is the amplitude moves along the vibrational direction, $\omega$ is the circular frequency, $t$ is the time, and $\phi$ is the phase angle. The displacement is compartmentalized into $S_x$ (perpendicular to the screen surface) and $S_y$ (parallel to the screen surface), given by:

where $\beta$ is the vibration direction angle (Fig. 2).

3.2. Definitions of the average distance, looseness coefficient and looseness rate

Because of particle-particle and particle-screen interactions over the screen surface, the average distance between two particles is diverse in different vibrational parameters over time. If the distance is too large or too small, the number of particles which penetrate aperture of screen will decrease. The material looseness is a main factor which affect the screening efficiency [15]. Fig. 2 shows a sketch about the side elevation and plan view of vibrating screen. Fig. 3 shows the projection of particles on the vibrating screen in EDEM software. The distance between particle 1 and particle 2 along the $X$ direction is $L_x$, as well as $L_y$ is the length in $Y$ direction. So the distance length, $L_1$, is given by:

Fig. 2The side elevation and plan view of vibrating screen

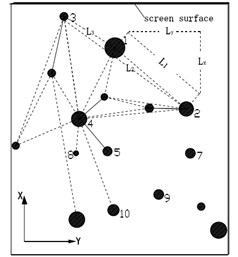
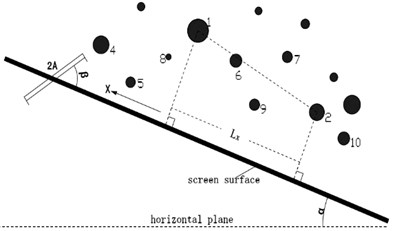
Fig. 3The side elevation and plan view of vibrating screen in EDEM

In this case, we assume that there are a total of $i$ particles rebounded over screen surface, and we can get $N$ lines by connecting any two particles’ centers. The average distance $L_A$ is expressed as follows:

In addition, in order to describe the looseness accurately, this paper defined a looseness coefficient. The looseness coefficient $C$ is given by:

where $D_A$ is the mean diameter of particles rebounded over screen surface. The looseness rate is the derivative of looseness coefficient with respect to time:

where $v_c$ is the looseness rate which indicates the tendency of particles being scattered reasonably, in other words, whether a favorable looseness or not; $\dot{C}$ the derivative of $C$ with respect to time.

3.3. Calculations and discussions

3.3.1. Looseness coefficient: change over time

During the simulation of the screening process, the particles which dropped from the particle factory took 0.3 s to move to the end of screen surface and took approximately 1.3 s to complete the whole screening. The period from 0.3 to 0.65 s was used to study the process of particles looseness because, in the meantime, particles flowed over the whole screen surface and the condition of particles looseness is an easy experimental phenomenon to observe. When particles were rebounded, the average distance between particles increased gradually and then remained stable. The period of looseness was divided into 0.3, 0.4, 0.5, 0.55, 0.6, and 0.65 s, in particles looseness process, the simulation data were used to obtain the change in looseness coefficient over time. A fitting function was given by:

11

$y=a+c{e}^{\frac{-(t-b)}{d}},$

where $t$ is time, in seconds; $y$ the looseness coefficient; and $a$, $b$, $c$, and $d$ change with the vibrational parameters. The fitting function curve of looseness coefficient to time is shown in Fig. 4. Those figures and curves showed that the looseness coefficient increases with the course of time and it has little change after about 0.65 s.

Fig. 4Looseness coefficient vs. time

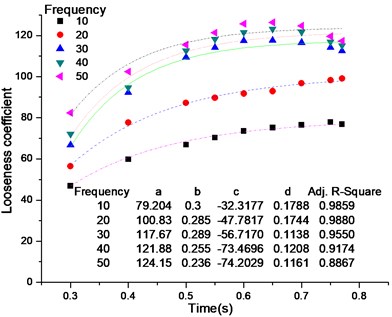
a) Looseness, parameterized by frequency

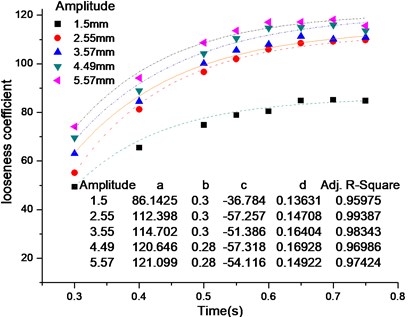
b) Looseness, parameterized by amplitude

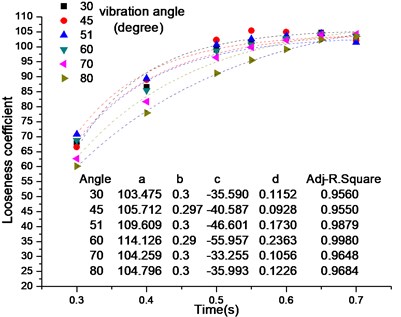
c) Looseness, parameterized by vibration direction angle

Only change one value of one parameter while other parameters keep constant. Fig. 4(a) and 4(b) show that the looseness coefficient increase with amplitude or frequency increase gradually. And the looseness coefficient is greater than 80, particles were sufficiently scattered. Amplitude impacts on the kinetic energy of the particles rebounded over screen surface and frequency mainly influences the bounce state of particles rebounded over screen surface. Large amplitude and high frequency were easy to make the particles full of the screen-box, and the particles were bounced higher and further easily. It indicates that particles have less chance to hit screen surface. Fig. 4(c) shows there is little effect on the energy of particles. The diversities in looseness coefficient is small in different vibration direction angles.

Table 2Mean values of looseness rate for different conditions

Frequency (Hz)	10	20	30	40	50
Mean $v_c$	74.3108	101.6911	137.1371	133.4182	104.9135
Amplitude (mm)	1.5	2.55	3.55	4.49	5.57
Mean $v_c$	92.172	133.165	121.953	119.6222	108.1037
Vibration angle (°)	30	45	51	60	70	80
Mean $v_c$	90.6347	112.0823	94.3309	105.6343	108.6569	111.2023

3.3.2. Looseness rate for different vibration parameters

During screening process, the actual rate of looseness is hard to calculate. According to Eq. (10), the looseness rate is obtained as the derivative of Eq. (11):

12

$v_c=\dot{y}=-\frac{c}{d}{e}^{\frac{-\left(t-b\right)}{d}}.$

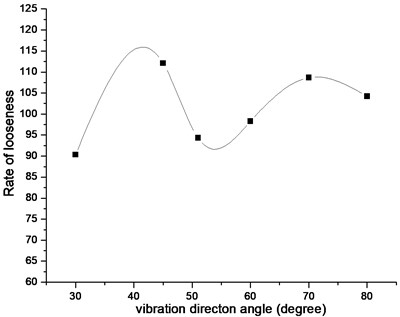
By using the mean, $v_c$, a statistical analysis between a looseness and a vibration parameter is given in Table 2. As well as the relationships among them were represented in Fig. 5, Fig. 6 and Fig. 7. In these figures, neither small values nor large values of parameters are beneficial to looseness. Fig. 5 and Fig. 6 depict that when amplitude is close to 2.7 mm and frequency approaches 34 Hz, the looseness rate reaches maximum. The reason accounts for those phenomena is that particles are fully scattered and reach stable state quickly. This two curves illustrate that the high frequency and large amplitude make particles obtain more energy to be active and the average distances get larger gradually. On the contrary, at low frequency and amplitude, the looseness coefficient and looseness rate are relatively low. In vibration direction simulation, two convex spots around 42 degrees and 70 degree depicted in the curve of Fig. 7. The degree of 42 produces the best performance.

Fig. 5Looseness rate vs. amplitude

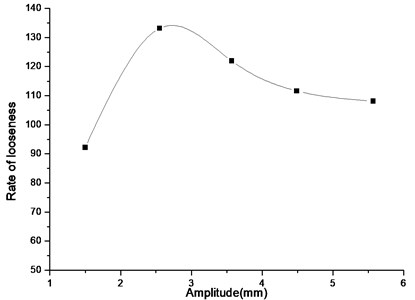
Fig. 6Looseness rate vs. frequency

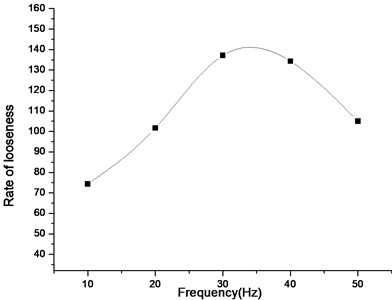
When the amplitude approaches 2.7 mm, the frequency is about 34 Hz and the vibration angle is around 42 degrees, the looseness ratio produces better performance. In order to improve screening efficiency of vibrating screen, we optimized the screening parameters which influence on screening efficiency in terms of particles looseness. In next part, physical experiments were used to verify the reliability of simulation results.

Fig. 7Looseness rate vs. vibration direction angle

4.1. Experimental setup

In this section, Sands (Fig. 8) were selected as raw materials. The shock type-based vibrating screen was used to separate different sized particles for matching the particle size distributions in simulation. The electric motor transmits power to the spindle through the drive plates. Then the worm gear located in the spindle drives the cam shaft, causing the vibration that drives the screen pedestal for both rotary and vibrating motions. Next, different sized particles were obtained through the screen meshing (Fig. 8).

Fig. 8Experimental particles with different size distributions

Fig. 9The particle movements are recorded by high-speed camera system and experimental prototype

Fig. 9 presents an experimental platform for tracking particles’ trajectory by using high-speed camera system and experimental prototype. Images of particles’ motions during the screening process were obtained and image quality was enhanced effectively. The means of the image processing including background elimination, image filter and binary processing. The combined and adjustable screen is an innovative design. Many screening parameters which under the influence of vibrational parameters can be conducted [2]. In this paper, the average distance and rate of looseness were carried out with different vibration frequency.

4.2. Experimental analysis and results

The purpose of these experiments is to obtain the relationship between two-dimensional image and three-dimensional information. From Fig. 10(a) three-dimensional information of calibration plate in world coordinate system by high-speed camera. Two-dimensional calibration plates’ images restore the three-dimensional information. By Matlab software the two-dimensional coordinates with image processing. Because of the large, complex and traditional calibration algorithm, this paper comes up with the camera calibration technique on account of neural network. The method is that the neuron conveys network information, network learning which decides network weights of neuron. The system sets up the mapping relationship between space point and image point in the range of allowable error. From Fig. 11, in the first image, the particles over the screening surface are shot. By image processing and BP neural network, three-dimensional coordinates were obtained.

Fig. 10Camera calibration process

a) Calibration plate shooting

b) Program processing of effective data points

Fig. 11Get particles coordinates

a) Grayscale image

b) Binary image

c) Coordinates of particles

4.3. Experimental results and comparison

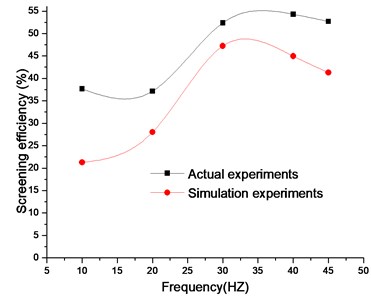
As numerical simulation mainly concerns collision properties, material properties, the size of vibrating screen and input quantity cannot match up with laboratory scale vibrating screen. There is a certain gap in the average distance among particles and rate of looseness between simulations and experiments. Cleary explores the critical influence of particle shape on granular system behavior [16-18]. Also, how to comprehensively and systematically describe the morphology of random particles reduces the gap. The average distance among particles is changed in different vibration frequency with time (Fig. 12). The same as Fig. 4(a), in some time the distance keeps stable. Meanwhile, when the frequency is about 30 Hz, the rate of looseness reaches the top as shown in Fig. 13. The screening efficiencies slightly differ (Fig. 14), however their screening principles are consistent. It indicates that we can understand the actual screening principle and looseness using numerical simulation.

Fig. 12Looseness distance under different frequencies with time

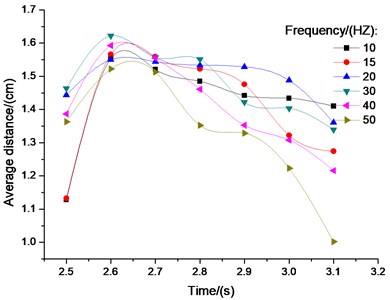
Fig. 13Average distance and looseness coefficient different frequencies with time

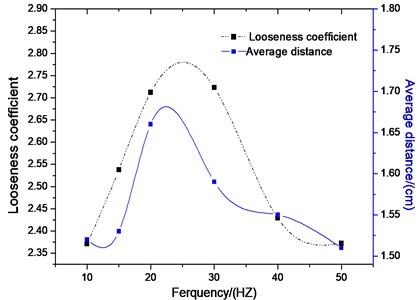
Fig. 14Comparison of experimental and simulation results