Vibration analysis of a single-layered graphene sheet embedded in visco-Pasternak’s medium using nonlocal elasticity theory

Zenkour, Ashraf M.

doi:10.21595/jve.2016.16585

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 June 2016

Check for updates

Vibration analysis of a single-layered graphene sheet embedded in visco-Pasternak’s medium using nonlocal elasticity theory

Ashraf M. Zenkour¹

¹Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah 21589, Saudi Arabia

¹Department of Mathematics, Faculty of Science, Kafrelsheikh University, Kafrelsheikh 33516, Egypt

Cite the article Download PDF

Downloads 1719

WoS Core Citations 15

CrossRef Citations 13

Abstract

The vibration analysis of a single-layered graphene sheet (SLGS) embedded in viscoelastic medium is presented by using the nonlocal elasticity theory. The medium is considered by adding the damping to the usual foundation model which characterized by the linear Winkler’s modulus and Pasternak’s (shear) foundation modulus. The governing dynamical equation is obtained and solved for simply-supported SLGSs. The effects of many parameters like nonlocal parameter, aspect ratio, Winkler-Pasternak’s foundation, damping coefficient, and mode numbers on the vibration frequencies of the SLGSs are investigated in detail. The present results are compared with the corresponding available in the literature. Additional results are tabulated and plotted for sensing the effect of all used parameters and to investigate the visco-Pasternak’s parameters for future comparisons.

1. Introduction

In recent years, the elements of nanostructures such as nanobeams, nanotubes and nanoplates are commonly used as components in nanoelectromechanical devices and other applications. Some of these nanostructured materials such as single-layered graphene sheets (SLGSs), multi-layered graphene sheets (MLGSs), fullerenes and different types of carbon nanotubes (CNTs) are fundamental building blocks of nanotechnology. Hence, accurate prediction of their thermo-mechanical behaviors becomes essential for engineering design and manufacture. But, controlled experiments on nanoscale are difficult to perform. The unique properties of the SLGSs or MLGSs make them very attractive in many scientific research aspects. Some remarkable mechanical properties of the GSs reveal that they have potential for creating novel ultrastrength composite materials [1, 2]. The GSs are mostly used in polymer composites as embedded structures to fortify them. Furthermore, the potential applications of the SLGSs as mass sensors and atomistic dust detectors have been investigated [3].

The notions of continuum mechanics have attracted a great deal of attention of many researchers to treat structures at the scale of nanometer. The classical continuum mechanics approaches are widely used but theory cannot predict the size effect. Successful applications of the classical continuum modeling to the vibration frequencies of CNTs and GSs have been reported by a number of research workers [4-12]. However, the classical continuum mechanics is scale independent which makes its applicability to the small-scale nanomaterials somewhat questionable. The size effects are recognized to become more pronounced as the dimensions of nanostructures become very small. It has been suggested that the nonlocal continuum theory presented by Eringen [13-16] should be integrated in the continuum models for accurate prediction of nanostructures mechanical behaviors [17]. The nonlocal Eringen’s theory is based on this assumption that the stress at a material point is considered as a function of the strain field at all material points in the continuum body. The inter-atomic forces and atomic length scales directly come to the constitutive relations as material parameters.

The extension of continuum mechanics to accommodate the size dependence of nanomaterials becomes another topic of major concern. Application of nonlocal continuum mechanics allowing for the small scale effects to vibration frequency analysis of nanomaterials has been also suggested by some other research workers in the study of nanostructures [18-43]. However, the inclusion of the damping effect as a third foundation parameter is rare in the literature. Arani et al. [44] have used the nonlocal elasticity theory to study the vibration analysis of the coupled system of DLGSs embedded in a visco-Pasternak foundation. Pouresmaeeli et al. [45] have studied the vibration characteristics of a simply-supported viscoelastic nanoplate using the nonlocal plate theory by including the effect of viscoelastic foundation. Mohammadi et al. [46] have studied the vibration behavior of circular and annular GSs embedded in a visco-Pasternak foundation and coupled with temperature change and under in-plane pre-load. Karličić et al. [47] have analyzed the free transverse vibration of a viscoelastic multi-nanoplate system embedded in a viscoelastic medium taking into account small-scale effects by using the nonlocal theory. Goodarzi et al. [48] have studied the free vibration behavior of rectangular graphene sheet under shear in-plane load. Hashemi et al. [49] have used the nonlocal theory to study the free transverse vibration of a nonlocal viscoelastic double graphene sheets coupled with visco-Pasternak layer. Zenkour [50] has presented the nonlocal transient thermal analysis of a SLGS embedded in viscoelastic medium.

The vibration frequency analysis of a SLGS embedded in a visco-Pasternak’s medium is presented to display various characters. The governing equation is obtained and solved analytically for a simply-supported SLGS. The effects of different parameters on the natural vibration frequencies are investigated. Sample results are tabulated and plotted for sensing the effect of all used parameters and to investigate the visco-Pasternak’s parameters for future comparisons.

2. Basic equation of single-layered graphene sheet (SLGS)

Let us consider a single-layered graphene sheet (SLGS) of length $a$ , width $b$ and uniform thickness $h$ as shown in Fig. 1. The SLGS is made of a homogeneous isotropic and linearly elastic material with Young’s modulus $E$ , Poisson’s ratio $ν$ , shear modulus $G$ and material density $ρ$ .

Fig. 1A continuum plate model of a single-layered graphene sheet embedded in a viscoelastic medium

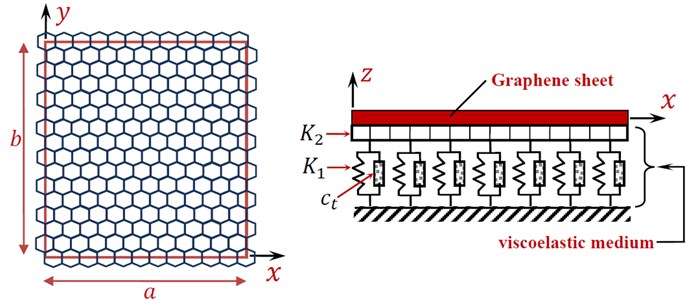
2.1. The visco-Winkler-Pasternak foundations

The two-parameter Pasternak’s model is the most natural extension to the one-parameter Winkler’s model. It considers a shear interaction between the spring elements by connecting the ends of the springs to a plate of an incompressible shear layer. The present SLGS is embedded in a homogeneous three-parameter viscoelastic medium. The foundation model is characterized by the linear Winkler’s modulus $K_{1}$ , the Pasternak’s (shear) foundation modulus $K_{2}$ , and the damping coefficient $c_{t}$ of the viscoelastic medium. Taking into account the un-bonded contact between the SLGS and medium, the interaction follows the three-parameter visco-Pasternak-type foundation model as:

1

R_{f} = (K_{1} - K_{2} a^{2} \nabla^{2} + c_{t} \frac{\partial}{\partial t}) w,

where $w$ is the transverse displacement and $\nabla^{2}$ is the Laplacian (second-order spatial gradient). Here, we have introduced the SLGS length $a$ in Eq. (1) for maintaining the dimension of $K_{1}$ and $K_{2}$ to be the same. If the foundation is modelled as the visco-Winkler foundation, the coefficient $K_{2}$ in Eq. (1) is zero. The viscosity term may be omitted by setting $c_{t} = 0$ to get the analysis of the SLGS embedded in pure elastic medium.

2.2. Nonlocal classical plate theory

The most general form of the constitutive relation in nonlocal elasticity theory involves an integral over the entire region of interest. The integral contains a nonlocal kernel function, which describes the relative influence of the strains at the various locations of the body on the stress at the material point under consideration. Specifically, the constitutive equation of nonlocal elasticity for homogenous and isotropic elastic solids read:

2

σ_{k l} (x) = \int_{V}^{} α (|x - x^{'}|) τ_{k l} (x^{'}) d V (x^{'}),

where $σ_{i j}$ is the nonlocal stress tensor, $V$ is the volume occupied by the elastic body, $|x - x^{'}|$ denotes distance in Euclidean space, and the nonlocal kernel $α (|x - x^{'}|)$ accounts for the effect of the strain at the point $x^{'}$ on the stress at the point $x$ in the elastic body.

The quantity $τ_{k l} (x^{'})$ denotes the local stress tensor for which the standard local constitutive equation is adopted, i.e.:

3

τ_{k l} (x^{'}) = λ ε_{m m} (x^{'}) δ_{k l} + 2 μ ε_{k l} (x^{'}),

where $ε_{k l} (x^{'})$ is the classical local strain tensor at $x^{'}$ , and $λ$ and $μ$ being Lamé’s constants.

The small strain-displacement relations are given by the usual relations:

4

ε_{k l} (x^{'}) = \frac{1}{2} (\frac{\partial u_{k} (x^{'})}{\partial x_{l}^{'}} + \frac{\partial u_{l} (x^{'})}{\partial x_{k}^{'}}),

where $u_{l} (x^{'})$ is the displacement vector at a reference point $x^{'}$ in the body. For an appropriate form of the nonlocal kernel [13-16], it turns out that the nonlocal internal constitutive relation given by Eq. (2) can be inverted to yield the following pseudo-local constitutive equation of gradient type:

5

[1 - {(l e_{0})}^{2} \nabla^{2}] σ_{k l} = τ_{k l} .

The parameter $l$ is an internal characteristic length (e.g., lattice parameter, granular distance), and $e_{0}$ is a material constant determined by experiment or by matching dispersion curves of plane waves with those of atomic lattice dynamics. One may see that when the internal characteristic length $l$ is neglected, i.e. the particles of the medium are considered to be continuously distributed and interacting without long-range forces, $l e_{0}$ is zero, and Eq. (5) reduces to the constitutive equation of classical local elasticity theory.

The displacement field models are chosen such that to ensure zero transverse shear stresses on top and bottom surfaces of the thicker plate. For the present very thin SLGS, it is sufficient and efficient to use the classical thin plate theory. The displacement field can be written as:

6

u_{1} (x, y, z) = u (x, y) - z \frac{\partial w}{\partial x}, u_{2} (x, y, z) = v (x, y) - z \frac{\partial w}{\partial y}, u_{3} (x, y, z) = w (x, y),

where $u_{1}$ , $u_{2}$ , and $u_{3}$ are the displacements in the $x$ , $y$ , and $z$ directions, $u$ , $v$ , and $w$ are the mid-plane displacements. Here $u$ and $v$ are the in-plane displacements while $w$ is the transverse displacement (deflection).

By substituting the displacement relations given in Eq. (6) into the strain-displacement equations of elasticity, the normal and shear strain components are obtained as:

7

\{\begin{matrix} ε_{x x} \\ ε_{y y} \\ γ_{x y} \end{matrix}\} = \{\begin{matrix} \frac{\partial u}{\partial x} \\ \frac{\partial v}{\partial y} \\ \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y} \end{matrix}\} - z \{\begin{matrix} \frac{\partial^{2} w}{\partial x^{2}} \\ \frac{\partial^{2} w}{\partial y^{2}} \\ 2 \frac{\partial^{2} w}{\partial x \partial y} \end{matrix}\}, ε_{z z} = γ_{y z} = γ_{x z} = 0 .

The corresponding stress-strain relationships in the isotropic SLGS coordinates can be expressed as:

8

\{\begin{matrix} σ_{x x} - ξ \nabla^{2} σ_{x x} \\ σ_{y y} - ξ \nabla^{2} σ_{y y} \\ τ_{x y} - ξ \nabla^{2} τ_{x y} \end{matrix}\} = \frac{E}{1 - ν^{2}} [\begin{matrix} 1 & ν & 0 \\ ν & 1 & 0 \\ 0 & 0 & \frac{1 - ν}{2} \end{matrix}] \{\begin{matrix} ε_{x x} \\ ε_{y y} \\ γ_{x y} \end{matrix}\},

where $ξ = {(l e_{0})}^{2}$ represents the nonlocal parameter.

2.3. Equation of motion

The governing equation of motion in the transverse deflection $w$ only can be obtained by using the dynamic version of the principle of virtual displacements in the form:

9

\frac{\partial^{2} M_{x x}}{\partial x^{2}} + 2 \frac{\partial^{2} M_{x y}}{\partial x \partial y} + \frac{\partial^{2} M_{y y}}{\partial y^{2}} + q - R_{f} = [I_{0} - I_{2} (\frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}})] \frac{\partial^{2} w}{\partial t^{2}},

where $M_{x x}$ , $M_{x y}$ , and $M_{y y}$ are the basic components of stress couples. They can be obtained by integrating Eq. (8) over the thickness of the plate as:

10

\{M_{x x}, M_{y y}, M_{x y}\} = \int_{- h / 2}^{h / 2} z \{σ_{x x}, σ_{y y}, τ_{x y}\} d z .

In addition, $I_{0}$ and $I_{2}$ represent the mass moments of inertia and are defined as:

11

\{I_{0}, I_{2}\} = \int_{- h / 2}^{h / 2} ρ \{1, z^{2}\} d z .

Using the stress-strain relationship, Eq. (8), and the stress resultants definition, Eq. (10), with the aid of Cauchy’s relations, Eq. (7), we can express stress resultants in terms of transverse displacement as follows:

12

\{\begin{matrix} M_{x x} - ξ \nabla^{2} M_{x x} \\ M_{y y} - ξ \nabla^{2} M_{y y} \\ M_{x y} - ξ \nabla^{2} M_{x y} \end{matrix}\} = - \frac{E h^{3}}{12 (1 - ν^{2})} [\begin{matrix} 1 & ν & 0 \\ ν & 1 & 0 \\ 0 & 0 & 1 - ν \end{matrix}] \{\begin{matrix} \frac{\partial^{2} w}{\partial x^{2}} \\ \frac{\partial^{2} w}{\partial y^{2}} \\ \frac{\partial^{2} w}{\partial x \partial y} \end{matrix}\} .

The substitution of Eq. (12) into Eq. (9) gives the following nonlocal governing partial differential equation in terms of transverse flexural displacement without the effect of the external load ( $q = 0$ ):

13

D \nabla^{4} w + (1 - ξ \nabla^{2}) [(K_{1} - K_{2} a^{2} \nabla^{2} + c_{t} \frac{\partial}{\partial t}) + (I_{0} - I_{2} \nabla^{2}) \frac{\partial^{2}}{\partial t^{2}}] w = 0,

where $D = E h^{3} / 12 (1 - ν^{2})$ is the flexural rigidity of the SLGS.

3. Solution of nonlocal vibration

The determination of natural frequencies is of fundamental importance in the design of many nano-structuers. The vibration formulation begins by assuming a solution of the displacement field. In particular, time harmonic waves are sought and it is assumed that the model is unbounded in $x$ and $y$ directions. Thus, the assumed form of the displacement is combinations of Fourier transform in $x$ and $y$ directions and Fourier transform in time $t$ :

14

w (x, y, t) = \sum_{m = 1, n = 1}^{\infty} W_{m n} \sin (λ_{m} x) \sin (μ_{n} y) e^{- i ω_{m n} t},

where $ω_{m n}$ is the circular frequency and $m$ , $n$ are the wavenumbers along $x$ and $y$ directions, respectively, $λ_{m} = m π / a$ , $μ_{n} = n π / b$ , and $i = \sqrt{- 1}$ .

To illustrate the preceding structural analysis, a variety of sample problems is considered. Whenever possible, comparisons are made with available solutions in the literature.

Substituting Eq. (14) into Eq. (13) we get:

15

A ω_{m n}^{2} + i B ω_{m n} + C = 0,

where:

16

A = [1 + ξ (λ_{m}^{2} + μ_{n}^{2})] [I_{0} + I_{2} (λ_{m}^{2} + μ_{n}^{2})], B = [1 + ξ (λ_{m}^{2} + μ_{n}^{2})] c_{t},

C = - D {(λ_{m}^{2} + μ_{n}^{2})}^{2} - [1 + ξ (λ_{m}^{2} + μ_{n}^{2})] [K_{1} + K_{2} a^{2} (λ_{m}^{2} + μ_{n}^{2})] .

Eq. (15) represents the frequency equation for the SLGS and its solution for $ω_{m n}$ is given by:

17

ω_{m n} = \frac{- i B \pm \sqrt{- B^{2} - 4 A C}}{2 A} .

4. Numerical results and discussions

It is to be noted that, we get the equation of vibrations of the SLGSs using local theory sheets by setting the value of $ξ = 0$ in Eq. (13). Correspondingly, the vibration frequencies of the local graphene are obtained. The fundamental frequencies for the present SLGSs are obtained with and without the inclusion of nonlocal parameter $ξ$ . In what follows we will use the following dimensionless variables:

18

ω = a \sqrt{\frac{ρ}{E}} ω_{m n}, k_{1} = \frac{a^{3} K_{1}}{D}, k_{2} = \frac{a^{3} K_{2}}{D},

where $k_{1}$ and $k_{2}$ are the foundation parameters.

For the sake of comparison, we will study the effect of nonlocal parameter. For this purpose, the frequency ratio (FR) is defined as:

19

F R = \frac{Frequency calculated using nonlocal theory}{Frequency calculated using local theory} = \frac{ω_{N L}}{ω_{L}} .

Properties of the graphene sheet in the validation analysis are considered in Table 1 [23]. The comparison of the results for vibration of nonlocal square SLGS between the present work and Refs. [23, 28, 29, 32] is presented in Table 2 with $a = b =$ 10 nm and $h =$ 0.34 nm and without the inclusion of visco-Pasternake medium. The present frequency ratio is the same as those presented in the literature. Now, let us consider some numerical examples to put into evidence the effect of the aspect ratio $a / b$ , the mode numbers $m$ and $n$ , the foundation parameters $k_{1}$ and $k_{2}$ , and the viscous damping coefficient $c_{t}$ on the vibration frequency of the present SLGS.

Table 1Properties of the graphene sheet

$E$ (TPa)	$ν$	$ρ$ (kg/m³)	$α$ 10^-6K^-1
1.06	0.25	2250	1.1

Table 2Comparison of the results for vibration of nonlocal square SLGS between the present work and Refs. [23, 28, 29, 32] (a=b= 10 nm and h= 0.34 nm)

$ξ$ (nm²)	$ω$ (GHz)	$ω_{N L} / ω_{L}$
$ξ$ (nm²)	$ω$ (GHz)	Present	[23]	[28]	[29]	[32]
0	0.19990	1	1	1	1	1
1	0.18268	0.91386	0.9139	0.9139	0.9139	0.9139
2	0.16926	0.84673	0.8467	0.8468	0.8466	0.8467
3	0.15843	0.79251	0.7925	0.7926	0.7926	0.7925

Benchmark results are presented in Table 3 for future comparison with other investigators. The effects of the nonlocal parameter $ξ$ , viscous damping coefficient $c_{t}$ , Winkler’s parameter $k_{1}$ , Pasternak’s parameter $k_{2}$ , and the mode number $n$ on the frequency $ω$ of SLGSs are discussed. Table 3 shows that the SLGS not embedded in visco-Pasternak’s medium gives the smallest frequencies $ω$ . The frequencies increase as the mode number $n$ increases and as the nonlocal parameter $ξ$ decreases. The SLGSs embedded in three-parameter (visco-Pasternak’s) medium give frequencies smaller than those of SLGSs embedded in two-parameter (Winkler-Pasternak’s) medium. For SLGSs embedded in three-parameter medium, the frequencies increase with the increase of the foundation parameters $k_{1}$ and $k_{2}$ and with the decrease of the viscous damping coefficient $c_{t}$ .

Additional plots are prepared in Figs. 2-6 by using the real value of the dimensionless frequency parameter $ω$ . The computations are carried out (except otherwise stated) for $m = 1$ , $a = 2 b$ , $b =$ 10 nm, $h =$ 0.34 nm, $k_{1} =$ 50 nN, $k_{2} =$ 10 nN, $ξ =$ 1 nm², and $c_{t} =$ 0.1 nN. Different values are given to the visco-Pasternak’s parameters $c_{t}$ , $k_{1}$ , and $k_{2}$ , and the aspect ratio $a / b$ of the SLGS. Here, we will discuss also the effect of the nonlocal parameter $ξ$ and the mode numbers $m$ and $n$ .

Fig. 2 plots the natural frequencies $ω$ vs the nonlocal parameter $ξ$ for different viscous damping coefficients $c_{t}$ , foundation parameters $k_{1}$ and $k_{2}$ , aspect ratios $a / b$ , and mode numbers $m$ and $n$ . The frequency increases with the increase of the foundation parameters $k_{1}$ and $k_{2}$ , aspect ratios $a / b$ and mode numbers $m$ and $n$ . However, the frequency decreases with the increase of the viscous damping coefficients $c_{t}$ . The variation of $ω$ is highly sensitive to the variation of all parameters.

Fig. 3 shows the variation of natural frequencies $ω$ vs the viscous damping coefficient $c_{t}$ for different nonlocal parameters $ξ$ , foundation parameters $k_{1}$ and $k_{2}$ , aspect ratios $a / b$ , and mode numbers $m$ and $n$ . Once again, the frequency increases with the increase of the foundation parameters $k_{1}$ and $k_{2}$ and mode numbers $m$ and $n$ . However, the frequency decreases as the nonlocal parameter $ξ$ increases. For lower values of $c_{t}$ , the frequency increases as $a / b$ increases while $ω$ decreases as $a / b$ increases for higher values of $c_{t}$ . In fact, the frequencies may be vanished for higher values of the viscous damping coefficient $c_{t}$ .

Table 3Natural frequencies ω (GHz) of nonlocal square SLGS (m= 1, a=b= 10 nm and h= 0.34 nm)

$ξ$	$c_{t}$	$k_{1}$	$k_{2}$	$n$
$ξ$	$c_{t}$	$k_{1}$	$k_{2}$	1	2	3	4	5
0	0	0	0	0.19990	0.49905	0.99574	1.68721	2.56964
0	0	50 100 200	10 20 30	0.54193 0.73987 0.92327	0.89714 1.16648 1.40272	1.43074 1.76139 2.05156	2.14334 2.51815 2.85287	3.03750 3.44235 3.81093
0	0.5	50 100 200	10 20 30	0.52068 0.72445 0.91095	0.88454 1.15682 1.39469	1.42294 1.75507 2.04613	2.13821 2.51379 2.84902	3.03395 3.43921 3.80810
0	1	50 100 200	10 20 30	0.45095 0.67608 0.87298	0.84560 1.12732 1.37033	1.39930 1.73595 2.02976	2.12275 2.50066 2.83744	3.02325 3.42978 3.79959
1	0	0	0	0.18268	0.40836	0.70640	1.03105	1.36074
1	0	50 100 200	10 20 30	0.53582 0.73541 0.91969	0.85004 1.13066 1.37307	1.24680 1.61555 1.92780	1.67638 2.13482 2.52096	2.11541 2.66426 3.12598
1	0.5	50 100 200	10 20 30	0.51431 0.71989 0.90733	0.83673 1.12068 1.36487	1.23785 1.60865 1.92202	1.66982 2.12967 2.51660	2.11030 2.66021 3.12253
1	1	50 100 200	10 20 30	0.44359 0.67119 0.86920	0.79546 1.09021 1.33997	1.21059 1.58777 1.90458	1.64998 2.11415 2.50348	2.09490 2.64801 3.11214
2	0	0	0	0.16926	0.35404	0.57741	0.80843	1.03768
2	0	50 100 200	10 20 30	0.53139 0.73219 0.91712	0.82532 1.11219 1.35791	1.17852 1.56346 1.88435	1.54944 2.03666 2.43839	1.92357 2.51465 2.99949
2	0.5	50 100 200	10 20 30	0.50970 0.71660 0.90473	0.81160 1.10205 1.34962	1.16904 1.55633 1.87844	1.54234 2.03126 2.43388	1.91795 2.51035 2.9959
2	1	50 100 200	10 20 30	0.43823 0.66766 0.86647	0.76898 1.07105 1.32442	1.14014 1.53474 1.86060	1.52084 2.01498 2.42031	1.90099 2.49742 2.98506
3	0	0	0	0.15843	0.31687	0.50032	0.68689	0.87128
3	0	50 100 200	10 20 30	0.52804 0.72976 0.91518	0.81007 1.10092 1.34870	1.14273 1.53666 1.86218	1.48964 1.99154 2.40083	1.83915 2.45067 2.94606
3	0.5	50 100 200	10 20 30	0.50620 0.71412 0.90276	0.79609 1.09068 1.34035	1.13295 1.52940 1.85620	1.48225 1.98602 2.39625	1.83327 2.44626 2.94239
3	1	50 100 200	10 20 30	0.43416 0.66500 0.86442	0.75259 1.05935 1.31498	1.10311 1.50743 1.83813	1.45986 1.96937 2.38247	1.81552 2.43299 2.93137

Fig. 2Natural frequencies ω vs the nonlocal parameter ξ

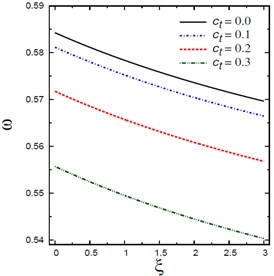
a) Damping coefficients $c_{t}$

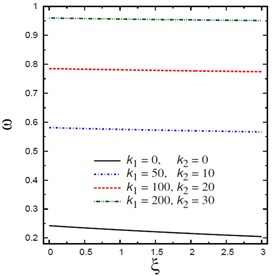
b) Foundation parameters $k_{1}$ and $k_{2}$

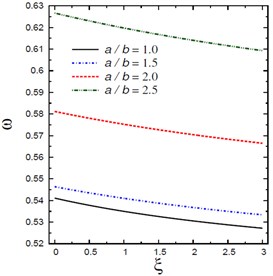
c) Aspect ratios $a / b$

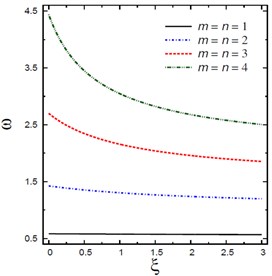
d) Mode numbers $m$ and $n$

Fig. 3Natural frequencies ω vs the damping coefficient ct

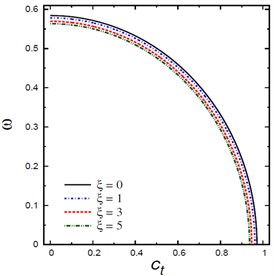
a) Nonlocal parameters $ξ$

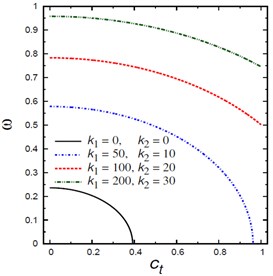
b) Foundation parameters $k_{1}$ and $k_{2}$

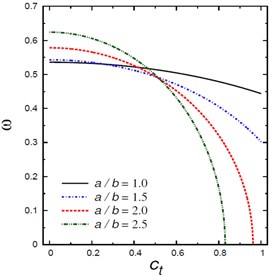
c) Aspect ratios $a / b$

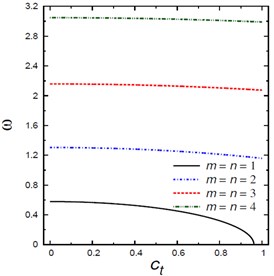
d) Mode numbers $m$ and $n$

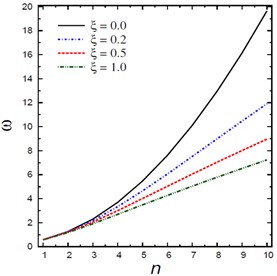
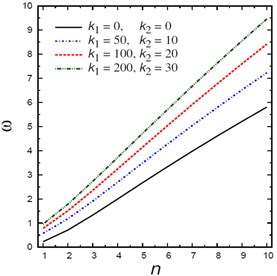
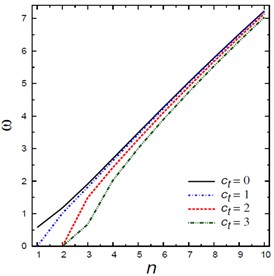
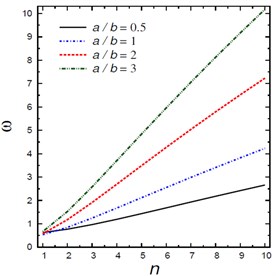
Fig. 4Natural frequencies ω vs the mode number n

a) Nonlocal parameters $ξ$

b) Foundation parameters $k_{1}$ and $k_{2}$

c) Damping coefficients $c_{t}$

d) Aspect ratios $a / b$

Fig. 5Natural frequencies ω vs Pasternak’s parameter k2

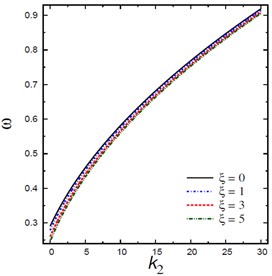
a) Nonlocal parameters $ξ$

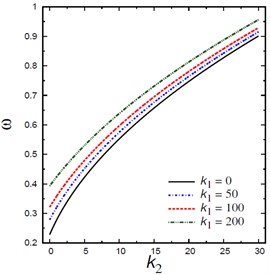
b) Winkler’s parameters $k_{1}$

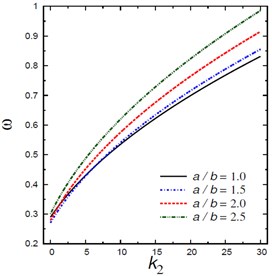
c) Aspect ratios $a / b$

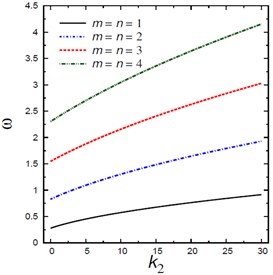
d) Mode numbers $m$ and $n$

Fig. 4 shows the natural frequencies $ω$ vs the mode number $n$ for different nonlocal parameters $ξ$ , foundation parameters $k_{1}$ and $k_{2}$ , damping coefficients $c_{t}$ , and aspect ratios $a / b$ . The frequency $ω$ increases as the mode number $n$ increases and this irrespective of the values of other parameters. The frequencies are increasing with the increase of the foundation parameters $k_{1}$ and $k_{2}$ and aspect ratio $a / b$ and are decreasing with the increase of the nonlocal parameter $ξ$ and damping coefficient $c_{t}$ .

Fig. 5 shows the natural frequencies $ω$ vs Pasternak’s parameter $k_{2}$ for different nonlocal parameters $ξ$ , Winkler’s parameters $k_{1}$ , aspect ratios $a / b$ , and mode numbers $m$ and $n$ . The frequency $ω$ increases as $k_{2}$ increases and this irrespective of the values of other parameters. The frequency is increasing with the increase of Winkler’s parameter $k_{1}$ , aspect ratio $a / b$ and mode numbers $m$ and $n$ while it is decreasing with the increase of the nonlocal parameter $ξ$ .

Finally, Fig. 6 plots the natural frequencies $ω$ vs the aspect ratio $a / b$ for different nonlocal parameters $ξ$ , foundation parameters $k_{1}$ and $k_{2}$ , damping coefficients $c_{t}$ , and mode numbers $m$ and $n$ . The frequency $ω$ is no longer decreasing as the aspect ratio $a / b$ increases and it has minimum values according to the values of other parameters. The frequencies are increasing with the increase of the foundation parameters $k_{1}$ and $k_{2}$ and mode numbers $m$ and $n$ and are decreasing with the increase of the nonlocal parameter $ξ$ and damping coefficient $c_{t}$ .

5. Conclusions

In this article, a single-layered graphene sheet is embedded in a three-parameter viscoelastic medium. The vibration frequency analysis is performed due to the nonlocal elasticity theory. For the sake of completeness and comparisons, some frequencies are tabulated here for different viscous damping coefficient, nonlocal parameter, aspect ratio, mode numbers, and Winkler-Pasternak’s elastic foundation. This article gives accurate frequencies as compared with the corresponding ones in the literature. The variation of frequency is highly sensitive to the variation of the different parameters. The maximum frequency occurs when the SLGS is embedded in two-parameter foundation medium without damping coefficient and with very low nonlocal parameter. In fact, the frequencies may be vanished for higher values of the viscous damping coefficient.

References

Stankovich S., Dikin D. A., Dommett G. H. B., Kohlhaas K. M., Zimney E. J., Stach E. A., et al. Graphene-based composite materials. Nature, Vol. 442, 2006, p. 282-286.

Publisher
Ramanathan T., Abdala A. A., Stankovich S., Dikin D. A., Herrera-Alonso M., Piner R. D., et al. Functionalized graphene sheets for polymer nanocomposites. Nature Nanotechnology, Vol. 3, 2008, p. 327-331.

Publisher
Sakhaee-Pour A., Ahmadian M. T., Vafai A. Applications of single-layered graphene sheets as mass sensors and atomistic dust detectors. Solid State Communications, Vol. 4, 2008, p. 168-172.

Publisher
Kitipornchai S., He X. Q., Liew K. M. Continuum model for the vibration of multilayered graphene sheets. Physical Review B, Vol. 72, 2005, p. 075443.

Publisher
Behfar K., Naghdabadi R. Nanoscale vibrational analysis of a multi-layered graphene sheet embedded in an elastic medium. Composites Science and Technology, Vol. 65, 2005, p. 1159-1164.

Publisher
Natsuki T., Endo M. Vibration analysis of embedded carbon nanotubes using wave propagation approach. Journal of Applied Physics, Vol. 99, 2006, p. 034311.

Publisher
Wang C. M., Tan V. B. C., Zhang Y. Y. Timoshenko beam model for vibration analysis of multi-walled carbon nanotubes. Journal of Sound and Vibration, Vol. 294, 2006, p. 1060-1072.

Publisher
Wang L., Ni Q. On vibration and instability of carbon nanotubes conveying fluid. Computational Materials Science, Vol. 43, 2008, p. 399-402.

Publisher
Wang L., Ni Q., Li M., Qian Q. The thermal effect on vibration and instability of carbon nanotubes conveying fluid. Physica E, Vol. 40, 2008, p. 3179-3182.

Publisher
Ansari R., Hemmatnezhad M. Nonlinear vibrations of embedded multiwalled carbon nanotubes using a variational approach. Mathematical and Computer Modelling, Vol. 53, 2011, p. 927-938.

Publisher
Ansari R., Hemmatnezhad M., Rezapour J. The thermal effect on nonlinear oscillations of carbon nanotubes with arbitrary boundary conditions. Current Applied Physics, Vol. 11, 2011, p. 692-697.

Publisher
Akgöz B., Civalek Ö. Free vibration analysis for single-layered graphene sheets in an elastic matrix via modified couple stress theory. Materials and Design, Vol. 42, 2012, p. 164-171.

Publisher
Eringen A. C., Edelen D. G. B. On nonlocal elasticity. International Journal of Engineering Science, Vol. 10, 1972, p. 233-248.

Publisher
Eringen A. C. Nonlocal polar elastic continua. International Journal of Engineering Science, Vol. 10, 1972, p. 1-16.

Publisher
Eringen A. C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. Journal of Applied Physics, Vol. 54, 1983, p. 4703-4710.

Publisher
Eringen A. C. Nonlocal Continuum Field Theories. Springer Verlag, New York, 2002.

Search CrossRef
Peddieson J., Buchanan G. R., McNitt R. P. Application of nonlocal continuum models to nanotechnology. International Journal of Engineering Science, Vol. 41, 2003, p. 305-312.

Publisher
Wang Q., Varadan V. K. Vibration of carbon nanotubes studied using nonlocal continuum mechanics. Smart Materials and Structures. Vol. 15, 2006, p. 659-666.

Publisher
Li R., Kardomateas G. A. Vibration characteristics of multiwalled carbon nanotubes embedded in elastic media by a nonlocal elastic shell model. Journal of Applied Mechanics, Vol. 74, 2007, p. 1087-1094.

Publisher
Xu K. Y., Aifantis E. C., Yan Y. H. Vibrations of double-walled carbon nanotubes with different boundary conditions between inner and outer tubes. Journal of Applied Mechanics, Vol. 75, 2008, p. 021013.

Publisher
Aydogdu M. Axial vibration of the nanorods with the nonlocal continuum rod model. Physica E, Vol. 41, 2009, p. 861-864.

Publisher
Pradhan S. C., Phadikar J. K. Small scale effect on vibration of embedded multilayered graphene sheets based on nonlocal continuum models. Physics Letters A, Vol. 373, 2009, p. 1062-1069.

Publisher
Pradhan S. C., Phadikar J. K. Nonlocal elasticity theory for vibration of nanoplates. Journal of Sound and Vibration, Vol. 325, 2009, p. 206-223.

Publisher
Murmu T., Pradhan S. C. Vibration analysis of nano-single-layered graphene sheets embedded in elastic medium based on nonlocal elasticity theory. Journal of Applied Physics, Vol. 105, 2009, p. 064319.

Publisher
Pradhan S. C., Murmu T. Small-scale effect on vibration analysis of single-walled carbon nanotubes embedded in an elastic medium using nonlocal elasticity theory. Journal of Applied Physics, Vol. 105, 2009, p. 124306.

Publisher
Arash B., Ansari R. Evaluation of nonlocal parameter in the vibrations of single-walled carbon nanotubes with initial strain. Physica E, Vol. 42, 2010, p. 2058-2064.

Publisher
Ansari R., Sahmani S., Arash B. Nonlocal plate model for free vibrations of single-layered graphene sheets. Physics Letters A, Vol. 375, 2010, p. 53-62.

Publisher
Pradhan S. C., Kumar A. Vibration analysis of orthotropic graphene sheets embedded in Pasternak elastic medium using nonlocal elasticity theory and differential quadrature method. Computational Materials Science, Vol. 50, 2010, p. 239-245.

Publisher
Pradhan S. C., Kumar A. Vibration analysis of orthotropic graphene sheets using nonlocal elasticity theory and differential quadrature method. Composite Structures, Vol. 93, 2011, p. 774-779.

Publisher
Ansari R., Arash B., Rouhi H. Vibration characteristics of embedded multi-layered graphene sheets with different boundary conditions via nonlocal elasticity. Composite Structures, Vol. 93, 2011, p. 2419-2429.

Publisher
Wang C. Y., Murmu T., Adhikari S., Mechanisms of nonlocal effect on the vibration of nanoplates. Applied Physics Letters, Vol. 98, 2011, p. 153101.

Publisher
Shen Z.-B., Tang H.-L., Li D.-K., Tang G.-J. Vibration of single-layered graphene sheet-based nanomechanical sensor via nonlocal Kirchhoff plate theory. Computational Materials Science, Vol. 61, 2012, p. 200-205.

Publisher
Natsuki T., Shi J.-X., Ni Q.-Q. Vibration analysis of circular double-layered graphene sheets. Journal of Applied Physics, Vol. 111, 2012, p. 044310.

Publisher
Zenkour A. M., Sobhy M. Nonlocal elasticity theory for thermal buckling of nanoplates lying on Winkler-Pasternak elastic substrate medium. Physica E, Vol. 53, 2013, p. 251-259.

Publisher
Zenkour A. M., Abouelregal A. E. Vibration of FG nanobeams induced by sinusoidal pulse-heating via a nonlocal thermoelastic model. Acta Mechanica, Vol. 225, 2014, p. 3409-3421.

Publisher
Mandal U., Pradhan S. C. Transverse vibration analysis of single-layered graphene sheet under magneto-thermal environment based on nonlocal plate theory. Journal of Applied Physics, Vol. 116, 2014, p. 164303.

Publisher
Zenkour A. M., Abouelregal A. E. The effect of two temperatures on a FG nanobeam induced by a sinusoidal pulse heating. Structural Engineering and Mechanics, Vol. 51, 2014, p. 199-214.

Publisher
Asemi S. R., Farajpour A. Thermo-electro-mechanical vibration of coupled piezoelectric nanoplate systems under non-uniform voltage distribution embedded in Pasternak elastic medium. Current Applied Physics, Vol. 14, 2014, p. 814-832.

Publisher
Zenkour A. M., Abouelregal A. E. Nonlocal thermoelastic nanobeam subjected to a sinusoidal pulse heating and temperature-dependent physical properties, Microsystem Technologies, Vol. 21, 2015, p. 1767-1776.

Publisher
Zhang Y., Lei Z. X., Zhang L. W., Liew K. M., Yu J. L. Nonlocal continuum model for vibration of single-layered graphene sheets based on the element-free kp-Ritz method. Engineering Analysis with Boundary Elements, Vol. 56, 2015, p. 90-97.

Publisher
Zenkour A. M., Abouelregal A. E., Alnefaie K. A., Zhang X., Aifantis E. C. Nonlocal thermoelasticity theory for thermal-shock nanobeams with temperature-dependent thermal conductivity. Journal of Thermal Stresses, Vol. 38, 2015, p. 1049-1067.

Publisher
Zenkour A. M., Abouelregal A. E., Alnefaie K. A., Aljinaidi A. A., Abu-Hamdeh N. H., Aifantis E. C. State space approach for the vibration of nanobeams based on the nonlocal thermoelasticity theory without energy dissipation. Journal of Mechanical Science and Technology, Vol. 29, 2015, p. 2921-2931.

Publisher
Karličić D., Cajic M., Kozić P., Pavlović I. Temperature effects on the vibration and stability behavior of multi-layered graphene sheets embedded in an elastic medium. Composite Structures, Vol. 131, 2015, p. 672-681.

Publisher
Arani A. G., Shiravand A., Rahi M., Kolahchi R. Nonlocal vibration of coupled DLGS systems embedded on visco-Pasternak foundation. Physica B, Vol. 407, 2012, p. 4123-4131.

Publisher
Pouresmaeeli S., Ghavanloo E., Fazelzadeh S. A. Vibration analysis of viscoelastic orthotropic nanoplates resting on viscoelastic medium. Composite Structures, Vol. 96, 2013, p. 405-410.

Publisher
Mohammadi M., Farajpour A., Goodarzi M., Mohammadi H. Temperature effect on vibration analysis of annular graphene sheet embedded on visco-Pasternak foundation. Journal of Solid Mechanics, Vol. 5, 2013, p. 305-323.

Search CrossRef
Karličić D., Kozić P., Pavlović R. Free transverse vibration of nonlocal viscoelastic orthotropic multi-nanoplate system (MNPS) embedded in a viscoelastic medium. Composite Structures, Vol. 115, 2014, p. 89-99.

Publisher
Goodarzi M., Mohammadi M., Farajpour A., Khooran M. Investigation of the effect of pre-stressed on vibration frequency of rectangular nanoplate based on a visco-Pasternak foundation. Journal of Solid Mechanics, Vol. 6, 2014, p. 98-121.

Search CrossRef
Hashemi Sh. H., Mehrabani H., Ahmadi-Savadkoohi A. Exact solution for free vibration of coupled double viscoelastic graphene sheets by visco-Pasternak medium. Composites Part B, Vol. 78, 2015, p. 377-383.

Publisher
Zenkour A. M. Nonlocal transient thermal analysis of a single-layered graphene sheet embedded in viscoelastic medium. Physica E, Vol. 79, 2016, p. 87-97.

Publisher

Cited by

New criteria for nanoscale slender beams and thin plates: Low frequency domain of flexural wave

Xiangyu Li | Chunfa Wang | Bo Zhang | Jianghong Yuan | Huaiping Tang

(2023)

Forced Flexural Vibrations due to Time-Harmonic Source in a Thin Nonlocal Rectangular Plate with Memory-Dependent Derivative

Iqbal Kaur | Kulvinder Singh

(2023)

Advances in Engineering Design

Harshad Patel | Saumil Desai | Mitesh B. Panchal

(2021)

A review of dynamic analyses of single- and multi-layered graphene sheets/nanoplates using various nonlocal continuum mechanics-based plate theories

Chih-Ping Wu | Hao-Xiang Hu

(2021)

Forced Flexural Vibrations in a Thin Nonlocal Rectangular Plate with Kirchhoff’s Thin Plate Theory

Iqbal Kaur | Parveen Lata | Kulvinder Singh

(2020)

Nonlocal electro-thermo-mechanical analysis of a sandwich nanoplate containing a Kelvin–Voigt viscoelastic nanoplate and two piezoelectric layers

Mohammad Arefi | Ashraf M. Zenkour

(2017)

Vibration and bending analysis of a sandwich microbeam with two integrated piezo-magnetic face-sheets

Mohammad Arefi | Ashraf M. Zenkour

(2017)

Size-dependent free vibration and dynamic analyses of piezo-electro-magnetic sandwich nanoplates resting on viscoelastic foundation

Mohammad Arefi | Ashraf M. Zenkour

(2017)

Nonlocal transient electrothermomechanical vibration and bending analysis of a functionally graded piezoelectric single-layered nanosheet rest on visco-Pasternak foundation

Ashraf M. Zenkour | Mohammad Arefi

(2017)

Thermo-electro-magneto-mechanical bending behavior of size-dependent sandwich piezomagnetic nanoplates

Mohammad Arefi | Ashraf M. Zenkour

(2017)

Employing sinusoidal shear deformation plate theory for transient analysis of three layers sandwich nanoplate integrated with piezo-magnetic face-sheets

Mohammad Arefi | Ashraf M Zenkour

(2016)

Buckling of a single-layered graphene sheet embedded in visco-Pasternak's medium via nonlocal first-order theory

Ashraf M. Zenkour

(2016)

TORSIONAL DYNAMIC RESPONSE OF A CARBON NANOTUBE EMBEDDED IN VISCO-PASTERNAK’S MEDIUM

Ashraf M. Zenkour

(2016)

About this article

Received

28 October 2015

Accepted

18 January 2016

Published

30 June 2016

SUBJECTS

Modal analysis

DOI

https://doi.org/10.21595/jve.2016.16585

Keywords

nonlocal elasticity theory

graphene sheet

vibration frequencies

visco-Pasternak’s medium

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2022 11 18

Vibration and instability of a fluid-conveying nanotube resting on elastic foundation subjected to a magnetic field

Ming Li, Junru Zhou, Qian Deng, Liufei Lv

Research article

2021 06 30

Vibration of a simply supported graphene sheet with uncertain small scale parameter based on nonlocal theory

G. Q. Xie, S. S. Ni

Research article

2016 12 31

Vibration and instability analysis of fluid-conveying nanotubes embedded in visco-elastic medium with consideration of surface effect

Ya-Xin Zhen

Research article

2016 05 15

Nonlinear free vibration analysis of nanobeams under magnetic field based on nonlocal elasticity theory

Tai-Ping Chang

A. M. Zenkour, “Vibration analysis of a single-layered graphene sheet embedded in visco-Pasternak’s medium using nonlocal elasticity theory,” Journal of Vibroengineering, Vol. 18, No. 4, pp. 2319–2330, Jun. 2016, https://doi.org/10.21595/jve.2016.16585

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2016.16585
UR  - https://doi.org/10.21595/jve.2016.16585
TI  - Vibration analysis of a single-layered graphene sheet embedded in visco-Pasternak’s medium using nonlocal elasticity theory
T2  - Journal of Vibroengineering
AU  - Zenkour, Ashraf M.
PY  - 2016
DA  - 2016/06/30
PB  - JVE International Ltd.
SP  - 2319-2330
IS  - 4
VL  - 18
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Zenkour_2016,
	doi = {10.21595/jve.2016.16585},
	url = {https://doi.org/10.21595/jve.2016.16585},
	year = 2016,
	month = {jun},
	publisher = {{JVE} International Ltd.},
	volume = {18},
	number = {4},
	pages = {2319--2330},
	author = {Ashraf M. Zenkour},
	title = {Vibration analysis of a single-layered graphene sheet embedded in visco-Pasternak's medium using nonlocal elasticity theory},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]A. M. Zenkour, “Vibration analysis of a single-layered graphene sheet embedded in visco-Pasternak’s medium using nonlocal elasticity theory,” Journal of Vibroengineering, vol. 18, no. 4, pp. 2319–2330, Jun. 2016, doi: 10.21595/jve.2016.16585.

Copy IEEE

Copied to clipboard!

Zenkour, Ashraf M. “Vibration Analysis of a Single-Layered Graphene Sheet Embedded in Visco-Pasternak’s Medium Using Nonlocal Elasticity Theory.” Journal of Vibroengineering 18, no. 4 (June 30, 2016): 2319–30. https://doi.org/10.21595/jve.2016.16585.

Copy Chicago

Copied to clipboard!

Vibration analysis of a single-layered graphene sheet embedded in visco-Pasternak’s medium using nonlocal elasticity theory

Abstract

1. Introduction

2. Basic equation of single-layered graphene sheet (SLGS)

2.1. The visco-Winkler-Pasternak foundations

2.2. Nonlocal classical plate theory

2.3. Equation of motion

3. Solution of nonlocal vibration

4. Numerical results and discussions

5. Conclusions

References

Cited by

About this article

Related Articles