Numerical investigation on flow-induced structural vibration and noise in centrifugal pump

2.1. Governing equations

Fluid flow inside a centrifugal pump is generally considered as complex three-dimensional turbulent flow. In this paper, the flow field inside the pump was solved by using large eddy simulation (LES) to catch the detailed characteristics of the unsteady flow. In LES, the three-dimensional time dependent large-scale turbulent motion was resolved directly and the effect of the unresolved (or subgrid) scales was taken into account by appropriate subgrid-scale (SGS) models [16]. The governing equations describing the behavior of the large scales are as following:

where the over bars indicate the spatial filtering. $\rho$ is fluid density, and $u$, $p$ and $\mu$ are velocity, pressure and viscosity of the fluid respectively. $t$ and $x$ are time and space coordinate, ${\tau }_{ij}$ is the sub-scale stress modeling. The subscript $i$ and $j$ are the direction component of coordinate. The unsteady flow fields were simulated with the commercial code Fluent. Bounded central differencing method was used to solve Eq. (1). For the discretization in the time domain, the second-order implicit format was adopted. The pressure-velocity coupling was calculated by means of the SIMPLEC algorithm. Second-order format was used for pressure term. Prior to the unsteady flow calculations, steady simulations were carried out by using a so-called multiple reference frame model. When achieving convergence, the results of which were used as initial condition to unsteady flow simulations. For the unsteady calculation, 60 time steps were considered per blade-passing period with a time step of 5.74e-5 s, namely the time impeller rotated through one degree. For each time step, the convergence criterion was established in a value of 1e-5 for the scaled residuals, with at least 50 iterations per time step. The unsteady simulations were considered when the flow reached a clear periodic regime, with a minimum of 5 full impeller revolutions.

2.2. Computational domain and meshing

Fig. 1 shows some views of the pump numerical geometry domain that is composed of inlet duct, impeller, volute and outlet duct. Straight ducts at inlet and outlet are used to prevent boundary condition effects on simulation of the pump flow domain. Fig. 2 shows surface meshes including a general view of the pump with the inlet duct, impeller and volute and a detail of the volute tongue and boundary layer of blade surface. The mesh is hexahedral elements with a total number of about 7,920,000 cells.

2.3. Boundary conditions

The boundary conditions imposed were a constant total pressure at the inlet, and the spectral synthesizer, which based on the random flow generation technique originally proposed by Kraichnan [17] and modified by Smirnov et al. [18], was used to generate fluctuating velocity components. This boundary condition avoids the definition of a fixed velocity profile in inlet suction. Flow rate boundary condition at the outlet and the no-slip conditions over wall. The relative motion of the impeller module with respect to the pump was taken into account by means of the sliding mesh technique at the impeller-volute and impeller-inlet duct grid interfaces.

Fig. 13D models of total domain including: (i) inlet duct, (ii) impeller, (iii) volute and (iv) outlet duct

Fig. 2Computational mesh for the investigated pump

a) Surface meshes of inlet duct and impeller

b) Surface meshes of volute

2.4. Numerical sensitivity analysis

In the numerical resolution of the flow equations, the precision of the results as well as the required computation resources are strongly affected by several numerical parameters [19] including the grid size, the time step, sampling time and the turbulence model etc. Before imposing the definitive vibration exciting source, a sensitivity analysis was done by comparing their effects on the pressure pulsation amplitude at some measuring points in the volute wall region, whose positions were illustrated in Fig. 3.

Fig. 4 illustrates the pressure fluctuation amplitude of BPF (290 Hz) at sampled points 1-6 with different near-wall grid sizes corresponding to nominal flow condition, where the first layer grid height of near-wall $h$ was normalized by viscous sublayer thickness ($\delta =34.2D_1/R{e}^{0.875}\approx$0.046 mm) flows in the inlet duct when Reyonds number is 3.6e5. Pressure fluctuation amplitude was normalized by using the circumferential dynamic pressure at the impeller exit diameter, i.e. $Cp=p_A/0.5\rho u_2^2$. It can be seen that the pressure pulsation amplitude of that point located at near the volute tongue strongly depends on near-wall grid size. And the amplitudes of BPF with respect to point 1 are shown as Table 2 with different near-wall grid sizes, from which it can be seen that it is reasonable to imposing accurate vibration exciting source if non-dimensional near-wall grid size $h/\delta <$0.26.

Fig. 5 presents typical spectrums of the pressure pulsation that was sampled at point 1 with different sampling times, where $T$ is the time that impeller rotates through 360 degrees. The spectrum was obtained by a Fourier transform; from which it can be seen that the amplitude of BPF is less affected by sampling time. But it is noticed that those amplitudes of the other frequency especially low frequency pulsation are more dependent on sampling time. The shorter the sampling time, the lower frequency resolution, give rise to aliasing errors, which can amplify the amplitude of some low frequency pulsation. With the increase of sampling time, the amplitude of the low frequency pulsation is gradually decreased. So it is reasonable to capturing pressure fluctuation amplitude if sampling time is greater than 7 full impeller revolutions.

Fig. 3Positions of the measurement points in the volute surface

Fig. 4The pressure fluctuation amplitude of BPF at different monitoring points

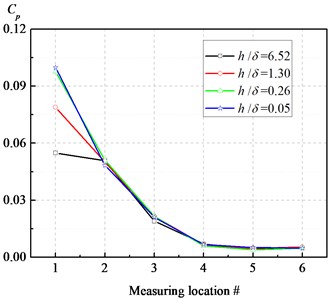
Fig. 5The spectrums of the pressure pulsation at point 1

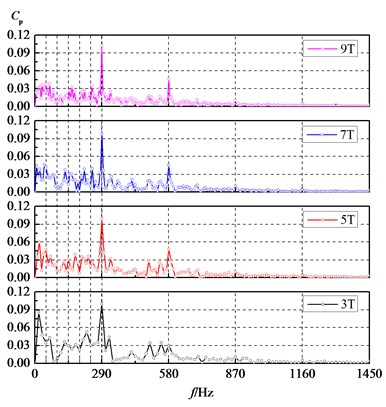
Fig. 6The spectrums of the pressure pulsation

2.5. Pressure fluctuations

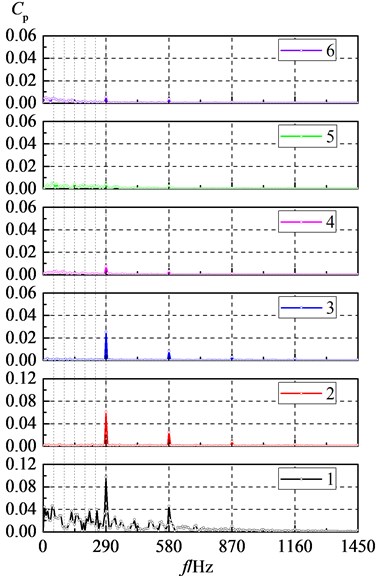
Fig. 6 shows spectrums of the pressure pulsation that was sampled at points 1-6. The spectrum was obtained by a Fourier transform, from which it can be seen that the pressure pulsation is dominated by the BPF (290 Hz) and its harmonic components and gradually decreasing along the spiral volute, which indicates the interaction, between the impeller and volute, is major contributors to pressure fluctuations in the centrifugal pump. It is noticed that pressure fluctuation of shaft frequency is quite prominent near the volute tongue, whose amplitude is about 41 % of that of BPF, which is consistent with the observed phenomenon in experimental results [20]. But to other monitoring points, the pressure fluctuation amplitude of shaft frequency is insignificant, which is different from experimental results [20]. This discrepancy may be because of the unbalanced motion of the rotor enhancing the pressure fluctuations of the shaft frequency in experimental process, but being neglected in numerical simulation.

3.1. Acoustic model

The governing equation for sound fields radiated by the volute vibration is Helmholtz equation:

where $p$ is the amplitude of the sound pressure fluctuation, $k=\omega /c$ is called the wavenumber. $\omega$ is the angular frequency and $c$ is the sound speed of the fluid.

In this study, Eq. (2) is solved by using boundary element method, which has been widely used in acoustics for computing the noise radiated from vibrating objects. For interior acoustic problem, boundary integral formulation equations with respect to Eq. (2) are shown as follows:

where $p\left({\overrightarrow{r}}_a\right)$ and $v_n\left({\overrightarrow{r}}_a\right)$ denote the sound pressure and normal velocity distribution on the close boundary surface $S$ respectively, and ${\rho }_0$ is mean fluid density. The symbol $G$ denotes the Green kernel function, which represents the free-field pressure in point $\overrightarrow{r}$ due to a unit acoustic point source excitation in ${\overrightarrow{r}}_a$:

The leading coefficient $C\left(\overrightarrow{r}\right)$ in integral Eq. (3) is 1 for $\overrightarrow{r}$ in the domain, 0 for $\overrightarrow{r}$ in the exterior domain and, 1/2 for $\overrightarrow{r}$ on a smooth boundary.

For numerical computation, the Helmholtz integral Eq. (3) is evaluated for each node $i$ on the boundary surface, which gives the following discretized equation:

where $\mathbf{A}$ and $\mathbf{B}$ are global coefficient matrix. For each collocation node$\mathrm{b}$, i.e. $\overrightarrow{r}={\overrightarrow{r}}_b$, this yields:

where ${\delta }_{bi}$ is the kronecker delta function and, $N_i$ is the shape function.

To use direct boundary element method, the inlet and outlet are blocked with elements, the non-reflecting condition is used in the simulation. According to linear time-harmonic acoustic simulation rule, six linear elements per wavelength is required. For our volute BEM acoustic model, the maximum valid frequency is 8700 Hz. So the mesh is sufficiently fine for the BPF (290 Hz) harmonic acoustic analysis.

3.2. Vibration model

The finite element model for vibrations of structure takes the form:

where $\left\{u_i\right\}$ is a displacement vector, $\left[\mathbf{K}\right]$, $\left[\mathbf{C}\right]$, $\left[\mathbf{M}\right]$ denote stiffness, damping and mass matrices of the structure respectively. $\left[{\mathbf{L}}_c\right]\left\{p_i\right\}$ is the force loading of the acoustic pressure on the structure along the fluid-structure coupling interface. The symbol ${\mathbf{L}}_c$ represents fluid-structural coupling matrix which is given by:

where $m$ is the number of coupling surface elements. $N_s$ and $N_a$ are the structure mesh shape function and acoustic mesh shape function, respectively. The symbol $n^e$ is the unit normal vector. $\left\{F_s\right\}$ is the external flow excitation force load, applied normal to the fluid-structure interface, the expression of which is:

For coupled vibro-acoustic problems, the discretized boundary integrated Eq. (5) and finite element Eq. (7) must be solved by simultaneously to including the mutual coupling interaction between the acoustic pressure and the structural vibration. And at the fluid-structure interface, the fluid normal velocity values $V_{ni}$ at the nodes of the acoustic mesh to the displacement components $u_i$ at the nodes of the structure mesh yield:

where $\left[\mathbf{T}\right]$ is the transformation matrix.

Fig. 7 shows a full scale structure mesh, which has 0.58 million 4-noded tetrahedral elements. Different types of element and dimensions are applied for different parts in order to get the fined geometry features. The coefficients used are: Modulus of elasticity $E=$210 GPa, density $\rho =$ 7850 Kg/m³, Poisson ratio $\sigma =$0.3.

Fig. 7Mesh used in structural simulation

3.3. Numerical results

A full scale centrifugal pump structural vibration and noise induced by flow was simulated by LMS Virtual Lab software. Structural models, as shown in Fig. 8, are mainly composed of inlet and outlet flanges, volute, shaft and motor etc. The springs with the different stiffness coefficients are adopted to simulate the two components connections in centrifugal pump. Moreover, prior to coupled vibro-acoustic systems were solved, the analysis of vibrating modal of the centrifugal pump components was carried out. For validating the computed modal, the comparisons between the computed free modal models of pump components for first natural frequency and experimental results, provided by Shanghai Marine Equipment Research Institute, were performed, and they agreed well as shown in Table 3. Then, the constrained modes of the centrifugal pump which connected with the inlet/outlet pipe were calculated and fifty-order models were also imported into the acoustic solver. The former tenth-order modes of the volute were shown in Table 4.

Fig. 9 shows spectrums of the vibration velocity that was sampled at the points a-c shown in Fig. 8, from which it can be seen that the structural vibration is dominated by the BPF components and with smaller peaks appearing at the third shaft frequency, the second and third blade-passing frequencies, which is in according with frequency spectral characteristics of pressure fluctuation. The BPF vibrations arise from rotor-stator interactions. From Table 4, it can be seen that the forth-order mode frequency of pump is close to the BPF of pressure fluctuation, so it is concluded that resonance maybe occur at this frequency. The amplitude of vibration velocity gradually increases from inlet (point a) to output (point b) then to volute tongue (point c), which indicates that the interaction between impeller and volute tongue can be the major contributor to the vibration and noise generation within the volute of a centrifugal pump. Moreover, the BPF vibration characteristics are coincident with the experimental results [21], although discrepancies do exist at the low frequency components and the shaft frequency, which may be caused by the unbalance of the rotor is neglected and only the dynamic surface pressure on the walls is used in simulation.

Fig. 8The centrifugal pump structure model

Fig. 9The spectrums of vibration velocity at points a-c

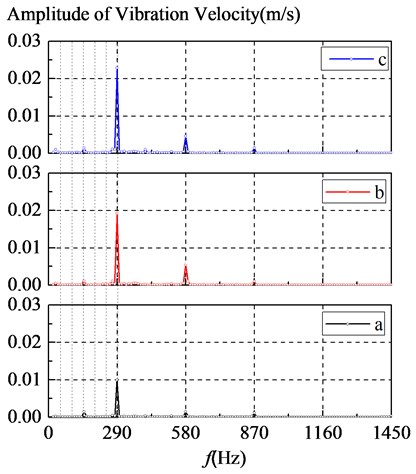
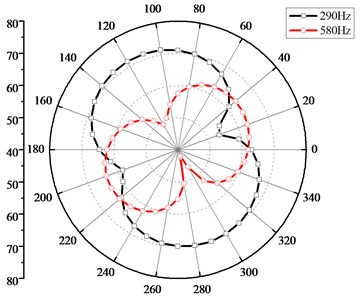
Fig. 10 illustrates thirty-sixth sound pressure monitors located at one meter away from the center of the pump and directivity distribution of outer radiation sound field induced by volute vibration corresponding to BPF and the second BPF respectively, from which it can be seen that directivity distribution of radiation acoustic field is typical dipoles. This is conforming to the fact that only the dynamic surface pressure (dipole source) is loaded and the monopole and quadrupole contributions of fluid-acoustic sources are neglected in the coupled simulation. The sound pressure level of radiation noise field excited by vibration is about 53-71 dB for BPF components and 42-63 dB for the second BPF respectively.

Fig. 10Monitoring points position and directivity distribution of radiation noise field