An analytical model for flutter behavior of composite panels with shape memory alloy fibers

1. Introduction

The surface panel of the vehicles made of lightweight composite may result in flutter or self-exited oscillation during high-speed flight. Although panel flutter does not indicate structural failure as happened in the aircraft wing, this may cause fatigue of panel and affect its aerodynamic characteristics, leading to poor flight performance. In the recent years, the studies of the flutter suppression using shape memory alloy materials have received much attention. It is only natural that SMA is embedded into the composite panel to increase the aeroelastic stability of vehicles. This is because composite panel is thin thanks to their high stiffness/weight ratio. On the other hand, SMA has a unique ability known as shape memory effect which can result in the large tensile recovery stress if the SMA is restrained. Large in-plane forces can be induced in the composite panel at temperatures higher than the austenite start temperature which increase the composite panel stiffness.

Weisshaar et al. [1-2] showed that the flutter boundary of the panel with partial SMA layer is significantly increased. Park et al. [3] and Duan et al. [4] investigated the control of the thermal post-buckling deflection, critical temperature and critical dynamic pressure by using the SMA. Ostachowicz et al. [5] studied the effect of SMA fiber on the flutter of the composite plate with delaminations. Recently, Kuo et al. [6] presented a study of the influence of SMA on the flutter of buckled composite laminates by varying the SMA fiber spacing.

However, most of the previous studies were performed based on finite element modeling of structures [3-6]. It can be seen that few researches presented analytical solutions [1-2] for flutter analysis of the composite panels with SMA. Furthermore, it is found that the thermo-mechanical behavior was described by the expression of approximate fitting or use of the approximate data obtained from the curves of SMA [3-4, 6]. And some important factors affecting the flutter behaviour of the composite panels with SMA have not studied enough and the time domain response was not provided.

In this work, an analytical solution is presented to investigate the effects of SMA fibers on the flutter behavior of composite panels. The thermo-mechanical constitutive equation of SMA proposed by Brinson [7] and the mixture rule for evaluating the elastic properties of a SMA hybrid composite layer [8] are employed to derive the constitutive equation of the SMA reinforced composite panels. The composite panels model uses laminated plate theory. The Galerkin approach is carried out to reduce the motion equations of composite panels with SMA fibers to a system of ordinary differential equations. Based on these approximate equations the flutter behavior of the composite panels are then calculated in the frequency and time domains. Finally, the influence of parameters including SMA activation on flutter behavior of the composite panels is examined.

2. Formulations

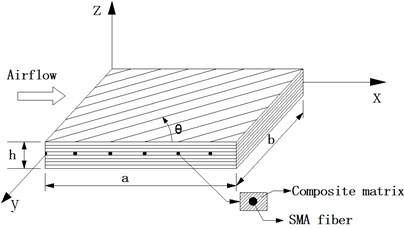
As shown in Fig. 1, a composite panel with length $a$, width $b$ and thickness $h$ is considered. The SMA fibers are embedded parallel to the fibers of composite medium in the arbitrary layers. Supersonic airflow with air density ${\rho }_a$, flow velocity $U_a$, Mach number $M$ is imposed on the composite panel. We assume that aerodynamic pressure $∆P$ is passing over the top surface of the composite panel along the $x$-axis.

Fig. 1Geometry of a composite panel embedded with SMA fibers.

The aerodynamic pressure obtained from quasi-steady supersonic aerodynamic theory has the form:

where $w$ is the transverse displacement component in the mid-plane of the composite panel.

The effect of the $\partial w/\partial t$ term, which causes aerodynamic damping, on the flutter boundary is insignificant [9] and is not included in this work.

By using the laminated plate theory and the one-dimensional model of SMA proposed by Brinson [7], the equation of motion for the composite panels with SMA fibers can be written as:

where $m_0$ is the panel mass per unit area, the panel bending stiffnesses $D_{ij}$ are defined as:

where ${\stackrel{-}{Q}}_{ij}$ is the transformed stiffness matrix of the layer, and:

in which:

where $m$ and $n$ are the cosine and sine functions of the ply angle in each lamina, respectively, and the stiffness matrix $Q$ has following form:

where:

The modulus and Poisson’s ratio of the composite panel can be determined by considering the mixture rule of composition [8]:

where, the subscript $\mathrm{m}$ and $\mathrm{s}$ denote the composite matrix and SMA fibers, respectively, $V$ is volume fraction.

$N_x$, $N_y$ and $N_{xy}$ in Eq. (2) are the resultant in-plane forces induced by SMA fibers and temperature, which can be given as:

where the superscripts ‘$r$’ and ‘$∆T$’denote the in-plane stresses induced by recovery stresses of SMA fibers and temperature, respectively.

The recovery stresses of SMA fibers and the stresses induced by temperature of the $k$ layer after coordinate transformation have the following form, respectively:

where, $∆T$ denotes temperature increment, $\left[{\stackrel{-}{Q}}_k^c\right]$ denotes the elastic constant of composite medium, ${\alpha }_x$, ${\alpha }_y$ and ${\alpha }_{xy}$ are thermal expansion coefficients of the SMA hybrid panel which can be obtained as:

Based on the one-dimensional model of SMA proposed by Brinson [7] and assuming all SMA fibers are fully constrained, the expressions for the recovery stress of SMA fibers during heating and cooling can be derived as follows, respectively [10].

During heating:

During cooling:

where, $\xi$ denotes the martensite fraction, $E\left(\xi \right)$ denotes the elastic modulus of SMA, $\theta$ denotes the thermal elastic modulus, $T$ denotes temperature and $T_0$ is the reference temperature, $\mathrm{\Omega }\left(\xi \right)$ is the phase transformation coefficient. The subscript 0 denotes initial state. $A_s^{\sigma }$ and $A_f^{\sigma }$ denote the start and finish temperatures of austenite in stress, and $M_s^{\sigma }$ and $M_f^{\sigma }$ denote the start and finish temperatures of martensite in stress. ${\xi }_s$ is the martensite fraction induced by stress. The first expression in Eqs. (13) is used for SMA in the initial martensite state, while the third expression among them is used for SMA in 100 % austenite state, and the second expression among them is used for SMA in the phase transformation state from martensite to austenite.

The transformation process from martensite to austenite (M→A) and from austenite to martensite (A→M) are given as follows, respectively:

where, $M_s$and $M_f$ denote the start and finish temperature points during the phase transformation from austenite to martensite, and $A_s$and $A_f$ denote the start and finish temperature points during the phase transformation from martensite to austenite, respectively. $C_A$ and $C_M$ are material constant of SMA fibers which determine the influence of the stress on the transformation temperature. ${\sigma }_s^{cr}$ and ${\sigma }_f^{cr}$ denote the start and finish stress points of phase transformation, respectively, and the subscript “$s_0$” denotes martensite fraction induced by stress corresponding to initial state.

In Eqs. (13) and (14), ${\sigma }_1$ and ${\sigma }_2$ denote the start and finish stress for the transformation (M→A), ${\sigma }_3$ denotes the start stress for the transformation (A→M).

The phase transformation coefficient $\mathrm{\Omega }\left(\xi \right)$ and the elastic modulus $E_s\left(\xi \right)$ can be expressed respectively as:

where, $E_M$ and $E_A$ denote Young’s modulus in the martensite and austenite phase, respectively, ${\epsilon }_L$ is recovery strain limit.

3. Solution of the governing equation

The composite panel is simply supported and the mode shapes that satisfy the displacement boundary conditions can be assumed as:

Substituting Eq. (19) into the governing Eq. (1) and applying Galerkin procedure, the following governing equations in matrix form can be found:

where $\left\{q\left(t\right)\right\}=\left[q_1\left(t\right),\dots ,q_N\left(t\right)\right]$ is generalized coordinate vector, and dot denotes the derivative with respect to time $t$. $\left[M\right]$, $\left[K\right]$ and $\left[B\right]$ are the mass and stiffness and aerodynamic influence matrices, respectively. They can be expressed as:

where $\gamma$ denotes the length to width ratio, $D_{11}^0$ denotes the bending stiffness of the composite panel when all the fibers of the composite layers are aligned in the airflow $x$ direction and $V_s$ equal to zero.

Nondimensional aerodynamic pressure is given as:

Nondimensional in-plane forces are defined as:

where $\beta$ is the length to thickness ratio.

4. Numerical results

4.1. The critical flutter dynamic pressure

Flutter behavior of the composite panels with embedded SMA fibers is studied. The composite matrix material used in the numerical examples is Graphite/Epoxy AS-3002. Its properties are listed in Table 1. The [0/90/–90/90]_s and [0/45/–45/90]_s laminates are used to examine the effect of the lay-up on flutter behavior. The material properties of SMA fibers are listed in Table 2.

Table 1The material parameters of Graphite/Epoxy AS-3002

$E_{1m}$ (GPa)	26.5 $E_{2m}$
$G_{12m}$ (GPa)	1.184 $E_{2m}$
$v_{12m}$	0.21
${\alpha }_{1m}$ (1/°C)	–0.07×10-6
${\alpha }_{2m}$ (1/°C)	30.1×10-6

Table 2Material properties of SMA wires

SMA (Nitinol)
$E_A$ / MPa	67×103
$E_M$ / MPa	26.3×103
${\sigma }_s^{cr}$ / MPa	100
${\sigma }_f^{cr}$ / MPa	170
${\epsilon }_L$	0.067
$\mathrm{\Theta }$ / (MPa/°C)	0.55
$M_f$ / °C	9
$M_s$ / °C	18.4
$A_s$ / °C	34.5
$A_f$ / °C	49
$C_M$ / (MPa/°C)	8
$C_A$ / (MPa/°C)	13.8
$\rho$ / (kg/m3)	6450

The thickness of the composite panel is 0.002 (m), $\beta =$200. The width can be obtained by $b=\beta h/\gamma$ so long as $\gamma$ is given.

Fig. 2Frequency coalescence curves of a SMA composite panel with increase of number of vibration modes N(ε0= 0.01, Vs= 0.4, T= 55°C, γ= 2)

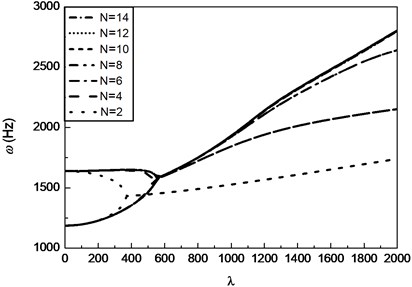
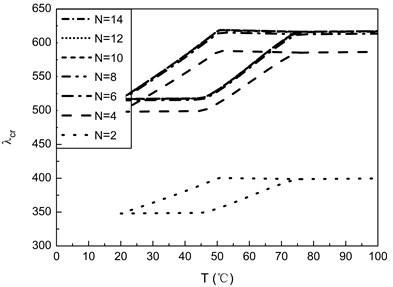
Fig. 3Flutter boundaries of a SMA composite panel with increase of number of vibration modes N(ε0= 0.01, Vs= 0.4, γ= 2)

It is necessary to examine if sufficient mode shape functions are used in the solution of the equation to obtain converged results in the case of using Galerkin method. Fig. 2 shows the frequency coalescence curves of the SMA composite panel with [0/90/–90/90]_s laminates for increase of number of vibration modes $N$. When $\lambda =$0, the eigenvalues of all modes of the panel are real. $\lambda$ may be increased from zero until the eigenvalues of two modes coalesce or become identical. This value of $\lambda$ that creates coalescence is the critical value ${\lambda }_{cr}$, where flutter occurs.

It is seen from the figure that, fourteen modes of the composite panel are enough to obtain converged solution.

Fig. 3 shows the critical flutter dynamic pressure vs. temperature curves for the SMA composite panel with [0/90/–90/90]_s laminates for increase of number of vibration modes $N$. The result shows that the approximate solution methodology developed in this paper can obtain good convergence solutions.

Based on mode convergence examination it is found that $N=$14 gives suitably converged results. So for all results given in this paper $N=$ 14 unless otherwise noted.

4.1.1. Symmetrical orthotropic panels

In this section, the symmetrical orthotropic panels with SMA fibers are considered. The stacking sequence is [0/90/–90/90]_s.

Fig. 4 presents the flutter boundaries of SMA/Graphite/Epoxy AS-3002 panels with different values of $V_s$$({\epsilon }_0=\mathrm{}$0.01, $\gamma =\mathrm{}$2$)$. As shown in Fig. 4, The critical flutter dynamic pressure of the composite panel without SMA fibers ($V_s=$0) is seen decrease linearly with increase of temperature. This is because there is not the recovery stress of the SMA fiber in this case, as a result of the stiffness softened, therefore, ${\lambda }_{cr}$ is reduced. However, it is seen from Fig. 4 that SMA fiber embedding result in significant increase of ${\lambda }_{cr}$ compared with the result of the composite panels without SMA. The phase transformation M→A is induced during heating, and the phase transformation A→M is induced during cooling. The curves of temperature-critical flutter dynamic pressure (${\lambda }_{cr}-T$) are typical hysteresis loops in a thermal cycle. ${\lambda }_{cr}$ increases with the increase in temperature during heating, but decline with the decrease in temperature during cooling. Furthermore, it can be seen that any increase of the volume fraction of SMA fibers $V_s$, leads to an obvious increase of ${\lambda }_{cr}$.

Fig. 5 presents the effect of the length to width ratio on the critical flutter dynamic pressure of the composite panels. And the increase of $\gamma$ is accompanied by the shift of these hysteresis loops towards higher critical flutter dynamic pressure. It seems that increasing $\gamma$ results in a more dynamically stable panels.

Fig. 6 presents the influence of the initial strain of the SMA fibers on the critical flutter dynamic pressure of the composite panels. As can be seen, the initial strain of SMA fiber appears to have marginal effect on ${\lambda }_{cr}$.

Fig. 4Flutter boundaries of SMA/Graphite/Epoxy AS-3002 panels with different values of Vs for [0/90/–90/90]s laminates (ε0= 0.01, γ= 2)

Fig. 5Flutter boundaries of SMA/Graphite/Epoxy AS-3002 with different values of γ for [0/90/–90/90]s laminates (ε0= 0.01, Vs= 0.4)

Fig. 6Flutter boundaries of SMA/Graphite/Epoxy AS-3002 panels with different values of ε0 for [0/90/–90/90]s laminates (Vs= 0.4, γ= 2)

Fig. 7Flutter boundaries of SMA/Graphite/Epoxy AS-3002 panels with different values of Vs for [0/45/–45/90]s laminates (ε0= 0.01, γ= 2)

4.1.2. Symmetrical anisotropic panels

In this section, the symmetrical anisotropic panels with SMA fibers are considered. The stacking sequence is [0/45/–45/90]_s. Fig. 7 presents the flutter boundaries of SMA/Graphite/Epoxy AS-3002 panels. It is plotted with different values of $V_s$. Like the symmetrical orthotropic panels, the critical flutter dynamic pressure increases as the volume fraction of SMA fibers increases.

Figs. 8 and 9 present the flutter boundaries of SMA/Graphite/Epoxy AS-3002 panels. They are plotted with different values of $\gamma$ and ${\epsilon }_0$, respectively. The results are similar to the symmetrical orthotropic case. However, it can be evidently seen by comparing results in Figs. 4-6 and Figs. 7-9 that the stacking sequence of the composite panels with embedded SMA fibers significantly affects the critical flutter dynamic pressure.

Fig. 8Flutter boundaries of SMA/Graphite/Epoxy AS-3002 panels with different values of γ for [0/45/–45/90]s laminates (ε0= 0.01, Vs= 0.4)

Fig. 9Flutter boundaries of SMA/Graphite/Epoxy AS-3002 panels with different values of ε0 for [0/45/–45/90]s laminates (Vs= 0.4, γ= 2)

4.2. Dynamical response

Fig. 10 presents the time history responses and phase plane plots of the geometric center of the panel for various dynamic pressures $(\lambda <{\lambda }_{cr}$, $\lambda >{\lambda }_{cr}$, $\lambda {=\lambda }_{cr})$.This figure is plotted for the SMA fibers in the initial martensite state during heating ($T=$30 °C). It clearly shows that when dynamic pressure is larger than the critical flutter dynamic pressure, an unstable response occurs.

Fig. 11 presents the time history response and phase plane plots of the geometric center of the panel for various dynamic pressures $(\lambda <{\lambda }_{cr}$, $\lambda >{\lambda }_{cr}$, $\lambda {=\lambda }_{cr})$. This figure is plotted for the SMA fibers in the phase transformation state from austenite to martensite during cooling ($T=$60 °C). The results are similar to the case of symmetrical orthotropic in Fig. 9. It also shows that when dynamic pressure is smaller than the critical flutter dynamic pressure, the response of the composite panel is stable.

Fig. 10Displacement response curves with time and phase plane plots during heating ([0/90/–90/90]s, T= 30 °C)

a)$\lambda <{\lambda }_{cr}$

b)$\lambda {=\lambda }_{cr}$

c)$\lambda {>\lambda }_{cr}$

5. Conclusions

An analytical model was presented for the study of the flutter behavior of the composite panels embedded with SMA fibers. The presented model was used to predict the critical flutter dynamic pressure and the aeroelastic stability. Emphasis is placed on the study of the effects of SMA activation. From the present analysis and the numerical results, the following main conclusions can be obtained.

Fig. 11Displacement response curves with time and phase plane plots during cooling ([0/45/-45/90]s, T= 60 °C)

a)$\lambda <{\lambda }_{cr}$

b)$\lambda {=\lambda }_{cr}$

c)$\lambda {>\lambda }_{cr}$

1) The effects of temperature on flutter behavior during the phase transformation are important. The curves of the critical flutter dynamic pressure vs. temperature are typical hysteresis loops in a thermal cycle. The reason underlying this phenomenon is the well-known recovery stress-temperature hysteresis behavior of SMA fibers itself.

2) The recovery stress resulted due to SMA fiber actuation significantly increases the critical flutter dynamic pressure. The effects of the recovery stress on the critical flutter dynamic pressure can be enhanced by increasing of both the initial strain and the volume fraction of SMA fibers.

3) The lay-up affects flutter behavior of the composite panels significantly, whereas the initial strain of SMA fiber appears to have marginal effect on flutter behavior of the composite panels.