A hybrid artificial neural network with Dempster-Shafer theory for automated bearing fault diagnosis

2.1. Data collection

The data used in this study was downloaded from the website of Case Western Reserve University Bearing Data Center specifically to represent ball bearing healthy and faulty conditions (rolling element, inner raceway, and outer raceway faults). The arrangement of the test rig used to simulate different conditions of the bearing is shown in Fig. 1. The test rig consists of a 2 hp motor, a torque transducer, and a dynamometer. A 7 mils (178 microns) fault diameter was introduced to the SKF bearing to simulate bearing faults. The motor was operating at approximately 1772 rpm with 1 hp load. Vibration data was collected at a sampling rate of 12,000 samples per second by accelerometers that were attached to the bearing housing.

Fig. 1Test rig for the experiment

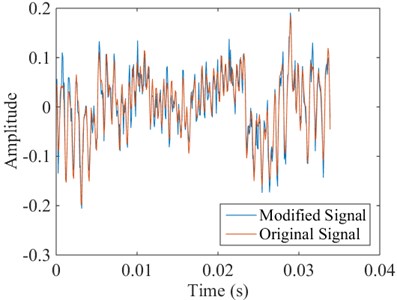
To simulate industrial environment where bearing vibration signals would be contaminated with random noise, white Gaussian noise was added to the original vibration signal. Fig. 2 shows the original vibration signal and the modified signal with additive white Gaussian noise. As a result, the signal-to-noise ratio (SNR) of the modified signal is 10 dB. A total of 1,000 sets of vibration time series were extracted from the time domain vibration signal. Then, the 1,000 sets of vibration data were divided into two different inputs of which one set of the data was used to train the machine learning model, and the other set of the data was used for model validation. The distribution of the vibration data set employed in this study is shown in Table 1. The next section describes the statistical analysis methods and parameters such as root-mean-square (RMS), standard deviation ($\sigma$), skewness, kurtosis, and crest factor that are used in features extraction for machine learning diagnostic study.

Fig. 2Comparison of original vibration signal and the modified signal with additive white Gaussian noise

2.2. Statistical analysis

The 1,000 sets of vibration data were used as the input for statistical analysis and subsequently the resulted statistical parameters were used as features for ANN model training and testing purposes. Each statistical analysis method is briefly described in the following paragraphs.

The RMS value of a vibration time series can be used to represent the power content of a vibration signal. This feature is known to be effective in detecting an imbalance in rotating machinery [2]. Eq. (1) shows the mathematical function of RMS:

Standard deviation ($\sigma$) of a vibration time series denotes the energy content of the vibration signal. It is also a measure of discrimination [3]. Eq. (2) shows the mathematical function of standard deviation:

Skewness measures the degree of asymmetry of a distribution around its mean. It is a dimensionless parameter which is also an effective parameter to be used for fault diagnosis in rotating machinery [4]. Eq. (3) shows the mathematical function of skewness:

Kurtosis is a statistical parameter that describes the distribution of the data around the mean. It characterizes the degree to which a statistical frequency curve is peaked [5]. Also, it is also a dimensionless parameter. Eq. (4) shows the mathematical function of kurtosis:

Crest factor is a ratio of the peak value to its RMS value of an input signal. It can be used to identify changes in the signal pattern due to impulsive vibration sources such as for ball bearing defects on the outer raceway [2]. Eq. (5) shows the mathematical function of crest factor:

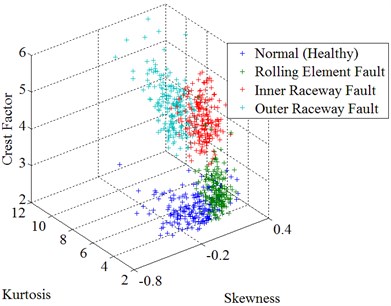
Fig. 3 shows the data distribution of skewness, kurtosis, and crest factor for all experimental bearing conditions respectively.

Since there is a total of 250 samples for each bearing condition, 80 % of the samples were selected randomly as the training data to synthesize the machine learning model while the remaining 20 % of the samples were used to validate the trained machine learning model. The distribution of all training data of the three feature parameters (skewness, kurtosis, and crest factor) used in this study is shown in Fig. 4.

Fig. 3Data distribution of skewness, kurtosis, and crest factor for all experimental bearing conditions

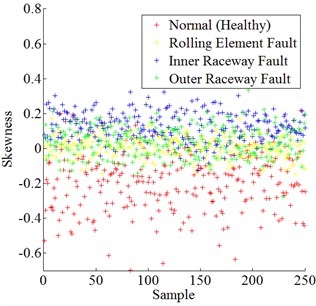
a) Skewness of all bearing conditions

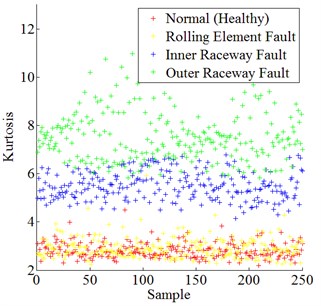
b) Kurtosis of all bearing conditions

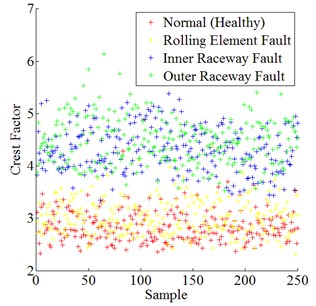
c) Crest factor of all bearing conditions

Fig. 4Distribution of all training data

3.1. Artificial neural network

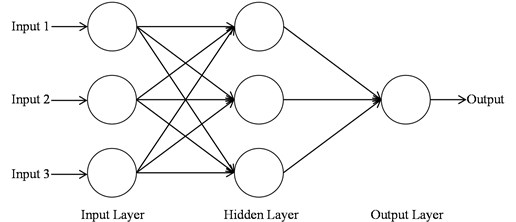
Over the past century, there has been a dramatic increase in the application of ANN in various fields, including machinery faults diagnosis. ANN is a supervised machine learning theory. ANN form a parallel information processing arrangement based on a grid of interconnected artificial neurons as shown in Fig. 5 [6].

There are two phases in ANNs: the training phase and the testing phase [7]. The training phase aims to determine the type of tasks that can be solved later while the testing phase seeks to process the representative features of the inputs. Lee et al. [8] reviewed characteristics of commonly used algorithms such as ANN, SVM, Bayesian Belief Networks (BBN), Hidden Markov Model, and Feature Map. for machinery faults diagnostics. Finally, they nominated ANN as the most appropriate tool for machinery faults diagnostics.

Fig. 5Schematic structure of an Artificial Neural Networks

3.2. Dempster-shafer theory

The DS theory was the seminal work of Glenn Shafer (1976) and its conceptual forerunner by Arthur P. Dempster (1967). It is a mathematical theory that deals with uncertain information reasoning. It allows the combination of evidence from multiple sources and provides a measure of confidence (belief function, $Bel$) that a given event will occur. Let $\mathrm{\Theta }$ be a finite set of possible answers, and $\varphi$ represents an empty set; the belief function should satisfy the three axioms represented by Eqs. (6-8):

The DS theory consists of three important parameters, namely the mass function ($m$), belief function ($Bel$) and plausibility ($Pl$). Mass function ($m$) is a basic probability assignment that measures the belief that is committed exactly to a subset. Belief function ($Bel$) is a lower probability that measures the total belief mass that is confined to a subset while plausibility ($Pl$) is a higher probability that measures the total belief mass that can move into a subset.

The most recent applications of DS theory can be found in the fields of medical diagnostic [9], aviation [10], machinery condition monitoring and fault diagnosis [11, 12], maintenance management [13], chemical engineering [14], defence [15], power generation industry [16] and engineering design [17], to name a few. To date, DS theory has been proven to be effective in combining evidence to provide a high level of confidence in the occurrence of an event.

3.3. Structure of bearing fault diagnosis model

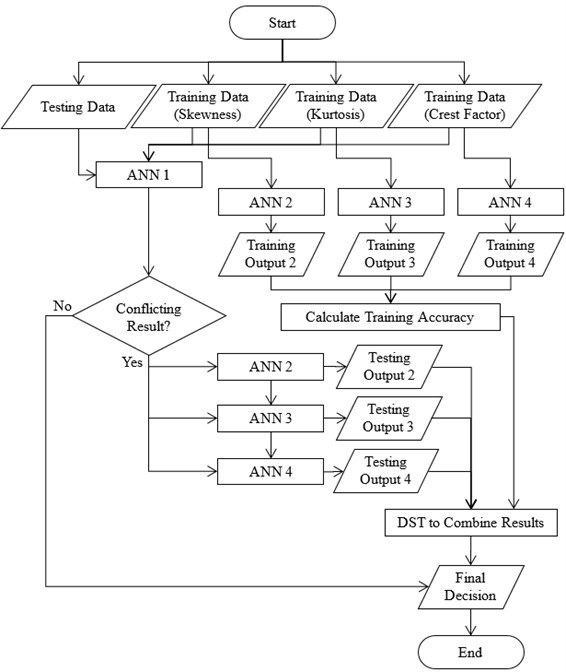
The automated bearing fault diagnosis model in this study was constructed by combining the ANN and DS theory. This is a two layers classification. First layer: an ANN model will be constructed by feeding training data from all features (skewness, kurtosis, and crest factor) to the ANN algorithm. Then, testing data will be used to test the trained ANN algorithm. In this stage, some of the testing data may have the conflicting result as illustrated in Table 2. Second layer: three ANN models will be constructed by feeding training data from each feature respectively, meaning that an ANN model will be built on training data from a single feature only (e.g. skewness). The testing data with conflicting result produced in the first layer will be classified by the second layer classification. This second layer classification model combines all the three ANN models (skewness, kurtosis, and crest factor) by DS theory. The ANN models with single feature generated a better classification curve fitting that capable of distinguishing the samples fell on the border of the first layer classification and provide the final decision on a bearing’s condition. A flowchart for the automated bearing fault diagnosis model used in this study is shown in Fig. 6.

Fig. 6Flowchart for the automated bearing fault diagnosis

4.1. ANN results and discussion

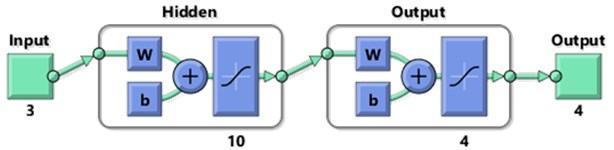
In the first layer of bearing conditions classification, ANN has classified most of the testing data into four bearing conditions which are healthy, rolling element fault, inner raceway fault, and outer raceway fault. The ANN structure used in this study is a feed-forward back propagation neural network with two layers and ten neurons on the first layer. Besides, Levenberg-Marquardt training algorithm (trainlm) has been employed in this study. It is generally considered as the fastest training function. The ANN structure was shown in Fig. 7. The ANN’s training performance progress was shown in Fig. 8. The training performance plot showed the validation curve is analogous to test curve. In other words, it does not indicate any major problem in the training stage such as overfitting problem. The validation performance reached a minimum at 12 iterations. Fig. 9 shows the regression plot of the ANN. The plot demonstrates the relationship between the outputs of the ANN and the targets during its training, validation, and testing stage. The ideal situation is all ANN’s outputs exactly same as targets which mean all data were classified correctly. However, this situation rarely happens in the real practice. When the value of $R$ closer to 1, it indicates better the relationship between outputs and targets. In this study, the regression plot showed the value of $R$ is about 0.9 for all training, validation, testing stages which indicate a good relationship between outputs and targets. Therefore, the authors able to summarize the performance of the ANN model are acceptable.

Fig. 7The ANN structure in this study

The results generated by the ANN model were analyzed. However, some conflicting results were generated as shown in Fig. 10. The conflicting results were then classified by the second layer classification which employed DS theory for results fusion.

Fig. 8The ANN’s training performance. Best validation performance is 0.036211 at epoch 12

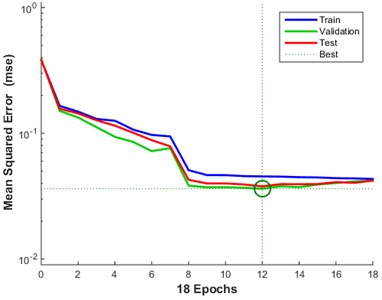
Fig. 9The ANN’s regression

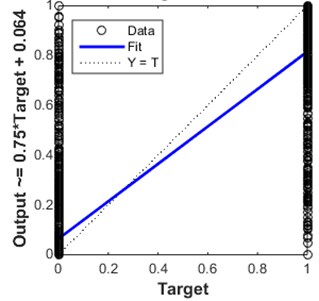
a) Training $R=$ 0.87064

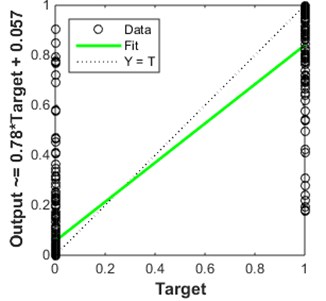
b) Validation $R=$0.89868

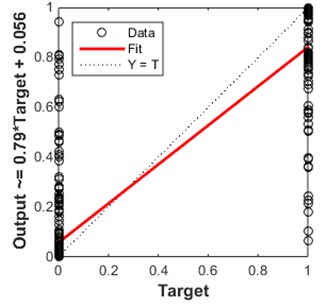
c) Test $R=$0.8935

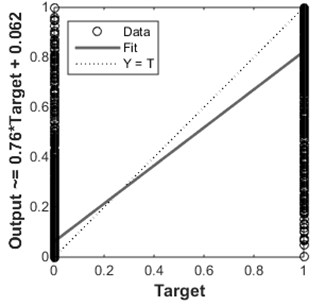
d) All $R=$0.87832

Fig. 10Analysis of decisions of ANN models

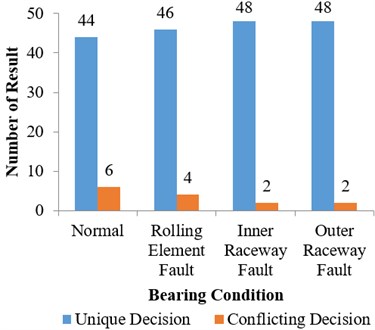
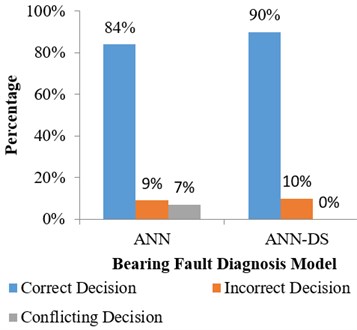
Fig. 11The accuracy of decisions by ANN and ANN-DS

4.2. DS theory results and discussion

In this phase, the conflicting results of ANN model can be further analyzed or fused by DS theory to eliminate the conflicting decisions to arrive at the final result of bearing fault diagnosis. The inputs data of the conflicting results were sent to each ANN models which are skewness, kurtosis, and crest factor for classification. Finally, the results generated by each ANN models will be combined with DS theory to make the final decision. Fig. 11 shows the comparison of decisions making from the ANN model and the hybrid ANN-DS model. In summary, these results indicate that the hybrid ANN-DS can eliminate all conflicting decisions of ANN model and to make the final decision on the data in hand.

The accuracy of the ANN and the hybrid ANN-DS model is 84 % and 90 % respectively. Even though the increasing of accuracy is small but it was proven to be effective in eliminating conflicting results by using the hybrid ANN-DS model for bearing fault diagnosis. The increase in accuracy of the hybrid model was attributed to the elimination of conflicting decisions of the ANN model. In particular, the hybrid model was able to increase the accuracy of ANN model by 6 %.