Research on optimized layout of bridge sensors based on MAC stepwise addition and subtraction algorithm

3.1. Effective independence method (EIM)

The basic idea of the traditional EIM [13-15] is to start from the vibration modes of the target structure, such as acceleration, strain and displacement, and make use of the characteristics of the composite mode $E$ matrix to remove the measuring points from the original measuring point group of the structure. Based on the minimum error criterion, the Fisher information matrix is optimized and improved by sequentially deleting the degrees of freedom of the measuring points that contribute the least to the Fisher information matrix. Via the idempotent form of the composite mode $E$ matrix, the most appropriate number of sensors is selected to obtain the linear independent mode shape of the target structure as much as possible, so as to distinguish preferably the real state of the target structure.

$E$ matrix is an idempotent matrix, which means that $E=E^2$, its eigenvalue is 1 or 0, and the $i$th element on its diagonal represents the contribution of the $i$th degree of freedom or the test point to the matrix or rank (trace), that is, the contribution to the matrix $A_0$ [16]. Therefore, $E$ represents the effective independence distribution of the set of candidate sensor locations. The element on the diagonal of $E$ represents the linearly independent contribution of the corresponding sensor candidates to the modal matrix, namely:

When $E_{rr}=$0, it means that the corresponding mode cannot be identified at the corresponding measuring point $r$. When $E_{rr}=$1, it means that the corresponding measuring point on the $r$th measuring point is a key measuring point and cannot be excluded. The priority order of each candidate point is sorted according to the value of $E_{rr}$.

The iterative algorithm is used to eliminate the measuring points with the smallest $E_{rr}$ each time, and then the next iteration is performed until the corresponding number of sensor layout is reached. The effective independence method can maintain the linear independence of the modal matrix and the integrity of the Fisher information matrix as much as possible through this iterative algorithm, and can basically retain the modal characteristics of the original structure, so that the optimal modal characteristics can be obtained from the limited modal data.

3.2. Kinetic energy method (KEM)

The Kinetic Energy Method [17-18] is based on the connection between the modal strain energy and the response in the degrees of freedom. The modal strain energy curve is drawn by the strain modal values of each degree of freedom in the vibration response. According to the strain values of each degree of freedom, sensors are arranged in the place where the strain is large so as to achieve the purpose of structural state identification.

The Kinetic Energy Matrix (KEM), proposed by G. Heo in 1997 [19], uses the quality matrix to weigh the Fisher information matrix $Q$, and is defined as follows:

Via orthogonally decomposing of the mass matrix $M$, the following equation can be obtained:

Substituting Eq. (4) into Eq. (3), the following equation can be obtained:

If to suppose $\mathrm{\Psi }=V\mathrm{\Phi }$, then:

The modal kinetic energy of each test degree of freedom can be obtained through Eq. (6), $K{E}_D$:

Therefore, after calculating $\mathrm{\Psi }$, the modal kinetic energy of each degree of freedom can be obtained. Then the sensor position can be optimized according to the iterative optimization method for deleting the smallest diagonal element.

Based on the modal kinetic energy characteristics, the sensor configuration using this method has fair noise immunity. However, the accuracy of this method is closely related to the meshing precision of the finite element model, and the element meshing thickness may affect the distance of the sensor distribution, which has a great influence on the measured parameters that truly reflect the structural state [20].

3.3. MAC method based on QR decomposition

The choice of the initial position of the measuring point will greatly affect the working time consumption and accuracy of the later position optimization. Therefore, when using the MAC method to optimize the layout of sensors, the selection of initial measurement points is very important. The more reasonable the selection of preliminary measuring points will be, the simpler the optimization of later measuring points will be.

Therefore, the concept of QR decomposition was introduced in order to optimize the selection of initial measuring points. Using the effective independence method, the maximum norm was determined for Fisher information matrix $A_0$ as:

Therefore, after selecting an appropriate ${\mathrm{\Phi }}_n$, a Fisher information matrix that satisfies the conditions can be obtained. And QR decomposition method can be obtained by norm processing.

Let us suppose that the subset of measurable degrees of freedom of a finite element model is $\mathrm{\Phi }$, $\mathrm{\Phi }\in R_{n\times r}$, then the number of measuring points $r<n,$ and $r\left(\mathrm{\Phi }\right)=r$, that is, the matrix $\mathrm{\Phi }$ is a full rank matrix. Since the column pivot element selects a subset of the column vector group for QR decomposition, and the row space characteristic of the measurement vector is utilized. Therefore, QR decomposition of its column pivot can be obtained as follows:

where $Q\in R_{r\times r}$, $R\in R_{n\times r}$, $E\in R_{n\times n}$, $E$ are Permutation Matrices. The extraction of subset with larger norm in Φ row vector set provided initial measuring points for the MAC method [21].

After selecting the initial measuring points, their layout could be optimized. In this stage, the sequential method is mainly used for processing, and the traditional sequential method can be subdivided into two methods, that is, stepwise addition method and stepwise subtraction method.

4.1. Simulation model

In order to verify the above measuring point optimization method, this paper selected a cantilever simply supported beam model [24] for the optimization analysis of the measuring point layout. The first five-order natural frequency and vertical displacement mode shape of the structure were extracted as the basic parameters for the optimization of the measuring point position. The dimensions and element division of the simply supported beam are shown in Fig. 1, and the first five natural frequencies are listed in Table 1.

Fig. 1Cantilever simply supported beam model and element division (unit: cm)

4.2. Contribution value solution of effective independence method and kinematic energy method

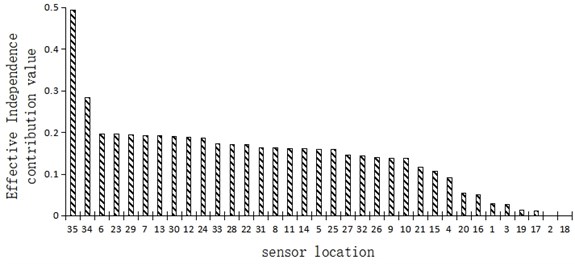
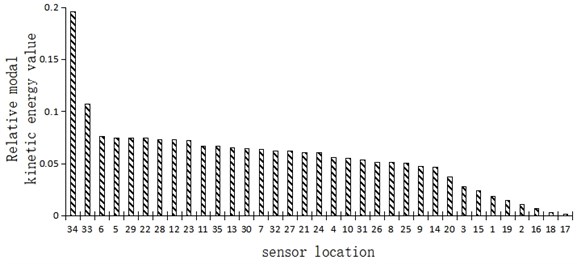
EIM and KEM methods can be used to obtain effective independent contribution values and relative modal kinetic energy values for different measurement points as shown in Figs. 2(a) and 2(b).

Fig. 2Contribution values for each measuring point

a) Effective independence contribution value

b) Relative modal kinetic energy value

Fig. 2(a) shows the effective independent contribution values for different measuring points of a simply supported cantilever beam. It can be seen that the effective independence of elements 35 and 34 and other cantilever end positions was the strongest, followed by that of elements 6, 7, 23 and 29 and other one-third section positions, and the effective independence of elements 2 and 18 and other fulcrum positions was the weakest.

Fig. 2(b) shows the relative modal kinetic energy values of the simply supported cantilever beams at different measuring points. It can be seen that the relative modal kinetic energy of elements 34 and 33 and other cantilever end positions was the strongest, followed by that of elements 5, 6, 29 and 22 and other one-third section positions, and the relative modal kinetic energy of elements 17 and 18 and other fulcrum positions was the weakest.

It can be seen from the above analysis that the effective independent contribution value and the relative modal kinetic energy value of the cantilever simply supported beam structure generally had a similar distribution trend – the strongest near the cantilever end, followed by the position at the third section, and the weakest near the fulcrum position.

4.3. Comparative analysis of results

4.3.1. MAC matrix comparative analysis

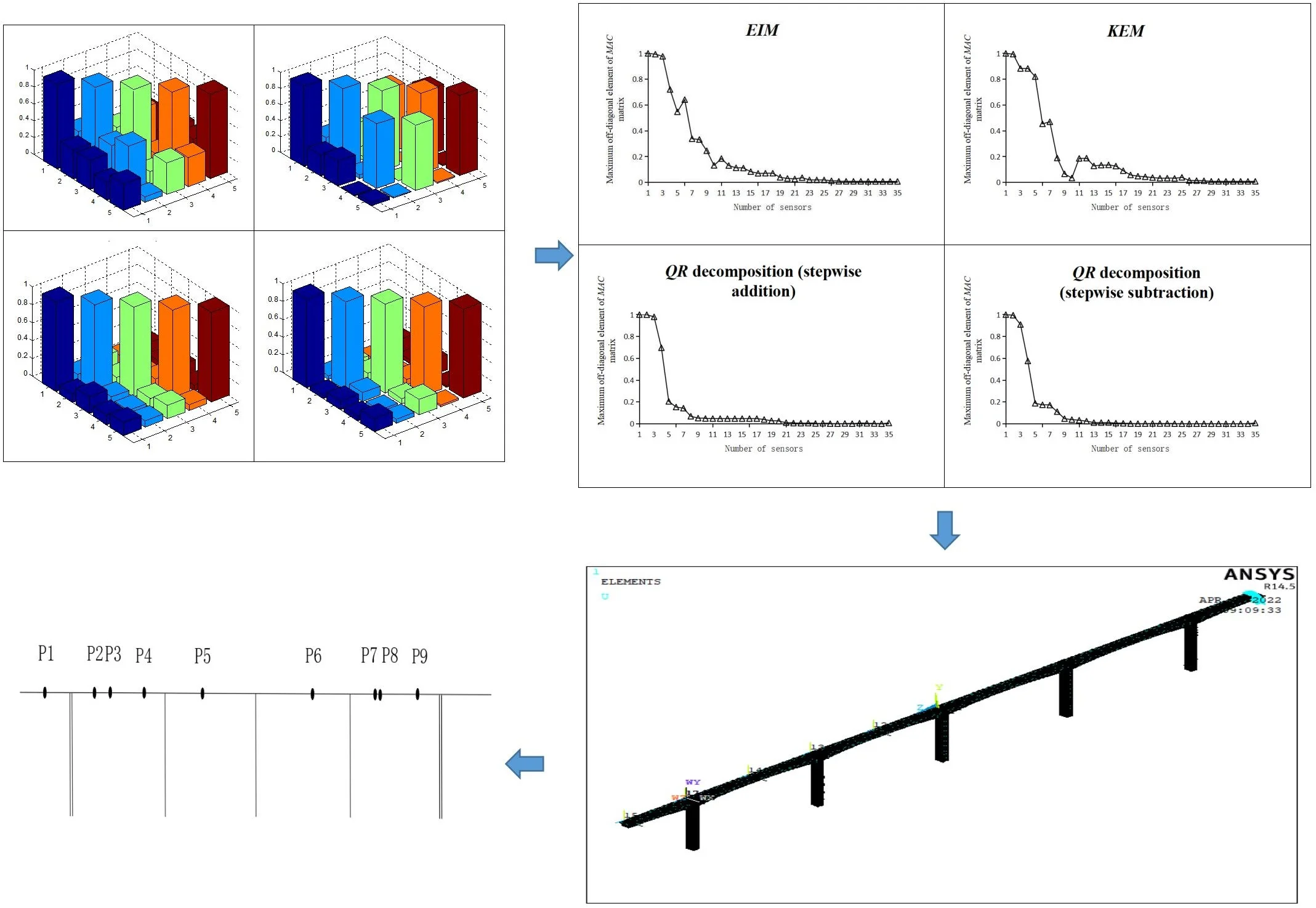
The smaller the off-diagonal element of MAC matrix is, the more independent the position of measuring points is, and the more accurately the real state of the structure can be reflected. In order to compare this matrix with the principle consisting in laying sensors on all elements of a cantilever simply supported beam, the EIM, KEM, stepwise addition method and stepwise subtraction method based on QR decomposition were adopted to select 5 units for laying sensors, and the layout sequence is shown in Table 2.

Table 2Sensor layout of four optimization methods

Layout methods	Sensor layout sequence
All measuring points layout	All Elements
EIM	35E, 34E, 6E, 23E, 29E
KEM	34E, 33E, 6E, 5E, 29E
Stepwise addition of QR decomposition	35E, 29E, 6E, 13E, 24E
Stepwise subtraction of QR decomposition	35E, 6E, 30E, 12E, 24E

By comparing the four layout sequences listed in Table 2, it is clear that for structures such as cantilever simply supported beams, it was the most important to test the cantilever end and then the one-third and two-thirds section. But different methods also had discrepancies in the layout sequence and position of measuring points.

The MAC matrix, three-dimensional histogram, maximum off-diagonal element and the average off-diagonal element value of the MAC matrix are shown in Table 3.

By comparing the largest off-diagonal element of the MAC matrix in Table 3, it can be seen that the value obtained by the KEM was the largest, namely 0.806; by comparing the average off-diagonal elements of the MAC matrix in Table 3, it can be seen that the value obtained by the EIM was the largest, namely 0.314. In the longitudinal comparison of the maximum and average off-diagonal metadata of MAC matrix in Table 3, when sensors were deployed at all measuring points, the off-diagonal elements of MAC matrix were small, and their maximum and average off-diagonal elements were only 0.008 and 0.004 respectively. This result also verified that the Modal Assurance Criterion could reflect the measuring point layout effect.

By comparing the EIM, KEM, stepwise addition method based on QR decomposition and stepwise subtraction method based on QR decomposition for 5 element positions, the following conclusions can be drawn: both methods based on QR decomposition could promote a satisfactory measuring points layout, especially the stepwise subtraction method; moreover, the off-diagonal element value in the MAC matrix obtained by EIM and KEM was relatively large, which reflected poor measuring points layout.

Therefore, it can be concluded that in case of using EIM and KEM to optimize the layout of measuring points, the number of selected elements should not be too small, otherwise it would be difficult to achieve a satisfactory layout effect. In addition, when EIM was used for layout, only the modal information of each degree of freedom of the structure was considered, while the influence of energy factors was ignored, resulting in poor stability of sensors layout.

Table 3Comparison of effects of different optimization methods

Optimization layout methods		MAC matrix	MAC layout	Largest off-diagonal element value	Average off-diagonal element value
All measuring points layout		$\mathrm{M}\mathrm{A}{\mathrm{C}}_{\mathrm{A}\mathrm{L}\mathrm{L}}=\left[\begin{array}{lllll}1.000& 0.003& 0.008& 0.004& 0.008\\ 0.003& 1.000& 0.003& 0.002& 0.003\\ 0.008& 0.003& 1.000& 0.003& 0.008\\ 0.004& 0.002& 0.003& 1.000& 0.003\\ 0.008& 0.003& 0.008& 0.003& 1.000\end{array}\right]$		0.008	0.004
1	EIM	$\mathrm{M}\mathrm{A}{\mathrm{C}}_{\mathrm{E}\mathrm{I}}=\left[\begin{array}{lllll}1.000& 0.350& 0.350& 0.210& 0.316\\ 0.350& 1.000& 0.431& 0.547& 0.067\\ 0.350& 0.431& 1.000& 0.149& 0.378\\ 0.210& 0.547& 0.149& 1.000& 0.347\\ 0.316& 0.067& 0.378& 0.347& 1.000\end{array}\right]$		0.547	0.314
2	KEM	$\mathrm{M}\mathrm{A}{\mathrm{C}}_{\mathrm{K}\mathrm{E}\mathrm{M}}=\left[\begin{array}{lllll}1.000& 0.263& 0.314& 0.010& 0.037\\ 0.263& 1.000& 0.044& 0.806& 0.011\\ 0.314& 0.044& 1.000& 0.003& 0.820\\ 0.010& 0.806& 0.003& 1.000& 0.013\\ 0.037& 0.011& 0.820& 0.013& 1.000\end{array}\right]$		0.806	0.232
3	QR decomposition (stepwise addition)	$\mathrm{M}\mathrm{A}{\mathrm{C}}_{\mathrm{Q}\mathrm{R}+}=\left[\begin{array}{lllll}1.000& 0.087& 0.140& 0.103& 0.187\\ 0.087& 1.000& 0.149& 0.067& 0.008\\ 0.140& 0.149& 1.000& 0.115& 0.205\\ 0.103& 0.067& 0.115& 1.000& 0.042\\ 0.187& 0.008& 0.205& 0.042& 1.000\end{array}\right]$		0.205	0.118
4	QR decomposition (stepwise subtraction)	$\mathrm{M}\mathrm{A}{\mathrm{C}}_{\mathrm{Q}\mathrm{R}-}=\left[\begin{array}{lllll}1.000& 0.098& 0.188& 0.105& 0.148\\ 0.098& 1.000& 0.091& 0.067& 0.073\\ 0.188& 0.091& 1.000& 0.105& 0.149\\ 0.105& 0.067& 0.105& 1.000& 0.061\\ 0.148& 0.073& 0.149& 0.061& 1.000\end{array}\right]$		0.188	0.108

4.4. Layout comparative analysis

Table 4 shows the layout of the five measuring points screened by EIM, KEM, and stepwise addition method based on QR decomposition and the stepwise subtraction method based on QR decomposition.

Table 4 intuitively shows the layout of measuring points screened by different methods. It can be seen from that in terms of uniformity of measuring points layout, QR- > QR₊> EIM > KEM. Such result further verified the accuracy of the results specified in Table 3. Therefore, by observing the uniformity of measuring points layout, the superiority of the layout schemes could be assessed to a certain extent.

4.5. Optimal number of sensors

The above series of analyses were carried out based on the application of 5 measuring, but variation in the number of measuring points would also affect the optimization effect. In this section, the optimal number of sensors was selected by increasing the number of sensors one by one.

Table 4Measuring point layout of four optimization methods

Node number	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35
Element division
EIM						■																	■						■					■	■
KEM					■	■																							■					■	■
Stepwise addition of QR decomposition						■							■											■					■						■
Stepwise subtraction of QR decomposition						■						■												■						■					■
Note	■ means that the sensors arranged on the node

Figs. 3(a-d) show the comparison of the maximum off-diagonal element values of the MAC matrix and the change trend in the number of sensors obtained by using EIM, KEM, stepwise addition method based on QR decomposition and stepwise subtraction method based on QR decomposition.

Fig. 3Curve of maximum off-diagonal element of MAC and number of sensors

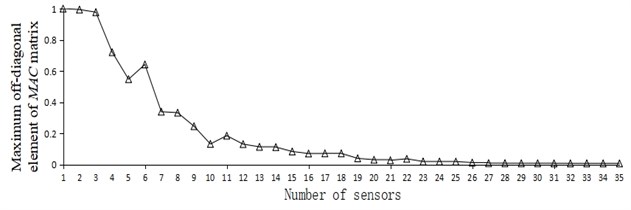
a) EIM

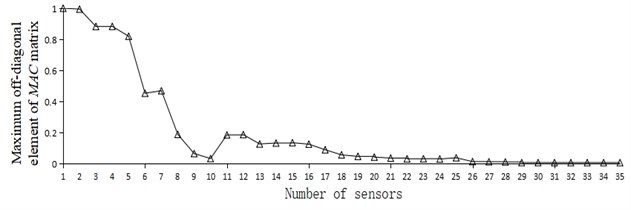
b) KEM

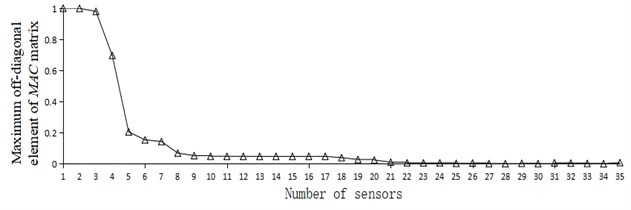
c) Stepwise addition of QR decomposition

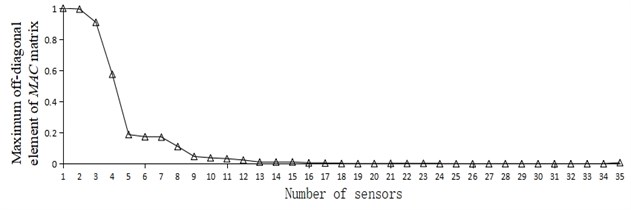
d) Stepwise subtraction of QR

It can be seen from Fig. 3 that no matter which layout scheme was adopted, with the increase of the number of sensors deployed on the measuring point, the maximum off-diagonal element of the MAC matrix showed a decreasing trend. By observing Fig. 3(a-d), it is apparent that the corresponding ordinate data in Fig. 3(c) and 3(d) declined significantly earlier than in Fig. 3(a) and 3(b), indicating that the method based on QR decomposition had better optimization foundation.

According to the research of relevant scholars [25], when the Modal Assurance Criterion was adopted for the optimal layout of measuring points, the maximum off-diagonal element value of MAC matrix was generally not greater than 0.25. Table 5 lists the number of sensors when the maximum off-diagonal element value was less than 0.25 and reached a very small steady state by different methods.

After comprehensive consideration of economic cost and test accuracy, the scheme adopted for the cantilever simply supported beam structure was determined as per the stepwise subtraction method based on QR decomposition. The number of sensors was set as 9, and the maximum off-diagonal element was 0.047.

5.1. Background of proposed new method

It can be seen from the above theoretical analysis and numerical case that the MAC matrix composed of the modal information for the measuring points can reflect the state information of the whole structure. Therefore, this study is focused on how to screen out the appropriate number and layout of the sensors. Although the layout methods of EIM, KEM, QR₊ and QR- could screen out a suitable number of measuring points for sensor layout, these methods were weak more or less in terms of over-reliance on the selection of initial measuring points, excessive number of measuring points and poor layout uniformity, and may not necessarily reflect the modal information of the complete structure, resulting in poor screening effect of measuring points. In view of this, an optimization method based on QR decomposition was proposed in this section.

5.2. Number of sensors

The measuring point optimization layout method proposed in this section was mainly divided into two stages: the first stage was based on the conventional EIM, KEM and QR decomposition methods to select the initial measurement points. The second stage consisted in the replacement and adjustment based on the initial measuring point group. A larger normal measuring point obtained by QR decomposition was selected from the remaining measurement points and added to the selected measuring point group, and then a smaller normal measuring point obtained by QR decomposition was subtracted, and the number of measuring points remained unchanged. The cyclical iteration process, which took place until the optimal measuring point layout was obtained, is shown in Fig. 4.

Fig. 4Processing procedure as per optimal sensor layout method based on stepwise addition and subtraction of number of measuring points

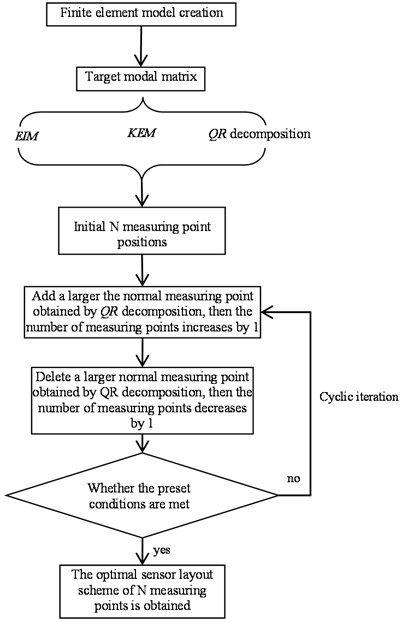
5.3. Verification of numerical case as per new method

In order to verify the effectiveness of the proposed method and facilitate the comparison with conventional methods, 5 sensor measuring points were preset in this section. MATLAB software was used to compile the corresponding calculation program, and the results after stepwise addition and subtraction could be obtained as shown in Table 6.

Table 6 lists the screening results of the initial measuring points and the processing results after the stepwise addition and subtraction of measuring points one by one as per the EIM, KEM and QR decomposition method. Clearly, the optimization effect was greatly improved after the sensor addition and subtraction process.

If to compare the changes of the maximum off-diagonal element, the KEM stepwise addition and subtraction method had the best optimization effect, because the maximum off-diagonal element decreased from 0.806 to 0.081, and the efficiency increased to 90 %.

If to compare the changes of the average off-diagonal element, the consolidated stepwise addition and subtraction method based on QR decomposition had the best optimization effect, because the average off-diagonal element decreased from 0.118 to 0.006, and the efficiency increased to 95 %.

According to the relevant data listed in Table 6, a comprehensive comparative analysis of the above three methods of optimal measuring point layout revealed that the optimal measuring point layout obtained by the consolidated stepwise addition and subtraction method based on QR decomposition was the best since various adverse effects of the initial measuring point layout could be basically eliminated, and the optimal layout with five sensors could be obtained.

6.1. Project overview

A large-span prestressed concrete continuous rigid-frame bridge has a total length of 1170 meters and a span of 2×(62.5+4×115+62.5) meters. The ANSYS finite element software was used to model the bridge and analyze its load. The whole bridge was divided into 143420 elements and 224098 nodes. The main beam was made of C55 concrete, the elastic modulus $E=$3.55×10⁴Pa, the pier column was made of C40 concrete, and the elastic modulus $E=$3.25×10⁴Pa, Poisson’s ratio was 0.2, density was $\rho =$2.55×10³kg/m³. The lateral and longitudinal constraints were simulated by COMBIN14 spring elements, and the beam end supports were consolidated by vertical constraints. The finite element model is shown in Fig. 5.

6.2. Optimal layout scheme

Fig. 6 shows the optimal layout scheme of the main beam obtained by using the EIM, KEM, stepwise addition method based on QR decomposition, stepwise subtraction method based on QR decomposition and consolidated stepwise addition and subtraction method based on QR decomposition with 9 sensors for this continuous rigid-frame bridge project.

Fig. 5Finite element model of concrete continuous rigid frame bridge

Fig. 6Comparison of layouts of different measuring point optimization schemes

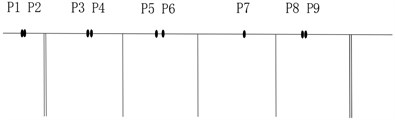
a) EIM

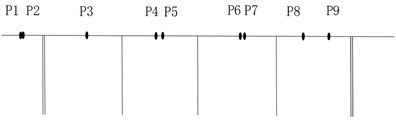
b) KEM

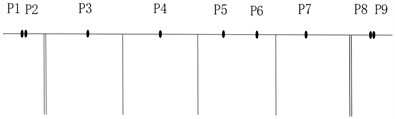
c) QR decomposition-stepwise addition

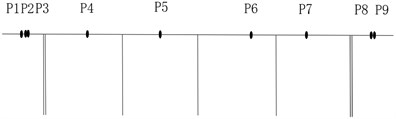
d) QR decomposition-stepwise subtraction

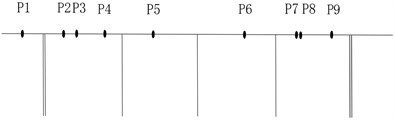
e) Consolidated QR decomposition-stepwise addition and subtraction

It can be seen from Fig. 6 that when the EIM or KEM was used, the layout of measuring points was more concentrated, because more measuring points were arranged in a concentrated area where the effective kinetic energy value was large. The basic idea of the method based on QR decomposition was to make the primary selection of measuring points based on a larger norm subset, so the position of the obtained measuring points will be more reasonable. Combined with the characteristics of the bridge type, the layout scheme of Fig. 6(d) using consolidated stepwise addition and subtraction method proposed in this study was adopted. Via this method, the measuring point positions were relatively uniform, and the layout density of the bridge spans such as side spans and middle spans were also considered. Therefore, the new method proposed was the most reasonable and can be used as a reference for the on-site sensor layout scheme.

Considering the actual engineering requirements, the number of measuring points was further expanded to 19. The layout scheme of measuring points for the main beam of continuous rigid frame bridge processed by the EIM, the KEM, stepwise addition method based on QR decomposition, stepwise subtraction method based on QR decomposition and consolidated stepwise addition and subtraction method based on QR decomposition is shown in Table 7.

Table 7 demonstrates that after the measuring points were optimized by the consolidated stepwise addition and subtraction method, the positions of the selected measuring points were more uniform, which could meet the actual monitoring requirements of the project.