An improved homotopy analysis method with accelerated convergence for nonlinear problems

1. Introduction

There are various types of nonlinear problems in the engineering field, most of which are strongly nonlinear and do not have an analytical solution. To date, many powerful methods have been developed to solve nonlinear differential equations, such as the Krylov-Bogoliubov-Mitropolsky (KBM) [1-3], the method of harmonic balance [4-6], Adomian’s decomposition method (ADM) [7, 8] and the small parameter method [9-11]. However, these methods cannot provide us with a simple way to adjust and control the convergence region and rate of approximate solution series. The homotopy analysis method (HAM) [12-15] was proposed in 1992 by Liao [16]. Based on the homotopy of topology, the advantage of the HAM is that it is independent of a small or large physical parameter and provides a way to control and ensure the convergence of approximate series. It has been proven that the HAM logically contains non-perturbations such as the Lyapunov artificial small parameter method, the ADM, the $\delta$-expansion method, the variational iteration method and so on [17, 18]. Therefore, the HAM is more general.

However, to obtain a rather accurate homotopy approximation, the high-order deformation equation must be solved, which is usually complicated to compute. And in the standard HAM, the so called $\mathrm{\hslash }$-curves must be plotted to find the optimal values of $\mathrm{\hslash }$ with which the approximations converge fastest. In this paper, we introduce an accelerated convergence method, by which the values of $\mathrm{\hslash }$ can be optimally recognized and the improved approximations converge faster than the standard homotopy approximations.

2. Basics of the HAM

One can transform a nonlinear problem into an infinite number of linear sub-problems and obtain series solutions via the homotopy analysis method, whether the nonlinear problem contains small parameters or not. Consider the following general nonlinear system:

where $L$ is a linear operator, $N$ is a nonlinear operator, $g\left(r\right)$ is a known function, $u\left(r\right)$ is an unknown function to be determined and $r$ denotes temporal or spatial independent variables. Let $u_0\left(r\right)$ denote an initial guess of the exact solution for $u\left(r\right)$, $\mathrm{\hslash }\ne 0$ denote an auxiliary convergence-control parameter, and $H\left(r\right)\ne 0$ denote an auxiliary function. Then, the homotopy function is constructed as:

where $q\in \left[\mathrm{0,1}\right]$ is an embedding parameter, $\mathcal{L}$ is an auxiliary linear operator with the property $\mathcal{L}\left(0\right)=0$, and $\mathrm{\aleph }$ is a nonlinear operator defined as:

Then, enforcing:

the zero-order deformation equation would be constructed as:

When $q=\text{0}$ and $q=\text{1}$, we have respectively:

when $q=\text{0}$, and:

when $q=\text{1}$.

It is easy to show that from Eq. (6) and Eq. (7):

Thus, as the embedding parameter $q$ increases from 0 to 1, $\mathrm{\Phi }(r;q)$ varies continuously from the initial guess $u_0\left(r\right)$ to the exact solution $u\left(r\right)$ of the original Eq. (1). Differentiating Eq. (5) $n$ times with respect to the embedding parameter $q$ and then setting $q=\text{0}$ and finally dividing them by $n!$, one can obtain the so-called $n$th-order deformation equation:

where:

for simplicity, and:

Because $\mathrm{\Phi }(r;q)$ depends on the embedding parameter $q\in \left[\mathrm{0,1}\right]$, it can be expanded into a power series of $q$ by using the Tylor theorem as:

where:

$u_m\left(r\right)$ can be found by solving Eq. (10), which is a linear equation. If the initial guess $u_0\left(r\right)$, auxiliary linear operator $\mathcal{L}$, convergence-control parameter $\mathrm{\hslash }$ and auxiliary function $H\left(r\right)$ are properly chosen, the series Eq. (14) is convergent to $\mathrm{\Phi }(r;q)$ at $q=\text{1}$, and one can have, according to Eq. (9) and Eq. (14), the homotopy-series solution:

and the $n$th-order homotopy-approximation:

3. The idea of the accelerated convergence method

Only the series solutions can be obtained for most nonlinear problems. It makes sense to ensure and accelerate the convergence of the series. Once the base functions that express the solution are chosen, the proportion of the terms of the solution is pivotal to the convergence rate. We try to introduce some ratio-control parameters in the approximate solution expressions, combined with the original governing equations and the given conditions, to control the proportion between the terms. If there are $n+1$ non-constant terms in the approximate expressions, $n$ ratio-control parameters should be introduced as multipliers of the first $n$ terms. Assume that the $x$th-order homotopy approximation of Eq. (1) can be expressed as:

Then we introduce $n$ ratio-control parameters in Eq. (18) as follows:

For initial value or boundary value problems, the values of $u\left(s\right)$, $u\text{'}\left(s\right)$, …, and $u^{\left(n\right)}\left(s\right)$ can be obtained by continuous derivation of Eq. (1) if the given conditions is at $r=s$, then an equation can be written as follows:

Note that the numbers of equations should be equal to the numbers of unknowns in Eq. (20) including the convergence-control parameter $\mathrm{\hslash }$. Sometimes Eq. (20) consists of nonlinear algebraic equations, thus there may be multiple solutions. Therefore, to choose the proper values of parameters, we can use the squared residual:

where, $v$ denotes the number of the solutions of Eq. (20) and:

Then, one can obtain the optimal values of parameters for which $E_x(a_{1,v},a_{2,v},\cdots ,a_{n,v},{\mathrm{\hslash }}_v)$ is the minimum.

Two examples are evaluated in the following to illustrate the specific method.

4. Illustrative examples

4.2. Simple pendulum attached to a rotating rigid frame[12]

The governing equation is:

34

$\ddot{\theta }+{\omega }^2(1-\epsilon \mathrm{c}\mathrm{o}\mathrm{s}\theta )\mathrm{s}\mathrm{i}\mathrm{n}\theta =0,$

subject to the initial conditions:

35

$\theta \left(0\right)=\varphi ,\dot{\theta }\left(0\right)=0.$

To apply the HAM to solve the above problem, the following approximation is used:

36

${\omega }^2\left(1-\epsilon \mathrm{c}\mathrm{o}\mathrm{s}\theta \right)\mathrm{s}\mathrm{i}\mathrm{n}\theta \approx -{\omega }^2\left(\epsilon -1\right)\theta +{\omega }^2\left(\frac{2\epsilon }{3}-\frac{1}{6}\right){\theta }^3,$

as a result, we obtain the following approximate differential equation:

37

$\ddot{\theta }-{\omega }^2(\epsilon -1)\theta +{\omega }^2\left(\frac{2\epsilon }{3}-\frac{1}{6}\right){\theta }^3=0.$

Obviously, the more terms of the Maclaurin series considered, the more efficient the solution series obtained but the more complicated the problem will be. To illustrate the validity and simplicity of the accelerated convergence method, we only use the first two terms of the Maclaurin series to approximate the original Eq. (34) as a duffing-like Eq. (37). The base functions and the initial approximation of the solution are chosen as Eq. (24) and Eq. (25), respectively. The second order approximate expressions of Eq. (37) can be easily obtained by the HAM. There are three non-constant terms in the second-order approximate expression ${\theta }_2\left(t\right)$. Thus, the improved expression ${\tilde{\theta }}_2\left(t\right)$ should contain two ratio-control parameters like Eq. (29).

The second order homotopy approximate frequency of Eq. (37) reads:

38

${\alpha }_2=\sqrt{\begin{array}{c}(1-\epsilon ){\omega }^2+\frac{3{\beta }^2{\omega }^2}{4}\left(\frac{2\epsilon }{3}-\frac{1}{6}\right)+\frac{\mathrm{\hslash }{\beta }^4{\omega }^4}{64}{\left(\frac{2\epsilon }{3}-\frac{1}{6}\right)}^2\\ +\frac{3{\mathrm{\hslash }}^2{\beta }^4{\omega }^4}{128}{\left(\frac{2\epsilon }{3}-\frac{1}{6}\right)}^2+\frac{39{\mathrm{\hslash }}^2{\beta }^6{\omega }^4}{2048}{\left(\frac{2\epsilon }{3}-\frac{1}{6}\right)}^2\end{array}}.$

Note that, to establish the simultaneous equations like Eq. (30) in this example, one should obtain the exact values of $\theta \left(0\right)$, $\ddot{\theta }\left(0\right)$, ${\theta }^{\left(4\right)}\left(0\right)$ and ${\theta }^{\left(6\right)}\left(0\right)$ by differentiating the original governing Eq. (34) continuously with respect to $t$ and using the initial conditions.

We also obtain the values of convergence-control parameter $\mathrm{\hslash }$ which minimizes the discrete squared residual in the SHAM by plotting the $\mathrm{\hslash }$-curves and compare the minimum of discrete squared residual in the SHAM and the IHAM, as shown in Table 3. To illustrate the validity of the accelerated convergence method for this example, comparison of frequency is given in Table 4.

Table 3The minimum of discrete squared residual in different cases for example 2

	$\omega =$ 1, $\epsilon =$0.5, $\varphi =\text{0.5}\pi$	$\omega =$1,$\epsilon =$0.5, $\varphi =\text{0.7}\pi$	$\omega =$1,$\epsilon =$0.9, $\varphi =\text{0.5}\pi$	$\omega =$1,$\epsilon =$0.9, $\varphi =\text{0.7}\pi$	$\omega =$2,$\epsilon =$0.9, $\varphi =\text{0.7}\pi$
$\hslash$	–0.503	–0.189	–0.219	–0.090	–0.032
SHAM	128.28	367.91	138.00	756.54	12048.3
IHAM	0.014	0.722	0.003	2.780	44.475

Table 4Comparison of α corresponding to various parameters of system for example 2

	$\omega =$ 1, $\epsilon =$0.5, $\varphi =0.5\pi$	$\omega =$1,$\epsilon =$0.5, $\varphi =0.7\pi$	$\omega =$1,$\epsilon =$0.9, $\varphi =0.5\pi$	$\omega =$1,$\epsilon =$0.9, $\varphi =0.7\pi$	$\omega =$2,$\epsilon =$0.9, $\varphi =0.7\pi$
${\alpha }_2$	0.90006070	1.05130991	0.94966034	1.29215650	2.58072027
${\tilde{\alpha }}_2$	0.79728921	0.75460788	0.74192670	0.79527954	1.59055907
exact values	0.79432027	0.74093414	0.74305823	0.76644529	1.53289057

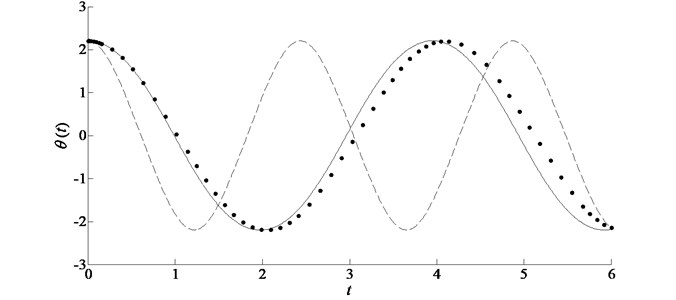
Fig. 1Comparison of the exact solution with the analytic approximations in the case of ω= 1, ε= 0.5, ϕ=0.5π for example 2. Symbols: numerical solution; solid line: improved homotopy approximation by accelerated convergence; dashed line: standard homotopy approximation by plotting ℏ-curves

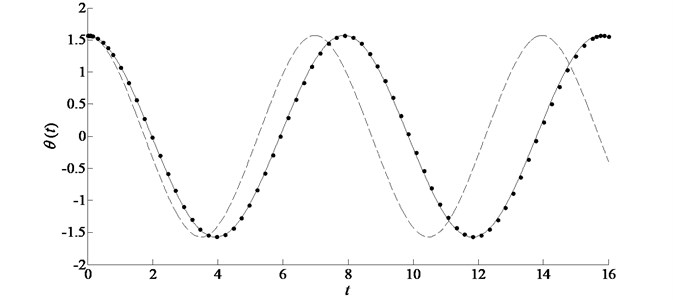
Fig. 2Comparison of the exact solution with the analytic approximations in the case of ω= 2, ε= 0.9, ϕ=0.7π for example 2. Symbols: numerical solution; solid line: improved homotopy approximation by accelerated convergence; dashed line: standard homotopy approximation by plotting ℏ-curves

5. Comparison with L-P perturbation method

Lindstedt-Poincaré perturbation method [19, 20] (L-P perturbation method) is a powerful analytical technique to weak nonlinear problems. Eq. (34) have a periodic solution. In the idea of L-P perturbation, one should express the solution $u\left(t\right)$ and the frequency squared ${\omega }^2$ in power series with respect to $\epsilon$:

where, $\left|\epsilon \right|\ll \text{1}$. By substituting Eq. (39) and Eq. (40) into Eq. (23), one obtain:

By equating coefficients of like powers of $\epsilon$, one can obtain the set of recursive linear differential equations:

and so on. By solving above equations and eliminating the secular terms, we can obtain three terms order L-P approximation as:

Fig. 3 and Fig. 4 give the solution comparisons of L-P perturbation method with SHAM and IHAM in different weak nonlinear cases.

Fig. 3Comparison of the analytic approximations in the case of ε= 0.1, A= 5 for example 1. Symbols: L-P perturbation solution; solid line: improved homotopy approximation by accelerated convergence; dashed line: standard homotopy approximation by plotting ℏ-curves

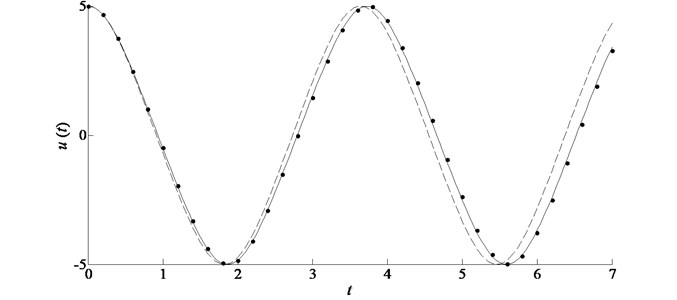
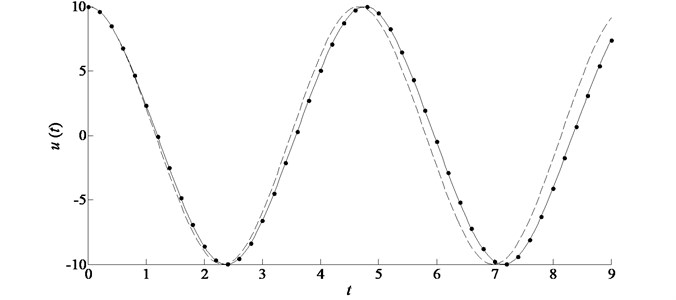
Fig. 4Comparison of the analytic approximations in the case of ε= 0.01, A= 10 for example 1. Symbols: L-P perturbation solution; solid line: improved homotopy approximation by accelerated convergence; dashed line: standard homotopy approximation by plotting ℏ-curves

6. Results and discussion

The standard homotopy analysis method (SHAM) gives us a way to control the ratio and region of approximations for nonlinear problems by choosing the values of $\mathrm{\hslash }$, thus in general it can give better solutions than other analytical methods. Without plotting $\mathrm{\hslash }$-curves, the same and even more accurate results can be obtained by improved homotopy analysis method (IHAM) in various cases, as shown in Table 1. Table 2 shows that the accelerated convergence method can give more accurate values of frequencies than $\mathrm{\hslash }$-curves. We also applied the IHAM to a problem with complicated nonlinear terms and obtained better results than ones by plotting the $\mathrm{\hslash }$-curves in different cases, as shown in Table 4, Table 5, Fig. 1 and Fig. 2. This successful application means that the problems with complicated nonlinear terms can be reduced to simple ones. One can only analyze simplified duffing-like equations by the HAM and obtain greatly accurate results of the original problems by the accelerated convergence method. For weak nonlinear problems, L-P perturbation can give accurate enough approximate solution. Comparison with L-P perturbation reveals that IHAM is of high accuracy for various cases, as shown in Fig. 3 and Fig. 4.

7. Conclusions

In this paper, we proposed an accelerated convergence method and improved the HAM. Faster convergent results can be obtained by our method than plotting the $\mathrm{\hslash }$-curves. The idea of the method is to control the proportion between the homotopy approximation terms by introducing some ratio-control parameters in the approximate solution expressions. All artificial parameters including the so called convergence-control parameter $\mathrm{\hslash }$ can be optimally identified by solving algebraic equations. The current work has elucidated the validity and justifications of this combination.