Vibro-acoustic coupled analysis excited by correlated turbulent boundary layer

Li, Yanbin; Fei, Qingguo; Wu, Shaoqing; Zhang, Peng; Jiang, Dong

doi:10.21595/jve.2016.16831

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 August 2016

Check for updates

Vibro-acoustic coupled analysis excited by correlated turbulent boundary layer

Yanbin Li¹

Qingguo Fei²

Shaoqing Wu³

Peng Zhang⁴

Dong Jiang⁵

^{1, 2, 3, 4}Department of Engineering Mechanics, Southeast University, Nanjing 210096, China

^{1, 2, 3, 4}Jiangsu Key Laboratory of Engineering Mechanics, Southeast University, Nanjing 210096, China

⁵College of Mechanical and Electronic Engineering, Nanjing Forestry University, Nanjing 210037, China

Corresponding Author:

Qingguo Fei

Cite the article Download PDF

Downloads 1841

WoS Core Citations 3

CrossRef Citations 3

Abstract

Vibro-acoustic coupling is one of the most concerned problems in the design stage of aircraft and aerospace vehicle. An algorithm that integrates the finite element method (FEM), the boundary element method (BEM) and an acquisition method of excitation correlation is proposed to conduct the vibro-acoustic coupled analysis under correlated excitations in time and spatial domains. The Corcos/Smol’yakov-Tkachenko (ST) power spectral density models are adopted for the correlated excitation with a divisional method, and the vibro-acoustic coupled analysis of complex structures can be greatly simplified. First, a simply supported panel under correlated TBL is investigated to validate the proposed algorithm. Then, the proposed algorithm is applied to a stiffened panel to carry out the vibro-acoustic coupled analysis under three types of excitation: (a) perfectly correlated TBL, (b) partially correlated TBL based on the Corcos or ST model, and (c) uncorrelated TBL. Parameters which may affect the vibro-acoustic coupled analysis, such as the coupled effect, the correlation of excitation and the speed and thickness of the turbulence, are also discussed. Results show that the proposed method is suitable for the vibro-acoustic coupled analysis of complex systems under correlated random excitations. The vibro-acoustic coupling effect will result in a decrease in both the natural frequency and structural response under perfectly correlated excitation, and an increase in the structural response for partial correlated and uncorrelated excitations. However, the coupling effect has little influence on the acoustical response. The structural and acoustic responses due to partially correlated excitation are larger than that due to perfectly correlated excitation. Moreover, the structural and acoustic responses increase with the increment in turbulence speed and thickness, and the difference among the responses under the three different types of excitations rapidly increase with the increasing of the turbulence speed.

1. Introduction

Aircraft and aerospace vehicle often suffer from severe environment with the combination of heat, vibration and noise during their service life. Turbulent boundary layer (TBL), as one of the most important sources of vibration, is an indispensable load which should be considered in the design of aircraft and aerospace structures [1-5]. The coupled effect between structure and acoustic may amplify vibration of structure and equipment inside the vehicle, which will further result in structural and functional failures [6, 7]. Therefore, the vibro-acoustic coupled analysis has been drawing an increasing attention in recent years. It is also necessary to consider the vibro-acoustic coupled effect to approach the real working conditions and achieve a more accurate prediction on structural response and acoustic radiation.

Acoustic tests are powerful supports for the development of the vibro-acoustic coupled analysis. However, the experimental investigation are restricted by the problems of the huge consumption, the long period and the limited conditions. With the increasing promotion of computer technology, numerical methods have been widely utilized to conduct the vibro-acoustic coupled analysis in recent years. The vibro-acoustic coupled analysis is generally carried out by using energy method [8-10] and discrete method [11-18]. The discrete methods are mainly based on the finite element method (FEM) and the boundary element method (BEM), such as FEM-FEM [11, 12, 19] and FEM-BEM [13-18]. In the FEM-FEM, both the structure and acoustic field are modeled by finite elements; when the acoustic field is modeled by 3-D solid elements, the computational cost is generally unacceptable. In the FEM-BEM, the structure and acoustic field are respectively simulated by finite elements and boundary elements, which can effectively reduce the degrees of freedom of the dynamic model in vibro-acoustic analysis. Therefore, the FEM-BEM method is usually superior to the FEM-FEM method for the vibro-acoustic analysis under bounded and unbounded acoustic excitations.

Vibro-acoustic analysis is usually conducted by using coupled or uncoupled approaches. In the uncoupled approach [12-14, 16, 18-20], the interaction between the structural and the acoustic is very weak and may be neglected. In this way, only one-way interaction is considered, and yields two types of dynamic problems for the uncoupled vibro-acoustic system. In the first type, the structural components are regarded as independent of the external acoustic excitations and the vibrations of the structural components generate acoustic pressures; In the second type, the acoustic components act as independent force excitations on the structural components. The distributions of the pressure caused by the acoustic waves along the fluid-structure interfaces generate vibrations in the structural components. Considering only a one-way interaction between the structural and acoustic components is a reasonable assumption for many vibro-acoustic problems, especially when an elastic structure with a high stiffness is surrounded by a low density fluid. In the coupled approaches [11, 15, 17, 20], the interaction between the structural and the acoustic components is no longer negligible and all components must be regarded as parts of one coupled system, instead of considering the structural components as independent excitations for the acoustic components or vice versa. Strong coupling effects may occur, for instance, when an elastic structure is submerged in a high-density fluid, or when a thin or lightweight structure contacts with a low-density fluid, etc.

Engineering structures are often subjected to uncorrelated and correlated random dynamic loads in time and/or space domains. In most cases, these excitations are assumed as uncorrelated which may result in inaccurate of structural or acoustic responses. It is necessary to develop appropriate methods to simulate correlated excitation effectively. Spatial correlation representing the level of interplay of excitation at different locations, which can be expressed by cross power spectral density functions in frequency domain. The distribution of TBL fluctuating wall pressure considering spatially correlation is usually obtained in three ways: experimental tests [9, 10], computational fluid dynamics (CFD) [21] and empirical formulations [22, 23]. Experimental tests can give exact distribution of the TBL fluctuating wall pressure. However, they are restricted by the problems of huge consume and limited conditions. CFD can also give the exact distribution of TBL, but this method requires a large amount of calculation which is very time consuming and is not conducive for complex structures. The empirical formulations fitted by experimental test data are widely used due to its simple practicality. Some patterns are often adopted, such as the Corcos model [22] and the Smol’yakov and Tkachenko model [23], et al.

In most of the previous works, the vibro-acoustic coupled analysis under correlated TBL excitation was generally limited to systems with a small number of DOFs. For complex structures under correlated TBL excitation, the vibro-acoustic coupled analysis was not deeply investigated. In order to study the influence of correlation on response and to obtain more accurate response, an algorithm that integrates FEM, BEM, and an acquisition method of excitation correlation is proposed to conduct the vibro-acoustic coupled analysis under correlated TBL. The outline of the work is as follows: in Section 2, the theory of vibro-acoustic coupled analysis under correlated TBL is firstly addressed; Then, a simply supported panel excited by correlated TBL is presented to validate the proposed algorithm in Section 3; In Section 4, the proposed method is applied to a stiffened panel and the effect of vibro-acoustic coupling, correlation of the excitation, the speed and thickness of turbulence on the structural and acoustic responses are studied. Finally, conclusions will be drawn in the last Section.

2. Vibro-acoustic coupled analysis excited by correlated TBL

2.1. Vibro-acoustic coupled analysis based on FEM-BEM

In this work, an algorithm that integrates finite element method (FEM), boundary element method (BEM), and an acquisition method of excitation correlation is adopted to carry out the vibro-acoustic coupled analysis under correlated TBL.

2.1.1. Finite element method

A time-invariant linear second-order system subjected to a forcing function can be written as:

1

(K_{s} + j ω C_{s} - ω^{2} M_{s}) u_{s} = F_{s},

where, $u_{s}$ is the nodal displacement vector, $ω$ is the circular frequency, $M_{s}$ , $C_{s}$ and $K_{s}$ are mass, damping and stiffness matrix of the structure, $F_{s}$ is the nodal forcing vector and the $j$ is the imaginary unit. The subscript “ $s$ ” denotes the structure.

The acoustic pressure difference between both sides of the structure along the acoustic-structure coupled interface can be regarded as an additional normal load. As a consequence, the additional load produced by the acoustic pressure difference should be added to the structural finite element model, yields:

2

(K_{s} + j ω C_{s} - ω^{2} M_{s}) u_{i} + L_{c} a_{i} = F_{s},

where, $a_{i}$ is the IBEM acoustic variables, $L_{c}$ is the acoustic-structure coupling matrix and can be expressed as:

3

L_{c} = - \sum_{e = 1}^{n_{s e}} (\int_{Ω_{s e}} N_{s}^{T} n^{e} N_{a} d Ω),

in which $n_{s e}$ is the number of structural finite elements, $Ω_{s e}$ is the area of the acoustic-structure coupled interface, $n^{e}$ represents the unit normal vector of structural finite elements, $N_{s}$ and $N_{a}$ are the shape function of structure and acoustic, respectively.

2.1.2. Boundary element method

Assuming the air is ideal gas, the Helmholtz equation can be expressed as:

4

\nabla^{2} p + k^{2} p = - j ρ_{0} ω q,

where, $p$ is acoustic pressure, $ρ_{0}$ is the density of the air, $k = ω / c$ is the acoustic wavenumber, $c$ is the speed of sound and $q$ is unit volume.

The Green’s kernel function $G (r, r_{a})$ represents the free-field pressure in point $r$ excited by an acoustic point source at $r_{a}$ , which satisfies the Helmholtz equation:

5

\nabla^{2} G (r, r_{a}) + k^{2} G (r, r_{a}) = - δ (r, r_{a}) .

In the three dimensional space, the Green’s kernel function is:

6

G (r, r_{a}) = \frac{\exp (- j k |r - r_{a}|)}{4 π |r - r_{a}|} .

In an interior/exterior coupled acoustic problem, there are two domains of air: a bounded domain which is interior to the closed boundary surface and an unbounded domain which is exterior to this boundary surface. Based on the definition of the boundary surface normal direction $n$ having a negative orientation into the unbounded air domain, the pressure and normal pressure gradient distributions along the positive and negative side of the boundary surface are denoted as $p^{-} (r_{a})$ , $p^{+} (r_{a})$ and $\partial p^{-} ({\vec{r}}_{a}) / \partial n$ , $\partial p^{+} ({\vec{r}}_{a}) / \partial n$ , respectively.

Based on the Green’s kernel function $G (r, r_{a})$ , the pressure distribution function $p (r_{a})$ and the second Green formulation, a general indirect boundary integral formulation can be obtained as:

7

p (r) = \int_{Ω_{a}} [μ (r_{a}) \frac{\partial G (r, r_{a})}{\partial n} - σ (r_{a}) G (r, r_{a})] d Ω (r_{a}), (r \in V | Ω_{a}),

where the single layer potential $σ (r_{a}) = \partial p^{+} (r_{a}) / \partial n - \partial p^{-} (r_{a}) / \partial n$ is the difference of normal pressure gradient between both sides of the boundary surface $Ω_{a}$ which can be regarded as a distribution of monopole sources on the boundary surface; the double layer potential $μ (r_{a}) = p (r_{a}^{+}) - p (r_{a}^{-})$ is the pressure difference between both sides of the boundary surface $Ω_{a}$ and represents a distribution of dipole sources on the boundary surface.

The indirect boundary element equation can be obtained by discretizing the acoustic boundary surface $Ω_{a}$ and expressing the boundary variables by boundary element node variables as follows:

8

D a_{i} = F_{a 1},

where $D$ is the IBEM influence matrix, and $F_{a 1}$ is the acoustic load along with the acoustic boundary surface $Ω_{a}$ .

Similar to the treatment of acoustic loading in FEM, the influence of force loading on acoustics can also be regarded as an additional external load. As a consequence, the additional load can be added to the acoustic boundary element model, yields:

9

D a_{i} = F_{a 1} + F_{c},

where, the coupling force matrix $F_{c}$ is expressed as:

10

F_{c} = - ρ_{0} ω^{2} L_{c}^{T} u_{i} - ρ_{0} ω^{2} \sum_{e = 1}^{n_{s e}} (\int_{Ω_{s e}} N_{a}^{T} n^{e} N_{a} {\bar{u}}_{i} d Ω) .

2.1.3. FEM-BEM method

Combining the modified structure finite element model as Eq. (2) and the modified acoustic boundary element model as Eq. (9), simultaneous equation of the coupled FEM-IBEM model is obtained as:

11

[\begin{matrix} K_{s} + j ω C_{s} - ω^{2} M & L_{c} \\ ρ_{0} ω^{2} L_{c}^{T} & D \end{matrix}] \{\begin{array}{l} u_{i} \\ a_{i} \end{array}\} = \{\begin{array}{l} F_{s} \\ F_{a} \end{array}\},

where:

12

F_{a} = - ρ_{0} ω^{2} \sum_{e = 1}^{n_{s e}} (\int_{Ω_{s e}} N_{a}^{T} n^{e} N_{a} {\bar{u}}_{i} d Ω) .

2.2. Power spectral density and correlation of the TBL excitation

Vibration and noise generated by the TBL has been and continues to be of interest in many engineering applications. To estimate the structural and acoustic response due to the TBL excitation, the nature of the TBL on the structure should be ascertained [24]. Measurements have shown that the TBL can be seen as a stationary and homogeneous random process. The power spectral density (PSD) of the TBL is usually obtained through wind tunnel scale model tests. The definition of auto PSD function of TBL is used from the tests or empirical formulation. In this work, the auto PSD of TBL is given by a test formulation as shown in Eq. (13) which is obtained by a TBL excitation with wind tunnel tests [8]. The auto PSD of TBL can also be replaced with any other expressions. However, the change of spectra will not affect the proposed methodology:

13

\frac{S_{F_{i} F_{i}}}{ρ^{2} h U_{0}^{3}} = \{\begin{array}{l} 0.0004 x^{- 0.66}, \\ 0.0012, \\ 0.0001 x^{- 2.2}, \\ 24.5 x^{- 9.1}, \end{array} \begin{array}{l} 0.06 \leq x \leq 0.17, \\ 0.17 \leq x \leq 0.32, \\ 0.32 \leq x \leq 6.0, \\ x \geq 6.0, \end{array}

where $x = ω h / U_{0}$ , $ω$ is the circular frequency in rad/sec, $h$ is the fence height in the experiment conducted by Han and Bernhard [8], $U_{0}$ is the free stream velocity, $ρ$ is the density of air.

The cross PSD of TBL is usually used to obtained the correlation of TBL in time and spatial domains. The Corcos model [22] is one of the classical models for describing cross correlation of the TBL. Corcos assumed that the longitudinal and lateral correlations can be presented as an exponentially decaying oscillating function in the flow direction and a simple exponentially decaying function in the cross flow direction, respectively, as follows:

14

S_{F_{i} F_{l}} (ξ_{1}, ξ_{2}, ω) = S_{F_{i} F_{i}} e^{- γ_{1} |\frac{ω ξ_{1}}{U_{c}}|} e^{- γ_{2} |\frac{ω ξ_{2}}{U_{c}}|} e^{- j \frac{ω ξ_{1}}{U_{c}}},

where $ξ_{1}$ and $ξ_{2}$ are the separation distances in the streamwise and spanwise directions; $γ_{1}$ and $γ_{2}$ are the decay rates; $U_{c}$ is turbulent convection speed, $U_{c} =$ 0.65 $U_{0}$ , $U_{0}$ is the mean flow velocity. The model originally developed for TBL over flat plates, is widely used for various flows because its mathematical simplicity. However, the use of this model provides satisfactory results only when the stream wise wave number $k$ is in the neighborhood of the convective wave number $ω / U_{c}$ . When $k$ is in the subconvective range, the Corcos model tends to over predict the result significantly.

For the purpose of comparative analysis, another cross PSD function model of TBL is generated by using Smol’yakov and Tkachenko model[23] (ST model). Smol’yakov and Tkachenko measured cross spectral densities as a function of spatial separation and boundary layer thickness, and fitted exponential curves to their results. Rather than using distinct lateral and longitudinal separations like the Corcos model, the ST model used a combined correlation and used Fourier transforms from. In the ST model, the influence of energy convective and boundary layer displacement thickness can be considered. It is found that the ST model can improve the accuracy in the low wavenumber levels over the Corcos model, but still higher than experimental data. Therefore, a correction factor is added to bring the model into agreement with experimental values as follows [23]:

15

S_{F_{i} F_{l}} (ξ_{1}, ξ_{2}, ω) = S_{F_{i} F_{i}} h (ω) [|γ_{0} (ξ_{1}, ξ_{2}, ω)| e^{j (\frac{ω ξ_{1}}{U_{c}})} - Δ γ (ξ_{1}, ξ_{2}, ω)],

where:

h (ω) = {[1 - \frac{0.153 A (1 + A^{2})}{\sqrt{(0.2 + A^{2}) (1.025 + A^{2})}}]}^{- 1},

|γ_{0} (ξ_{1}, ξ_{2}, ω)| = e x p (- \sqrt{{(\frac{A ω ξ_{1}}{U_{c}})}^{2} + {(\frac{6.45 A ω ξ_{2}}{U_{c}})}^{2}}),

Δ γ (ξ_{1}, ξ_{2}, ω) = B ∙ e x p (- \frac{0.9975 (1 + A^{2}) \sqrt{0.02 + A^{2}}}{1.025 + A^{2}} \sqrt{{(\frac{ω ξ_{1}}{U_{c}})}^{2} + {(\frac{ω ξ_{2}}{U_{c}})}^{2}})

∙ e x p (j \frac{1 + A^{2}}{1.025 + A^{2}} \frac{ω ξ_{1}}{U_{c}}),

B = \frac{0.153 A \sqrt{1 + A^{2}}}{\sqrt{(0.02 + A^{2}) (1.025 + A^{2})}}, A = 0.124 \sqrt{1 - \frac{0.2}{\bar{ω}} + {(\frac{0.2}{\bar{ω}})}^{2}}, \bar{ω} = \frac{ω δ}{U_{0}} .

2.3. Vibro-acoustic coupled response analysis excited by correlated TBL

When multiple correlated random excitations are applied to the structure, the cross PSD function is generally adopted to obtain the correlation between different excitations. The PSD of the structural or acoustic response $S_{p p}$ can be calculated as follows:

16

S_{p p} = H^{*} S_{F_{i} F_{l}} H^{T},

where $H$ is the transfer matrix of vibro-acoustic coupled function, which can be obtained by applying unit load on Eq. (11). $H^{*}$ is the conjugate matrix of $H$ . The expression of $H$ is as follows:

17

H_{d r} = [\begin{array}{l} H_{11} & \cdot \cdot \cdot & H_{1 i} & \cdot \cdot \cdot & H_{1 I} \\ ⋮ & ⋮ & ⋮ \\ H_{k 1} & \cdot \cdot \cdot & H_{k i} & \cdot \cdot \cdot & H_{k I} \\ ⋮ & ⋮ & ⋮ \\ H_{K 1} & \cdot \cdot \cdot & H_{K i} & \cdot \cdot \cdot & H_{K I} \end{array}],

where $K$ and $I$ are the total number of data recovery points and total number of locations where an external excitation is applied on the vibro-acoustic system, respectively. $S_{F_{i} F_{l}}$ is the PSD of excitation and can be expressed as follows:

18

S_{F_{i} F_{l}} = [\begin{array}{l} S_{F_{1} F_{1}} & \cdot \cdot \cdot & S_{F_{1} F_{l}} & \cdot \cdot \cdot & S_{F_{1} F_{I}} \\ ⋮ & ⋮ & ⋮ \\ S_{F_{i} F_{1}} & \cdot \cdot \cdot & S_{F_{i} F_{l}} & \cdot \cdot \cdot & S_{F_{i} F_{I}} \\ ⋮ & ⋮ & ⋮ \\ S_{F_{I} F_{1}} & \cdot \cdot \cdot & S_{F_{I} F_{l}} & \cdot \cdot \cdot & S_{F_{I} F_{I}} \end{array}] .

2.4. Implementation procedure for vibro-acoustic coupled analysis

An algorithm is proposed to carry out the vibro-acoustic coupled analysis under TBL that are correlated both in time and spatial domains. The implementation procedure is as follows:

(1) Creat the vibro-acoustic model based on the finite element and boundary element models;

(2) Divide the panel into $i$ ( $i =$ 2, 4, 6,…, $n$ ) subpanels in order to capture the correlation of the excitation;

(3) Apply unit excitation on each subpanels $P_{i}$ and the vibro-acoustic coupled transfer function matrix $H$ can be obtained;

(4) The auto PSD can be obtained by using Eq. (13), and the cross PSD can be obtained by discretizing the cross PSD of Corcos in Eq. (14) or ST in Eq. (15);

(5) The vibro-acoustic coupled analysis is carried out by using FEM-BEM. Then the PSD and RMS of responses are obtained;

(6) If the RMS of response due to $n$ subpanels tends to convergence, then the number of subpanels $n$ is selected for the following vibro-acoustic coupled analysis;

(7) If the RMS of response due to $n$ subpanels doesn’t converge, then return to step (1) and the panel is divided into $m$ ( $m > n$ ) subpanels.

In order to study the influence of the correlation on the response of vibro-acoustic coupled system, the vibro-acoustic coupled analysis is carried out in three cases based on the correlation of TBL: (1) perfectly correlated case. In this case, the excitations are perfectly correlated and the cross correlation are one; (2) partially correlated case based on the Corcos or ST models. The correlation is obtained by using the Corcos or ST models; (3) uncorrelated case. The excitations in each subpanels are independent, and only the auto PSD of excitation is considered. The cross correlation is zero.

3. Validation of the proposed algorithm

In order to validate the accuracy of the proposed algorithm, the algorithm is applied to a simply supported aluminum rectangular panel for the vibro-acoustic coupled analysis under correlated TBL, as show in Fig. 1. The dimensions and the material properties of the panel are given in Table 1. The vibro-acoustic coupled model is established based on the structural finite element method and acoustic boundary element method. The structural FEM are modeled by using 30×30 four-noded quadrilateral linear shell elements. The acoustic BEM is also modeled by four noded quadrilateral elements with the same size to the structural finite element model. The panel is assumed to be vibrating in air whole. The parameters of the TBL excitation used in this manuscript are given in Table 2.

Fig. 1The panel under correlated TBL excitation

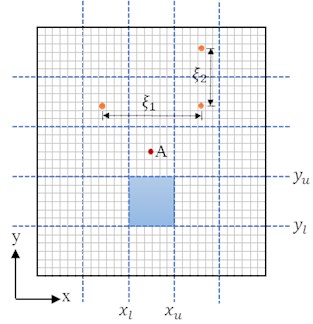
For the vibro-acoustic coupled analysis of complex structure due to correlated excitation, the amount of computing data would be very large when the correlation in both time and spatial domains for all element nodes is considered. To capture the spatial correlation efficiently, the panel is divided into several subpanels, as shown in Fig. 1; e.g. $x_{l}$ , $x_{u}$ , $y_{l}$ , $y_{u}$ are the bounds of a subpanel. Subscript $l$ and $u$ on $x$ and $y$ are used for the lower and upper bounds in the $x$ and $y$ directions, respectively. However, the process of partitioning the domain cannot be completely arbitrary. The division of subpanels must be fine enough in order to obtain accuracy results. In order to obtain an optimal number of subpanels, the panel is divided into different subpanels using 2×2 to 6×6 grids. The PSD of the accelerations at point A with different number of subpanels under partially correlated TBL (based on Corcos and ST models) are shown in Fig. 2. The corresponding root mean squares (RMS) of the accelerations with the number of subpanels are plotted in Fig. 3. Results show that the PSD and RMS of accelerations converge to a relatively stable value with the increase of the subpanels’ number. Therefore, the number of subpanels 6×6 is enough and reasonable for the following vibro-acoustic coupled analysis based on a combination of computational efficiency and sufficient accuracy. We also notice that the structural responses have not a consistent decrease with the increment of subpanels, for example, the response where the panel is divided into 3×3 subpanels is larger than that when the panel is divided into 2×2 subpanels. This is due to the point A is in the symmetry center of the panel, and when the panel is divided into 2×2 equal subpanels, the contribution of the structural anti-symmetric modes to the response are not being considered.

Table 1The dimensions and material properties of the panel

Parameters	Values
Length of the panel	460 mm
Width of the panel	360 mm
Thickness of the panel	4.8 mm
Young’s modulus	73000 MPa
Density	2700 kg/m³
Poisson’s ratio	0.33
Damping loss factor	2.0 %

Table 2Numerical values of the parameters used in the TBL model

Parameters	Values
Free stream velocity ( $U_{0}$ )	35.75 m/s
Density of air ( $ρ$ )	1.22 kg/m³
Speed of air ( $c$ )	340 m/s
Decay rate, streamwise ( $γ_{1}$ )	0.16
Decay rate, spanwise ( $γ_{2}$ )	0.46
Fence height in the experiment ( $h$ )	0.0254 m

Fig. 2PSD of the accelerations with different number of subpanels under partially correlated TBL based on Corcos and ST models

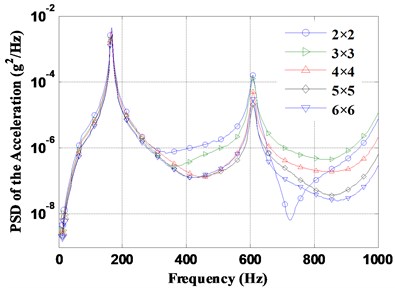
a) Results under partially correlated TBL based on Corcos model

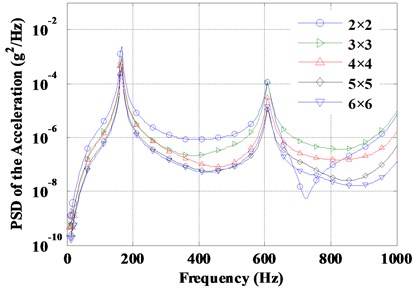
b) Results under partially correlated TBL based on ST model

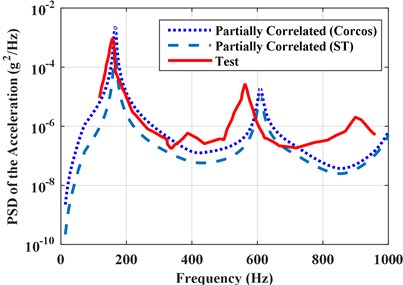
The PSD of accelerations at point A under partially correlated TBL excitations based on Corcos and ST models are compared with the experimental test results [10], as shown in Fig. 4. The results using proposed algorithm have an agreement with the test result, which means that the proposed algorithm in this work are correct and valid. It should also be noticed that the second frequencies of the response peaks have a slight difference with the test results. This is because the boundary condition in test is hard to reach the ideal simple supported boundary condition, which will result in a change of natural frequencies.

Fig. 3RMS of the accelerations with different number of subpanels under partially correlated TBL

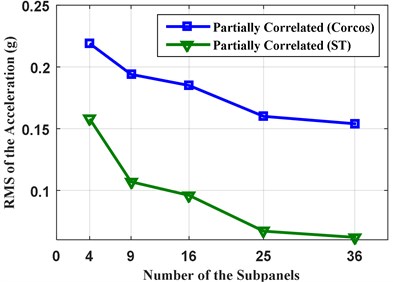
Fig. 4PSD of the accelerations under partially correlated TBL

4. Numerical simulations

To further check the general applicability of the proposed algorithm, a stiffened panel, as shown in Fig. 5, is used to carry out the vibro-acoustic coupled analysis. Stiffened panels are widely used in engineering structures, such as bridges, buildings, automobiles, vehicle and vessels, etc. due to their very high stiffness to weight ratio [25]. Stiffened panel usually consists of a basic structure and local reinforcement elements called stiffeners to improve the static and dynamic characteristics of the structure. Stiffened panel represents the case of fuselage, submarine and ship panels where the turbulent boundary layer (TBL) is acting on the outside surface of the panel. The stiffened panel dimensions and material properties are given in Table 3. The point A (0.24, 0.97, 0) and point B (0.58, 0.58, 0.6) are selected for monitoring the structural and acoustic response, respectively.

The vibro-acoustic coupled model of the stiffened panel is also established based on the structural FEM and acoustic BEM. In order to ensure the accuracy of the established FEM model, a convergence study has been carried out using NASTRAN where four noded quadrilateral elements (CQUAD4 in Nastran) are used. Table 4 shows that the first 8 natural frequencies of the stiffened panel are obtained by different number of finite elements. When the number of finite elements is greater than 30×30, converged results can be obtained. Based on a combination of computational efficiency and sufficient accuracy, the optimum number of finite elements 30×30 is determined for subsequent analysis. Then the convergence of the response due to number of division of subpanels is also studied. In a similar fashion as in Section 3, the number of subpanels 5×5 is sufficient to carry out the following vibro-acoustic coupled analysis.

Fig. 5The stiffened panel under correlated TBL

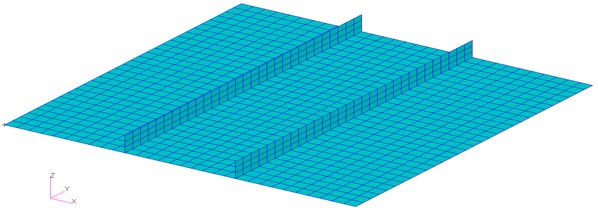
Table 3The dimensions and material properties of the stiffened panel

Parameters	Values
Length of the panel	1.1684 m
Width of the panel	1.1684 m
Thickness of the panel	0.005 m
Height of the stiffener	0.0577 m
Thickness of the stiffener	0.003 m
Distance of the stiffener away from panel edge	0.400 m
Young’s modulus	73.08×10⁹ N/m²
Poisson’s ratio	0.33
Density	2.70×10³ kg/m³
Damping loss factor	0.02

Table 4The first 8 natural frequencies of the stiffened panel (Hz)

Mesh size	(2, 1)	(2, 1)	(3, 1)	(3, 2)	(4, 2)	(3, 3)	(4, 3)	(3, 3)
12×12	50.59	51.28	55.90	67.38	74.87	91.56	97.66	103.36
18×18	50.63	51.35	55.99	68.52	75.69	94.04	99.97	103.08
24×24	50.67	51.40	56.06	69.03	76.16	95.11	101.05	103.43
30×30	50.67	51.40	56.07	69.28	76.40	95.65	101.62	103.65
36×36	50.71	51.71	56.12	69.48	76.62	96.06	102.06

4.1. Effect of the vibro-acoustic coupling

To explore the effect of vibro-acoustic coupling on the structure, the analyses of natural characteristics and dynamic responses in both coupled and uncoupled conditions are carried out.

Table 5 shows the first ten coupled and uncoupled natural frequencies of the stiffened panel. It shows that the natural frequencies slightly decrease as considering the vibro-acoustic coupled effect. However, the vibro-acoustic coupling has little effect on the model shapes. This is mainly due to the influence of vibro-acoustic coupling on structure can be regard as an air additional mass effect, which has a negative effect on the natural frequencies of structure.

Table 5The first ten coupled and uncoupled natural frequencies of the stiffened panel (Hz)

Modal indices	Uncoupled	Coupled
(2, 1)	50.67	49.35
(2, 1)	51.40	49.39
(3, 1)	56.07	54.65
(3, 2)	69.28	68.18
(4, 2)	76.40	75.03
(3, 3)	95.65	94.41
(4, 3)	101.62	100.21
(3, 2)	103.65	101.50
(4, 1)	107.97	106.85
(3, 3)	128.95	127.12

The effect of vibro-acoustic coupling on structural and acoustic responses is also studied. The coupled PSD and RMS of the acceleration at point A and pressures at point B are obtained under the three different types of excitations: perfectly correlated, partially correlated, uncorrelated, and compared with the uncoupled results, as shown in Figs. 6 and 7. The corresponding RMS of the structural and acoustic responses are shown in Table 6. Results show that the vibro-acoustic coupled effect has a significant influence on the structural response, but has little influence on the acoustic response. The coupled effect results in the decrease of the structural response under perfectly correlated excitation, but increase of the structural response under partially correlated and uncorrelated excitations. This illustrates the vibro-acoustic coupled effect on structural response is related to the correlation of excitation. When the excitations are considered to be partially correlated and uncorrelated, the more contribution of air to the structural response is increased due to the vibro-acoustic coupling. In other words, the vibro-acoustic coupled effect can result in the increase of structural response because the excitations are partially correlated in many real-life vibration problems. Moreover, the influence of coupled effect on structural response is more obvious for the thin-shell structures. Therefore, it is very important to consider the vibro-acoustic coupling because the structure is actually “surrounded” by the air, which can more actually reflect the dynamic characteristics of the vibro-acoustic system.

Fig. 6Coupled and uncoupled PSD of the accelerations under perfectly correlated, partially correlated and uncorrelated excitations

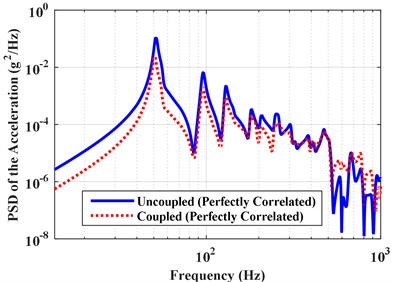
a) Results under perfectly correlated TBL

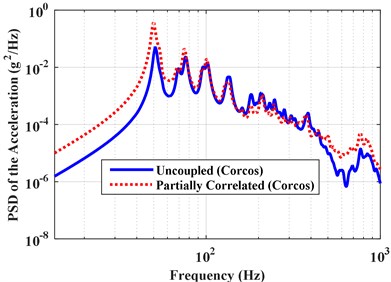
b) Results under partially correlated TBL (Corcos model)

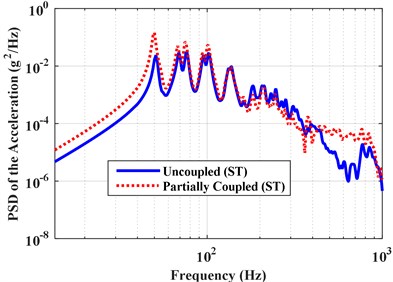
c) Results under partially correlated TBL (ST model)

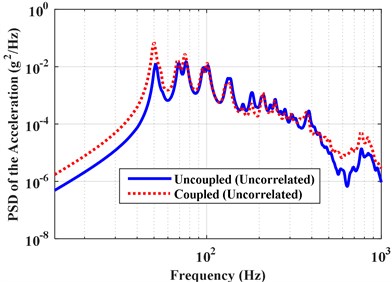
d) Results uncorrelated TBL

Fig. 7Coupled and uncoupled PSD of the pressures under perfectly correlated, partially correlated and uncorrelated excitations

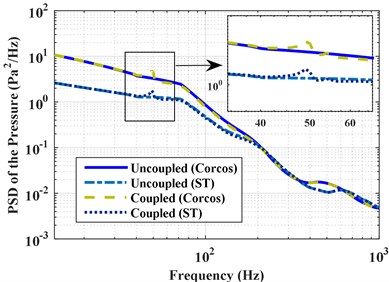
a) Results under partially correlated excitations

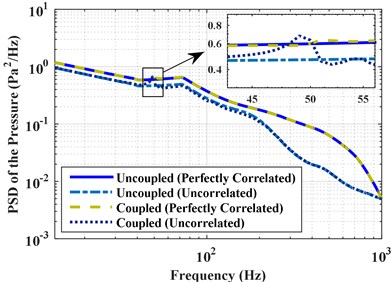
b) Results under perfectly correlated and uncorrelated excitations

Table 6Coupled and uncoupled RMS of the acceleration and pressure for perfectly correlated, partially correlated and uncorrelated excitations

Correlation	Structural RMS (g)		Acoustic RMS (Pa)
Correlation	Uncoupled	Coupled	Uncoupled	Coupled
Perfectly correlated	0.70	0.36	11.13	11.13
Partial correlated (Corcos)	0.80	1.36	18.83	18.77
Partial correlated (ST)	0.96	1.30	12.01	11.93
Uncorrelated	0.68	0.85	8.70	8.59

4.2. Effect of the correlation of excitation

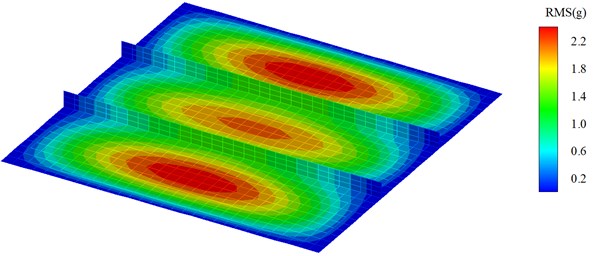
The effect of correlation among random excitations on structural and acoustic responses is also carried out. The responses are also obtained using the three different types of excitations: the perfectly correlated, the partially correlated and the uncorrelated. The PSD and RMS of the accelerations at point A and pressures at point B due to the three excitations are obtained and shown in Fig. 8 and Table 6, respectively. The RMS contour of the stiffened panel under partially correlated excitation based on Corcos model is shown in Fig. 9. Results show that the structural and acoustic responses under partially correlated excitation are larger than that under perfectly correlated excitation. The increase of the response is due to the phase difference between different TBL excitation locations of the system. When considering the partially spatial correlation of the TBL excitation, the phase difference which has a positive effect on the response is taken into account. However, when the TBL are considered into perfectly correlated excitations, the excitations ignore the positive factor produced by phase difference. It is also noticed that some new response’ peaks appear when the excitation is considered to be partially correlated or uncorrelated. When the excitation is partially correlated or uncorrelated, more natural frequencies of the vibro-acoustic coupled system are aroused which may also result in an increase of the response.

Mostly, the vibro-acoustic coupled analysis of complex structure under correlated random excitation is carried out either by considering the excitation as perfectly correlated or uncorrelated. However, if the correlation of excitation is ignored, the response will be smaller than the actual conditions. Therefore, it is helpful to consider the correlation of random excitations in the structural optimization or fatigue calculations.

Fig. 8PSD of the accelerations and pressures under perfectly correlated, partially correlated, and uncorrelated excitations

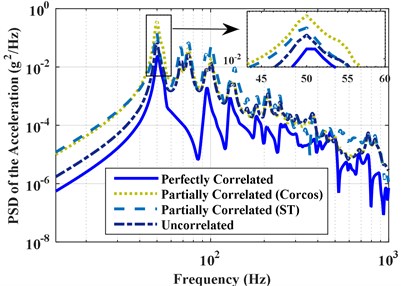
a) PSD of the accelerations

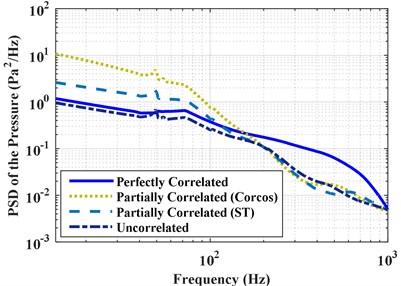
b) PSD of the pressures

4.3. Effect of the turbulence

The effect of turbulence speed and thickness on the response is further studied in this section. First, the vibro-acoustic coupled analysis is conducted under different turbulence speeds: 20.0 m/s, 35.8 m/s, 50.0 m/s and 70.0 m/s. Fig. 10 gives the PSD of the accelerations and pressures with different turbulence speeds under partially correlated TBL. The RMS of the accelerations and pressures with different flow speeds for the three types of excitations (perfectly correlated, partially correlated, and uncorrelated excitations) are shown in Fig. 11, respectively. The PSD and RMS of the responses increase with an increase of turbulence speed, but the trend of the responses is almost same. This is mainly due to the auto PSD of excitations increase with the increasing of turbulence speed, as noted in Fig. 12. When conducting the matrix multiplication in Eq. (16), the increasing of excitation PSD causes a positive effect on the PSD of response. The differences among the responses under the three different excitations rapidly increase with the increment in turbulence speed. As one can see from Fig. 11, the difference of responses due to the three excitations is very small at speed 20 m/s, but the difference is very obvious at speed 70 m/s. This is due to that the influence of spatial correlation on the responses is small in the low Mach number of turbulent boundary layer flow. However, the spatial correlation has a growing influence on the responses with the increasing of flow speed.

Fig. 9RMS contour of the acceleration under partially correlated excitation

Next, the vibro-acoustic coupled response is obtained under different TBL turbulence thicknesses: 0.010 m, 0.045 m, 0.060 m, and 0.100 m, and the turbulence speed is fixed to 35.8 m/s. The PSD and RMS of the accelerations and pressures with different turbulence thicknesses under partially correlated TBL based on ST model are shown in Figs. 13 and 14, respectively. The PSD and RMS of the responses increase with the increase of turbulence thickness. This is because the energy convective increase with the increase of turbulence thickness, which result an incensement of spatial correlation.

Fig. 10PSD of the accelerations and pressures with different turbulence speeds under partially correlated excitations (Corcos model)

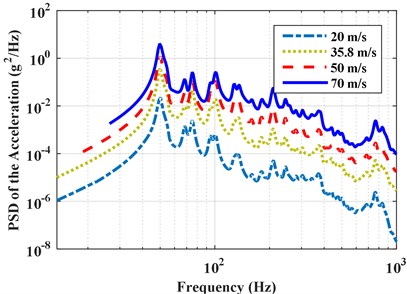
a) PSD of the accelerations with different turbulence speeds

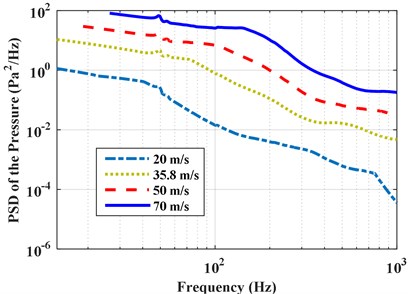
b) PSD of the pressures with different turbulence speeds

Fig. 11RMS of the accelerations and pressures with different turbulence speeds under perfectly correlated, partially correlated, and uncorrelated excitations

RMS of the accelerations and pressures with different turbulence speeds under perfectly correlated, partially correlated, and uncorrelated excitations

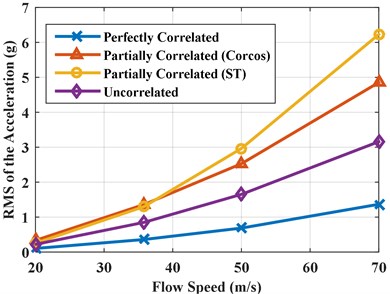
a) RMS of the accelerations with different turbulence speeds

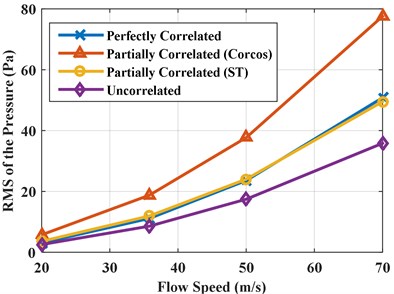
b) RMS of the pressures with different turbulence speeds

Fig. 12Auto PSD of pressures with different turbulence speeds

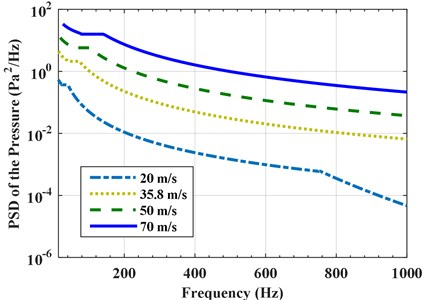
Fig. 13PSD of accelerations and pressures with different TBL thicknesses

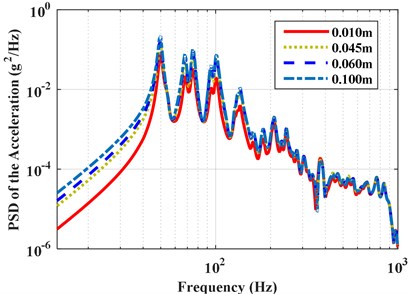
a) PSD of the accelerations with different TBL thicknesses

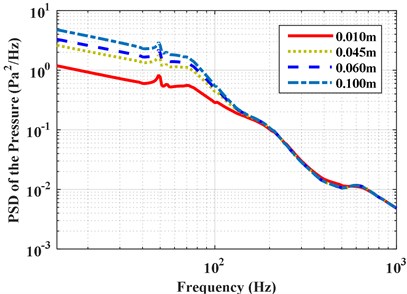
b) PSD of the pressures with different TBL thicknesses

Fig. 14RMS of accelerations and pressures with different TBL thicknesses

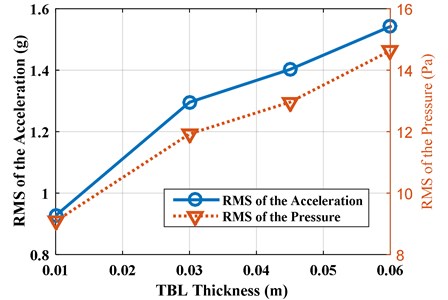
5. Conclusions

A methodology is presented wherein the finite element method (FEM), the boundary element method (BEM) and an acquisition method of excitation correlation are integrated to conduct the vibro-acoustic coupled analysis under TBL excitation correlated in time and spatial domains. The Corcos/ST PSD model are adopted to obtain the spatial correlation of TBL. A divisional method of structure is proposed to capture the spatial correlation of excitation, which has a big advantage on the vibro-acoustic coupling analysis of complex structures.

A simply supported panel under correlated TBL is presented first to validate the proposed algorithm. To capture the spatial correlation efficiently, the panel is divided into several subpanels with the number of subpanels being determined by a convergence study. Second, the proposed algorithm is applied to a stiffened panel, and factors which may affect the vibro-acoustic coupled analysis, such as the vibro-acoustic coupling, the correlation of excitation and the turbulence speed and thickness are also discussed. To investigate the influence of correlation on vibro-acoustic coupled system, the vibro-acoustic coupled analysis is carried out with three types of excitations: perfectly correlated, partially correlated based on Corcos and ST models and uncorrelated TBL. Results show that the proposed method is suitable for the vibro-acoustic coupled analysis of complex system under correlated random excitations. Vibro-acoustic coupled effect can result in the decrease of natural frequencies and structural responses for perfectly correlated excitation, but increase of the structural response for partially correlated and uncorrelated excitations. However, the vibro-acoustic coupled has little effect on the acoustical responses. The structural and acoustic responses due to partial correlated excitations are larger than that due to perfectly correlated excitations, which results from the phase difference of the excitation. The structural and acoustical responses increase with the increment in turbulence speed and thickness. Moreover, the difference among the responses under the three different excitations rapidly increase with the increment of turbulence speed.

References

Graham W. R. Boundary layer induced noise in aircraft. Part I: the ﬂat plate model. Journal of Sound and Vibration, Vol. 192, Issue 1, 1996, p. 101-120.

Publisher
Graham W. R. Boundary layer induced noise in aircraft. Part II: the trimmed ﬂat plate model. Journal of Sound and Vibration, Vol. 192, Issue 1, 1996, p. 121-138.

Publisher
Liu B. L., Zhang H., Qian Z. C., Chang D. Q., Yan Q. Inﬂuence of stiffeners on plate vibration and radiated noise excited by turbulent boundary layers. Applied Acoustics, Vol. 80, 2014, p. 28-35.

Publisher
Liu B. L., Feng L. P., Nilsson A., Aversano M. Predicted and measured plate velocities induced by turbulent boundary layers. Journal of Sound and Vibration, Vol. 331, Issue 24, 2012, p. 5309-5325.

Publisher
Hambric S. A., Hwang Y. F., Bonness W. K. Vibrations of plates with clamped and free edges excited by low-speed turbulent boundary layer flow. Journal of Fluids and Structures, Vol. 19, Issue 1, 2004, p. 93-110.

Publisher
Li Y. B., Zhang P., Zou Y. J., Wu S. Q., Fei Q. G. Structural-acoustic coupling analysis of a bearing cylinder-skin structure under random base excitation. Journal of Astronautics, Vol. 36, Issue 2, 2015, p. 236-242.

Search CrossRef
Li Y. B., Zhang P., Wu, S. Q., Fei Q. G. Structural-acoustic coupling analysis of a composite stiffened panel in a thermal environment. Journal of Vibration Engineering, Vol. 28, Issue 4, 2015, p. 531-540.

Search CrossRef
Han F., Bernhard R. J., Mongeau L. G. Prediction of flow-induced structural vibration and sound radiation using energy flow analysis. Journal of Sound and Vibration, Vol. 227, Issue 4, 1999, p. 685-709.

Publisher
Heatwole C. M., Franchek M. A., Bernhard R. J. Robust feedback control of flow-induced structural radiation of sound. The Journal of the Acoustical Society of America, Vol. 102, Issue 2, 1997, p. 989-997.

Publisher
Heatwole C. M., Franchek M. A., Bernhard R. J. A robust feedback controller implementation for flow induced structural radiation of sound. Noise Conference, Seattle, Wash, Vol. 96, 1996, p. 357-362.

Search CrossRef
Abbes M. S., Bouaziz S., Chaar F. I., Maatar M., Haddar M. An acoustic-structural interaction modelling for the evaluation of a gearbox-radiated noise. International Journal of Mechanical Sciences, Vol. 50, Issue 3, 2008, p. 569-577.

Publisher
Pankaj J., Mulani S. B., Slemp W. C. H., Kapania R. K. Vibro-acoustic optimization of turbulent boundary layer excited panel with curvilinear stiffeners. Journal of Aircraft, Vol. 49, Issue 1, 2012, p. 52-65.

Publisher
Allen M. J., Vlahopoulos N. Integration of finite element and boundary element methods for calculating the radiated sound from a randomly excited structure. Computers and Structures, Vol. 77, Issue 2, 2000, p. 155-169.

Publisher
Allen M. J., Vlahopoulos N. Noise generated from a flexible and elastically supported structure subject to turbulent boundary layer flow excitation. Finite Elements in Analysis and Design, Vol. 37, Issue 9, 2001, p. 687-712.

Publisher
Seybert A. F., Wu T. W., Li W. L. A coupled FEM/BEM for fluid-structure interaction using Ritz vectors and eigenvectors. Journal of Vibration and Acoustics, Vol. 115, Issue 2, 1993, p. 152-158.

Publisher
Jeyaraj P. Vibro-acoustic behavior of an isotropic plate with arbitrarily varying thickness. European Journal of Mechanics – A/Solids, Vol. 29, Issue 6, 2010, p. 1088-1094.

Publisher
Vlahopoulos N., Vallance C., Stark R. D. Numerical approach for computing noise-induced vibration from launch environments. Journal of Spacecraft and Rockets, Vol. 35, Issue 3, 1998, p. 355-360.

Publisher
Buehrle R. D., Grosveld F. W. Vibro-Acoustic model validation for a curved honeycomb composite panel. 42nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Seattle, WA, 2001, p. 16-19.

Search CrossRef
Lakis A. A., Paidoussis M. P. Prediction of the response of a cylindrical shell to arbitrary or boundary-layer-induced random pressure fields. Journal of Sound and Vibration, Vol. 25, Issue 1, 1972, p. 1-27.

Publisher
Hekmati A., Ricot D., Druault P. Numerical synthesis of aeroacoustic wall pressure fields over a flat plate: generation, transmission and radiation analyses. Journal of Sound and Vibration, Vol. 332, Issue 13, 2013, p. 3163-3176.

Publisher
Rai M. M., Moin P. Direct numerical simulation of transition and turbulence in a spatially evolving boundary layer. Journal of Computational Physics, Vol. 109, Issue 2, 1993, p. 169-192.

Publisher
Corcos G. M. The structure of the turbulent pressure field in boundary-layer flows. Journal of Fluid Mechanics, Vol. 18, Issue 3, 1964, p. 353-378.

Publisher
Smal’yakov A. V., Tkachenko V. M., Wood J. S. Model of a field of pseudosonic turbulent wall pressures and experimental data. Soviet Physical Acoustics, Vol. 37, Issue 6, 1991, p. 627-631.

Search CrossRef
Nigam N. C., Narayanan S. Applications of Random Vibrations. Springer-Verlag, New York, 1994.

Search CrossRef
Li Y. B., Mulani S. B., Scott K. M. L., Kapania R. K., Wu S. Q., Fei Q. Q. Non-stationary random vibration analysis of multi degree systems using auto-covariance orthogonal decomposition. Journal of Sound and Vibration, Vol. 372, Issue 23, 2016, p. 147-167.

Publisher

Cited by

Vibro-acoustic modeling of the turbulent excited cavity-plate-exterior space coupled system

(2024)

Full-Frequency Vibroacoustic Modeling of a Ballistic Re-Entry Aeroshell and Validation through Diffuse Field Acoustic Testing

Maxence Claeys | Hélène Valle Canas | Benoit Alcoverro

(2022)

A formulation for turbulent-flow-induced vibration of elastic plates with general boundary conditions

Xiaoji Song | Guoyong Jin | Tiangui Ye | Saifeng Zhong

(2021)

About this article

Received

14 January 2016

Accepted

02 May 2016

Published

15 August 2016

SUBJECTS

Flow induced structural vibrations

DOI

https://doi.org/10.21595/jve.2016.16831

Keywords

vibro-acoustic coupled analysis

correlated excitation

turbulent boundary layer

FEM

BEM

Acknowledgements

The work described in this paper was supported by China Scholarship Council (CSC), a Graduate Research and Innovation Projects in Jiangsu Province (CXZZ13_0084), a Program for New Century Excellent Talents in University (NCET-11-0086), a Research Grant by the National Natural Science Foundation of China (11572086 and 11402052), the Jiangsu Natural Science Foundation (BK20140616), and the Fundamental Research Funds for the Central Universities.

Author Contributions

Yanbin Li conceived, preformed analysis and drafted the manuscript. Qingguo Fei conceived, revised the manuscript, and acted as corresponding author. Shaoqing Wu reviewed and revised the manuscript. Peng Zhang was involved in data analysis and interpretation. Dong Jiang revised and evaluated the manuscript. All authors have read and approved the final manuscript.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2021 04 07

Numerical simulation analysis of a PGR exterior body structure considering vibroacoustic characteristics

ShuE Ji, Yongmei Wang, Xigui Wang, Jiafu Ruan, Siyuan An, Baixue Fu

Research article

2020 11 30

Free vibration analysis of structural-acoustic coupled system using hybrid impedance and mobility approach

Amogh Nalawade, Veerabhadra Reddy S Y, Venkatesham B

Research article

2020 08 15

Experimental study on vibration characteristics of fluid-solid coupling cantilever thin aluminum plate

Ma Yinhanga, Jiang Hanyanga, Dai Meilingb, Yang Fujuna

Research article

2018 10 19

Parametric study of unsteady-flow-induced volute casing vibro-acoustics in a centrifugal fan

Jianhua Zhang, Wuli Chu, Yi Lv

Y. Li, Q. Fei, S. Wu, P. Zhang, and D. Jiang, “Vibro-acoustic coupled analysis excited by correlated turbulent boundary layer,” Journal of Vibroengineering, Vol. 18, No. 5, pp. 3225–3241, Aug. 2016, https://doi.org/10.21595/jve.2016.16831

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2016.16831
UR  - https://doi.org/10.21595/jve.2016.16831
TI  - Vibro-acoustic coupled analysis excited by correlated turbulent boundary layer
T2  - Journal of Vibroengineering
AU  - Fei, Qingguo
AU  - Li, Yanbin
AU  - Wu, Shaoqing
AU  - Zhang, Peng
AU  - Jiang, Dong
PY  - 2016
DA  - 2016/08/15
PB  - JVE International Ltd.
SP  - 3225-3241
IS  - 5
VL  - 18
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Fei_2016,
	doi = {10.21595/jve.2016.16831},
	url = {https://doi.org/10.21595/jve.2016.16831},
	year = 2016,
	month = {aug},
	publisher = {{JVE} International Ltd.},
	volume = {18},
	number = {5},
	pages = {3225--3241},
	author = {Qingguo Fei and Yanbin Li and Shaoqing Wu and Peng Zhang and Dong Jiang},
	title = {Vibro-acoustic coupled analysis excited by correlated turbulent boundary layer},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]Q. Fei, Y. Li, S. Wu, P. Zhang, and D. Jiang, “Vibro-acoustic coupled analysis excited by correlated turbulent boundary layer,” Journal of Vibroengineering, vol. 18, no. 5, pp. 3225–3241, Aug. 2016, doi: 10.21595/jve.2016.16831.

Copy IEEE

Copied to clipboard!

Fei, Qingguo, Yanbin Li, Shaoqing Wu, Peng Zhang, and Dong Jiang. “Vibro-Acoustic Coupled Analysis Excited by Correlated Turbulent Boundary Layer.” Journal of Vibroengineering 18, no. 5 (August 15, 2016): 3225–41. https://doi.org/10.21595/jve.2016.16831.

Copy Chicago

Copied to clipboard!

Vibro-acoustic coupled analysis excited by correlated turbulent boundary layer

Abstract

1. Introduction

2. Vibro-acoustic coupled analysis excited by correlated TBL

2.1. Vibro-acoustic coupled analysis based on FEM-BEM

2.1.1. Finite element method

2.1.2. Boundary element method

2.1.3. FEM-BEM method

2.2. Power spectral density and correlation of the TBL excitation

2.3. Vibro-acoustic coupled response analysis excited by correlated TBL

2.4. Implementation procedure for vibro-acoustic coupled analysis

3. Validation of the proposed algorithm

4. Numerical simulations

4.1. Effect of the vibro-acoustic coupling

4.2. Effect of the correlation of excitation

4.3. Effect of the turbulence

5. Conclusions

References

Cited by

About this article

Related Articles