Large amplitude free vibrations of simply supported moderately thick rectangular plates using coupled displacement field method

Bhaskar K, Krishna; Saheb K, Meera

doi:10.21595/jve.2016.16889

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 September 2016

Check for updates

Large amplitude free vibrations of simply supported moderately thick rectangular plates using coupled displacement field method

Krishna Bhaskar K¹

Meera Saheb K²

^{1, 2}University College of Engineering (A), JNTUK Kakinada, Andhra Pradesh, India

Corresponding Author:

Krishna Bhaskar K

Cite the article Download PDF

Downloads 1620

CrossRef Citations 1

Abstract

In this paper a novel method known as Coupled Displacement Field Method was proposed to evaluate the large amplitude free vibration behavior of the moderately thick rectangular plates with simply supported boundary conditions. Here a single term trigonometric admissible displacement field was assumed for one of the variables, say the total rotations (in both $X$ , $Y$ directions). With the help of the coupling equations, the spatial variation for the lateral displacement field is derived in terms of the total rotations, where the two independent variables problem becomes one. The coupled displacement field method makes use of the energy formulation which contains half the number of unknown independent coefficients, in the case of a rectangular plate, when compared to the conventional Rayleigh-Ritz method. Closed form expressions for the linear and nonlinear fundamental frequency parameters for the all edges simply supported moderately thick rectangular plates are derived. The numerical results obtained from the present formulation are validated with those obtained from the existing literature for the given moderately thick plates.

1. Introduction

Evaluation of free vibration behavior of a structure is an essential consideration in the design of a structure. Understanding the fundamental frequency parameters for moderately thick rectangular plates will be advantageous in the design of structural members at the initial design phase. The conventional energy methods provide an effective means in evaluating the fundamental frequency parameters of these structural members and the results obtained by these approaches will act as an upper limit for comparison.

The concept of coupled displacement field (CDF) which was successfully used in the finite element (FE) analysis and reported in the open literature. However much attention was not received in the continuum correlation of the Finite element analysis combined with the CDF in the past years except in the formulation presented by Zhou [1] where the two independent variables (transverse displacement and rotation) are integrated using coupling equation. The large amplitude free vibration behavior of uniform Timoshenko beams using CDF method was successfully demonstrated [2]. In this study, using CDF method the large amplitude free vibration behavior of uniform shear deformable moderately thick rectangular plates was studied and exact closed form solutions were obtained. For the thin plates the fundamental frequency parameter was evaluated in [3-10] for several configurations and boundary conditions. Nonlinear analysis of plates was evaluated by using finite element method [4, 13]. S. H. Hashemi et al. [11] used dimensionless equation of motion and solved the problem based on theory to study the transverse vibration behavior of thick rectangular plates. In Rayleigh-Ritz method we need to assume an n term admissible trial function for the total rotation and another n term admissible trial function for the transverse displacement for solving for solving free vibration analysis of Mindlin plate. This result in the vibration problems to have 2 $n$ unknown undetermined coefficients, in general and the use of the classical Rayleigh Ritz method [12, 14] contain 2n homogeneous simultaneous equations which are to be solved in order to obtain fundamental frequency parameter.

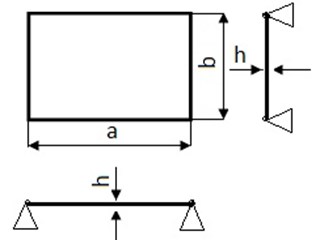
In this paper the independent fields for total rotation and the transverse displacement are coupled by using coupling equations, which are derived from static equilibrium equations in order to obtain static solution for shear deformable moderately thick rectangular plates. This methodology reduces the magnitude of the problem by reducing the number of unknown coefficients from 2n to n when compared with classical Rayleigh Ritz method. The practicality of CDF method is verified by solving the vibration problem considering uniform and isotropic moderately thick rectangular plates with all edges simply supported boundary conditions Fig. 1. The numerical results obtained by this method are compared with the results obtained from the finite element method [12] and other researchers. The comparison quantifies the effectiveness of the proposed CDF method.

Fig. 1Uniform all edges simply supported moderately thick rectangular plates

2. Coupled displacement field (CDF) method for plates

In this section the detailed procedure for evaluating fundamental linear frequency parameter of uniform all edges simply supported moderately thick rectangular plate based on CDF method is discussed. Here an admissible trial functions for $θ_{x}$ and $θ_{y}$ are assumed in the functional form which satisfy the boundary conditions and symmetric conditions for the fundamental mode as:

1

θ_{x} = α \frac{π}{a} c o s \frac{π x}{a} s i n \frac{π y}{b},

2

θ_{y} = α \frac{π}{b} s i n \frac{π x}{a} c o s \frac{π y}{b} .

The coupling equations for evaluating the transverse displacement distribution $w$ in $x$ and $y$ directions are given as:

3

\frac{d w}{d x} = - θ_{x} + \frac{h^{2}}{3.5} [\frac{\partial^{2} θ_{x}}{\partial x^{2}} + ν \frac{\partial^{2} θ_{y}}{\partial y \partial x}] + \frac{h^{2}}{10} [\frac{\partial^{2} θ_{x}}{\partial y^{2}} + \frac{\partial^{2} θ_{y}}{\partial y \partial x}],

4

\frac{d w}{d y} = - θ_{y} + \frac{h^{2}}{3.5} [\frac{\partial^{2} θ_{y}}{\partial y^{2}} + ν \frac{\partial^{2} θ_{x}}{\partial y \partial x}] + \frac{h^{2}}{10} [\frac{\partial^{2} θ_{y}}{\partial x^{2}} + \frac{\partial^{2} θ_{x}}{\partial y \partial x}],

substituting Eq. (1) and Eq. (2) in Eq. (3) and Eq. (4) we get:

5

\frac{d w}{d x} = - α p c o s p x s i n q y [1 + \frac{h^{2}}{3.5} (p^{2} + v q^{2}) + \frac{h^{2}}{5} (q^{2})],

6

\frac{d w}{d y} = - α q s i n p x c o s q y [1 + \frac{h^{2}}{3.5} (q^{2} + v p^{2}) + \frac{h^{2}}{5} (p^{2})] .

Integrating above equations and after evaluating the constant of integration as:

7

w_{x} = - α s i n p x s i n q y [1 + \frac{h^{2}}{3.5} (p^{2} + v q^{2}) + \frac{h^{2}}{5} (q^{2})],

8

w_{y} = - α s i n p x s i n q y [1 + \frac{h^{2}}{3.5} (q^{2} + v p^{2}) + \frac{h^{2}}{5} (p^{2})],

where $p = π / a$ and $q = π / b$ . The expression for strain energy of moderately thick rectangular plate is given as:

9

U = \frac{D}{2} \int_{0}^{b} \int_{0}^{a} ‍ \{{(\frac{\partial θ_{x}}{\partial x})}^{2} + {(\frac{\partial θ_{y}}{\partial y})}^{2} + 2 ν \frac{\partial θ_{x}}{\partial x} \frac{\partial θ_{y}}{\partial y} + 2 (1 - ν) \frac{\partial θ_{x}}{\partial y} \frac{\partial θ_{y}}{\partial x}\} d x d y

+ \frac{k G h}{2} \int_{0}^{b} \int_{0}^{a} ‍ \{{(\frac{d w}{d x} + θ_{x})}^{2} + {(\frac{d w}{d y} + θ_{y})}^{2}\} d x d y .

Substituting Eq. (1, 2), Eq. (5, 6) in Eq. (9) and after simplification we get strain energy as:

10

U = \frac{D}{2} α^{2} a b \{{(p^{2} + q^{2})}^{2} + (\frac{k 6 (1 - v)}{h^{2}} (p^{2} {(A - 1)}^{2} + q^{2} {(B - 1)}^{2}))\},

where:

A = [1 + \frac{h^{2}}{3.5} (p^{2} + v q^{2}) + \frac{h^{2}}{5} (q^{2})], B = [1 + \frac{h^{2}}{3.5} (q^{2} + v p^{2}) + \frac{h^{2}}{5} (p^{2})] .

The expression for kinetic energy of moderately thick rectangular plate plate is given as:

11

T = \frac{ρ h w_{L}^{2}}{2} \int_{0}^{b} \int_{0}^{a} [w^{2} + \frac{h^{2}}{12} (θ_{x}^{2} + θ_{y}^{2})] d x d y .

Substituting Eq. (1, 2) and Eq. (7) in Eq. (11) and after simplification we get:

12

T = \frac{ρ h ω_{L}^{2}}{2} α^{2} \frac{a b}{4} (A^{2} + \frac{h^{2}}{12} (p^{2} + q^{2})) .

By minimizing the Lagranzian with respect to undetermined coefficient $α$ we get the fundamental frequency parameter $λ$ :

13

\frac{\partial (U - T)}{\partial α} = 0 .

3. Large amplitude vibrations

The principle of conservation of total energy states that at any instant of time total energy is constant for any vibrating structure neglecting damping.

From the derived transverse displacement field $w$ for an assumed $θ_{x}$ and $θ_{y}$ the strain energy and the kinetic energy in the plate are derived and is discussed in the previous section. In order to evaluate the large amplitude free vibrations of the plate the work done due to the stretching of the central plane of the plate has to be derived. The expression for tension developed in the plate due to large amplitudes in $x$ direction is given as:

14

T_{x} = \frac{E h}{2 a} {\int_{0}^{a} \{\frac{d w (x)}{d x}\}}^{2} d x,

15

T_{x} = \frac{E h}{4} α^{2} \frac{π^{2}}{a^{2}} .

Shear flexible terms are not involved in the expression of tension because the tension in the plate is only caused by stretching of the mid plane due to bending and not due to shear. Similarly, the tension in y direction is given as:

16

T_{y} = \frac{E h}{2 b} \int_{0}^{b} {\{\frac{d w (y)}{d y}\}}^{2} d y,

17

T_{y} = \frac{E h}{4} α^{2} \frac{π^{2}}{b^{2}} .

The expression for work done is given as:

18

W = \frac{1}{2} \int_{0}^{b} \int_{0}^{a} \{\frac{1}{2} T_{x} {(\frac{d w}{d x})}^{2} + \frac{1}{2} T_{y} {(\frac{d w}{d y})}^{2}\} d x d y .

Substituting Eq. (5-6), Eq. (17) and Eq. (19) in Eq. (18) and after simplification we get:

19

W = α^{4} \frac{E h}{64} a^{2} x (p^{4} A^{2} + q^{4} B^{2}) .

By principle of conservation of total energy:

20

U + T + W = c o n s t a n t .

Substituting Eq. (10), Eq. (12) and Eq. (19) in Eq. (20) and after simplification:

21

{\dot{z}}^{2} + α_{1} z^{2} + α_{2} z^{4} = c o n s t a n t .

Substituting $D = E h^{3} / 12 (1 - ν^{2})$ , $b = a x$ and after simplification

22

λ = α_{1} = \frac{ρ h ω_{L}^{2} a^{4}}{D} = \frac{π^{4} [{(1 + {(\frac{1}{x})}^{2})}^{2} + k 6 (1 - v) π^{2} (A_{1}^{2} + {(\frac{B_{1}}{x})}^{2}) {(\frac{h}{a})}^{2}]}{[{(1 + π^{2} A_{1} {(\frac{h}{a})}^{2})}^{2} + \frac{π^{2}}{12} (1 + {(\frac{1}{x})}^{2}) {(\frac{h}{a})}^{2}]},

23

α_{2} = \frac{ρ h ω_{N L}^{2} a^{4}}{D} = \frac{π^{4} \frac{3}{2} (1 - v^{2}) [{(1 + A_{1} π^{2} {(\frac{h}{a})}^{2})}^{2} + \frac{1}{x^{4}} {(1 + B_{1} \frac{π^{2}}{x^{2}} {(\frac{h}{a})}^{2})}^{2}]}{[{(1 + π^{2} A_{1} {(\frac{h}{a})}^{2})}^{2} + \frac{π^{2}}{12} (1 + {(\frac{1}{x})}^{2}) {(\frac{h}{a})}^{2}] {(\frac{α_{m}}{h})}^{- 2}},

where:

A_{1} = \frac{1}{3.5} (1 + v \frac{1}{x^{2}}) + \frac{1}{5 x^{2}}, B_{1} = \frac{1}{3.5} (\frac{1}{x^{2}} + v) + \frac{1}{5}, b = a x .

By applying harmonic balance method [2] and simplifying, the expression for frequency ratio can be written as:

24

{[\frac{ω_{N L}}{ω_{L}}]}^{2} = 1 + \frac{9}{4} (\frac{(1 - υ^{2}) [{(1 + A_{1} π^{2} {(\frac{h}{a})}^{2})}^{2} + \frac{1}{x^{4}} {(1 + B_{1} \frac{π^{2}}{x^{2}} {(\frac{h}{a})}^{2})}^{2}] {(\frac{α_{m}}{h})}^{2}}{[{(1 + {(\frac{1}{x})}^{2})}^{2} + k 6 (1 - v) π^{2} (A_{1}^{2} + {(\frac{B_{1}}{x})}^{2}) {(\frac{h}{a})}^{2}]}) .

The Eq. (24) gives the expression for frequency ratio in terms of plate thickness ratio $(h / a)$ and maximum amplitude ratio $(α_{m} / h)$ .

Table 1Values of linear fundamental frequency parameter (λ ) for all edges simply supported moderately thick rectangular plate at different aspect ratios.

Aspect ratio ( $b / a$ )
$\frac{h}{a}$	1		1.5		2		2.5
$\frac{h}{a}$	CDF	Ref	CDF	Ref	CDF	Ref	CDF	Ref
0.001	19.7391	19.7415* 19.7362a 19.7395d	14.2560	14.2561a 14.2566d	12.3370	12.3389* 12.3370d	11.4487	11.4487a 11.4507d
0.05	19.5152	19.2271* 19.5676c	14.1095	14.1662c	12.2224	12.1770* 12.2696c	11.3485	11.3906c
0.1	18.8877	18.3464* 19.0650b 19.0840c 19.0651d	13.6917	13.898b 13.9085c 13.8984d	11.8935	11.8515* 12.0675b 12.0752c 12.0676d	11.0598	11.2158b 11.226c 11.2158d
0.15	17.9679	17.3727* 18.3661c	13.0600	13.5147c	11.3900	11.4468* 11.7747c	10.6154	10.9617c
0.2	16.8857	16.3713* 17.4524b 17.5055c 17.3999d	12.2881	12.9933b 13.0250c 12.9923d	10.7647	10.9936* 11.3717b 11.3961c 11.3708d	10.0591	10.6088b 10.6307c 10.6078d
Values are taken from * [4], a [9], b [10], c [11], d [13]

4. Numerical results and discussion

Using the formulation described above, the large amplitude vibration behavior of a uniform moderately thick rectangular plates for different aspect ratios were obtained in terms of $ω_{N L} / ω_{L}$ or $T_{N L} / T_{L}$ (Ratio of non-linear radian frequency to the linear radian frequency or non-linear time period to the linear time period) in terms of various $α_{m} / h$ (maximum amplitude ratios) and h/a (plate thickness ratios). As a demonstration of the proposed formulation, the moderately thick rectangular plates are considered with axially immovable edges (Fig. 1).

The present results in terms of fundamental frequency parameter are presented in Table 1 for all edges simply supported moderately thick rectangular plate. For comparison and validation of the proposed method, similar results obtained by the finite element method [4] and other researchers are included in Table 1. From Table 1 it is found that for a particular given aspect ratio the fundamental frequency parameter decreases with increase of plate thickness ratio. For a given aspect ratio of 2.5, further reduction in frequency parameter is observed in case of moderately thick plates.

The present results in terms of $T_{N L} / T_{L}$ which is the reciprocal of $ω_{N L} / ω_{L}$ for all edges simply supported moderately thick rectangular plate are given in Table 2 to Table 5 respectively for different aspect ratios. The present results for the extreme case of $α_{m} / h =$ 1 and $h / a =$ 0.2 match very well with the results of FEM and other researchers. It is found from the Table 2 to Table 4 that the frequencies are increasing with increase of amplitude ratio. More nonlinearity is observed with the increase in aspect ratio in rectangular plates when compared to square plates.

Further, the present results match excellently with those of [13] for the thin plates, showing the efficacy of the proposed method and the accuracy of the results over a range of $h / a =$ 0.001 and $h / a =$ 0.2. Further, no shear locking phenomenon exists in the present formulation.

Table 2TNL/TL values of all edges simply supported moderately thick square plate (b/a= 1)

$\frac{h}{a}$	$α_{m} / h$
	0		0.2		0.4		0.6		0.8		1.0
	CDF	FEM [4]	CDF	FEM [4]	CDF	FEM [4]	CDF	FEM [4]	CDF	FEM [4]	CDF	FEM [4]
0.001	1	1	0.9801	0.9818 0.9821* 0.9809$ 0.9783#	0.9269	0.9327 0.9338* 0.9297$ 0.9210#	0.8548	0.8652 0.8673* 0.8602$ 0.8451#	0.7773	0.7916 0.7943* 0.7853$ 0.7653#	0.7029	0.7199 0.7233* 0.7131$ 0.6901#
0.05	1	1	0.9798	0.9807	0.9257	0.9290	0.8526	0.8586	0.7744	0.7827	0.6996	0.7098
0.1	1	1	0.9787	0.9788	0.9220	0.9226	0.8462	0.8475	0.7658	0.7681	0.6898	0.6931
0.15	1	1	0.9768	0.9766	0.9159	0.9153	0.8356	0.8350	0.7519	0.7520	0.6741	0.6752
0.2	1	1	0.9742	0.9740	0.9074	0.9069	0.8213	0.8212	0.7337	0.7347	0.6537	0.6562
Values are taken from * [7], $ [6], # [5]

Table 3TNL/TL values of all edges simply supported moderately thick plate (b/a= 1.5)

$\frac{h}{a}$	$α_{m} / h$
$\frac{h}{a}$	0	0.2	0.4	0.6	0.8	1
0.001	1	0.9773	0.9174	0.8383	0.7555	0.6780
0.05	1	0.9769	0.9163	0.8363	0.7529	0.6751
0.1	1	0.9759	0.9128	0.8303	0.7452	0.6665
0.15	1	0.9741	0.9069	0.8204	0.7326	0.6525
0.2	1	0.9715	0.8986	0.8067	0.7154	0.6337

Table 4TNL/TL values of all edges simply supported moderately thick rectangular plate (b/a= 2)

$\frac{h}{a}$	$α_{m} / h$
	0		0.2		0.4		0.6		0.8		1.0
	CDF	FEM [4]	CDF	FEM [4]	CDF	FEM [4]	CDF	FEM [4]	CDF	FEM [4]	CDF	FEM [4]
0.001	1	1	0.9733	0.9768	0.9043	0.9161	0.8162	0.8367	0.7272	0.7550	0.6465	0.6795
0.05	1	1	0.9729	0.9761	0.9031	0.914	0.8141	0.8332	0.7245	0.7506	0.6436	0.6747
0.1	1	1	0.9717	0.9749	0.8992	0.91	0.8076	0.8266	0.717	0.7423	0.6351	0.6658
0.15	1	1	0.9696	0.9733	0.8928	0.9049	0.7973	0.8186	0.7038	0.7325	0.6212	0.6554
0.2	1	1	0.9667	0.9714	0.8836	0.899	0.7829	0.8092	0.6864	0.7213	0.6025	0.6437

Table 5TNL/TL values of all edges simply supported moderately thick rectangular plate (b/a= 2.5)

$\frac{h}{a}$	$α_{m} / h$
$\frac{h}{a}$	0	0.2	0.4	0.6	0.8	1
0.001	1	0.9702	0.8945	0.8002	0.7073	0.6249
0.05	1	0.9697	0.8932	0.7980	0.7047	0.6221
0.1	1	0.9684	0.8892	0.7914	0.6968	0.6137
0.15	1	0.9663	0.8824	0.7809	0.6840	0.6001
0.2	1	0.9631	0.8728	0.7662	0.6666	0.5818

5. Conclusions

The complex structures in various fields of engineering such as Aerospace, Mechanical, Civil, Naval, Nuclear, and Automobile are made up of simple structural members like beams, plates (thin or moderately thick) and shells. Due to functional requirements sometimes these structural members may be either thin or moderately thick. If these structural members are subjected to severe dynamic environment, they vibrate with large amplitudes. The authors evaluated free vibration response i.e. natural frequencies both in the linear and nonlinear regime.

The concept of coupled displacement field method (CDF) is successfully applied to study the large amplitude free vibrations of all edges simply supported moderately thick rectangular plate for different aspect ratios. Elegant and closed form expressions are derived in terms of maximum amplitude ratio $(α_{m} / h)$ and plate thickness ratio $h / a$ using single term admissible functions for the total rotations $θ_{x}$ and $θ_{y}$ . The closed form expressions are obtained for non-dimensional frequency parameter as a function of thickness ratio $h / a$ and frequency ratio or the time period ratio as a function of maximum amplitude ratio $α_{m} / h$ and plate thickness ratio $h / a$ . Comparison of present results wherever possible for the first mode of vibration with the available open literature shows that the coupled displacement field method gives accurate values for the linear frequency parameter and ratios of nonlinear to linear frequencies.

The natural frequencies are useful for the design engineers for the purpose of design of various structural members. Using the results given in Tables 1-6 failure of the structural member can be predicted based on the stiffness approach.

References

Zhou D. Free vibration of multi-span Timoshenko beams using static Timoshenko beam functions. Journal of Sound and Vibration, Vol. 241, 2001, p. 725-734.

Publisher
Rao G. V., MeeraSaheb K., Rangajanardhana G. Concept of coupled displacement field for large amplitude free vibrations of shear flexible beams. American Society of Mechanical Engineering, Vol. 128, 2006, p. 251-255.

Publisher
Mindlin R. D. Influence of rotary inertia and shear on flexural motions of isotropic elastic plates. Journal of Applied Mechanics, Vol. 18, 1951, p. 31-38.

Publisher
Raju K. K., Rao G. V., Raju I. S. Effect of geometric nonlinearity on large amplitude free flexural vibrations of moderately thick rectangular plates. Computers and Structures, Vol. 9, 1978, p. 441-444.

Publisher
Wah T. Large amplitude flexural vibration of rectangular plates. International Journal of Mechanical Sciences, Vol. 5, 1963, p. 425-438.

Publisher
Chu H. N., Herrman G. Influence of large amplitudes on free flexural vibrations of rectangular elastic plates. Journal of Applied Mechanics, Vol. 23, 1956, p. 532-540.

Publisher
Chu Mei Finite element displacement method for large amplitude free flexural vibrations of beams and plates. Computers and Structures, Vol. 3, 1973, p. 163-174.

Publisher
Wang C. M., Wang C. Y., Reddy J. N. Exact Solutions for Buckling of Structural Members. CRC Press, 2005.

Publisher
Leissa W. The free vibration of rectangular plates. Journal of Sound and Vibration, Vol. 31, Issue 3, 1973, p. 257-293.

Publisher
Milan Batista Analytical solution for free vibrations of simply supported transversally inextensible homogeneous rectangular plate. arXiv:1007.2539, 2010.

Search CrossRef
Hashemi H. S., Arsanjani M. Exact characteristic equations for some of classical boundary conditions of vibrating moderately thick rectangular plates. International Journal of Solids and Structures, Vol. 42, 2005, p. 819-853.

Publisher
Liew K. M., Xiang Y., Kitipornchai S. Transverse vibration of thick rectangular plates. Part 1: Comprehensive sets of boundary conditions. Computers and Structures, Vol. 49, 1993, p. 1-29.

Publisher
Raju K. K., Hinton E. Natural frequencies and modes of rhombic Mindlin plates. Earthquake Engineering Structural Dynamics, Vol. 8, 1980, p. 55-62.

Publisher
Gorman D. J. Free Vibration Analysis of Rectangular Plates. Elsevier North Holland, New York.

Search CrossRef

Cited by

Large amplitude forced vibrations of Timoshenko beams using coupled displacement field method

K. Meera Saheb | Gopichand Kanneti | Prabhakar Sathujoda

(2022)

About this article

Received

01 February 2016

Accepted

28 June 2016

Published

30 September 2016

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/jve.2016.16889

Keywords

coupled displacement field method

large amplitude vibrations

moderately thick rectangular plates

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 03 02

An analytical model for the analysis of vibration and energy flow in a clamped stiffened plate using integral transform technique

Hui Guo, Kai Zhang

Research article

2021 01 08

Minimizing the radiated sound power from vibrating plates by using in-plane functionally graded materials

Nabeel Alshabatat, Koorosh Naghshineh

Research article

2019 11 28

Free vibration analysis of simply supported rectangular plates

Ganesh Naik Guguloth, Baij Nath Singh, Vinayak Ranjan

Research article

2017 09 30

Shooting method for free vibration of FGM Reissner-Mindlin circular plates resting on elastic foundation in thermal environments

Qing-Lu Li, Wei-Di Luan, Zuo-Quan Zhu

K. Bhaskar K and M. Saheb K, “Large amplitude free vibrations of simply supported moderately thick rectangular plates using coupled displacement field method,” Journal of Vibroengineering, Vol. 18, No. 6, pp. 3451–3458, Sep. 2016, https://doi.org/10.21595/jve.2016.16889

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2016.16889
UR  - https://doi.org/10.21595/jve.2016.16889
TI  - Large amplitude free vibrations of simply supported moderately thick rectangular plates using coupled displacement field method
T2  - Journal of Vibroengineering
AU  - Bhaskar K, Krishna
AU  - Saheb K, Meera
PY  - 2016
DA  - 2016/09/30
PB  - JVE International Ltd.
SP  - 3451-3458
IS  - 6
VL  - 18
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Bhaskar_K_2016,
	doi = {10.21595/jve.2016.16889},
	url = {https://doi.org/10.21595/jve.2016.16889},
	year = 2016,
	month = {sep},
	publisher = {{JVE} International Ltd.},
	volume = {18},
	number = {6},
	pages = {3451--3458},
	author = {Krishna Bhaskar K and Meera Saheb K},
	title = {Large amplitude free vibrations of simply supported moderately thick rectangular plates using coupled displacement field method},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]K. Bhaskar K and M. Saheb K, “Large amplitude free vibrations of simply supported moderately thick rectangular plates using coupled displacement field method,” Journal of Vibroengineering, vol. 18, no. 6, pp. 3451–3458, Sep. 2016, doi: 10.21595/jve.2016.16889.

Copy IEEE

Copied to clipboard!

Bhaskar K, Krishna, and Meera Saheb K. “Large Amplitude Free Vibrations of Simply Supported Moderately Thick Rectangular Plates Using Coupled Displacement Field Method.” Journal of Vibroengineering 18, no. 6 (September 30, 2016): 3451–58. https://doi.org/10.21595/jve.2016.16889.

Copy Chicago

Copied to clipboard!

Large amplitude free vibrations of simply supported moderately thick rectangular plates using coupled displacement field method

Abstract

1. Introduction

2. Coupled displacement field (CDF) method for plates

3. Large amplitude vibrations

4. Numerical results and discussion

5. Conclusions

References

Cited by

About this article

Related Articles