Vibration performance analysis of vehicle with the non-pneumatic new mechanical elastic wheel in the impulse input experiment

Wei, Wang; Kai, Zhu; Shaoyi, Bei; Lanchun, Zhang; Yongzhi, Wang

doi:10.21595/jve.2016.16988

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 September 2016

Check for updates

Vibration performance analysis of vehicle with the non-pneumatic new mechanical elastic wheel in the impulse input experiment

Wang Wei¹

Zhu Kai²

Bei Shaoyi³

Zhang Lanchun⁴

Wang Yongzhi⁵

^{1, 2, 3, 4, 5}School of Automotive and Traffic Engineering, Jiangsu University of Technology, Jiangsu, Changzhou, 213001, China

Corresponding Author:

Zhu Kai

Cite the article Download PDF

Downloads 1975

WoS Core Citations 4

CrossRef Citations 4

Abstract

A non-pneumatic tire appears to have advantages over the conventional pneumatic tire in terms of flat proof and maintenance free. A mechanical elastic wheel (MEW) with a non-pneumatic elastic outer ring which functions as the air of the pneumatic tire was presented. The structure of MEW is non-inflatable integrated configuration and the effect of hinges is accounted for only in tension. To establish finite element model of MEW, various nonlinear factors, such as the geometrical nonlinearity, material nonlinearity and contact nonlinearity, were considered. Load characteristic test was conducted by tyre dynamic test-bed to obtain force-deflection curves. And the validity of the finite element model was validated through load characteristic test. The vehicle vibration performance respectively based on the MEW and the radial tire was compatative studied under pulse input experiment conditions. The result showed that the vehicle concluding the new mechanical elastic wheel met the vibration performance requirements and vibration performance regularity of pneumatic tire. The results could be used as the thesis reference for the improvement of new mechanical elastic wheel.

1. Introduction

Since the first commercial pneumatic bicycle tire by Dunlop in 1888, the pneumatic tire has been dominant in the world tire market for more than 100 years due to four major advantages it has over a rigid wheel: (i) low energy loss on rough surfaces, (ii) low vertical stiffness, (iii) low contact pressure, and (iv) low mass. However, the pneumatic tire has several disadvantages as well: (i) the possibility of catastrophic damage – a flat while driving, (ii) the required maintenance for proper internal air pressure, and (iii) the complicated manufacturing procedure [1].

Wheel and tire are as important components of vehicle driving system, which play an important role in riding comfort, and its main functions are to support vehicles, ease road impact, and generate driving or braking force. However, pneumatic tire burst at high speed may cause fatal traffic accident. According to statistics, 46 % of highway accidents were caused by tire failures, where tire burst accounted for 70 % of total accidents, and mortality rate caused by tire burst at a speed of more than 160 km was close to 100 % [2]. Therefore, developing run-flat and anti-puncture tire to guarantee high performance and security has become a consensus of the world’s major tire manufacturers.

To reduce the pneumatic tire disadvantages, several tire engineers have attempted to develop non-pneumatic tires, such as Uniroyal Goodrich Tire, Bridgestone, Toyo Tire and Tweel [3-8]. In this study, a mechanical elastic wheel (MEW) for a off-road vehicle which is a special kind of the non-pneumatic tire is proposed. Systematic research on its modeling, mechanical properties and trafficability indicate that the proposed wheel has small rolling resistance, good trafficability and other good characteristics [9-11]. The vehicle vibration performance respectively based on the MEW and the radial tire is comparative studied under pulse input experiment conditions. The research results provide references for optimization of wheel structure and vehicle dynamic.

2. MEW structure analysis

MEW breaks split design between traditional wheel and pneumatic tire, and adopts non-pneumatic structure which uses hinges group to connect elastic outer wheel and rigid wheel hub, so tire burst and puncture does not exist. The wheel consists of an elastic outer wheels, hinges group, wheel hub, return spring and other components, as shown in Fig. 1. Furthermore, elastic outer wheel consists of elastic rings, elastic ring clamps and rubber layer with tread patterns.

Fig. 1Structure of MEW

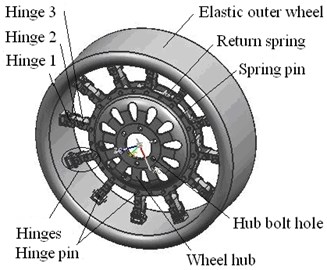
a) General assembly drawing of MEW

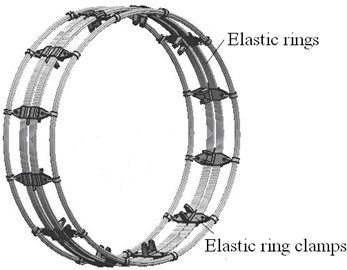
b) Structure of elastic ring mechanism

2.1. The structure of new mechanical elastic wheel

MEW is composed of the driving apron, elastic rings, the combo cards of elastic rings, hub, return spring, pins, hinges and other accessories. Its structure is shown in Fig. 1.

(1) 12 combo cards of elastic rings are distributed with the same angle and combined and locked a plurality of elastic rings together, as shown in Fig. 1(b).

(2) By burying vulcanization in the rubber layer of driving apron and inner layer of cord fabric, the elastic outer-wheel is built.

(3) The hub is put in the middle of the elastic outer wheel. One end of 12 groups of hinges is respectively installed with pins on the pin seat of the combo cards of elastic rings of the elastic outer wheel inner side. The other end of them is installed on the bolt hole of wheel hub.

(4) A return spring at the bottom of the third hinge connected to the hub. In free state, the groups of hinges are slightly bending deflection. Because of ground shocking and the driving and braking torque, the hinges are curved in the vehicle driving process. The curved hinges can be returned through the return spring.

2.2. The working principle of new mechanical elastic wheel

(1) The load and torque by axle passed the hub make the groups of hinges from flexuosity to pretension state. Then, the hinges pull the elastic outer-wheel. The force is making the wheel roll.

(2) The hub relying on the pull from the hinges hang into the outer-wheel and move down a distance due to vertical load. The hinges under the hub don’t subjected to force and are slightly curved. The upper part of elastic outer-wheel due to the downward pull from the hub, outer-wheel transform into the appropriate class of elliptic elastic deformation with setting range.

(3) Because of outer-wheel transforming into elliptic, the deformation of MEW is different from local deformation of the pneumatic tire under the driving process. It shows the rolling resistance and energy consumption of MEW is much smaller than that of the pneumatic tire and mechanical efficiency is much higher than that of the pneumatic tire.

(4) The MEW under the loading driving process, the force of each groups of hinges is from the tension gradually to the slightly bent not force, then to the tension, cycle replacement cycle. Because of the hub is put in the middle of the elastic outer wheel, the most of incentive of road roughness can only be suffered by the elastic outer-wheel. Because of deformation of the outer-wheel and the instantaneous curvature of each groups of hinges, incentive of road roughness cannot be sent to the wheel hub. The MEW has a specific mitigation and buffering isolation performance different from the pneumatic tire.

3. Finite element modeling of MEW

3.1. Establishment of Finite Element Model

Wheel outer elastic rims are simplified as four groups of elastic rigid rims which are fixed together by elastic rim clamps, and sharp corners of the structure, tire crown patterns and other factors are ignored. Simplified outer rim model of elastic wheel includes tire crown, belt, elastic rigid rim and tire carcass, as shown in Fig. 2(a). Fig. 2(b) is the finite element mesh model.

Fig. 23D FE model of an elastic wheel

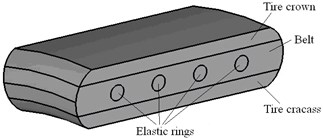
a) Structure of elastic outer wheel

b) 3D mesh model of MEW

The mechanical elastic wheel model was meshed by HyperMesh, and due to the complex structure, mixed elements were used, where hexahedral element was in the majority, pentahedron element was in the minority. In order to guarantee certain grid density, the size of the element was based on to the structure. The main control parameters of element quality were as follows: the maximum length-width ratio was 3, the minimum Jacobi was 0.8, the maximum surface distortion was 35°, the minimum quadrilateral interior angle was 50°, the maximum quadrilateral interior angle was 130°, the minimum triangle interior angle was 45°, and the maximum triangle interior angle was 75°. The model was divided into 307632 body elements, with a total of 374774 nodes, and minimum element size was controlled in 2 mm. After meshing, element continuity and grid quality of repetitive elements were check, to ensure the grid deformation was in a certain range. Deformation of MEW under vertical load is shown in Fig. 3.

Fig. 3Deformation of MEW finite element model

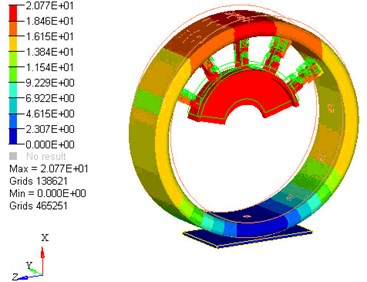
The main contacts in the wheel model were: elastic ring and outer wheel, elastic ring and hinge, internal hinge, hinge group and wheel hub. The main contacts above were defined according to the characters of wheel structure and movement relationships between each component. The element rbe2 was used between elastic ring and outer wheel, and the rest of the contacts were revolute pair with mutual movement. Therefore, the contacts with the other three parts were defined as sliding contact, and sliding friction coefficient was 0.15.

3.2. Nonlinear characteristic of MEW

Outer rim of elastic wheel has a hierarchical structure, so nonlinear factors of materials and boundary conditions need to be considered in modeling, in addition, large deformation and nonlinear effects of contact with ground should be considered because wheel deformation is mainly undertaken by elastic outer rim. Rubber entity unit of mechanical elastic wheel uses approximate incompressible super elastic rubber material model; which incompressibility condition is represented by Poisson ratio $v =$ 0.48.

Tire tread model uses Mooney-Rivlin material according to characteristics of this study. The structural relationship of rubber materials is complex nonlinear functions, which can be expressed by Mooney-Rivlin strain energy density function, and its expression is:

1

W = \sum_{i + j = 1}^{N} C_{i j} {(I_{1} - 3)}^{I} {(I_{2} - 3)}^{j} + \sum_{k = 1}^{N} \frac{1}{d_{k}} {(I_{3}^{2} - 1)}^{2 k},

where, $N$ , $C_{i j}$ , $d_{k}$ are material constants.

The typical two third-order expansion of Mooney-Rivlin strain energy density function is widely used, and when the strain is within 150 %, most rubber materials can receive reasonable approximation, as shown in Eq. (2):

2

W = C_{10} (I_{1} - 3) + C_{01} (I_{2} - 3) + \frac{1}{d} {(I_{3} - 1)}^{2},

where, $I_{1}$ , $I_{2}$ , $I_{3}$ are strain invariants represented by primary elongations, and for incompressible material, $I_{3} =$ 1.

Furthermore, considering viscoelasticity characteristics of rubber materials, Prony series model is generally used to express its viscoelasticity, and its expression is:

3

\{\begin{array}{l} g_{R} (t) = 1 - \sum_{i = 1}^{N} {\bar{g}}_{i}^{p} (1 - e^{- t / τ_{_{i}}}), \\ k_{R} (t) = 1 - \sum_{i = 1}^{N} {\bar{k}}_{i}^{p} (1 - e^{- t / τ_{i}}), \end{array}

where, $g_{R} (t)$ is shear relaxation modulus, $k_{R} (t)$ is volume relaxation modulus, ${\bar{g}}_{i}^{p} (t)$ is shear relaxation modulus factor of the series $i$ , ${\bar{k}}_{i}^{p} (t)$ is volume relaxation modulus factor of the series $i$ , and $τ_{i}$ is relaxation time.

The wheel has typical large deformation characteristics when working, so it is limited that using traditional linearelastic small strain theory to study structural mechanics. Therefore, geometric nonlinearity large deformation theory must be considered. Total Lagrange is used to solve geometric nonlinearity, and the relationship between Green strain and Kirchhoff stress based on the principle of virtual work is:

4

\int_{0}^{t + Δ t} {}_{0} S_{i j} S^{t + Δ t} {}_{0} E_{i j} d V = δ^{t + Δ t} ω .

Then use variation method:

5

\int_{0}^{t + Δ t} ({}_{0} S_{i j} + Δ_{0} S_{i j}) δ ({}_{0} E_{i j} + Δ_{0} E_{i j}) d ω = δ^{t + Δ t} ω .

Finite element equation matrix with geometric nonlinearity TL method can be expressed as:

6

({[K]}_{0} + {[K]}_{σ} + {[K]}_{L}) \{δ q\} = \{F\} + \{T\} + \{P\},

where, ${[K]}_{0}$ is tangent stiffness matrix, presenting the relationship between load increment and displacement, ${[K]}_{σ}$ is initial

stress stiffness matrix or geometric stiffness matrix, presenting the effect of initial stress on the structure in large deformationcases, ${[K]}_{L}$ is initial displacement stiffness matrix or large displacement stiffness matrix, presenting structure stiffness changes along with large displacement, $\{δ q\}$ is node coordinates increment vector, $\{F\}$ is body load vector, $\{T\}$ is surface load vector, and $\{P\}$ is stress equivalent resultant force vector on the node.

There are two contacts, elastic rigid rim and rubber material, tire tread and ground, in mechanical elastic wheel finite element model, and them belong to functional extreme value problem with constraints, so penalty function method is used to predict normal force, and Coulomb friction model should be used to predict tangential force.

Normal force is:

7

f_{n} = \{\begin{array}{l} K_{n} C, C \leq 0, \\ 0, C > 0, \end{array}

where, $K_{n}$ is normal contact stiffness, and $C$ is gap value determined by contact node position relative to target surface.

Tangential force is:

8

f_{s} = \{\begin{array}{l} K_{t} η, adhesive contact, \\ μ f_{n}, sliding contact, \end{array}

where, $K_{t}$ is shear stiffness, $η$ is elastic deformation of contact node relative to target surface, and $μ$ is sliding coefficient of friction.

Fig. 4Load-deflection curve of MEW

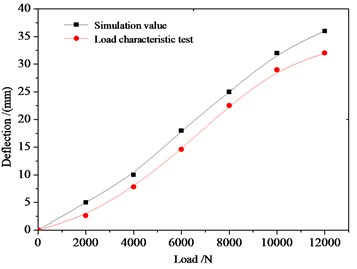
Fig. 5A vehicle equipped with MEW

3.3. Validation of Finite Element Model

To verify the model, load characteristic test was conducted, and compared the results with prototype load characteristic curve, as shown in Fig. 4. The load characteristic test is shown in Fig. 5.

The figure shows that load characteristic curve of mechanical elastic wheel is nearly linear, simulation results are consistent with experimental results, which verifies that the finite element model can accurately reflect actual bearing of elastic wheel. All these researches establish foundation for vibration characteristic analysis of the wheel at still state.

4. Vibration performance analysis of Vehicle in the impulse input experiment

4.1. Experiment method

According to national standard GB/T4970-2009: the triangle single bump method is used in pulse input experiment shown as in Fig. 6. The hemline length and the height of triangle bump are respectively 400 mm and 80 mm. The off-road vehicle drives through bump at the speed of 20, 40, 60, 80, 100 km/h. The maximum vertical acceleration is used to evaluate vehicle.

Fig. 6Triangle bump

4.2. Comparative analysis of the experiment results

In the experiment, the test point is set on the vehicle’s mass center. The vertical acceleration curve at different speed is shown as in Fig. 7. When the off-road vehicle drives through bump, it endure the big shock. Whether the vehicle is based on the mechanical elastic wheel or the radial tire, the acceleration variation trend is similar at different speeds.

When the speed is lower than 60 km/h, the acceleration peak value increases with vehicle’s speed.

Table 1 is the vertical acceleration values of off-road vehicle based on the MEW at different speeds and Table 2 is the vertical acceleration values of off-road vehicle based on the radial tire at different speeds. The vertical acceleration peak values of off-road vehicle based on MEW increase firstly and then decrease with the increasing speed. The vertical acceleration peak values of off-road vehicle based on the radial tire increase firstly and then remain unchanged with the increasing speed. The peak vertical acceleration of both tires at different speeds are similar.

Table 1The vertical acceleration values of off-road vehicle based on the MEW at different speeds

Speed(km/h)	20	40	60	80	100
vertical acceleration(m/s^2)	10.7	11.1	11.1	11.0	10.8

Table 2The vertical acceleration values of off-road vehicle based on the radial tire at different speeds

Speed(km/h)	20	40	60	80	100
vertical acceleration(m/s^2)	12.6	13.5	13.7	13.7	13.7

Referring to the international criteria ISO2631-1 of health assessment method for systemic exposure vibration, if the maximum acceleration response transferred to passenger by the surface of the seat cushion is greater the 43.02 m/s², it will do harm to the human body. If it is smaller than the 31.44 m/s², there is nothing to do with the human body health. And if the acceleration response lies in the range of 31.44-43.02 m/s², a certain extent of harm will put on human body. As can be seen from the Table 1 and Table 2, whether the vehicle is based on the mechanical elastic wheel or the radial tire, the maximum acceleration response values are less than 31.44 m/s². The off-road vehicle respectively based on the MEW and the radial tire meet the vibration performance requirements in the impulse input experiment.

Fig. 7The vertical acceleration curve at different speed

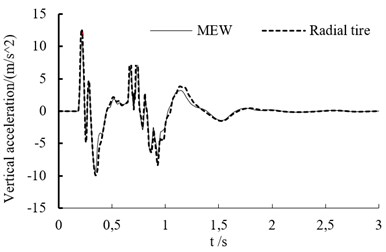
a) Vertical acceleration of vehicle mass center at the speed of 20 km/h

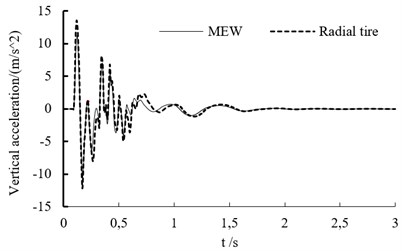
b) Vertical acceleration of vehicle mass center at the speed of 40 km/h

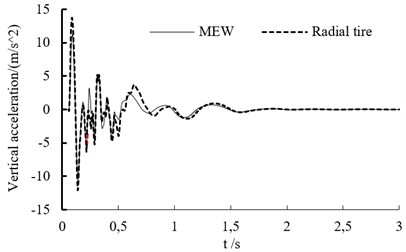
c) Vertical acceleration of vehicle mass center at the speed of 60 km/h

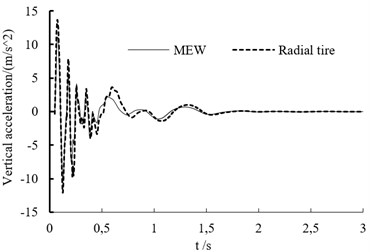
d) Vertical acceleration of vehicle mass center at the speed of 80 km/h

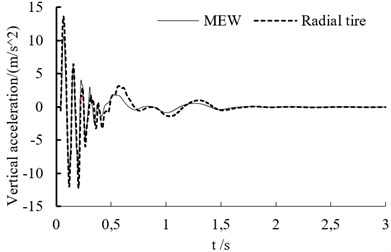
e) Vertical acceleration of vehicle mass center at the speed of 100 km/h

5. Vehicle ride quality simulation comparison

In this paper, the mechanical elastic wheel model and the vehicle model are built in the using ADAMS. In this paper vehicle model, ride comfort of vehicle between mechanical elastic wheel and the radial tire are comparative analyze. The vehicle is set in the B road at 60 Km/h speed. Comparing the results of ride quality based on the mechanical elastic wheel vehicle centroid and the general radial tire vehicle centroid, we can get the acceleration curves of the $X$ axis (vertical), $Y$ axis direction (lateral) and $Z$ axis direction (radial) shown in Figs. 8 and 9.

Fig. 8The acceleration curves of the X axis, Y axis and Z axis on MEW

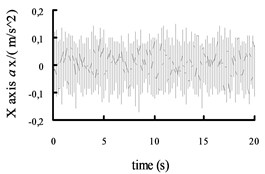
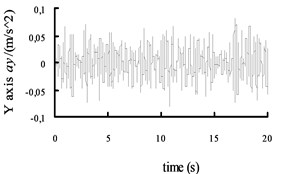
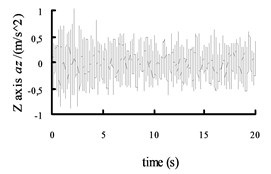
Fig. 9The acceleration curves of the X axis, Y axis and Z axis on the radial tire

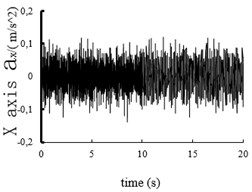
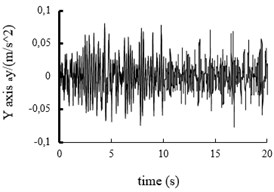
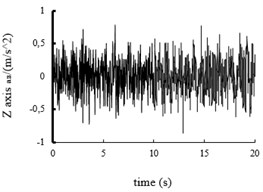
Fig. 10The acceleration power spectral density curves of the X axis, Y axis and Z axis on MEW

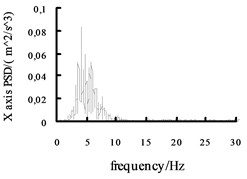
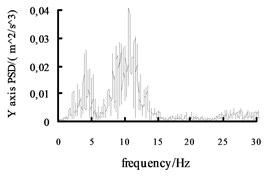
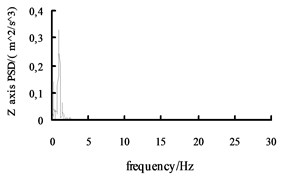
Fig. 11The acceleration power spectral density curves of the X axis, Y axis and Z axis on the radial tire

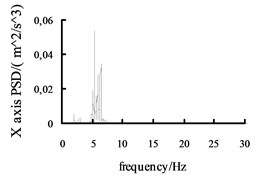
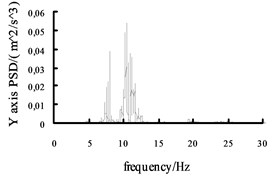
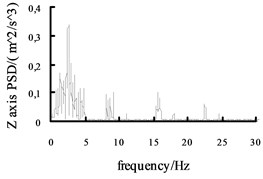
Using the Fast Fourier Transform (FFT) function of ADAMS post-processing to put the each direction acceleration curves into the acceleration power spectral density curves, and then the curves are obtained, shown in Fig. 10 and Fig. 11. It can be seen from the figure: the level $X$ , $Y$ direction acceleration power spectral density peak value of the vehicle based on the mechanical elastic wheel appear near the 4.2 Hz and 10.7 Hz position, avoiding 0.5-2 Hz sensitive range; while, the $X$ , $Y$ direction acceleration power spectral density peak of the vehicle based on the radial tire appears near the 5.6 Hz and 11.5 Hz position, also avoiding 0.5-2 Hz sensitive range. From Fig. 10 and Fig. 11, we can see the vertical $Z$ acceleration power spectral density peak of the vehicle based on the mechanical elastic wheel appears near the 1.1 Hz position, avoiding 4-12.5 Hz sensitive range. While, the vertical $Z$ acceleration power spectral density peak of the vehicle based on the pneumatic tire near the 2.5 Hz position, also avoiding the sensitive range of 4-12.5 Hz.

From the analysis above, mechanical elastic wheel can replace the role of the radial tire in Ride Comfort. According to the ISO 2631-1:1997 (E) standard, each axial frequency weighting function $W (f)$ is get from the Eq. (9). Each axial weighted acceleration mean square value $a_{x w}$ , $a_{y w}$ , $a_{z w}$ are obtained according to the formula 10 and 11 in the ADAMS post-processing:

9

W_{k} (f) = \{\begin{array}{l} 0.5, (0.5 \leq f < 2), \\ \frac{f}{4}, (2 \leq f < 4), \\ 1, (4 \leq f < 12.5), \\ \frac{1.25}{f}, (12.5 \leq f < 80), \end{array}

10

a_{w} = {[\int_{0.5}^{80} W^{2} (f) G_{a} (f) d f]}^{\frac{1}{2}},

11

a_{v} = [(1.4 a_{x w})^{2} + (1.4 a_{y w})^{2} + {a_{z w}}^{2}]^{\frac{1}{2}} .

In the same method, each axial weighted acceleration root-mean-square value and the total weighted root-mean-square acceleration are obtained at 40, 50, 70 km/h speed, the results are showed in Table 3 and Table 4.

The results can be obtained from the two tables:

1) As the speed increasing, the weighted acceleration root-mean-square value becomes large. It means that the ride comfort of the vehicle decreased with speed increasing. The ride comfort of the vehicle based on the radial tire at the different speed is slightly better than that of the mechanical elastic wheel, but the ride Comfort of the vehicle based on the mechanical elastic wheel satisfy with the regularity of the ride comfort of the vehicle based on the radial tire and conform with the characteristics of the radial tire.

2) According to the weighted acceleration root-mean-square value and human subjective feeling: when weighted acceleration $a_{w}$ is less than 0.315 m/s², the body is not uncomfortable. No matter based on the mechanical elastic wheel or the radial tire, the body is not uncomfortable when the vehicle speed is less than 60 km/h in B road. The mechanical elastic wheel is committed to improve the controllability and stability of vehicle. So when the vehicle with mechanical elastic wheel drive at the speed of 70 km/h, driver’s seat vibration response exceeds slightly the limit and the body has some uncomfortable. When the vehicle with the radial tire drive at the speed of 70 km/h, driver’s seat vibration response does not exceed the limit, the human feel comfortable. So, the ride comfort of mechanical elastic wheel under the condition of high speed needs to be improved.

Table 3Each axial weighted acceleration root-mean-square value on MEW

Speed (km/h)	$a_{x w}$ (m/s²)	$a_{x w}$ (m/s²)	$a_{x w}$ (m/s²)	$a_{x w}$ (m/s²)	Human subjective feeling
40	0.0799	0.0468	0.2237	0.2585	Comfortable
50	0.0869	0.0539	0.2454	0.2841	Comfortable
60	0.1015	0.0715	0.2484	0.3032	Comfortable
70	0.1163	0.0762	0.2671	0.3305	Some uncomfortable

Table 4Each axial weighted acceleration root-mean-square value on the radial tire

Speed (km/h)	$a_{x w}$ (m/s²)	$a_{x w}$ (m/s²)	$a_{x w}$ (m/s²)	$a_{x w}$ (m/s²)	Human subjective feeling
40	0.0639	0.0388	0.1422	0.1766	Comfortable
50	0.0768	0.0443	0.1451	0.1909	Comfortable
60	0.0896	0.0507	0.1543	0.2111	Comfortable
70	0.0984	0.0649	0.2445	0.2950	Comfortable

6. Conclusions

In this study, a kind of new mechanical elastic wheel used for vehicle is put forward, to improve the tire performance of puncture-proof, explosion prevention, safety and bullet-proof. MEW integrated tire and wheel combination is one of non-pneumatic tire which has potential for improved handling, grip, low energy loss when impacting obstacles and reduced rolling resistance when compared to a pneumatic tire. The objective of this study is to analysis vehicle vibration performance analysis with the non-pneumatic new mechanical elastic wheel in the impulse input experiment.

1) A new mechanical elastic wheel is non-pneumatic structure, which uses hinge groups to connect outer rim of elastic wheel and wheel hub, so it provides a new research idea for solving tire burst and puncture problems of pneumatic tires.

2) The vehicle vibration performance respectively based on the MEW and the radial tire was comparative studied under pulse input experiment conditions. The off-road vehicle drives through bump at the speed of 20, 40, 60, 80, 100 km/h. The result showed that the vehicle concluding the new mechanical elastic wheel met the vibration performance requirements and vibration performance regularity of pneumatic tire. The results could be used as the thesis reference for the improvement of new mechanical elastic wheel.

References

Gent A. N., Walter J. D. The Pneumatic Tire. National Highway Traffic Safety Administration, Washington, D.C., 1985.

Search CrossRef
In G. J., Young H. S., Eui J. Y., et al. Pattern design of a non-pneumatic tyre for stiffness using topology optimization. Engineering Optimization, Vol. 42, Issue 2, 2011, p. 119-131.

Publisher
Rhyne T., Cron S. M. Development of a non-pneumatic wheel. Tire Science and Technology, Vol. 34, Issue 3, 2006, p. 150-169.

Publisher
Ju J., Ananthasayanam B., Summers J. D., et al. Design of cellular shear bands of a non-pneumatic tire-investigation of contact pressure. SAE International Journal of Passenger Cars-Mechanical Systems, Vol. 3, Issue 1, 2010, p. 598-606.

Publisher
Jang I. G., Sung Y. H., Yoo E. J., et al. Pattern design of a non-pneumatic tyre for stiffness using topology optimization. Engineering Optimization, Vol. 44, Issue 2, 2012, p. 119-131.

Search CrossRef
Ju J., Kim D. M. Flexible cellular solid spokes of a non-pneumatic tire. Composite Structures, Vol. 94, Issue 8, 2011, p. 2285-2295.

Publisher
Manga K. K. Computation Method for Solving Spoke Dynamics on High Speed Rolling Tweel™. Master’s Thesis, Clemson University, Clemson, SC, 2008.

Search CrossRef
Ramachandran M. Nonlinear Finite Element Analysis of Tweel™ Geometric Parameter Modifications on Spoke Dynamics during High Speed Rolling. Master’s Thesis. Clemson University, Clemson, SC, 2008.

Search CrossRef
Yue H. X., Zhao Y. Q. Nonlinear finite element analysis of a new safety wheel. China Mechanical Engineering, Vol. 23, Issue 11, 2012, p. 1380-1385.

Search CrossRef
Wang W., Zhao Y. Q., Huang C., et al. Modeling and trafficability analysis of new mechanical elastic wheel. China Mechanical Engineering, Vol. 24, Issue 6, 2013, p. 724-729.

Search CrossRef
Rhyne T. B., Cron S. M. Development of a non-pneumatic wheel. Tire Science and Technology, Vol. 34, Issue 3, 2006, p. 150-169.

Search CrossRef

Cited by

Study on the influence of material hardness on the performance of V-shaped non-pneumatic tyres

(2024)

Multi-Material Metamaterial Topology Optimization to Minimize the Compliance and the Constraint of Weight: Application of Non-Pneumatic Tire Additive-Manufactured with PLA/TPU Polymers

Shokouh Dezianian | Mohammad Azadi

(2023)

Structural design and characteristics of a non-pneumatic tire with honeycomb structure

Liguo Zang | Xingyu Wang | Pengwei Yan | Zhendong Zhao

(2022)

Force transmission performance for a novel deformation wheel with crank slider mechanism

(2020)

About this article

Received

17 March 2016

Accepted

18 August 2016

Published

30 September 2016

SUBJECTS

Vibration in transportation engineering

DOI

https://doi.org/10.21595/jve.2016.16988

Keywords

mechanical elastic wheel

non-pneumatic tire

vibration performance analysis

the impulse input experiment

Acknowledgements

This work is partially supported by the National Science Foundation of China (Grant No. 51305175), the National Science Foundation of JiangSu Province (Grant No. BK2012586), the National Science Foundation of Jiangsu University of Technology (Grant No. KYY14041), the 333 Project of Jiangsu Province (BRA2015365) and Jiangsu Province “Six Personnel Peak” Fund Projects (Grant No. 2012-ZBZZ-023) and (Grant No. 2013-ZBZZ-039). The authors gratefully acknowledge the helpful comments and suggestions of the reviewers, which have improved the presentation.

Author Contributions

Wang Wei – vibration performance analysis of vehicle in the impulse input experiment. Zhu Kai – MEW structure analysis. Bei Shaoyi – establishment of finite element model. Zhang Lanchun – comparative analysis of the experiment results. Wang Yongzhi vehicle ride quality simulation comparison.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2019 03 31

Integrated yaw and rollover stability control of an off-road vehicle with mechanical elastic wheel

Haiqing Li, Youqun Zhao, Fen Lin, Han Xu

Research article

2018 03 31

Design and dynamic testing of a roller coaster running wheel with a passive vibration damping system

Piotr Gierlak, Dariusz Szybicki, Krzysztof Kurc, Andrzej Burghardt, Dawid Wydrzyński, Radosław Sitek, Marek Goczał

Research article

2017 09 30

Numerical optimization for vibration and noise of the wheel based on PSO-GA method

Yi Ji, Hai Jun Fu, Kun Hua Chen

Research article

2017 03 31

A novel tread model for tire modelling using experimental modal parameters

Zhen-feng Wang, Ming-ming Dong, Wei-peng Zhao, Liang Gu

W. Wei, Z. Kai, B. Shaoyi, Z. Lanchun, and W. Yongzhi, “Vibration performance analysis of vehicle with the non-pneumatic new mechanical elastic wheel in the impulse input experiment,” Journal of Vibroengineering, Vol. 18, No. 6, pp. 3970–3980, Sep. 2016, https://doi.org/10.21595/jve.2016.16988

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2016.16988
UR  - https://doi.org/10.21595/jve.2016.16988
TI  - Vibration performance analysis of vehicle with the non-pneumatic new mechanical elastic wheel in the impulse input experiment
T2  - Journal of Vibroengineering
AU  - Kai, Zhu
AU  - Wei, Wang
AU  - Shaoyi, Bei
AU  - Lanchun, Zhang
AU  - Yongzhi, Wang
PY  - 2016
DA  - 2016/09/30
PB  - JVE International Ltd.
SP  - 3970-3980
IS  - 6
VL  - 18
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Kai_2016,
	doi = {10.21595/jve.2016.16988},
	url = {https://doi.org/10.21595/jve.2016.16988},
	year = 2016,
	month = {sep},
	publisher = {{JVE} International Ltd.},
	volume = {18},
	number = {6},
	pages = {3970--3980},
	author = {Zhu Kai and Wang Wei and Bei Shaoyi and Zhang Lanchun and Wang Yongzhi},
	title = {Vibration performance analysis of vehicle with the non-pneumatic new mechanical elastic wheel in the impulse input experiment},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]Z. Kai, W. Wei, B. Shaoyi, Z. Lanchun, and W. Yongzhi, “Vibration performance analysis of vehicle with the non-pneumatic new mechanical elastic wheel in the impulse input experiment,” Journal of Vibroengineering, vol. 18, no. 6, pp. 3970–3980, Sep. 2016, doi: 10.21595/jve.2016.16988.

Copy IEEE

Copied to clipboard!

Kai, Zhu, Wang Wei, Bei Shaoyi, Zhang Lanchun, and Wang Yongzhi. “Vibration Performance Analysis of Vehicle with the Non-Pneumatic New Mechanical Elastic Wheel in the Impulse Input Experiment.” Journal of Vibroengineering 18, no. 6 (September 30, 2016): 3970–80. https://doi.org/10.21595/jve.2016.16988.

Copy Chicago

Copied to clipboard!

Vibration performance analysis of vehicle with the non-pneumatic new mechanical elastic wheel in the impulse input experiment

Abstract

1. Introduction

2. MEW structure analysis

2.1. The structure of new mechanical elastic wheel

2.2. The working principle of new mechanical elastic wheel

3. Finite element modeling of MEW

3.1. Establishment of Finite Element Model

3.2. Nonlinear characteristic of MEW

3.3. Validation of Finite Element Model

4. Vibration performance analysis of Vehicle in the impulse input experiment

4.1. Experiment method

4.2. Comparative analysis of the experiment results

5. Vehicle ride quality simulation comparison

6. Conclusions

References

Cited by

About this article

Related Articles