Fluctuation characteristics and rolling control for an underactuated spherical underwater exploration robot

Li, Yansheng; Yang, Meimei; Sun, Hanxu; Liu, Zhimin

doi:10.21595/jve.2016.17105

Journal of Vibroengineering

Browse Journal

Submit article

Published: 31 March 2017

Check for updates

Fluctuation characteristics and rolling control for an underactuated spherical underwater exploration robot

Yansheng Li¹

Meimei Yang²

Hanxu Sun³

Zhimin Liu⁴

^{1, 2}School of Advanced Manufacturing Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, China

^{3, 4}Institute of Automation, Beijing University of Posts and Telecommunications, Beijing 100876, China

Corresponding Author:

Meimei Yang

Cite the article Download PDF

Downloads 1453

WoS Core Citations 1

CrossRef Citations 2

Abstract

Compared with other underwater exploration robots, Spherical underwater robot has an outstanding advantage for the underwater exploration, whose spherical shell has the excellent resiliency to protect the internal electronic components. In addition, this steering resistance is very small to move flexibly. In this paper, a type of spherical underwater robot with the pendulums and a propeller was studied on moving at the water bottom in a rolling manner. The structure and force were analyzed to understand that the hydrodynamic force’s affection on the robot’s rolling at the water bottom. A mathematical model was established with the mass parameters and speeding parameters. The virtual simulation environment was established in Adams software. Furthermore, the coupling fluctuation characteristics of the speed, swing angle and the torque were studied by the simulation and the experiment in a pool. The study proved that this robot not only can use the propeller to move in water, but also can roll at the water bottom by driving the spherical shell. Especially, the result also can be obtained that the robot can roll at water bottom stably by increasing the pendulum mass and lowering the motor speed.

1. Introduction

In recent years, AUV has got much attention in many fields and attracted more and more researchers [1-3]. And, movement flexibility and environmental compatibility are important indicators for an underwater exploration robot [4-6]. Compared with other types of robots, Spherical robot has great advantages in the movement flexibility and environmental compatibility [7-12]. The symmetrical spherical shell can withstand greater pressure and reduce the steering resistance. A kind of underwater spherical robot was developed, ODIN (1991), which is equipped with eight propellers, and every two propellers are assigned together as a group, which can make ODIN move flexibly in a task [13-15]. An underwater spherical robot was developed, URIS (2003), which was equipped with four external propellers [16]. In 2012, a new type of spherical robot was developed with three jetting-water devices and six servo motors, which can change the directions of jetting water [17-19]. And the movement analysis in water was deeply studied for these spherical underwater robots. But these robots did not have the movement ability in the water bottom. So, when the robot moved through underwater propeller, the disturbance from the propeller would affect the collection of samples. Hanxu Sun et al. (2008) designed a spherical robot with heavy pendulum, which can achieve the flexible movement on land [20, 21]. In 2010, a new underwater robot BYSQ-2 was developed with a single propeller [22, 23]. Yansheng Li et al. (2014) studied the hydrodynamic forces and underwater fluctuation characteristics of BYSQ-2 robot [24]. But the features of rolling in the bottom are not fully understood and mastered. So, the analysis for the rolling characteristics is very necessary to improve the underwater environment adaptability. This paper showed the rolling fluctuation characteristics for the sphere robot to expand its movement stability.

This article is organized as follows. In Section 2, the physical model for the robot is introduced, which can move in water by a propeller or in water bottom by rolling. In Section 3, the dynamic equation of rolling is established by Newton Euler method. It is found that the mass and the motor speed are the important parameters for the stably rolling of the underwater robot. In Section 4, the characteristics and influencing factors of coupling fluctuation are analyzed and summarized by building a virtual environment in ADAMS software. In Section 5, an experiment was carried out to demonstrate the ability of stable rolling for the spherical underwater robot. Section 6 provides the conclusions, along with some remarks on future research.

2. Structure and equivalent model

One propeller is designed in the conduit of BYSQ-2 robot, which can provide the thrust for moving in water. And the pendulums locate in both sides of the conduit, which are protected by the spherical shell of the robot. And the conduit is fixed with the spherical shell, which is perpendicular to the short axis. Both the conduit and spherical shell can not only rotate around the long axis, but also rotate around the short axis. So, the robot can roll freely at the water bottom by the motor driving the pendulums. The electronic components are all installed in the spherical glass fiber shell. The main structures of the robot include the spherical shell 1, the conduit 2, the propeller 3, the short axis 4, the pendulum 5 and the rolling motor 6. The physical structure is shown in Fig. 1(a), 1(b). The simplified diagram of rolling at the water bottom is shown in Fig. 1(c).

Fig. 1Model of the robot’s structure and driving forces

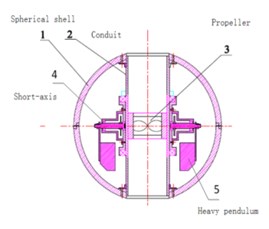
a)

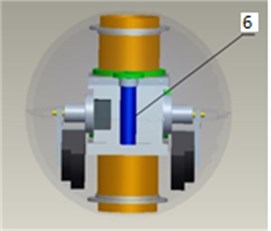
b)

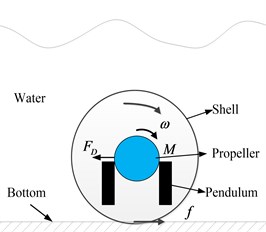
c)

According to the conditions of the actual environment and physical structure, two assumptions are made to analyze the rolling characteristics at the water bottom and establish the dynamic model of the robot. Firstly, spherical robot system is simplified to the weight section and the spherical shell portion. The qualities of the components what are fixed with the heavy pendulum mechanism together are concentrated equivalently in the center of the pendulum. And the qualities of the components what fixed on the spherical shell together are concentrated equivalently in the center of the spherical shell. Secondly, according to the symmetrical design, the rotational inertia’s spindle of the spherical shell that includes the structures fixed with the spherical shell goes through the center of the spherical robot.

3. Establish dynamic equations

Spherical robot rolls at the water bottom and its water resistance is not negligible. Because of the buoyancy’s effect, the supportive force between the robot and the water bottom will be reduced. Furthermore, when the robot rolls at the water bottom, the friction will be also reduced between the spherical shell and the bottom. To determine the effect parameters, a model must be firstly established to describe the dynamics of the spherical robot. In the rolling state at the bottom, as the research object, the force diagram of the spherical shell is shown in Fig. 2.

As shown in Fig. 2, the spherical robot is rolling at the water bottom. At the contact point between the spherical shell at the bottom, there are a friction force $f$ and a supportive force $N$ , which are a pair of interactive forces. Furthermore, the water resistance force $F_{D}$ and the buoyancy $B$ are applied to the spherical shell, which are produced by the water. The horizontal force $F_{x}$ , the vertical force $F_{y}$ and the rotational torque $M$ are also applied to the spherical shell portion of the robot, which are produced by the internal pendulum mechanism. And, the spherical shell structure itself is also affected by gravity $G$ . The parameter $R$ is the maximum radius of the robot. And, the parameter $ω$ is the rolling angular velocity of the robot. The parameter $m_{1}$ is the mass of the robot. The parameter $λ$ is the additional mass factor of the robot. The parameter $v$ is the velocity of the robot. The parameter $J$ is the moment of inertia of the spherical shell. According to Newton Euler’s theorem, the dynamic equations of the spherical shell rolling at the water bottom can be obtained as shown in Eq. (1):

1

\{\begin{array}{l} f + F_{x} - F_{D} = (m_{1} + λ) \dot{v}, \\ B + F_{y} + N - m_{1} g = 0, \\ M - f R = J \dot{ω} . \end{array}

Similarly, in addition to part of a spherical shell, the internal pendulum mechanism should be also analyzed in order to obtain a complete dynamic system equations of the robot. The coordinate origin of the rotating reference system is set in the center of the sphere spherical robot. In order to removal the influences of the Coriolis force, the rotating axis of the heavy pendulum is also set in the center of the sphere spherical robot. The force diagram of the pendulum is shown in Fig. 3.

Fig. 2Force diagrams of the spherical shell rolling at the water bottom

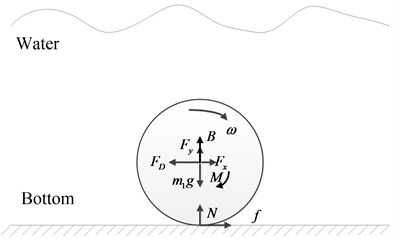
Fig. 3Force diagrams of the internal pendulum mechanism

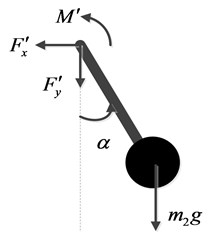
As shown in Fig. 3, driven by a motor, the pendulum swings forward, when the robot rolls forward at the water bottom. The horizontal force $F_{x}^{'}$ , the vertical force $F_{y}^{'}$ and the rotational torque $M^{'}$ are applied to the internal pendulum mechanism portion of the robot, which are produced by the spherical shell. And, the pendulum structure itself is also affected by gravity. The parameter $m_{2}$ is the mass of the pendulum. The parameter $l$ is the length of the pendulum. And, the parameter $α$ is the swing angle of the pendulum. According to Newton Euler’s theorem, the dynamic equations of the pendulum swing can be obtained as shown in Eq. (2):

2

\{\begin{array}{l} {F_{x}}^{'} = - m_{2} \dot{v} - m_{2} l \ddot{α} c o s α + m_{2} l {\dot{α}}^{2} s i n α, \\ {F'}_{y} + m_{2} g = - m_{2} (l \ddot{α} s i n α + l {\dot{α}}^{2} c o s α), \\ M^{'} = m_{2} l^{2} \ddot{α} - m_{2} g l s i n α . \end{array}

In Eqs. (1) and (2), the horizontal $F_{x}$ and $F_{x}^{'}$ , the vertical force $F_{y}$ and $F_{y}^{'}$ , the rotation moment $M$ and $M^{'}$ , are the paired interaction forces. According to Newton’s third law, these three pairs of forces respectively are equal in size and opposite in direction. According to Eq. (1) and (2), the complete dynamic equations of the robot rolling at the water bottom can be obtained as shown in Eq. (3):

3

\{\begin{array}{l} (m_{1} + m_{2} + λ) \dot{v} + F_{D} - f + m_{2} l \ddot{α} c o s α - m_{2} l {\dot{α}}^{2} s i n α = 0, \\ B + N - (m_{2} + m_{1}) g - m_{2} l {\dot{α}}^{2} c o s α - m_{2} l \ddot{α} s i n α = 0, \\ J \dot{ω} + f R - m_{2} l^{2} \ddot{α} + m_{2} g l s i n α = 0 . \end{array}

It is supposed that the balancing mass $Δ m$ is the extra mass to ensure that the gravity of the robot is greater than the buoyancy $B$ of the water, when the spherical robot is rolling at the water bottom. The balancing mass $Δ m$ together with the frictional force $f$ can be expressed as Eq. (4):

4

\{\begin{array}{l} Δ m = \frac{B - m_{1} g - m_{2} g}{g}, \\ f = μ N . \end{array}

According to Eqs. (3) and (4), the complete dynamic equations with the $Δ m$ parameter of the robot rolling at the water bottom can be obtained as shown in Eq. (5):

5

\{\begin{array}{l} J \dot{ω} + μ R m_{2} l {\dot{α}}^{2} c o s α + μ R m_{2} l \ddot{α} s i n α - μ R Δ m g - m_{2} l^{2} \ddot{α} + m_{2} g l s i n α = 0, \\ \begin{array}{l} (m_{1} + m_{2} + λ) \dot{v} + F_{D} - μ R m_{2} l {\dot{α}}^{2} c o s α - μ R l \ddot{α} s i n α \\ + μ Δ m g + m_{2} l \ddot{α} c o s α - m_{2} l {\dot{α}}^{2} s i n α = 0 . \end{array} \end{array}

When the spherical robot is rolling at the water bottom, the swing of the pendulum is driven by a torque of the pendulum motor, whose reaction torque can drive the spherical shell to roll forward. In fact, the rolling angular velocity $ω$ of the robot is related to the rotational angle $θ$ of the motor and the swing angle $α$ of the pendulum. So, their constraint relationship can be obtained as shown in Eq. (6):

6

θ = ω t + α .

According to Eq. (5) and (6), the complete dynamic equations of the robot rolling at the water bottom also can be obtained as shown in Eq. (7):

7

\{\begin{array}{l} J \dot{ω} + μ R m_{2} l {(\dot{θ} - ω)}^{2} c o s (θ - ω t) + μ R m_{2} l (\ddot{θ} - \dot{ω}) s i n (θ - ω t) \\ - μ R Δ m g - m_{2} l^{2} (\ddot{θ} - \dot{ω}) + m_{2} g l s i n (θ - ω t) = 0, \\ (m_{1} + m_{2} + λ) \dot{v} + F_{D} - μ R m_{2} l {(\dot{θ} - ω)}^{2} c o s (θ - ω t) - μ R l (\ddot{θ} - \dot{ω}) s i n (θ - ω t) \\ + μ Δ m g + m_{2} l (\ddot{θ} - \dot{ω}) c o s (θ - ω t) - m_{2} l {(\dot{θ} - ω)}^{2} s i n (θ - ω t) = 0 . \end{array}

As shown in Eq. (7): The rolling state of the spherical underwater robot not only relates to the motor rotational angle $θ$ , but also relates to the balancing mass $Δ m$ of the robot.

4. Simulation model and analysis

In order to analyze the impact of the rotation angle $θ$ and the balancing mass $Δ m$ , the ADAMS prototype and virtual environment were built to research the rolling state of the robot at the water bottom under the conditions of the variable parameters. As assumed in Section 2, two portions are made to analyze the rolling characteristics at the water bottom and establish the dynamic model of the robot. Furthermore, the hydrodynamic coefficients are calculated in FLUENT software and the result is imported into ADAMS software as the simulation constraint conditions. Based on the above principles, the virtual simulation model of the robot rolling at the water bottom is shown in Fig. 4.

Fig. 4Virtual simulation model diagram of the robot rolling at the water bottom

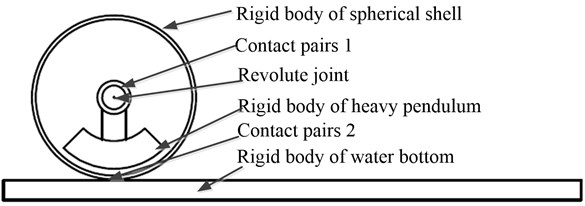
In the virtual simulation environment, a large flat-panel was established as the water bottom, which was set to the fixed rigid body property. The quivalent spherical shell and the equivalent heavy pendulum were also set to the rigid body property and a revolute joint was disposed between the heavy pendulum and spherical shell. This contact pairs were disposed between the two rigid bodies of the spherical shell and the water bottom. Because of the perfect symmetry of the spherical robot, the buoyancy, gravity and hydrodynamics can be applied in the center of the spherical robot. According to the prototype model, the spherical shell diameter $R$ was 400 mm. The water density $ρ$ was set to 1000 kg/m³. The gravitational acceleration g was set to 10 m/s², the buoyancy $B$ was set to 354 N. The hydrodynamic parameter $F_{D}$ was associated with the speed and acceleration parameters of the robot, which also can be disposed on the center of the robot. According to the calculation results in FLUENT software, the drag coefficient associated with quadratic speed items was set to 40 and the drag coefficient associated with the acceleration for additional mass factor is set to 32. $F_{1}$ is a horizontal composition of force in the opposite direction of the robot movement. $F_{2}$ is a vertical composition of force in the same direction of gravity. $F_{1}$ and $F_{2}$ can be set in the center of the spherical robot, which can be expressed as Eq. (8):

8

\{\begin{array}{l} F_{1} = 32.7 \dot{v} + 40 v^{2}, \\ F_{2} = m_{1} g + m_{2} g - 354 . \end{array}

Based on the above spherical robot virtual prototype, this balancing mass $Δ m$ of the spherical robot was set respectively at 10 kg and –10 kg. In order to study the influence of the $Δ m$ parameter, the motor rotating speed remained consistent and the rolling state of the robot at the water bottom was simulated under the conditions of the different $Δ m$ parameters.

As shown in Fig. 5, the $Δ m$ parameter was –10 kg in the left half of the comparison chart. And, the $Δ m$ parameter was +10 kg in the right half of the comparison chart. At the same time, the motor rotating speed remained constant. In these conditions, the fluctuation characteristics of the rolling displacement, the swing angle and the motor torque were simulated, where the differences can be seen that the balancing mass $Δ m$ greatly affected the fluctuation of the rolling process at the water bottom. As shown in Fig. 5(a), the rolling displacement of the spherical robot at the water bottom increased with the balancing mass increasing in the same time period. This displacement increased from 4 m to 6 m in the comparison chart of the rolling displacement. As shown in Fig. 5(b), the swing angle of the heavy pendulum at the water bottom attenuated quickly with the balancing mass increasing. The swing angle of the heavy pendulum converge to 0 in the 5 s in the condition of the balancing mass $Δ m$ +10 kg in the right half of the comparison chart. As shown in Figure 5 (c), the fluctuation of the motor torque discreased obviously with the balancing mass increasing. Based on the above analysis, the conclusion can be drawn that a larger balance mass can increase the stability of the robot rolling at the water bottom.

Furthermore, the balancing mass $Δ m$ remained constant and the motor rotating speed $ω$ is different. The motor rotating speed $ω$ of the spherical robot was set respectively at 0.5 $π$ rad/s and 1.5 $π$ rad/s. In order to study the influence of the $ω$ parameter, the rolling state of the robot at the water bottom was simulated in the condithions of the different $ω$ parameters.

Fig. 5Fluctuation influence on the rolling state under the different Δm parameters

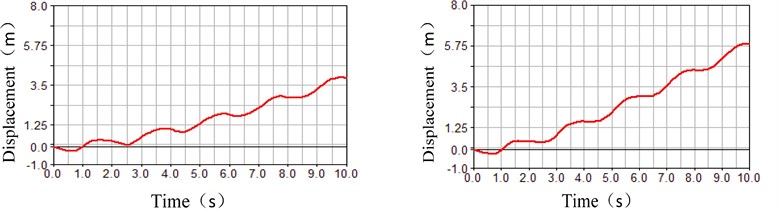
a) Comparison chart of the rolling displacement

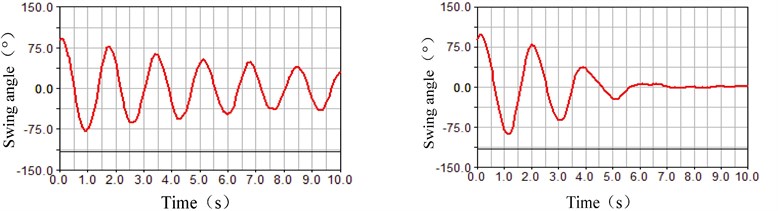
b) Comparison chart of the swing angle

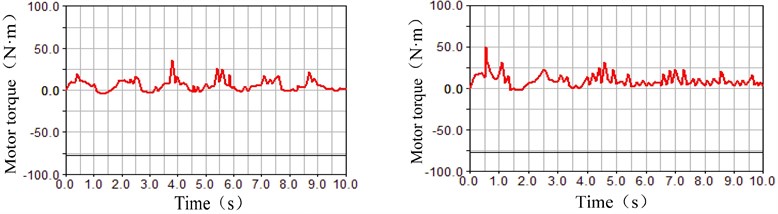
c) Comparison chart of the motor torque

As shown in Fig. 6, the $ω$ parameter was 0.5 $π$ rad/s in the left half of the comparison chart. And, the $ω$ parameter was 1.5 $π$ rad/s in the right half of the comparison chart. At the same time, the balancing mass $Δ m$ remained constant. In these conditions, the fluctuation characteristics of the rolling displacement, the swing angle and the motor torque were simulated, where the differences can be seen that the motor rotating speed $ω$ greatly affected the fluctuation of the rolling process at the water bottom. As shown in Fig. 6(a), the rolling displacement of the spherical robot at the water bottom increased with the motor rotating speed increasing in the same time period. But the relationship was not proportional. As shown in Fig. 6(b), the swing angle of the heavy pendulum at the water bottom did not attenuated quickly with the motor rotating speed increasing. And, the fluctuation became obvious in the 10 s in the condition of the motor rotating speed $ω$ 1.5 $π$ rad/s in the right half of the comparison chart. As shown in Fig. 6(c), the fluctuation of the motor torque became larger than twice with the motor rotating speed increasing. More simulation data was shown in Table 1.

As shown in Table 1, the fluctuation amplitude of the swing angle is maximal and reaches 1.6 rad in the conditions of the total mass 34.1 kg and the motor speed 3 $π$ rad. The fluctuation amplitude of the swing angle is minimal and reaches 0.6 rad in the conditions of the total mass 40.2 kg and the motor speed 1.7 $π$ rad. Based on the above analysis in Fig. 5, Fig. 6 and Table 1, the conclusion can be drawn that a smaller motor rotating speed can increase the stability of the robot rolling at the water bottom. But, a smaller motor rotating speed can also reduce the moving speed of the robot by the rolling manner at the water bottom.

Table 1Simulation data of the robot rolling at the pool bottom

Total mass $m$ (kg)	Motor speed $ω$ (rad/s)	Amplitude of swing angle $α$ (rad)	Time through 3 m $t$ (s)
34.1	1.7 $π$	0.9	7.1
34.1	2.3 $π$	1.4	6.5
34.1	3 $π$	1.6	6.0
37.5	1.7 $π$	0.8	7.0
37.5	2.3 $π$	1.2	6.2
37.5	3 $π$	1.4	5.7
40.2	1.7 $π$	0.6	6.4
40.2	2.3 $π$	0.9	5.5
40.2	3 $π$	1.1	5.0

Fig. 6Fluctuation influence on the rolling state under the different ω parameters

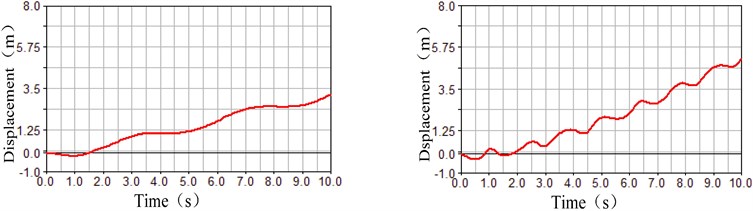
a) Comparison chart of the rolling displacement

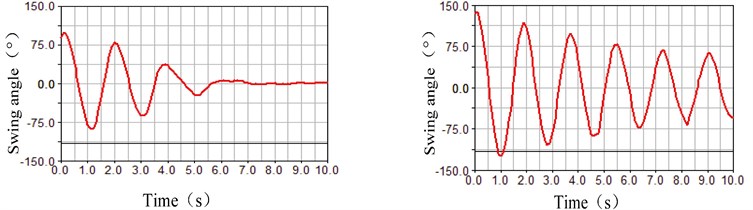
b) Comparison chart of the swing angle

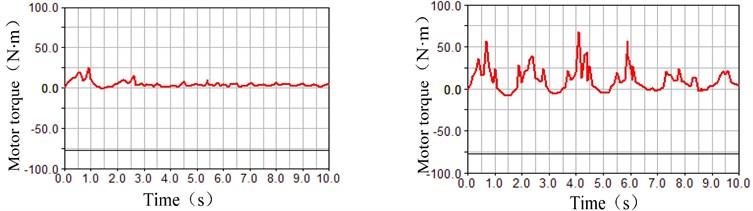
c) Comparison chart of the motor torque

In order to control the motion of spherical robot in the water, Xiaojuan Lan et al (2010) used a fuzzy PID method to suppress the fluctuations of the pendulum, but this method changed the speed value of the motion [23]. Hanxu Sun et al (2014) used a neural network and sliding mode method to control the pitch of the spherical robot, but the neural network initially took lots of time to learn [25]. In this paper, the spherical robot would roll at the water bottom and a direct two-layer sliding surfaces is proposed to control the rolling speed, which is different from the above environment and method in water. Under the rolling condition, the motion equation contains both the rolling constraint and the hydrodynamic constraint, so the governing equations of motion at the water bottom are novel. In the absence of sliding condition, $v = R ω$ and in a low-speed condition, $F_{D} = 40 v^{2}$ . According to Eqs. (1), (2) and (3), the equation of motion for the rolling velocity at the water bottom can be obtained as shown in Eq. (9):

9

\{\begin{array}{l} \dot{v} = f (v) + b_{1} M + D, \\ \ddot{α} = f (α) + b_{2} M, \\ b_{1} = \frac{1}{J + m_{1} R + m_{2} R + λ R}, \\ b_{2} = \frac{- 1}{m_{2} l^{2}}, \\ f (v) = \frac{- 40 R v^{2}}{J + m_{1} R + m_{2} R + λ R}, \\ f (α) = \frac{m_{2} g l s i n α}{m_{2} g l^{2}}, \\ D = \frac{m_{2} l R {\dot{α}}^{2} s i n α - m_{2} l R \ddot{α} c o s α}{J + m_{1} R + m_{2} R + λ R} . \end{array}

The error of rolling velocity is ${\dot{e}}_{1} = v - v_{d}$ , the two primary sliding surfaces and the ultimate sliding surface are designed as follows:

10

\{\begin{array}{l} s_{1} = c_{1} e_{1} + {\dot{e}}_{1}, \\ s_{2} = c_{2} α + {\dot{α}}_{1}, \\ S = β s_{1} + (1 - β) s_{2} . \end{array}

The derivation of the ultimate sliding surface is shown as follows:

11

\dot{S} = β {\dot{s}}_{1} + (1 - β) {\dot{s}}_{2} = β (c_{1} v - c_{1} v_{d} + f (v) + b_{1} M + D - {\dot{v}}_{d})

+ (1 - β) (c_{2} \dot{α} + f (α) + b_{2} M) = β (c_{1} v - c_{1} v_{d} + f (v) - {\dot{v}}_{d})

+ (1 - β) (c_{2} \dot{α} + f (α)) + (β b_{1} + b_{2} - β b_{2}) M + β D .

In order to ensure the ultimate sliding surface converging, the control rate is taken as:

12

M = \frac{- β (c_{1} v - c_{1} v_{d} + f (v) - {\dot{v}}_{d}) + (1 - β) (c_{2} \dot{α} + f (α)) + β D}{(β b_{1} + b_{2} - β b_{2})} .

In order to make the robot system moves along a sliding surface, the additional switching control must be added, so the total control rate includes the following two components:

13

\{\begin{array}{l} M = M_{1} + M_{2}, \\ M_{1} = \frac{- β (c_{1} v - c_{1} v_{d} + f (v) - {\dot{v}}_{d}) + (1 - β) (c_{2} \dot{α} + f (α))}{(β b_{1} + b_{2} - β b_{2})}, \\ M_{2} = - η s g n (S) . \end{array}

The goal of designing controller is to control the rolling velocity, while the swing angle of heavy pendulum is as small as possible. LYAPUNOV function is used to prove the ultimate sliding surface is the stability:

14

V = \frac{1}{2} S^{2},

15

\dot{V} = S (\frac{β D}{(β b_{1} + b_{2} - β b_{2})} - η s g n (S)) .

Because $D < \tilde{D}$ is bounded and $\dot{V} < 0$ :

16

η > |\frac{β \tilde{D}}{(β b_{1} + b_{2} - β b_{2})}| .

$S$ is bounded and asymptotic convergence, and two sliding surfaces are built:

17

\{\begin{array}{l} S_{1} = β_{1} s_{1} + (1 - β_{1}) s_{2}, \\ S_{2} = β_{2} s_{1} + (1 - β_{2}) s_{2} . \end{array}

The difference between the two sliding surfaces is integrated:

18

\int_{0}^{\infty} (S_{1} - S_{2}) d t = (β_{1} - β_{2}) \int_{0}^{\infty} (s_{1} - s_{2}) d t < \infty .

According to BARBALAT theorem, $\underset{t \to \infty}{l i m} (s_{1} - s_{2}) = 0$ , the sum between the two sliding surfaces is integrated:

19

\int_{0}^{\infty} (S_{1} + S_{2}) d t = (β_{1} + β_{2}) \int_{0}^{\infty} (s_{1} - s_{2}) d t + 2 \int_{0}^{\infty} s_{2} d t < \infty .

According to BARBALAT theorem, $\underset{t \to \infty}{l i m} s_{2} = 0$ , and in a similar way, $\underset{t \to \infty}{l i m} s_{1} = 0$ . The two primary sliding surfaces and the ultimate sliding surfaces are asymptotic convergence, so the designed controller is stable, which can realize the rolling at the water bottom for the robot stably.

5. Rolling experiment at the water bottom

In this paper, a kind of spherical robot was studied mainly to collect the underwater information. And there was an advantage that the robot can move at the water bottom in a rolling manner, compared with other underwater robots. In this section, it would be proved that the studied spherical underwater robots have the ability to roll at the water bottom through the rolling experiment as shown in Fig. 7.

Fig. 7Experimental picture of the robot rolling at the pool bottom

The motor rotational angle $θ$ and the balancing mass $Δ m$ of the robot would affect the rolling state of the spherical underwater robot as shown in Table 1. A pool of length 3 m, width 2 m and height 0.5 m was used as the experimental test site for the spherical underwater robot. During the rolling experiment, the recorded data included the robot’s motor speed $ω$ , the robot's moving displacement $s$ , the robot’s moving time $t$ and the robot’s total mass $m$ . In each group of experimental parameters, the experiment was made 5 times to get the robot’s moving data. And the average value was recorded. The rolling experiment of the underwater robot was photographed as shown in Fig. 7. The rolling test data of the underwater robot was recorded as shown in Table 2.

Table 2Experimental data of the robot rolling at the pool bottom

Total mass $m$ (kg)	Motor speed $ω$ (r/min)	Moving displacement $s$ (m)	Moving time $t$ (s)
34.1	50	3	7.6
34.1	70	3	6.8
34.1	90	3	6.1
37.5	50	3	7.2
37.5	70	3	6.6
37.5	90	3	5.8
40.2	50	3	6.5
40.2	70	3	5.8
40.2	90	3	5.2

According to the rol1ing experimental of the underwater robot in Table 2, in the conditions of the mass $m$ 34.1 kg and the motor rotating speed $ω$ 50 r/min, the rolling speed of the robot was Minimal. Conversely, with the total mass and the motor rotating speed of the robot increasing, the rolling speed also increased. In the conditions of the mass $m$ 40.2 kg and the motor rotating speed $ω$ 90 r/min, the maximum rolling speed can reach 0.6 m/s. However, in the conditions of the greater motor rotating speed, the rolling speed of the underwater robot increased slowly with the total mass increasing rapidly. Even the sliding phenomenon of the robot occured at the water bottom. And the rolling speed was difficult to reach more than 0.6 m/s. The $λ$ , $F_{d}$ , $R$ and $l$ parameters in Eq. (3) was related to the size of the structure of the robot and remained constant. It can be obtained that the water resistance term and the friction term becomed large with the robot rolling speed v increasing. When the friction force reached a maximum, the robot started to slip at the water bottom. The relative sliding between the spherical shell and the water bottom make the robot rolling speed remain unchanged. On the other hand, the heavy pendulum swing inside the robot would affect the bottom's supportive force $N$ in the vertical direction, which would change the friction term and cause the fluctuations of the robot rolling at the water bottom in the horizontal direction.

6. Conclusions

As a kind of underactuated spherical underwater robot, it not only can use the propeller to move in the water, but also can drive the spherical shell to roll at the water bottom. The robot can move flexibly and stably, which is beneficial to a long-term observation at the water bottom. This paper researched the fluctuation characteristics of the robot moving in a rolling manner. Firstly, two important influencing parameters was proposed by building a mathematical model of the spherical robot rolling at the water bottom. Secondly, on the basis of building a virtual prototype simulation model, the fluctuation features of the spherical robot rolling at the bottom were analyzed and summarized in the conditions of the different parameters of the balancing mass and the motor rotating speed. Finally, the rolling experiments were carried. And the results showed that the underwater robot had a stable and excellent rolling ability at the water bottom. At the same time,the maximum rolling speed was also obtained.

Several main conclusions can be drawn as follows according to the above analysis of the simulation and experiment.

• The balance mass and the motor rotating speed is the critical parameters to affect the fluctuations of the robot rolling at the water bottom based on the established mathematical model.

• Increasing the balancing mass and reducing the motor rotating speed can suppress the fluctuations of the robot rolling at the water bottom based on the virtual simulation in ADAMS software.

• The robot can roll stably at the water bottom, whose maximum rolling speed is associated with the friction force of the water bottom based on the rolling experiment.

According to the above conclusions, it is necessary to increase the robot’s total mass to reduce the coupling fluctuation and improve the stability of the robot. And it is also important to lower reasonably the motor rotating speed for suppressing the fluctuations, although this is not a good idea. So, a motor rotating controller of the robot will be designed to suppress the rolling fluctuation and improve the rolling speed at the water bottom in future.

References

The Navy Unmanned Undersea Vehicle (UUV) Master Plan. U.S. Department of the Navy, 2004.

Search CrossRef
Houston S., Pkwy S. Remotely Operated Vehicles of the World – 9th Edition. Oilfield Publications Limited, USA, 2000.

Search CrossRef
Storkersen N., Kristensen J., Indreeide A., Seim J., Glancy T. Hugin-UUV for seabed surveying. Sea Technology, Vol. 39, Issue 2, 1998, p. 99-104.

Search CrossRef
Naylies I. The Sensory Requirement of a PC Controlled AUV. Master’s Thesis, Offshore Technology Centre, Cranfield University, 2000.

Search CrossRef
Bachmayer R., Leonard N. E., Graver J., Fiorelli E., BhaRa E., Paley D. Underwater gliders: recent developments and future applications. Proceedings of International Symposium on Underwater Technology, Taipei Taiwan, 2004, p. 195-200.

Search CrossRef
Jason E., Meyer N. Dynamics modeling and performance evaluation of an autonomous underwater vehicle. Ocean Engineering, Vol. 31, Issues 14-15, 2004, p. 1835-1858.

Publisher
Shu-xin W., Xiu-jun S., Yan-hui W., Jian-guo W., Xiao-ming W. Dynamic modeling and motion simulation for a winged hybrid-driven underwater glider. China Ocean Engineering, Vol. 1, Issue 25, 2011, p. 97-112.

Publisher
Watson Simon A., Crutchley Dominic J. P., Green Peter N. The design and technical challenges of a micro-autonomous underwater vehicle (μAUV)*. Proceedings of the IEEE International Conference on Mechatronics and Automation, Beijing, China, 2011, p. 567-572.

Publisher
Watson Simon A., Green Peter N. A de-coupled vertical controller for micro-autonomous underwater vehicles (μAUV)*. Proceedings of the IEEE International Conference on Mechatronics and Automation, Beijing, China, 2011, p. 561-566.

Publisher
Yue C., Guo S., Shi L. Hydrodynamic analysis of the spherical underwater robot SUR-II. International Journal of Advanced Robotic Systems, Vol. 10, Issue 3, 2013, p. 119-134.

Publisher
Pan S., Shi L., Guo S. A Kinect-based real-time compressive tracking prototype system for amphibious spherical robots. Sensors, Vol. 15, Issue 4, 2015, p. 8232-8252.

Publisher
He Y., Shi L., Guo S., et al. Preliminary mechanical analysis of an improved amphibious spherical father robot. Microsystem Technologies, Vol. 99, Issue 6, 2015, p. 1-16.

Search CrossRef
Choi H. T., Hanai A., Choi S. K., Yuh J. Development of an underwater robot, ODIN-III. IEEE International Conference on Intelligent Robots and Systems, 2003, p. 836-841.

Publisher
Do K. D., Jiang Z. P., Pan J., Nijmeijer H. Global output feedback universal controller for stabilization and tracking of underactuated ODIN-an underwater vehicle. Proceedings of the IEEE Conference on Decision and Control, 2002, p. 504-509.

Publisher
Antonelli G., Chiaverini S., Sarkar N., West M. Adaptive control of an autonomous underwater vehicle: experimental results on ODIN. IEEE Transactions on Control Systems Technology, Vol. 9, Issue 5, 2001, p. 756-765.

Publisher
Perez Marc Carreras A Proposal of a Behavior-Based Control Architecture with Reinforcement Learning for an Autonomous Underwater Robot. Ph.D. Dissertation, University of Girona, 2008, p. 47-60.

Search CrossRef
Guo S., Lin X., Tanaka K., Hata S. Modeling of water-jet propeller for underwater vehicles Proceedings of the 2010 IEEE International Conference on Automation and Logistics, 2010, p. 92-97.

Publisher
Guo S., Lin X., Tanaka K., Hata S. Development and control of a vectored water-jet based spherical underwater vehicle. Proceedings of the 2010 IEEE International Conference on Information and Automation, 2010, p. 1341-1346.

Publisher
Xichuan L., Shuxiang G. Development of a spherical underwater robot equipped with multiple vectored water-jet-based thrusters. Journal of Intelligent and Robotic Systems, Vol. 67, 2012, p. 307-321.

Publisher
Yili Z., Hanxu S., Qingxuan J., et al. An omni-directional rolling spherical robot with telescopic manipulator. 2nd International Symposium on Systems and Control in Aerospace and Astronautics, ISSCAA, 2008, p. 1-6.

Search CrossRef
Hou Kang, Sun Hanxu, Jia Qingxuan, et al. Structure design and experiment of a spherical aerial vehicle BYFQ-2. 3rd International Conference on Advanced Materials and Information Technology Processing, AMITP, 2013, p. 519-526.

Publisher
L. Xiaojuan, Hanxu S., Qingxuan J. The hydrodynamic analysis for the underwater robot with a spherical hull. Proceedings of SPIE, The International Society for Optical Engineering, Space Exploration Technologies II, Orlando, USA, 2009, p. 73310E.

Search CrossRef
Xiaojuan L., Hanxu S., Qingxuan J. Principle and dynamic analysis of a new-type spherical underwater vehicle. Journal of Beijing University of Posts and Telecommunications, Vol. 33, Issue 3, 2010, p. 20-23, (in Chinese).

Search CrossRef
Li Yansheng, Sun Hanxu, Zhang Yanheng, Chu Ming, Jia Qingxuan, Lan Xiaojuan Characteristic analysis and fluctuation control for a underactuated spherical underwater robot. Journal of Vibroengineering, Vol. 16, Issue 1, 2014, p. 42-56.

Search CrossRef

Cited by

Power generation performance of a spherical robot with a pendulum in an amphibious environment

Yansheng Li | Meimei Yang | Bo Wei | Yi Zhang

(2022)

Hierarchical sliding mode attitude control of a spherical underwater exploring robot

Zhimin Liu

(2020)

About this article

Received

25 April 2016

Accepted

11 November 2016

Published

31 March 2017

SUBJECTS

Vibration generation and control

DOI

https://doi.org/10.21595/jve.2016.17105

Keywords

spherical robot

underwater robot

rolling characteristics

fluctuation analysis

Acknowledgements

The authors would like to thank the support of China National Natural Science Foundation (51175048) for the research.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 05 18

Dynamic modeling and analysis of a vibration-driven robot driven by a conical dielectric elastomer actuator

Xiaojian Wang, Hongguang Li

Research article

2020 06 30

Hierarchical sliding mode attitude control of a spherical underwater exploring robot

Zhimin Liu

Research article

2019 09 26

Mathematical modeling of the robot motion control system for monitoring deep sea communications

Yuri Zhukov, Ekaterina Khutornaia

Research article

2016 09 30

Finite time point-stabilization of underwater spherical roving robot

Zhimin Liu, Hanxu Sun, Yansheng Li, Qingxuan Jia, Ming Chu

Y. Li, M. Yang, H. Sun, and Z. Liu, “Fluctuation characteristics and rolling control for an underactuated spherical underwater exploration robot,” Journal of Vibroengineering, Vol. 19, No. 2, pp. 1050–1061, Mar. 2017, https://doi.org/10.21595/jve.2016.17105

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2016.17105
UR  - https://doi.org/10.21595/jve.2016.17105
TI  - Fluctuation characteristics and rolling control for an underactuated spherical underwater exploration robot
T2  - Journal of Vibroengineering
AU  - Yang, Meimei
AU  - Li, Yansheng
AU  - Sun, Hanxu
AU  - Liu, Zhimin
PY  - 2017
DA  - 2017/03/31
PB  - JVE International Ltd.
SP  - 1050-1061
IS  - 2
VL  - 19
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Yang_2017,
	doi = {10.21595/jve.2016.17105},
	url = {https://doi.org/10.21595/jve.2016.17105},
	year = 2017,
	month = {mar},
	publisher = {{JVE} International Ltd.},
	volume = {19},
	number = {2},
	pages = {1050--1061},
	author = {Meimei Yang and Yansheng Li and Hanxu Sun and Zhimin Liu},
	title = {Fluctuation characteristics and rolling control for an underactuated spherical underwater exploration robot},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]M. Yang, Y. Li, H. Sun, and Z. Liu, “Fluctuation characteristics and rolling control for an underactuated spherical underwater exploration robot,” Journal of Vibroengineering, vol. 19, no. 2, pp. 1050–1061, Mar. 2017, doi: 10.21595/jve.2016.17105.

Copy IEEE

Copied to clipboard!

Yang, Meimei, Yansheng Li, Hanxu Sun, and Zhimin Liu. “Fluctuation Characteristics and Rolling Control for an Underactuated Spherical Underwater Exploration Robot.” Journal of Vibroengineering 19, no. 2 (March 31, 2017): 1050–61. https://doi.org/10.21595/jve.2016.17105.

Copy Chicago

Copied to clipboard!

Fluctuation characteristics and rolling control for an underactuated spherical underwater exploration robot

Abstract

1. Introduction

2. Structure and equivalent model

3. Establish dynamic equations

4. Simulation model and analysis

5. Rolling experiment at the water bottom

6. Conclusions

References

Cited by

About this article

Related Articles