A semi-analytical method for vibration analysis of thin spherical shells with elastic boundary conditions

Xie, Kun; Chen, Meixia; Li, Zuhui

doi:10.21595/jve.2016.17154

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 June 2017

Check for updates

A semi-analytical method for vibration analysis of thin spherical shells with elastic boundary conditions

Kun Xie¹

Meixia Chen²

Zuhui Li³

^{1, 2, 3}School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, 1037 Luoyu Road, Wuhan 430074, China

Corresponding Author:

Meixia Chen

Cite the article Download PDF

Downloads 2070

WoS Core Citations 8

CrossRef Citations 7

Abstract

A semi-analytical method is proposed to analyze both axisymmetric and asymmetric vibrations of thin opened spherical shells with elastic boundary conditions and discontinuity in thickness. To establish the governing equation, the method is involved in dividing the shell into many narrow strips in meridional direction, and those strips are approximately treated as conical ones with uniform thickness. Flügge shell theory is used to describe the motions of strips and displacement functions are expanded as power series. Artificial springs are employed to restrain displacements at edges so that arbitrary boundary conditions can be analyzed. By assembling all continuity conditions of adjacent strips and boundary conditions, the governing equation is established. In numerical results discussion, many comparisons of frequency parameters of present method and those in literature are firstly presented and they illustrate high accuracy and wide application of present method. Furthermore, influences of elastic boundary conditions, open angle, ratio of thickness to radius and thickness discontinuity on natural frequencies of spherical shells are investigated. Results show that meridinoal and circumferential displacements have obvious effects on natural frequencies, and the influence of thickness discontinuity seriously depends on the location of discontinuity.

1. Introduction

In building roofs, LNG tanks, offshore structures, nuclear power plants and other engineering structures, spherical shells are extensively used. Many times those structures are subjected to various external loads, such as earthquakes and sea waves, and the loads are of serious consequence for the strength and safety. Herein, knowing vibration characteristics plays an important role in design process. To this end, vibrations of spherical shells were investigated in past years and are also attracting attentions of more and more scholars nowadays.

In general, the research method analyzing vibrations of spherical shells can be classified as three categories: analytical method [1-21], numerical method [22-37] and experimental method [38]. For analytical method, selecting appropriate displacement functions is the most important aspect. Although Legendre functions are usually adopted [2, 3, 6-11, 13-15], those functions significantly increase difficulties in solving natural frequencies due to the complex values. Niordson [14, 15] decomposed Legendre functions into real and imagine parts and the frequency equation could be correspondently solved in real number region. However, the form of displacements is uncertain around the critical frequency. Except for Legendre functions, Bessel functions were also used by some scholars, such as Kalnins and Naghdi [1], Hoppmann II [4] and Kalnins [5], to express the displacement functions of spherical shells. However, only shallow spherical shells can be accurately analyzed. Chakrabarti [12] adopted elementary (algebraic) functions to study radial vibrations of spherical shells. Lee [17] employed Chebyshev polynomials and Fourier series to express the displacement functions of spherical caps. Then, Lee [18] used the same method to analyze free vibration a hermetic capsule consisting of one cylindrical shell and two hemispherical shells. Standard Fourier series with auxiliary functions were adopted by Su et al. [19] to express displacement functions of functionally graded spherical shells. Chernobryvko et al. [20] used the eigenmodes of the cantilever beam to approximate eigenmodes of axisymmetric shells and presented natural frequencies of a spherical shell of clamped-free boundary conditions. Excepting two-dimensional shell theory, three-dimensional method was adopted by Chen and Ding [16] and Kang [21] to study vibrations of multi-layered hollow spheres and shallow spherical domes, respectively.

Numerically solving governing equations [22, 23, 30-33] and discretizing spherical shell [24-29, 34-37] are two main numerical methods to analyze vibrations of spherical shells. Zarghamee and Robinson [22] used the Holzer method to analyze free vibrations of spherical shells. Souza and Croll [23] investigated free vibrations of spherical shells by the finite difference method. Artioli and Viola [30] and Tornabene and Viola [31] used the generalized differential quadrature method (GDQ) to evaluate natural frequencies of spherical shells. Simmonds and Hosseinbor [32, 33] adopted a perturbation method to study free and forced vibrations of a closed elastic spherical shell fixed to an equatorial beam. As similar with other shell structures, finite element method [24, 26, 29] and semi-analytic finite element method [27] are the most common discrete methods to study vibrations of spherical shells. By using circular arc to represent the generic segment of the shell of revolution, Singh [25] adopted Bezier polynomials to study free vibrations of shells of revolutions. Piecewise Hermite interpolation polynomial and Fourier approximation were used by Wu and Heyliger [28] to expand approximately unknown displacements and forces in azimuthal and circumferential directions, respectively. By combining the modified variational principle with multi-segment partitioning procedure, Qu et al. [34] studied free and forced vibrations of functionally graded shells of revolution through adopting Fourier series and polynomials to expand the displacements. Choi et al. [35] used the Sylvester-transfer stiffness coefficient method to study free vibrations of axisymmetric shells. Before establishing the governing equation, axisymmetric shells were divided into lots of narrow strips and those strips were treated approximately as conical shells. Naghsh et al. [36] used the meridional finite strip method to investigate free vibrations of general shells of revolution, and natural frequencies of a spherical shell with constant and linearly variable thickness in the meridional direction were presented. Cui et al. [37] proposed a nodal integration model for elastic-static, free vibration and forced vibrations of axisymmetric thin shells by using two-node truncated conical elements.

In most above cited literature, the thickness of shell is uniform and only classic boundary conditions are taken into account. However, in practical engineering applications, boundary conditions may not be fixed in a classic restraint, and a variety of boundary conditions, such as elastic ones, may be encountered. In addition, non-uniform thickness, e.g. continuous variational thickness and stepped thickness, is also widely adopted to efficiently improve structural strength without obviously increasing the weight. At this context, proposing an accurate and efficient method for vibration analysis of thin spherical shells with arbitrary boundary conditions and non-uniform thickness is meaningful.

The main purpose of the paper is to present an approach to analyze free vibrations of thin spherical shells with arbitrary boundary conditions and non-uniform thickness. First, the spherical shell is decomposed into lots of narrow strips, which are approximately treated as conical shells. Then, Flügge thin shell theory is employed to describe equations of motions of those conical strips, and displacement functions are expressed as power series. Finally, the governing equation is established through assembling continuity and boundary conditions. Based on the proposed method, effects of elastic boundary conditions, open angles, thickness discontinuity and other parameters on vibration characteristics of spherical shells are investigated. The present method is believed to include following novelties. It offers an accurate and efficient method to investigate free vibrations of spherical shells with elastic boundary conditions. In addition, it is applicable to deal with both uniform and non-uniform thickness. Last but not least, as spherical shells are coupled with thin cylindrical, conical and/or spherical shells, the continuity conditions between spherical shells and other shells can be accurately satisfied by present method. Vibrations of this kind of coupled structures are rarely studied whereas vibrations of coupled cylindrical-cylindrical, conical-cylindrical and conical-conical shells have been relatively extensively studied.

2. Theoretical formulations

2.1. Basic concept of the semi-analytical method

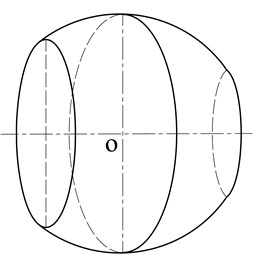
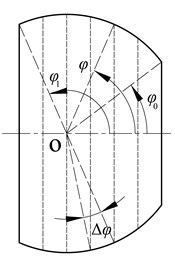
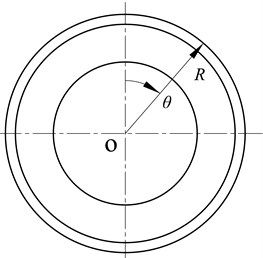
Fig. 1 shows the schematic diagram of a spherical shell with two open angles. The thickness may be constant, stepwise or continuous variational. $φ$ and $θ$ denote the azimuthal and circumferential coordinates in spherical coordinate system. $φ_{0}$ and $φ_{1}$ are the azimuth angles of two edges. In order to establish the governing equation of the spherical shell, the shell is divided into many narrow strips along the short dash lines in Fig. 1(b), and the strips are approximately treated as conical shells. Meanwhile, the thickness of any narrow strip, which may be variational, can be equivalently dealt as constant one when the strips are narrow enough. Radii of two ends of the strip are same as the radii of two circles of edges of the corresponding strip, and the axial length is the axial distance between the two circles. Then, on the basis of Flügge thin shell theory, power series are adopted to expand displacements of conical shells. Consequently, for a particular circumferential mode number, displacements and forces at the cross-section of one strip can be expressed in terms of eight unknown coefficients. Lastly, four continuity conditions of displacements and four equilibrium equations of forces of adjacent two strips are used to assemble those strips to the spherical shell. With the help of boundary conditions, the final governing equation analyzing vibrations of spherical shells is established.

If north and/or south poles are included in the spherical shell, the poles should be cut so that the strip closing to the pole can be treated as truncated conical shells. In addition, the hole must be small enough to avoid big errors. In the following analysis, the azimuth angle of edge is $φ =$ 0.1° for the north pole while the azimuth angle of edge is $φ =$ 179.9° for the south pole. At those added edges, free boundary conditions are adopted.

Fig. 1Schematic diagram of a spherical shell with two edges

a)

b)

c)

2.2. Equations of motion of conical shells

The local coordinate system, displacements and forces of a conical shell are shown in Fig. 2. $x$ is the meridional coordinate and it’s measured from the middle of the strip. $θ$ is the circumferential coordinate and it’s same with that of the spherical shell. $R_{1}$ and $R_{2}$ are the radii of small and large ends, respectively. $R_{0}$ is the mean radius and $R$ is the radius at $x$ . $α$ is the semi-vertex angle. $u$ , $v$ and $w$ are the displacements in meridional, circumferential and normal directions. $β = \partial w / \partial x$ denotes the slope. $M$ is the bending moment resultant, $N$ is the meridional force resultant, and $\bar{S}$ and $\bar{N}$ are the normal and circumferential Kelvin-Kirchhoff shear force resultants, respectively.

Fig. 2Local coordinate system, displacements and forces of a conical shell

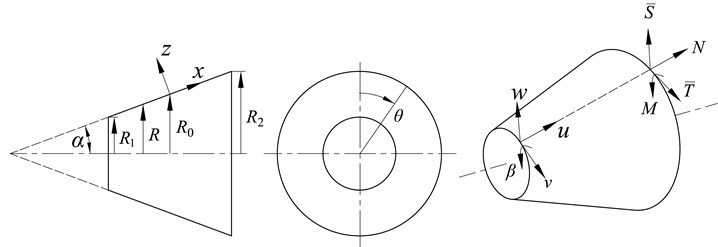
By utilization of Flügge shell theory, equations of motion of a conical shell are [39]:

1

L_{11} u + L_{12} v + L_{13} w - ρ h \frac{\partial^{2} u}{\partial t^{2}} = 0,

L_{21} u + L_{22} v + L_{23} w - ρ h \frac{\partial^{2} v}{\partial t^{2}} = 0,

L_{31} u + L_{32} v + L_{33} w - ρ h \frac{\partial^{2} w}{\partial t^{2}} = 0,

where $h$ and $ρ$ are the thickness and density, respectively. Differential operators $L_{i j}$ ( $i$ , $j =$ 1, 2, 3) can refer to Ref. [40].

For a given circumferential mode number, power series are employed to express displacement functions [41]:

2

u (x, θ, t) = \sum_{p = 0}^{\infty} a_{n, p} x^{p} c o s (n θ) e^{- j ω t},

v (x, θ, t) = \sum_{p = 0}^{\infty} b_{n, p} x^{p} s i n (n θ) e^{- j ω t},

w (x, θ, t) = \sum_{p = 0}^{\infty} c_{n, p} x^{p} c o s (n θ) e^{- j ω t} .

In Eq. (2), the recurrence relations of $a_{n, p}$ , $b_{n, p}$ , $c_{n, p}$ have been detailedly deduced in the authors’ recently opened paper [40]. With the help of the recurrence relations, only eight unknown coefficients, $a_{n, 0}$ , $a_{n, 1}$ , $b_{n, 0}$ , $b_{n, 1}$ , $c_{n, 0}$ , $c_{n, 1}$ , $c_{n, 2}$ , $c_{n, 3}$ , exist in the displacement functions. Omitting subscript $n$ , the displacement functions can be further expressed as:

3

u (x, θ, t) = u \cdot x \cdot c o s (n θ) e^{- j ω t},

v (x, θ, t) = v \cdot x \cdot s i n (n θ) e^{- j ω t},

w (x, θ, t) = w \cdot x \cdot c o s (n θ) e^{- j ω t},

where the vectors $u$ , $v$ , $w$ and $x$ are:

4

u = [u_{1} (x) . . . u_{8} (x)], v = [v_{1} (x) . . . v_{8} (x)], w = [w_{1} (x) . . . w_{8} (x)],

and

5

x = {[a_{0} a_{1} b_{0} b_{1} c_{0} c_{1} c_{2} c_{3}]}^{T} .

In Eq. (4), $u_{i} (x)$ , $v_{i} (x)$ and $w_{i} (x)$ ( $i =$ 1-8) are the base functions.

It must be mentioned that only torsionless axisymmetric modes $(u \neq 0$ , $w \neq 0$ , $v = 0)$ , namely breathing modes, are accounted for in the following analysis. In addition, in view of differences of semi-vertex angles of two adjacent strips, displacements and forces will be considered in the cylindrical coordinate system. Correspondingly, four notations about some displacements and forces are introduced and they are:

6

\tilde{u} = u c o s α_{i} - w s i n α_{i}, \tilde{w} = w c o s α_{i} + u s i n α_{i},

\tilde{N} = N c o s α_{i} - \bar{S} s i n α_{i}, \tilde{\bar{S}} = \bar{S} c o s α_{i} + N s i n α_{i},

where $α_{i}$ is the semi-vertex angle of the $i$ th strip, $\tilde{u}$ and $\tilde{w}$ are the axial and radial displacements, and $\tilde{N}$ and $\tilde{\bar{S}}$ denote axial and radical force resultants, rather than meridional and normal ones.

Substituting the functions of displacements into the expressions of slope and forces (Expressions of force resultants in terms of displacements are given in the Appendix), four displacements and four forces at the cross-section can be expressed as:

7

{[\tilde{u} v \tilde{w} β \tilde{N} \bar{T} \tilde{\bar{S}} M]}^{T} = [\begin{array}{l} [D] \\ [F] \end{array}] \cdot x,

where

8

[D] = [\begin{matrix} {\tilde{u}}_{1} & {\tilde{u}}_{2} & {\tilde{u}}_{3} & {\tilde{u}}_{4} & {\tilde{u}}_{5} & {\tilde{u}}_{6} & {\tilde{u}}_{7} & {\tilde{u}}_{8} \\ v_{1} & v_{2} & v_{3} & v_{4} & v_{5} & v_{6} & v_{7} & v_{8} \\ {\tilde{w}}_{1} & {\tilde{w}}_{2} & {\tilde{w}}_{3} & {\tilde{w}}_{4} & {\tilde{w}}_{5} & {\tilde{w}}_{6} & {\tilde{w}}_{7} & {\tilde{w}}_{8} \\ β_{1} & β_{2} & β_{3} & β_{4} & β_{5} & β_{6} & β_{7} & β_{8} \end{matrix}],

9

[F] = [\begin{matrix} {\tilde{N}}_{1} & {\tilde{N}}_{2} & {\tilde{N}}_{3} & {\tilde{N}}_{4} & {\tilde{N}}_{5} & {\tilde{N}}_{6} & {\tilde{N}}_{7} & {\tilde{N}}_{8} \\ {\bar{T}}_{1} & {\bar{T}}_{2} & {\bar{T}}_{3} & {\bar{T}}_{4} & {\bar{T}}_{5} & {\bar{T}}_{6} & {\bar{T}}_{7} & {\bar{T}}_{8} \\ {\tilde{\bar{S}}}_{1} & {\tilde{\bar{S}}}_{2} & {\tilde{\bar{S}}}_{3} & {\tilde{\bar{S}}}_{4} & {\tilde{\bar{S}}}_{5} & {\tilde{\bar{S}}}_{6} & {\tilde{\bar{S}}}_{7} & {\tilde{\bar{S}}}_{8} \\ M_{1} & M_{2} & M_{3} & M_{4} & M_{5} & M_{6} & M_{7} & M_{8} \end{matrix}] .

In Eqs. (8) and (9), the detailed expressions of $Φ_{i}$ , which represents ${\tilde{u}}_{i}$ , $v_{i}$ , ${\tilde{w}}_{i}$ , $β_{i}$ , ${\tilde{N}}_{i}$ , ${\bar{T}}_{i}$ , ${\tilde{\bar{S}}}_{i}$ and $M_{i}$ , can be readily obtained and they are not given for the sake of brevity.

2.3. Boundary and continuity conditions

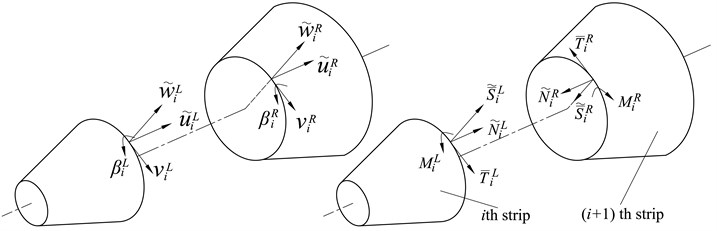
After all strips have been analyzed individually, the strips can be assembled through the continuity conditions. Fig. 3 shows the displacements and forces at the $i$ th junction, namely the junction between the $i$ th strip and ( $i + 1$ )th strip. The continuity conditions of displacements and equilibrium equations of forces are:

10

{\tilde{u}}_{i}^{L} = {\tilde{u}}_{i}^{R}, v_{i}^{L} = v_{i}^{R}, {\tilde{w}}_{i}^{L} = {\tilde{w}}_{i}^{R}, β_{i}^{L} = β_{i}^{R},

11

{\tilde{N}}_{i}^{L} = {\tilde{N}}_{i}^{R}, T_{i}^{L} = T_{i}^{R}, {\tilde{\bar{S}}}_{i}^{L} = {\tilde{\bar{S}}}_{i}^{R}, M_{i}^{L} = M_{i}^{R},

where $L$ and $R$ represent edges of adjacent strips at left side and right side of the $i$ th junction, respectively.

Besides continuity conditions, boundary conditions are also indispensable. Artificial springs are employed to restrain the displacements at the ends, and corresponding equations are:

12

K_{u}^{} u \pm N = 0, K_{v}^{} v \pm \bar{T} = 0, K_{w}^{} w \pm \bar{S} = 0, K_{β}^{} β \pm M = 0,

where, plus sign indicates boundary condition at $φ = φ_{1}$ while minus sign indicates boundary condition at $φ = φ_{0}$ . $K_{u}^{}$ , $K_{v}^{}$ , $K_{w}^{}$ and $K_{β}^{}$ are stiffness constants of artificial springs restraining meridional, circumferential and normal displacements and slop, respectively.

By assigning appropriate values of stiffness constants of artificial springs, both classic and elastic boundary conditions can be analyzed. In the following analysis, the stiffness constant is set as 0 if the corresponding displacement is free or is assigned as a large value (10¹⁶ N/m) if the corresponding one is fixed, e.g. $K_{u}^{} = K_{v}^{} = K_{w}^{} = K_{β}^{} = 0$ for free boundaries $(F),$ $K_{u}^{} = K_{v}^{} = K_{w}^{} = K_{β}^{} =$ 10¹⁶ N/m for clamped boundaries $(C),$ and $K_{u}^{} = K_{β}^{} =$ 0 and $K_{v}^{} = K_{w}^{} =$ 10¹⁶ N/m for hinged boundaries ( $H$ ).

Fig. 3Displacements and forces of adjacent strips

2.4. Final governing equation

Assuming that a spherical shell is decomposed into $P$ individual narrow strips, 8 $P$ unknown coefficients need to be solved for a given circumferential mode number. The final governing equation, Eq. (13), can be obtained by assembling all continuity conditions and boundary conditions in matrix form:

13

K X = 0,

where $X = {[[x_{1}]^{T}, [x_{2}]^{T}, . . ., [x_{P}]^{T}]}^{T}$ is a $8 P \times 1$ vector of the unknown coefficients of all strips, and the expression of $K$ is:

14

K = [\begin{matrix} [B_{1} (- l_{1} / 2)] \\ [D_{1} (l_{1} / 2)] & - [D_{2} (- l_{2} / 2)] \\ [F_{1} (l_{1} / 2)] & - [F_{2} (- l_{2} / 2)] \\ [D_{2} (l_{2} / 2)] & - [D_{3} (- l_{3} / 2)] \\ [F_{2} (l_{2} / 2)] & - [F_{3} (- l_{3} / 2)] \\ \dots & \dots \\ \dots & \dots \\ [D_{P - 1} (l_{P - 1} / 2)] & - [D_{P} (- l_{P} / 2)] \\ [F_{P - 1} (l_{P - 1} / 2)] & - [F_{P} (- l_{P} / 2)] \\ [B_{P} (l_{P} / 2)] \end{matrix}],

where $l_{i} (i = 1 : P)$ is the meridional length of the $i$ th strip. By assigning appropriate dimension and material parameters of the corresponding strip, values of the elements in $[D_{i}]$ and $[F_{i}]$ are obtained through Eqs. (8, 9). $[B_{1}]$ and $[B_{P}]$ depend on the boundary conditions of two edges, and the general expressions are:

15

[B_{i}^{}] = [T^{s}] \cdot [T^{c}] \cdot [D_{i}^{}] \pm [T^{c}] \cdot [F_{i}^{}], i = 1, P,

where $[T^{s}]$ is the matrix about stiffness constants of artificial springs, $[T^{c}]$ denotes the transformation matrix about the notations introduced in Eq. (6), and their detailed expressions are:

16

[T^{s}] = d i a g (K_{u}^{}, K_{v}^{}, K_{w}^{}, K_{β}^{}),

17

[T^{c}] = [\begin{matrix} c o s α_{i} & 0 & s i n α_{i} & 0 \\ 0 & 1 & 0 & 0 \\ - s i n α_{i} & 0 & c o s α_{i} & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] .

Keeping circumferential number $n$ unchanged, $ω$ is increased in an appropriately small step until the sign of the determinant of matrix $K$ changes, and corresponding eigenvalue is roughly obtained. Decreasing the step and repeating the same process, the eigenvalue, namely natural frequency, can be trapped with the desired accuracy. Meanwhile, substituting the eigenvalue back into Eq. (13) and setting one coefficient in vector $X$ to 1, all the other coefficients can be solved and the corresponding mode shape can be obtained.

3. Numerical results and discussion

In the following analysis, all natural frequencies are expressed as frequency parameters, $Ω = ω R \sqrt{(1 - υ^{2}) ρ / E}$ .

3.1. Convergence and validity

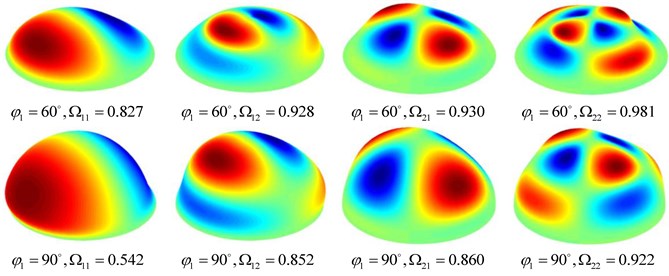
First, the convergence of present method for asymmetric vibrations of a clamped spherical shell with different open angles and ratios of thickness to radius is discussed. Before convergence analysis, a notation, $Δ φ$ , is introduced and it denotes the difference of azimuth angles of two edges of one strip, as shown in Fig. 1. For the sake of brevity, the value of $Δ φ$ is constant for one kind of decomposition, and different values of $Δ φ$ essentially indicate different numbers of strips, e.g. $Δ φ =$ 1° denotes 60 strips as $φ_{1} =$ 60° and 90 strips as $φ_{1} =$ 90°. The influence of the number of strips on frequency parameters is listed in Table 1, and Fig. 4 shows some mode shapes. In the table, $m$ denotes mode number in meridional direction. As $Δ φ$ decreases, frequency parameters rapidly converge, and the ones of $Δ φ =$ 0.5° satisfy the requirement of convergence. More importantly, the difference of frequency parameters of present method and those in the literature is negligible, which demonstrates high accuracy of present method. Furthermore, although the thin shell theory is adopted, present method can still predict accurately natural frequencies as the ratio of thickness to radius $h / R$ reaches 0.05.

Fig. 4Asymmetric mode shapes and frequency parameters Ωnm of the spherical shell with different open angles

The convergence of frequency parameters of axisymmetric modes of a clamped spherical shell is presented in Table 2. Compared with asymmetric modes, the rate of convergence for axisymmetric modes is slower. Some axisymmetric mode shapes are shown in Fig. 5, and it’s seen that the amplitudes of mode shapes have obvious variation at the region closing to the pole, which explains why more strips are required to satisfy the requirement of convergence. It’s further observed that the convergence rate of frequency parameter of the spherical shell with $φ_{1} =$ 30° is obviously slower than the others, which is mainly attributed to higher frequency parameters and similar variations of amplitudes at much smaller region for the same meridional mode. Last but most important, excellent agreement of frequency parameters of present method and literature is observed. That’s to say the axisymmetric vibrations can be also accurately analyzed by present method.

Table 1Convergence of frequency parameters of asymmetric modes of a clamped spherical shell with different open angles (φ0= 0°, υ= 0.3)

$\frac{h}{R}$	$n$	$m$	$φ_{1} =$ 60°					$φ_{1} =$ 90°
			$Δ φ$			Ref. [11]	Ref. [24]	$Δ φ$			Ref. [11]	Ref. [24]
			3°	1°	0.5°	Ref. [11]	Ref. [24]	3°	1°	0.5°	Ref. [11]	Ref. [24]
0.05	1	1	0.919	0.863	0.858	0.859	0.858	0.589	0.566	0.564	0.564	0.563
	1	2	1.304	1.170	1.166	1.087	1.154	0.936	0.906	0.904	0.905	0.903
	2	1	1.034	1.034	1.034	1.034	1.029	0.879	0.879	0.879	0.879	0.879
	2	2	1.142	1.440	1.438	1.125	1.408	1.028	1.027	1.027	1.059	1.029
	3	1	1.170	1.170	1.170	1.184	1.158	0.962	0.962	0.962	0.961	0.959
	3	2	1.764	1.764	1.744	1.307	1.684	1.145	1.144	1.144	1.180	1.136
0.02	1	1	0.868	0.788	0.832	0.833	0.832	0.580	0.530	0.548	0.548	0.548
	1	2	1.002	0.941	0.961	0.962	0.961	0.875	0.843	0.863	0.863	0.863
	2	1	0.950	0.950	0.950	0.950	0.949	0.863	0.863	0.863	0.863	0.862
	2	2	1.052	1.051	1.051	1.085	1.050	0.937	0.937	0.937	0.936	0.936
	3	1	0.990	0.990	0.990	0.991	0.990	0.914	0.914	0.914	0.915	0.914
	3	2	1.130	1.130	1.130	1.157	1.127	0.977	0.977	0.977	0.977	0.977
0.01	1	1	0.851	0.820	0.827	0.827	0.827	0.599	0.539	0.542	0.542	0.542
	1	2	0.941	0.924	0.928	0.928	0.928	0.860	0.850	0.852	0.852	0.853
	2	1	0.930	0.929	0.930	0.925	0.930	0.860	0.860	0.860	0.860	0.860
	2	2	0.981	0.981	0.981	0.981	0.981	0.922	0.922	0.922	0.922	0.922
	3	1	1.062	0.952	0.952	0.949	0.952	0.904	0.904	0.904	0.908	0.904
	3	2	1.010	1.010	1.010	1.006	1.010	0.944	0.944	0.944	0.944	0.944

Table 2Convergence of frequency parameters of axisymmetric modes of a clamped spherical shell with three different open angles (φ0= 0°, h/R= 0.01, v= 0.3)

$m$	$φ_{1} =$ 30°				$φ_{1} =$ 60°				$φ_{1} =$ 90°
	$Δ φ$			Ref. [13]	$Δ φ$			Ref. [13]	$Δ φ$			Ref. [13]
	1°	0.5°	0.25°	Ref. [13]	1°	0.5°	0.25°	Ref. [13]	1°	0.5°	0.25°	Ref. [13]
1	1.132	1.017	0.999	0.998	0.881	0.868	0.868	0.868	0.734	0.726	0.726	0.725
2	1.380	1.305	1.260	1.260	0.973	0.953	0.950	0.950	0.903	0.895	0.895	0.895
3	1.744	1.583	1.536	1.537	1.068	1.026	1.017	1.017	0.949	0.939	0.939	0.939
4	2.358	2.085	1.948	1.948	1.211	1.151	1.131	1.131	0.992	0.976	0.973	0.973
5	3.349	3.012	2.770	2.772	1.434	1.341	1.307	1.308	1.053	1.028	1.021	1.022

To further illustrate high accuracy and wide application of present method, more comprehensive comparisons of frequency parameters are tabulated in Table 3. A spherical shell with four kinds of open angles, three different ratios of thickness to radius and two different boundary conditions are considered. It’s observed that, as the ratio of thickness to radius is small, e.g. $h / R =$ 0.005 and $h / R =$ 0.01, frequency parameters of present method coincide exactly with the ones in literature for all four kinds of open angles. As $h / R$ increases to 0.05, obvious differences can be found for some modes if open angle $φ_{1}$ is small. It’s further found that, for the same circumferential and meridional mode numbers, frequency parameters of the spherical shell with small open angle are obvious larger than those of the spherical shell with large open angle. In addition, classical thin shell theory is employed by present paper while the first-order shear deformation theory is used in [24], and differences of those two theories are negligible at low frequency. All those mentioned reasons lead to obvious differences for some modes when $h / R$ is 0.05. From Table 3, it can be also observed that frequency parameters of the shell with clamped boundary conditions are expectedly larger than those of the shell with hinged boundary conditions, and the frequency parameters increase as the ratio of thickness to radius increases.

Table 3Comparison of frequency parameters of a spherical shell with different open angles and boundary conditions (φ0= 0°, v= 0.3)

$φ_{1}$	$n$	$m$	$C$						$H$
			$h / R =$ 0.005		$h / R =$ 0.01		$h / R =$ 0.05		$h / R =$ 0.005		$h / R =$ 0.01		$h / R =$ 0.05
			Ref. [24]	Present	Ref. [24]	Present	Ref. [24]	Present	Ref. [24]	Present	Ref. [24]	Present	Ref. [24]	Present
30°	1	1	0.968	0.964	1.003	1.001	1.416	1.450	0.963	0.959	1.003	1.001	1.211	1.222
		2	1.037	1.042	1.161	1.165	2.949	3.231	1.037	1.043	1.107	1.110	2.506	2.668
		3	1.155	1.137	1.572	1.575	3.843	3.886	1.113	1.095	1.435	1.436	3.838	3.861
	2	1	0.993	0.993	1.054	1.055	1.954	2.061	0.989	0.990	1.050	1.050	1.627	1.679
		2	1.086	1.087	1.319	1.323	3.952	4.504	1.080	1.080	1.233	1.236	3.437	3.781
		3	1.266	1.268	1.868	1.883	5.878	5.917	1.208	1.209	1.700	1.711	5.822	5.916
	3	1	1.017	1.017	1.125	1.126	2.625	2.857	1.017	1.017	1.102	1.103	2.209	2.345
		2	1.146	1.147	1.518	1.526	4.995	5.902	1.124	1.124	1.400	1.405	4.447	5.063
		3	1.397	1.399	2.202	2.226	7.594	7.669	1.321	1.322	2.008	2.025	7.205	7.669
45°	1	1	0.921	0.920	0.927	0.926	1.020	1.023	0.920	0.919	0.926	0.926	0.973	0.974
		2	0.958	0.958	0.986	0.987	1.589	1.643	0.958	0.958	0.977	0.978	1.403	1.430
		3	0.992	0.987	1.097	1.096	2.508	2.579	0.985	0.980	1.060	1.059	2.350	2.465
	2	1	0.947	0.947	0.969	0.970	1.233	1.250	0.944	0.944	0.967	0.967	1.146	1.155
		2	0.988	0.988	1.053	1.053	2.054	2.167	0.985	0.985	1.048	1.048	1.812	1.879
		3	1.044	1.044	1.202	1.204	3.308	3.647	1.043	1.044	1.155	1.157	2.997	3.245
	3	1	0.960	0.960	0.996	0.996	1.497	1.540	0.958	0.958	0.996	0.996	1.354	1.381
		2	1.009	1.009	1.107	1.108	2.564	2.763	1.007	1.007	1.092	1.093	2.284	2.417
		3	1.077	1.077	1.314	1.318	3.999	4.531	1.074	1.074	1.253	1.256	3.658	4.054
60°	1	1	0.825	0.825	0.827	0.827	0.858	0.858	0.823	0.823	0.823	0.823	0.833	0.833
		2	0.918	0.918	0.928	0.928	1.154	1.166	0.915	0.915	0.921	0.921	1.076	1.081
		3	0.949	0.948	0.983	0.983	1.679	1.737	0.945	0.944	0.971	0.970	1.548	1.588
	2	1	0.922	0.922	0.930	0.930	1.029	1.034	0.919	0.919	0.927	0.927	1.008	1.011
		2	0.953	0.953	0.981	0.981	1.408	1.438	0.951	0.951	0.981	0.981	1.292	1.310
		3	0.982	0.982	1.042	1.043	2.084	2.197	0.980	0.980	1.035	1.035	1.901	1.980
	3	1	0.937	0.937	0.952	0.952	1.158	1.170	0.935	0.935	0.950	0.950	1.113	1.121
		2	0.965	0.965	1.010	1.010	1.684	1.744	0.963	0.963	1.010	1.010	1.540	1.580
		3	1.001	1.000	1.092	1.092	2.494	2.672	0.998	0.998	1.080	1.081	2.287	2.418
90°	1	1	0.539	0.538	0.542	0.542	0.543	0.564	0.533	0.533	0.535	0.534	0.542	0.542
		2	0.848	0.847	0.853	0.852	0.903	0.904	0.842	0.841	0.845	0.844	0.879	0.879
		3	0.914	0.913	0.921	0.921	1.095	1.104	0.910	0.911	0.916	0.916	1.054	1.059
	2	1	0.859	0.858	0.860	0.860	0.879	0.879	0.857	0.857	0.859	0.859	0.877	0.877
		2	0.917	0.917	0.922	0.922	1.024	1.027	0.917	0.917	0.922	0.922	0.997	0.999
		3	0.939	0.939	0.952	0.952	1.254	1.273	0.939	0.939	0.951	0.951	1.192	1.204
	3	1	0.900	0.900	0.904	0.904	0.959	0.962	0.899	0.899	0.902	0.902	0.957	0.959
		2	0.933	0.932	0.944	0.944	1.136	1.144	0.931	0.931	0.943	0.943	1.102	1.108
		3	0.950	0.950	0.977	0.977	1.430	1.462	0.949	0.948	0.976	0.976	1.354	1.377

In above analysis, only one edge is considered in the spherical shell. In Table 4, frequency parameters of a spherical shell with one or two free edges are presented. It’s observed that frequency parameters of present method agree well with the ones in [14] for all combinations of open angles $φ_{0}$ and $φ_{1}$ . It’s further observed that, for a fixed open angle $φ_{0}$ , frequency parameters do not monotonically increase or decrease as open angle $φ_{1}$ increases. The effect of open angle will be particularly investigated in the following.

Fig. 5Some axisymmetric mode shapes and frequency parameters Ω0m of the spherical shell with three different open angles

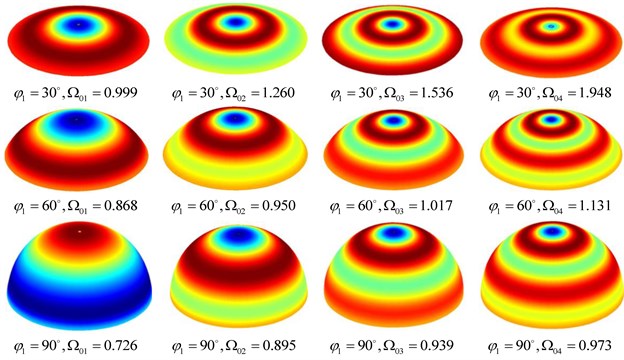
Table 4Comparison of frequency parameters of a spherical shell with one or two F boundary conditions (n= 2, m= 1, h/R= 0.01, v= 0.3)

$φ_{1}$	$φ_{0} =$ 0°		$φ_{0} =$ 30°		$φ_{0} =$ 45°		$φ_{0} =$ 60°		$φ_{0} =$ 75°
$φ_{1}$	Ref. [14]	Present	Ref. [14]	Present	Ref. [14]	Present	Ref. [14]	Present	Ref. [14]	Present
15°	0.23119	0.22999	–	–	–	–	–	–	–	–
30°	0.06195	0.06134	–	–	–	–	–	–	–	–
45°	0.02989	0.02950	0.02155	0.02123	–	–	–	–	–	–
60°	0.01884	0.01854	0.01656	0.01624	0.01290	0.01264	–	–	–	–
75°	0.01416	0.01391	0.01337	0.01310	0.01183	0.01153	0.00954	0.00932	–	–
90°	0.01231	0.01211	0.01200	0.01178	0.01121	0.01095	0.00983	0.00957	0.00829	0.00810
105°	0.01238	0.01219	0.01223	0.01204	0.01171	0.01148	0.01049	0.01022	0.00928	0.00902
120°	0.01470	0.01446	0.01461	0.01436	0.01402	0.01374	0.01214	0.01185	0.01049	0.01022
135°	0.02165	0.02117	0.02152	0.02103	0.01922	0.01874	0.01402	0.01374	0.01177	0.01148
150°	0.04395	0.04279	0.04124	0.04013	0.01992	0.02103	0.01461	0.01436	0.01223	0.01204
165°	0.16055	0.15746	0.04394	0.04278	0.02165	0.02116	0.01469	0.01445	0.01236	0.01216
180°	0.70101	0.70106	0.04395	0.04279	0.02165	0.02117	0.01470	0.01446	0.01238	0.01219

Based on above comparisons of frequency parameters of present method and literature, it can be concluded that present semi-analytic method can accurately analyze free vibrations of thin opened spherical shells.

3.2. Effects of boundary conditions

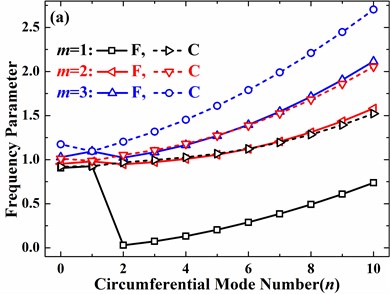
Fig. 6 presents effects of boundary conditions on the frequency parameters of a spherical shell with three different open angles. It’s observed that, as circumferential mode number is not less than 2, no matter what boundary conditions are, tendencies of frequency parameter versus circumferential mode number are identical, which means the increase of circumferential mode number leads to the increase of frequency parameter. However, as the circumferential mode number varies from 0 to 2, increasing circumferential mode number may lead to the increase or decrease of frequency parameter, which depends on the boundary conditions, open angle and meridional mode number. It’s also observed that, for a particular circumferential mode number, the frequency parameter of the mode with larger meridional mode number is always larger than the one with small meridional mode number. In addition, for $n =$ 0 and $n =$ 1, frequency parameters of $F$ are larger than the ones of $C$ , which is attributed to that the rigid modes are not considered for $F$ .

Fig. 6Effects of boundary conditions on frequency parameters of the spherical shell with different open angles (h/R= 0.01, v= 0.3, φ0= 0°): a) φ1= 45°, b) φ1= 90°, c) φ1= 135°

Effects of boundary conditions on frequency parameters of the spherical shell with different open angles (h/R= 0.01, v= 0.3, φ0= 0°): a) φ1= 45°, b) φ1= 90°, c) φ1= 135°

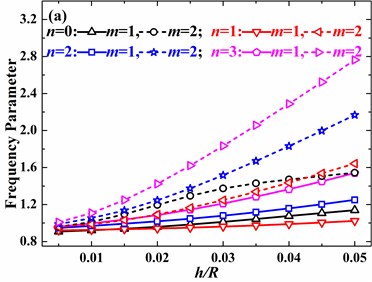
In Fig. 7, influences of elastic boundary conditions on free vibrations of a hemispherical shell are shown. Before analyzing the effects of elastic boundaries, it should be mentioned that only three curves in Fig. 7(a), which results from that the circumferential displacement is always 0 for $n =$ 0. In addition, every curve denotes that only one displacement is elastically restrained and the other three are fixed. It’s observed that effects of meridional and circumferential displacements are obviously greater than normal displacement and slope. However, with the increase of circumferential mode number, the effect of circumferential displacement becomes greater than meridonal displacement. Meanwhile, influences of normal displacement and slope become obvious as the circumferential mode number varies from 0 to 2. It’s further observed that the appropriate value of stiffness constant, which can significantly affect natural frequencies, is different for different circumferential mode numbers and directions of displacements, which is attributed to different values of stresses.

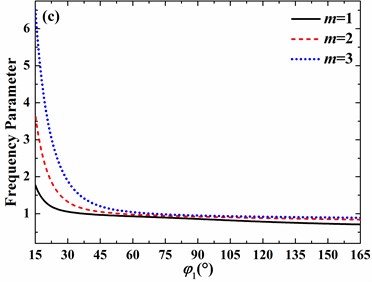
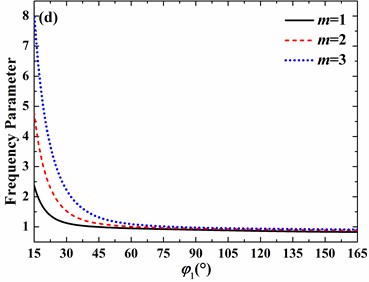
3.3. Effects of open angle

In Section 3.1, it is pointed out that the open angle has great influence on frequency parameters. In this section, influences of the open angle are discussed in detail. Fig. 8 and Fig. 9 show the effects of the open angle on frequency parameters of the free and clamped spherical shell, respectively. For free boundary conditions, on the one hand, the increase of the open angle can increase the frequency parameter as the open angle is small.

Fig. 7Effects of stiffness constants on frequency parameters of the hemispherical shell (m= 1, h/R= 0.01, v= 0.3, φ0= 0°): a) n= 0, b) n= 1, c) n= 2, c) n= 3

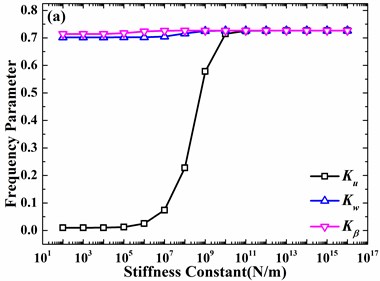
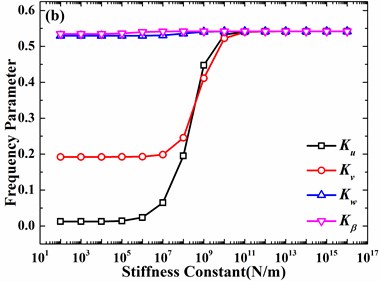
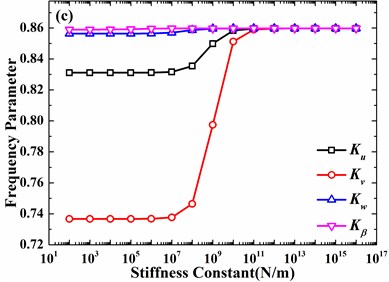
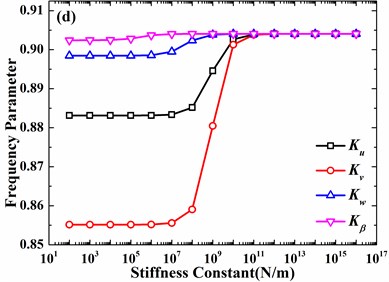
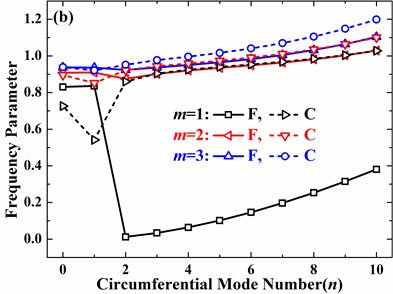
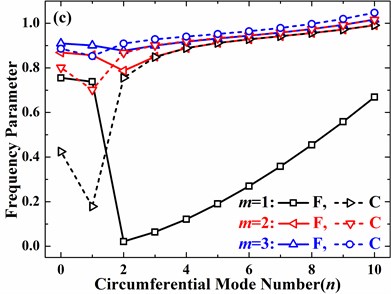
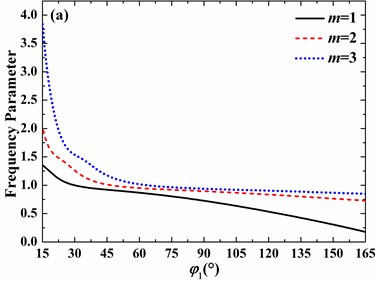
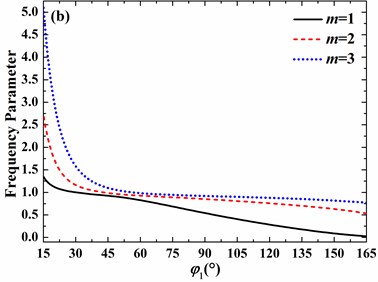
Fig. 8Effects of open angle on frequency parameters of the spherical shell with free boundary conditions (h/R= 0.01, v= 0.3, φ0= 0°): a) n= 0, b) n= 1, c) n= 2, d) n= 3

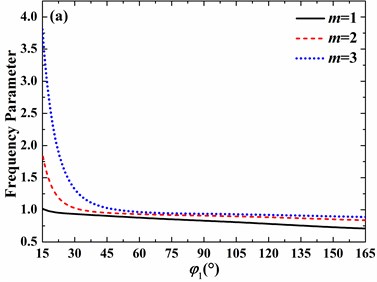
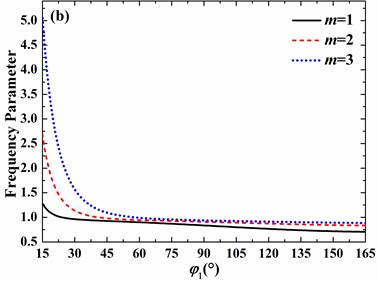
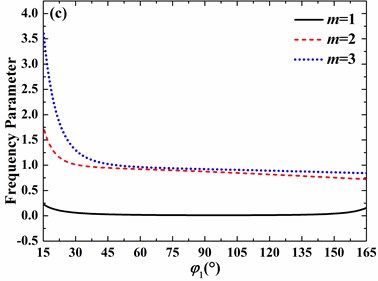
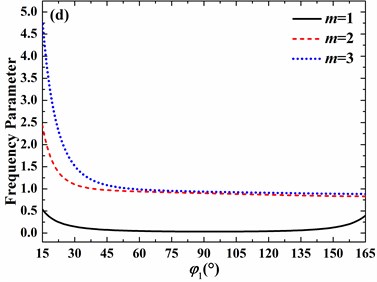
On the other hand, for no small open angle, the increase of open angle may lead to the increase or decrease of frequency parameter, which depends on the circumferential and meridional mode numbers. For clamped boundary conditions, with the increase of open angle, the frequency parameter always decreases as the circumferential mode number varies from 0 to 3 and meridional mode number changes from 1 to 3. In addition, as the circumferential mode number increases from 0 to 3, the decrease speed of frequency parameter becomes slower and slower as open angle is larger than 45°.

Fig. 9Effects of open angle on frequency parameters of the spherical shell with clamped boundary conditions (h/R= 0.01, v= 0.3, φ0= 0°): a) n= 0, b) n= 1, c) n= 2, d) n= 3

3.4. Effects of thickness to radius ratio

Effects of the ratio of thickness to radius on frequency parameters are presented in Fig. 10 and Fig. 11. Generally, frequency parameters are increased by the increase of the ratio of thickness to radius. However, effects of the ratio of thickness to radius on frequency parameters are dependent on the mode shape, open angle and boundary conditions. As the open angle increases, effects of the ratio of thickness to radius rapidly decrease, especially for $n =$ 0 and $n =$ 1, frequency parameters of which keep basically unchanged.

3.5. Effects of thickness discontinuity

In above study, the thickness of the shell is uniform, and non-uniform thickness can be also analyzed by present method. As a special case, a two-stepped hemi-spherical shell is employed and Fig. 12 shows the schematic diagram.

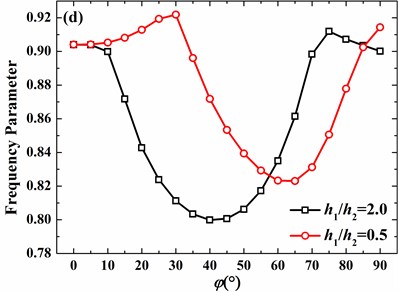
Influences of the location of thickness discontinuity on frequency parameters of the free and clamped hemispherical shell are presented in Fig. 13 and Fig. 14, respectively. It’s observed that tendencies of frequency parameters versus azimuth angle vary with circumferential mode numbers and boundary conditions.

Fig. 10Effects of the ratio of thickness to radius on frequency parameters of the spherical shell with free boundary conditions (v= 0.3, φ0= 0°): a) φ1= 45°, b) φ1= 90°, c) φ1= 135°

Effects of the ratio of thickness to radius on frequency parameters of the spherical shell with free boundary conditions (v= 0.3, φ0= 0°): a) φ1= 45°, b) φ1= 90°, c) φ1= 135°

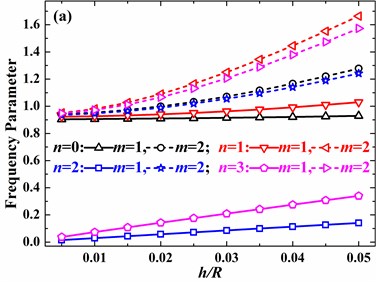
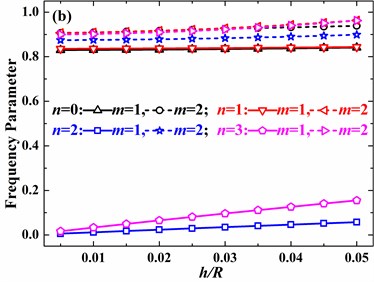
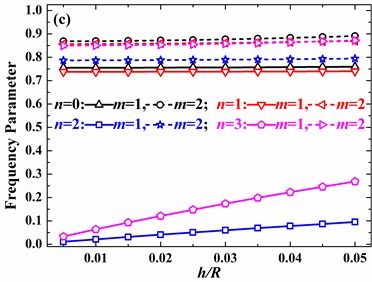
Fig. 11Effects of the ratio of thickness to radius on frequency parameters of the spherical shell with clamped boundary conditions (v= 0.3, φ0= 0°): a) φ1= 45°, b) φ1= 90°, c) φ1= 135°

Effects of the ratio of thickness to radius on frequency parameters of the spherical shell with clamped boundary conditions (v= 0.3, φ0= 0°): a) φ1= 45°, b) φ1= 90°, c) φ1= 135°

However, no matter what the modes and boundary conditions are, the tendencies of $h_{1} / h_{2} =$ 0.5 and $h_{1} / h_{2} =$ 2 are basically opposite. In the following analysis, effects of the discontinuity on frequency parameters of the hemispherical shell with $h_{1} / h_{2} =$ 2 are discussed in detail.

Fig. 12Schematic diagram of a two-stepped hemispherical shell

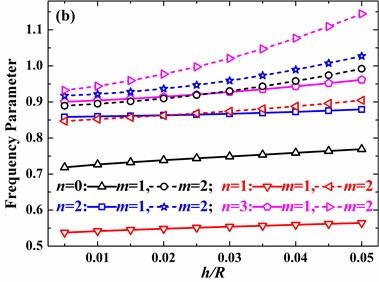
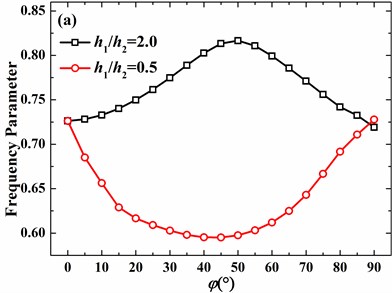
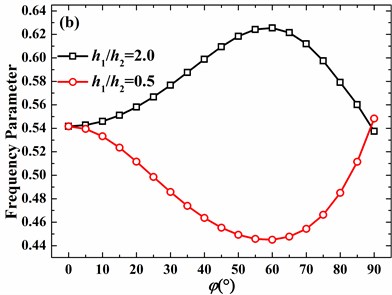
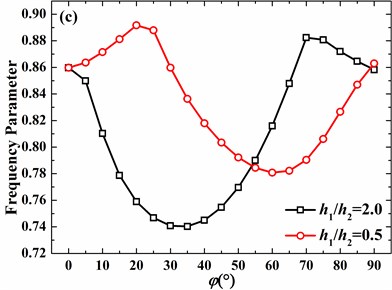
For the free hemispherical shell with $h_{1} / h_{2} =$ 2, the increase of azimuth angle of discontinuity may lead to the increase or decrease of frequency parameters as circumferential mode number is 0 and 1. Nevertheless, as circumferential mode number is 2 and 3, frequency parameter certainly decreases as the azimuth angle of discontinuity increases. It’s further observed that, as the azimuth angle of discontinuity is small, effects of azimuth angle of discontinuity are negligible for $n =$ 2 and $n =$ 3, which is different from those of $n =$ 0 and $n =$ 1.

Fig. 13Effects of thickness discontinuity on frequency parameters of the hemispherical shell with free boundary conditions (h1/R= 0.01, υ= 0.3, m= 1): a) n= 0, b) n= 1, c) n= 2, d) n= 3

Effects of thickness discontinuity on frequency parameters of the hemispherical shell with free boundary conditions (h1/R= 0.01, υ= 0.3, m= 1): a) n= 0, b) n= 1, c) n= 2, d) n= 3

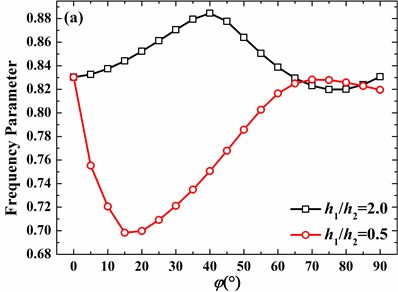
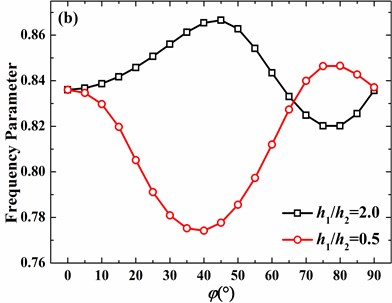
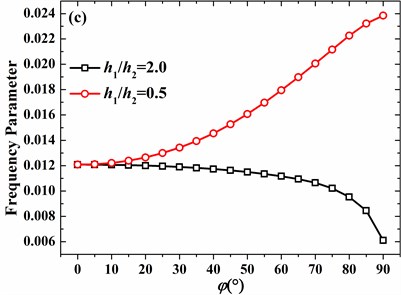
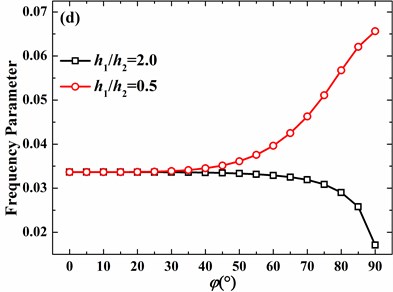
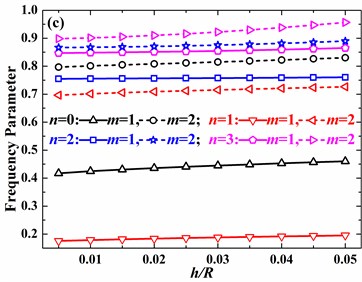
For the clamped hemispherical shell with $h_{1} / h_{2} =$ 2, the tendencies of $n =$ 0 and $n =$ 1 are simpler than those of $n =$ 2 and $n =$ 3. Frequency parameters firstly increase and then decrease as the azimuth angle of discontinuity increases for $n =$ 0 and $n =$ 1. For $n =$ 2 and $n =$ 3, as shown in Fig. 14(c) and (d), frequency parameters firstly decrease and then increase. Finally, as the azimuth angle closes to 90°, frequency parameters decrease again.

Fig. 14Effects of thickness discontinuity on frequency parameters of the hemispherical shell with clamped boundary conditions (h1/R= 0.01, v= 0.3, m= 1): a) n= 0, b) n= 1, c) n= 2, d) n= 3

Effects of thickness discontinuity on frequency parameters of the hemispherical shell with clamped boundary conditions (h1/R= 0.01, v= 0.3, m= 1): a) n= 0, b) n= 1, c) n= 2, d) n= 3

4. Conclusions

In present paper, a semi-analytical method was proposed to analyze both axisymmetric and asymmetric modes of spherical shells with elastic boundary conditions and discontinuity in thickness. To establish the governing equation, the spherical shell is firstly divided into many narrow strips, which are approximately treated as conical shells. Based on Flügge thin shell theory and power series method, displacements and forces at the cross-section of strips are expressed in terms of eight unknown coefficients. Lastly, continuity conditions of adjacent strips and boundary conditions are assembled to the final governing equation. By comparing frequency parameters of present method with those in literature, high accuracy and wide application of present method are verified. As circumferential mode number is small, frequency parameter may increase or decrease as circumferential mode number increases. On the other hand, the increase of circumferential mode number certainly results in the increase of frequency parameters for no small circumferential mode number. The effects of stiffness constants of elastic boundaries illustrate that meridional and circumferential displacements have the greatest effects on frequency parameters, and the effects of normal displacement and slope becomes obvious as circumferential mode number varies from 0 to 3. For $φ_{0} =$ 0°, increasing the open angle $φ_{1}$ can significantly reduce the frequency parameters as the open angle is small. However, as the open angle is greater than 125°, the increase of open angle may lead to the increase or decrease of frequency parameters, which strongly depends on the boundary conditions and circumferential mode number. The frequency parameters increase as the ratio of thickness to radius increases. Nevertheless, for $n =$ 0 and $n =$ 1, the effect of the ratio thickness to radius is negligible as open angle $φ_{1}$ is between 90° and 135°. The location of thickness discontinuity is of great influence on frequency parameters, and the influence strongly depends on the boundary conditions, circumferential mode number and thickness ratio $h_{1} / h_{2}$ .

The proposed method can accurately and efficiently analyze free vibrations of spherical shells. In the subsequent work, spherical shells coupled with other revolution shells, e.g. cylindrical and conical shells, will be investigated since continuity conditions between spherical shells and others can be accurately satisfied without difficulty. In addition, it should be mentioned that the continuity conditions may be the bottleneck to analyze vibrations of coupled spherical-cylindrical or spherical-conical shells because there are many papers studying coupled cylindrical-cylindrical, conical-conical and cylindrical-conical shells whereas the literature about couple shells including spherical shells is rare.

References

Kalnins A., Naghdi P. Axisymmetric vibrations of shallow elastic spherical shell. Journal of the Acoustical Society of America, Vol. 32, Issue 3, 1960, p. 342-347.

Publisher
Baker W. E. Axisymmetric modes of vibration of thin spherical shell. Journal of the Acoustical Society of America, Vol. 33, Issue 12, 1961, p. 1749-1758.

Publisher
Hoppmann II W. H., Baker W. E. Extensional vibrations of elastic orthotropic spherical shells. Journal of Applied Mechanics, Vol. 28, Issue 2, 1961, p. 229-237.

Publisher
Hoppmann II W. H. Frequencies of vibration of shallow spherical shells. Journal of Applied Mechanics, Vol. 28, Issue 2, 1961, p. 305-307.

Publisher
Kalnins A. On vibration of shallow spherical shells. Journal of the Acoustical Society of America, Vol. 33, Issue 8, 1961, p. 1102-1107.

Publisher
Naghdi P. M., Kalnins A. On vibrations of elastic spherical shells. Journal of Applied Mechanics, Vol. 29, Issue 1, 1962, p. 65-72.

Publisher
Kalnins A. Effect of bending on vibrations of spherical shells. Journal of the Acoustical Society of America, Vol. 36, Issue 1, 1964, p. 74-81.

Publisher
Prasad C. On vibration of spherical shells. Journal of the Acoustical Society of America, Vol. 36, Issue 3, 1964, p. 489-494.

Publisher
Wilkinson J. P., Kalnins A. On nonsymmetric dynamic problems of elastic spherical shells. Journal of Applied Mechanics, Vol. 32, Issue 3, 1965, p. 525-532.

Publisher
Ramakrishnan C. V., Shah A. H. Vibration of an aelotropic spherical shell. Journal of the Acoustical Society of America, Vol. 47, Issue 5, 1970, p. 1366-1374.

Publisher
Martynenko V. S., Shapakova S. G. Asymmetric vibrations of spherical shells. International Applied Mechanics, Vol. 9, Issue 10, 1973, p. 1059-1063.

Publisher
Chakrabarti R. Forced vibrations of non-homogeneous isotropic elastic spherical shell. Pure and Applied Geophysics, Vol. 112, Issue 1, 1974, p. 52-57.

Publisher
Kunieda H. Flexural axisymmetric free vibrations of a spherical dome: exact results and approximate solutions. Journal of Sound and Vibration, Vol. 92, Issue 1, 1984, p. 1-10.

Publisher
Niordson F. I. Free vibration of thin elastic spherical shells. International Journal of Solids and Structures, Vol. 20, Issue 7, 1984, p. 667-687.

Publisher
Niordson F. I. The spectrum of free vibrations of a thin elastic spherical shell. International Journal of Solids and Structures, Vol. 24, Issue 9, 1988, p. 947-961.

Publisher
Chen W. Q., Ding H. J. Free vibration of multi-layered spherically isotropic hollow spheres. International Journal of Mechanical Sciences, Vol. 43, 2001, p. 667-680.

Publisher
Lee J. Free vibration analysis of spherical caps by the pseudospectral method. Journal of Mechanical Science and Technology, Vol. 23, 2009, p. 221-228.

Publisher
Lee J. Free vibration analysis of a hermetic capsule by pseudospectral method. Journal of Mechanical Sciences and Technology, Vol. 26, Issue 4, 2012, p. 1011-1015.

Publisher
Su Z., Jin G. Y., Shi S. X., Ye T. G. A unified accurate solution for vibration analysis of arbitrary functionally graded spherical shell segments with general end restrains. Composite Structures, Vol. 111, 2014, p. 271-284.

Publisher
Chernobryvko M. V., Avramov K. V., Romanenko V. N., Batutina T. J., Tonkonogenko A. M. Free linear vibrations of thin axisymmetric parabolic shells. Meccanica, Vol. 49, Issue 12, 2014, p. 2839-2845.

Publisher
Kang J. H. Free vibration analysis of shallow spherical dome by three-dimensional Ritz method. Journal of Vibration and Control, Vol. 22, Issue 11, 2016, p. 2731-2744.

Publisher
Zarghamee M. S. Robinson A. R. A numerical method for analysis of free vibration of spherical shells. AIAA Journal, Vol. 5, Issue 7, 1976, p. 1256-1261.

Publisher
De Souza V. C. M., Croll J. G. A. An energy analysis of the free vibrations of isotropic spherical shell. Journal of Sound and Vibration, Vol. 73, Issue 3, 1980, p. 379-404.

Publisher
Singh A. V., Mirza S. Asymmetric modes and associated eigenvalues spherical shells. Journal of Pressure Vessel Technology, Vol. 107, Issue 1, 1985, p. 77-82.

Publisher
Singh A. V. On vibrations of shells of revolution using Bezier polynomials. Journal of Pressure Vessel Technology, Vol. 113, Issue 4, 1991, p. 579-584.

Publisher
Fan S. C., Luah M. H. Free vibration analysis of arbitrary thin shell structures by using spline finite element. Journal of Sound and Vibration, Vol. 179, Issue 5, 1995, p. 763-776.

Publisher
Gautham B. P., Ganesan N. Free vibration characteristics of isotropic and laminated orthotropic spherical caps. Journal of Sound and Vibration, Vol. 204, Issue 1, 1997, p. 17-40.

Publisher
Wu Y. C., Heyliger P. Free vibration of layered piezoelectric spherical caps. Journal of Sound and Vibration, Vol. 245, Issue 3, 2001, p. 527-544.

Publisher
Sai Ram K. S., Sreedhar Babu T. Free vibration of composite spherical shell cap with and without a cutout. Computers and Structures, Vol. 80, Issue 23, 2002, p. 1749-1756.

Publisher
Artioli E., Viola E. Free vibration analysis of spherical caps using a G.D.Q. numerical method. Journal of Pressure Vessel Technology, Vol. 128, Issue 3, 2006, p. 370-378.

Publisher
Tornabene F., Viola E. Vibration analysis of spherical shell structures element using the GDQ method. Computers and Mathematics with Applications, Vol. 53, Issue 10, 2007, p. 1538-1560.

Publisher
Simmonds J. G., Hosseinbor A. P. The free and forced vibrations of a closed elastic spherical shell fixed to an equatorial beam-part I: the governing equations and special solutions. Journal of Applied Mechanics, Vol. 77, Issue 2, 2010, p. 021017.

Publisher
Simmonds J. G., Hosseinbor A. P. The free and forced vibrations of a closed elastic spherical shell fixed to an equatorial beam-part II: perturbation approximations. Journal of Applied Mechanics, Vol. 77, Issue 2, 2010, p. 021018.

Publisher
Qu Y. G., Long X. H., Yuan G. Q., Meng G. A unified formulation for vibration analysis of functionally graded shells of revolution with arbitrary boundary conditions. Composites Part B: Engineering, Vol. 50, 2013, p. 381-402.

Publisher
Choi M. S., Kondou T., Choi H. J. Free vibration analysis of axisymmetric shells with various shapes using Sylvester-transfer stiffness coefficient method. Journal of Mechanical Sciences and Technology, Vol. 29, Issue 7, 2015, p. 2755-2766.

Publisher
Naghsh A., Saadatpour M. M., Azhari M. Free vibration analysis of stringer stiffened general shells of revolution using a meridional finite strip method. Thin-Walled Structures, Vol. 94, 2015, p. 651-662.

Publisher
Cui X. Y., Wang G., Li G. Y. A nodal integration axisymmetric thin shell model using linear interpolation. Applied Mathematical Modelling, Vol. 40, 2016, p. 2720-2742.

Publisher
Brown D., Brown C. T. Investigation of vibrations of piezoelectric spherical shells with axisymmetric holes. Proceedings of Meetings on Acoustics, Vol. 19, 2013, p. 030065.

Publisher
Leissa A. W. Vibrations of Shells. Acoustical Institute of Physics, New York, 1993.

Search CrossRef
Xie K., Chen M. X., Deng N. Q., Jia W. C. Free and forced vibration of submerged ring-stiffened conical shells with arbitrary boundary conditions. Thin-Walled Structures, Vol. 96, 2015, p. 240-255.

Publisher
Tong L. Y. Free vibration of orthotropic conical shells. International Journal of Engineering Science, Vol. 31, Issue 5, 1993, p. 719-733.

Publisher

Cited by

Design of a simplified cranial substitute with a modal behavior close to that of a human skull

(2024)

Theoretical modeling and vibration analysis of composite laminated wing-box structures of hydrogen-electric aircraft under hygrothermal environment

Xu-Yuan Song | Wen-Rui Zhao | Jian Zang | Zhen Zhang | Ye-Wei Zhang

(2024)

Simple first-order shear deformation theory for free vibration of FGP-GPLRC spherical shell segments

Van-Loi Nguyen | Suchart Limkatanyu | Huu-Tai Thai | Jaroon Rungamornrat

(2024)

Geometrically nonlinear vibration analysis of eccentrically stiffened porous functionally graded annular spherical shell segments

Seyed Sajad Mirjavadi | Masoud Forsat | Mohammad Reza Barati | A. M. S Hamouda

(2022)

A formulation for turbulent-flow-induced vibration of elastic plates with general boundary conditions

Xiaoji Song | Guoyong Jin | Tiangui Ye | Saifeng Zhong

(2021)

FEM exploration of the potential of silica diatom frustules for vibrational MEMS applications

Bakhodur Abdusatorov | Alexey I. Salimon | Yekaterina D. Bedoshvili | Yelena V. Likhoshway | Alexander M. Korsunsky

(2020)

Underlying Subwavelength Aperture Architecture Drives the Optical Properties of Microcavity Surface Plasmon Resonance Sensors

Dragos Amarie | Nazanin Mosavian | Elijah L. Waters | Dwayne G. Stupack

(2020)

About this article

Received

11 May 2016

Accepted

19 September 2016

Published

30 June 2017

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/jve.2016.17154

Keywords

opened spherical shells

semi-analytical method

elastic boundary conditions

stepwise thickness

free vibration analysis

Acknowledgements

The present research obtains great financial support from the National Natural Science Foundation of China (Grant No. 51179071).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2019 11 28

Free vibration analysis of simply supported rectangular plates

Ganesh Naik Guguloth, Baij Nath Singh, Vinayak Ranjan

Research article

2017 09 30

Shooting method for free vibration of FGM Reissner-Mindlin circular plates resting on elastic foundation in thermal environments

Qing-Lu Li, Wei-Di Luan, Zuo-Quan Zhu

Research article

2017 08 15

Free vibration analysis of moderately thick isotropic homogeneous open cylindrical shells using improved Fourier series method

Fazl e Ahad, Dongyan Shi, Zarnab Hina, Rehman Anees Ur

Research article

2017 02 15

Computational approaches to vibration analysis of shells under different boundary conditions – a literature review

Fazl e Ahad, Dongyan Shi, Zarnab Hina

K. Xie, M. Chen, and Z. Li, “A semi-analytical method for vibration analysis of thin spherical shells with elastic boundary conditions,” Journal of Vibroengineering, Vol. 19, No. 4, pp. 2312–2330, Jun. 2017, https://doi.org/10.21595/jve.2016.17154

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2016.17154
UR  - https://doi.org/10.21595/jve.2016.17154
TI  - A semi-analytical method for vibration analysis of thin spherical shells with elastic boundary conditions
T2  - Journal of Vibroengineering
AU  - Chen, Meixia
AU  - Xie, Kun
AU  - Li, Zuhui
PY  - 2017
DA  - 2017/06/30
PB  - JVE International Ltd.
SP  - 2312-2330
IS  - 4
VL  - 19
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Chen_2017,
	doi = {10.21595/jve.2016.17154},
	url = {https://doi.org/10.21595/jve.2016.17154},
	year = 2017,
	month = {jun},
	publisher = {{JVE} International Ltd.},
	volume = {19},
	number = {4},
	pages = {2312--2330},
	author = {Meixia Chen and Kun Xie and Zuhui Li},
	title = {A semi-analytical method for vibration analysis of thin spherical shells with elastic boundary conditions},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]M. Chen, K. Xie, and Z. Li, “A semi-analytical method for vibration analysis of thin spherical shells with elastic boundary conditions,” Journal of Vibroengineering, vol. 19, no. 4, pp. 2312–2330, Jun. 2017, doi: 10.21595/jve.2016.17154.

Copy IEEE

Copied to clipboard!

Chen, Meixia, Kun Xie, and Zuhui Li. “A Semi-Analytical Method for Vibration Analysis of Thin Spherical Shells with Elastic Boundary Conditions.” Journal of Vibroengineering 19, no. 4 (June 30, 2017): 2312–30. https://doi.org/10.21595/jve.2016.17154.

Copy Chicago

Copied to clipboard!

A semi-analytical method for vibration analysis of thin spherical shells with elastic boundary conditions

Abstract

1. Introduction

2. Theoretical formulations

2.1. Basic concept of the semi-analytical method

2.2. Equations of motion of conical shells

2.3. Boundary and continuity conditions

2.4. Final governing equation

3. Numerical results and discussion

3.1. Convergence and validity

3.2. Effects of boundary conditions

3.3. Effects of open angle

3.4. Effects of thickness to radius ratio

3.5. Effects of thickness discontinuity

4. Conclusions

References

Cited by

About this article

Related Articles