Assessment and comparison of likely density distributions in the cases of thickness measurement of skin tumours by ultrasound examination and histological analysis

1. Introduction

The storage of medical information and its statistical analysis are being carried out since the middle of ages. The first known statistical journal of medicine was published in London, in 1662 [1]. In 1863, F. Nightingale, the pioneer of nowadays nursing, raised the problem about the lack of medical statistics records and non-systematic storage in hospitals, as a consequence of treatment effectiveness and costs limited analysis. In 1977 the US Congress published a study “Medical information systems practitioner’s consequences” [2]. It states, that medical information systems can be a useful tool for training, also to help medicine and health care specialists leading to higher quality of facilities and optimization of health care institution activity. The authors of study have confirmed that medical information system will be a useful tool for researches and health governing institutions. Since 2000, the active global implementation of regional and national electronic health records systems started. The aim of these systems is to save all important patients medical records. Lithuanian health sector also applies information technologies, creating a national electronic health services and information system for cooperation infrastructure, also subsystem for national medical images archiving and exchange. Health care institutions implement and improve information systems of hospitals, systems for radiological images preview and archiving, information systems of laboratories [3]. Information system of the health care keeps a structured information about the patient, such as diagnosis, demographic patient data, vital functions, test results and etc. These data analysis and mining are very important for all patients. The smart analysis of patient records helps to solve tasks as a faster diagnostic, choosing of optimal treatment, prediction of treatment period and results, to identify the risk of complications, resources optimization of the health care institutions. Last decade, data mining research in biomedicine is highly considered [4, 5]. Data mining methods and algorithms can be useful if researches clearly understand scopes, types of the data and peculiarities. The most common tasks mentioned in literature are classification, clustering, prediction, association, visualization, identification of deviations and analysis of internal links. For these data mining tasks, we need to choose a suitable algorithm. Choosing of method or an optimal algorithm depends on aims of task analysis and data characteristics. Over the last decade, there are found enough methods of data mining application in medicine. In diagnosis there are widely applied neural networks, decision trees, decision rules [6], methods for search of associative rules (for costs analysis) [7], prediction of patient health and treatment probability, also very popular to use combinations of prediction algorithms [5]. In 2014, N. Esfandiari et al. [4], carried out a literature review, there are described applications of data mining in medicine based on analysis of the structured data. There are stated that classification (neural networks, decision trees, decision rules, support vector model), clustering (k-means, hierarchical clustering) and associative search (a priori associative rules search) models are the most popular in medicine. Lalayants et al. [8] have said that the solution of successful medical data mining is to identify the right activity of health care institution or to find the clinical problem. Data mining methods are usually used in biomedical data analysis and visualization tasks in order to facilitate decision-making [9]. If the data mining process would be enough simple, the management of information problems would be already solved long time ago (R. Bellazzi, B. Zupan [5]). Practical data mining application in medicine has some obvious barriers as technological problems, trans-disciplinary communication, ethics and patient data security [7, 9, 10]. Medical research leads to a lot of data characterizing the condition of patient. All these data are dynamically changing and depend on patient illness, patient biological condition, environment, the quality of life, related diseases and other actually reasons, those can be described as a random factor. The change of medical statistics observations is described by primary statistics analysis. The results lead to further instructions of medical research and affect hardly choosing and application of the appropriate statistical method. The reliability of above mentioned methods usually depends on the assumption of data distribution – normal, binomial and etc. Therefore, at first, it is necessary to check the appropriate assumption. This paper will present a simple, effective method of nonparametric statistics and some hypothesis criteria about the variable distribution and identity checking of two distributions. These hypotheses are called goodness of fit test hypothesis. The purpose of research is to determine the connection between thicknesses of the skin tumours measured by non-invasive ultrasonic technique and after a surgical intervention measured histologically by optical microscope. Also, to compare the compatibility of likely density of histological thicknesses distribution of the skin tumours and Normal distribution density this method is effective for structured big data matrix and simple to use. There is no problem to check the sample which is distributed by well-known theoretical distribution, because these cases are already examined both theoretically as well as empirically. The biggest challenge is to check the identity between two samples. As a solution the most commonly used techniques relies on differences of density distribution. Even in nowadays data analysis there are a lot of evaluation methods of density distribution, but in practice it is not easy to find the effective evaluation procedure if the data distribution is multimodal and the volume of sample is small. Kernel smoothing is the most frequently used nonparametric estimation method (see Jones, et al., 1996 [11], Marron and Wand, 1992 [12]; Silverman, 1986 [13]). Thus far, there is no generally accepted method for kernel estimation, which outperforms the other in all cases. Although many adaptive selection procedures have been proposed (Bashtannyk and Hyndman, 1998 [14]; Jones, 1992 [15]; Zhang et al., 2004 [16]), their efficiency has not been well established yet, especially for samples of a moderate size. On the basis of Lithuanian cancer register data, Lithuania established more than 250 melanomas cases every year. Even Lithuania is not included in the list of biggest melanomas risk country, but the statistics shows that the number of melanomas cases in Lithuania is increasing every year. The main reason is too late diagnosis. Usually melanoma is diagnosed in 2-4 stages. The mortality of melanoma in Lithuania is bigger than in other Europe countries [17, 18]. Melanoma is a rapidly growing and spreading malignant tumor, rarely amenable to treat through the spread of time. In the absence of effective treatment of metastatic melanoma, a key factor of survival of melanoma is early diagnosis and urgent surgical removal of the primary tumor. The earlier diagnosis of melanoma can be prevented by regularly checking of nevus and disposal nevus, those can be malignant. Surgical removal of melanoma having thickness of 1 mm increase the probability of survival, for 10 the years survival rate is 90-97 percent [19, 20].

The paper consists of 6 sections. Section 2 reviews the kernel density estimator and kernel functions; Section 3 proves optimal selection of smoothing parameter; Section 4 describes the simulation experiment and contains the simulation results; Section 5 shows the analysis in an empirical context using the retrospective observations of thicknesses of the skin tumour for goodness of fit tests; the concluding remarks are presented in Section 6.

2. Kernel density estimator

A d-dimensional random vector $X\in R^d$ satisfies a mixture model if its distribution density function $f\left(x\right)$ is given by the equality:

The parameter $q$ is the number of components in the mixture. The component weights $p_k$ are called a priori probabilities and satisfy the conditions:

Function $f_k\left(x\right)$ is the distribution density function of the $k$th component and $\theta$ is the vector of parameters of mixture model Eq. (1). Suppose a simple sample $\mathbf{X}=\left(X\left(1\right),\dots ,X\left(n\right)\right)$ of size n from $\mathbf{X}$ is given. The estimation of the distribution density of an observed random vector is one of the main statistical tasks.

A histogram is one of the simplest and the oldest density estimators. This graphical representation was first introduced by Karl Pearson in 1891 (Scott, 1992 [21]). For the approximation of density $f\left(x\right)$, the number of observations $X\left(t\right)$ falling within the range of $\mathrm{\Omega }$ is calculated and divided by n and the volume of area $\mathrm{\Omega }$. The histogram produced is a step function and the derivative either equals zero or is not defined (when at the cut off point for two bins). This is a big problem if we are trying to maximize a likelihood function that is defined in terms of the densities of the distributions.

It is remarkable that the histogram stood as the only nonparametric density estimator until the 1950’s, when substantial and simultaneous progress was made in density estimation and in spectral density estimation. In 1951, in a little-known paper, Fix and Hodges [22] introduced the basic algorithm of nonparametric density estimation; an unpublished technical report was published formally as a review by Silverman and Jones in 1989 [23]. They addressed the problem of statistical discrimination when the parametric form of the sampling density was not known. During the following decade, several general algorithms and alternative theoretical modes of analysis were introduced by Rosenblatt in 1956 [24], Parzen in 1962 [25], and Cencov in 1962 [26]. Then followed the second wave of important and primarily theoretical papers by Watson and Leadbetter in 1963 [27], Loftsgaarden and Quesenberry in 1965 [28], Schwartz in 1967 [29], Epanechnikov in 1969 [30], Tarter and Kronmal in 1970 [31] and Kimeldorf and Wahba in 1971 [32]. The natural multivariate generalization was introduced by Cacoullos in 1966 [33]. Finally, in the 1970’s the first papers focusing on the practical application of these methods were published by Scott et al. in 1978 [34] and Silverman in 1978 [35]. These and later multivariate applications awaited the computing revolution.

The basic kernel estimator $\widehat{f}\left(x\right)$ with a kernel function $K$ and a fixed (global) bandwidth h for multivariate data $X\in {\mathbf{R}}^d$ may be written compactly as:

The kernel function $K\left(u\right)$ should satisfy the condition:

Usually, but not always, $K\left(u\right)$ will be a symmetric probability density function $K\left(u\right)=K(-u)$ for all values of u (see Silverman, 1986 [13]).

At first, the data is usually prescaled in order to avoid large differences in data spread. A natural approach (see Fukunaga, 1972 [36]) is first to standardize the data by a linear transformation yielding data with zero mean and unit variance. As a result, Eq. (3) is applied to the standardized data. Let $Z$ denote the sphered values of random $X$:

where $\stackrel{-}{X}$ is the empirical mean, and $S\in R^{d\times d}$ is the empirical covariance matrix. Applying the kernel density estimator to the standardized data $Z=\left(Z\left(1\right),\dots ,Z\left(n\right)\right)$ yields the following estimator of density function $f\left(x\right)$:

The comparative analysis of estimation accuracy was made for four different types of kernels. The first three kernels are classical, whereas the last one is new.

The Gaussian kernel is consistent with the distribution of normal $\phi \left(x\right)$ (see Gasser et al., 1985 [37], Marron and Nolan, 1988 [38]) selection:

The Epanechnikov kernel is the second order polynomial, corrected to satisfy the properties of the density function (see Epanechnikov, 1969 [30], Sacks and Ylvisaker, 1981 [39]):

where $V_d={\pi }^{d/2}/\mathrm{\Gamma }(d/2+1)$ is the volume of the d-dimensional unit sphere, and $\mathrm{\Gamma }\left(u\right)={\int }_0^{\infty }{y}^{u-i}{e}^{-y}dy.$

The Triweight kernel proposed by Tapia and Thompson in 1978 [40] has better smoothness properties and finite support. It was investigated in detail by Hall in 1985 [41]:

The new kernel $K_{New}$ has lighter tails than Gaussian distribution density and was introduced by the authors of this article:

This kernel function depends on parameter $\alpha$. In simulations, the chosen values of the parameter were 0.25, 0.5, and 0.75. The first two values produce worse accuracy results in comparison with the value of 0.75. Therefore, only the results obtained for $\alpha =$ 0.75 are reported here.

3. Optimal bandwidth selection

There are three parameters in kernel density estimator: the sample size $n$, the kernel function $K\left(\bullet \right)$ and the bandwidth $h$. Quite typically we cannot do anything about the sample size and we have to make the best out of the situation by choosing an appropriate kernel and a suitable bandwidth. It is well known that the bandwidth selection is the most crucial step in order to obtain a good estimate (see Wand and Jones, 1995 [42]). Unfortunately, bandwidth selection is the most difficult problem in kernel density estimation and a definite and unique solution to this problem does not exist.

It is rather surprising that the most effective bandwidth selection method is a visual assessment by the researcher. The researcher visually compares different density estimates, based upon a variety of bandwidths and then chooses the bandwidth that corresponds to the subjectively optimal estimate. The unfortunate part is that such bandwidths are non-unique; this method will yield different bandwidths when performed by different researchers. This method can also be very time consuming.

The approach based on mathematical analysis is to quantify the discrepancy between the estimate and the target density by evaluated error criterion. The optimal bandwidth will then be the bandwidth value that minimizes the error measured by the error criterion. Such a method is objective and can be time-efficient as computers can solve it numerically.

A global measure of precision is the asymptotic mean integrated squared error (AMISE):

where ${\nabla }^{\nu }f\left(x\right)=\sum _{k=1}^d{\partial }^{\nu }/\partial x_k^{\nu }f\left(x\right)$ and $R\left(g\right)={\int }_{-\infty }^{\infty }g{\left(u\right)}^{2}du$ is the roughness of a function. The order of a kernel, $v\text{,}$ is defined as the order of the first non-zero moment ${\kappa }_j\left(K\right)={\int }_{-\infty }^{\infty }{u}^{j}K\left(u\right)du.$ For example, if ${\kappa }_1\left(K\right)=0$ and ${\kappa }_2\left(K\right)>0$ then $K$ is a second-order kernel and $v=$ 2. If ${\kappa }_1\left(K\right)={\kappa }_2\left(K\right)={\kappa }_3\left(K\right)=0$ but ${\kappa }_4\left(K\right)>0$ then $K$ is a fourth-order kernel and $v=$ 4.The order of a symmetric kernel is always even. Symmetric non-negative kernels are second-order kernels. A kernel is higher-order kernel if $v>$ 2. These kernels will have negative parts and are not probability densities.

The optimal bandwidth is:

The optimal bandwidth depends on the unknown quantity $R\left({\nabla }^{\left(\nu \right)}f\right)$. For a rule-of-thumb bandwidth, Silverman proposed that it is possible to try the bandwidth computed by replacing $f$ in the optimal formula by $g_0$ where $g_0$ is a reference density – a plausible candidate for $f$, and $\widehat{\sigma }$ is the sample standard deviation (see Bruce E. Hansen, 2009 [43]). The standard choice is a multivariate normal density. The idea is that if the true density is normal, then the computed bandwidth will be optimal. If the true density is reasonably close to the normal, then the bandwidth will be close to optimal. Calculation of that is proceeded according to:

where the double factorial means $\left(2s+1\right)!!=\left(2s+1\right)\left(2s–1\right)\dots 5\bullet 3\bullet 1\text{.}$ Making this substitution, we obtain:

where:

and this assumed that variance is equal to 1. Rescaling the bandwidths by the standard deviation of each variable, we obtain the rule-of-thumb bandwidth for the $i$th variable is:

Table 1 provides the normal reference rule-of-thumb constants ($C_v\left(K,d\right)$ in (Eq. (15)) for the second-order d-variate kernel density estimator. We point out several striking features. First, in the common setting of a second order kernel ($v=$ 2) the rule-of-thumb constants are decreasing as d increases. Scott (1992 [21]) notes that these reach a minimum when $d=$ 11. The $v=$ 2 case is the only one he considers. When $v>$ 2, it is possible to show that the rule-of-thumb constants are increasing in the dimensionality of the problem. The basic idea behind this is given that higher-order kernels reduce bias; larger bandwidths are needed to minimize AMISE. However, note that the increase is not uniform over $v$.

4. The analysis of estimation accuracy

A comprehensive simulation study was conducted with the aim to compare the kernel functions described before. The main attention is paid to the case where the density of independent d-dimensional observations is GMM:

where $\theta =\left(p_i,M_i,R_i,i=\mathrm{1,2},\dots ,q\right)$. Univariate, bi-variate, and quinta-variate GMMs, from a suggested collection was used in comparative analysis as the benchmark densities:

1) Gaussian

$p_1=$ 1, $M_1=\left(0,\dots ,0\right)$, $R_1=I=diag\left(\left[1,\dots ,1\right]\right)$

2) skewed unimodal

$p_1=$ 1/5, $M_1=\left(0,\dots ,0\right)$, $R_1=I=diag\left(\left[1,\dots ,1\right]\right)$

$p_2=$1/5, $M_2=\left(1/\mathrm{2,0},\dots ,0\right)$, $R_2=diag\left(\left[{\left(2/3\right)}^2,\dots ,{\left(2/3\right)}^2\right]\right)$

$p_3=$ 3/5, $M_3=\left(13/\mathrm{12,0},\dots ,0\right)$, $R_3=diag\left(\left[{\left(5/9\right)}^2,\dots ,{\left(5/9\right)}^2\right]\right)$

3) strongly skewed

$p_n=$ 1/8, $M_n=\left(3\left({\left(2/3\right)}^n-1\right),0,\dots ,0\right)$, $R_n=diag\left(\left[{\left(2/3\right)}^{2n},\dots ,{\left(2/3\right)}^{2n}\right]\right)$, $n=$ 0, …, 7

4) kurtotic unimodal

$p_1=$ 2/3, $M_1=\left(0,\dots ,0\right)$, $R_1=I=diag\left(\left[1,\dots ,1\right]\right)$

$p_2=$ 1/3, $M_2=\left(0,\dots ,0\right)$, $R_2=diag\left(\left[{\left(1/10\right)}^2,\dots ,{\left(1/10\right)}^2\right]\right)$

5) outlier

$p_1=$ 1/10, $M_1=\left(0,\dots ,0\right)$, $R_1=I=diag\left(\left[1,\dots ,1\right]\right)$

$p_2=$ 9/10, $M_2=\left(0,\dots ,0\right)$, $R_2=diag\left(\left[{\left(1/10\right)}^2,\dots ,{\left(1/10\right)}^2\right]\right)$

6) bimodal

$p_1=$ 1/2, $M_1=\left(-\mathrm{1,0},\dots ,0\right)$, $R_1=diag\left(\left[{\left(2/3\right)}^2,\dots ,{\left(2/3\right)}^2\right]\right)$

$p_2=$ 1/2, $M_2=\left(\mathrm{1,0},\dots ,0\right)$, $R_2=diag\left(\left[{\left(2/3\right)}^2,\dots ,{\left(2/3\right)}^2\right]\right)$

7) separated bimodal

$p_1=$ 1/2, $M_1=\left(-3/\mathrm{2,0},\dots ,0\right)$, $R_1=diag\left(\left[{\left(1/2\right)}^2,\dots ,{\left(1/2\right)}^2\right]\right)$

$p_2=$ 1/2, $M_2=\left(3/\mathrm{2,0},\dots ,0\right)$, $R_2=diag\left(\left[{\left(1/2\right)}^2,\dots ,{\left(1/2\right)}^2\right]\right)$

8) skewed bimodal

$p_1=$ 3/4, $M_1=\left(0,\dots ,0\right)$, $R_1=I=diag\left(\left[1,\dots ,1\right]\right)$

$p_2=$ 1/4, $M_2=\left(3/\mathrm{2,0},\dots ,0\right)$, $R_2=diag\left(\left[{\left(1/3\right)}^2,\dots ,{\left(1/3\right)}^2\right]\right)$

9) trimodal

$p_1=$ 9/20, $M_1=\left(-6/\mathrm{5,0},\dots ,0\right)$, $R_1=diag\left(\left[{\left(3/5\right)}^2,\dots ,{\left(3/5\right)}^2\right]\right)$

$p_2=$ 9/20, $M_2=\left(6/\mathrm{5,0},\dots ,0\right)$, $R_2=diag\left(\left[{\left(3/5\right)}^2,\dots ,{\left(3/5\right)}^2\right]\right)$

$p_3=$ 1/10, $M_3=\left(0,\dots ,0\right)$, $R_3=diag\left(\left[{\left(1/4\right)}^2,\dots ,{\left(1/4\right)}^2\right]\right)$

10) claw

$p_1=$ 1/2, $M_1=\left(0,\dots ,0\right)$, $R_1=I=diag\left(\left[1,\dots ,1\right]\right)$

$p_n=$ 1/10, $M_n=\left(n/2-\mathrm{1,0},\dots ,0\right)$, $R_n=diag\left(\left[{\left(1/10\right)}^2,\dots ,{\left(1/10\right)}^2\right]\right)$, $n=$ 0, …, 4

11) double claw

$p_1=$ 49/100, $M_1=\left(-\mathrm{1,0},\dots ,0\right)$, $R_1=diag\left(\left[{\left(2/3\right)}^2,\dots ,{\left(2/3\right)}^2\right]\right)$

$p_2=$ 49/100, $M_2=\left(\mathrm{1,0},\dots ,0\right)$, $R_2=diag\left(\left[{\left(2/3\right)}^2,\dots ,{\left(2/3\right)}^2\right]\right)$

$p_n=$ 1/350, $M_n=\left(n-3/\mathrm{2,0},\dots ,0\right)$, $R_n=diag\left(\left[{\left(1/100\right)}^2,\dots ,{\left(1/100\right)}^2\right]\right)$, $n=$ 0, …, 6

12) asymmetric claw

$p_1=$ 1/2, $M_1=\left(0,\dots ,0\right)$, $R_1=I=diag\left(\left[1,\dots ,1\right]\right)$

$p_n=2^{1-n}/31$, $M_n=\left(n+1/\mathrm{2,0},\dots ,0\right)$, $R_n=diag\left(\left[{\left(2^{-n}/10\right)}^2,\dots ,{\left(2^{-n}/10\right)}^2\right]\right)$,

$n=$ –2, …, 2

13) asymmetric double claw

$p_j=$ 46/100, $M_j=\left(2j-\mathrm{1,0},\dots ,0\right)$, $R_j=diag\left(\left[{\left(2/3\right)}^2,\dots ,{\left(2/3\right)}^2\right]\right)$, $j=$ 0, 1;

$p_n=$ 1/100, $M_n=\left(-n/\mathrm{2,0},\dots ,0\right)$, $R_n=diag\left(\left[{\left(1/100\right)}^2,\dots ,{\left(1/100\right)}^2\right]\right)$, $n=$ 1, 2, 3;

$p_k=$ 1/100, $M_k=\left(k/\mathrm{2,0},\dots ,0\right)$, $R_k=diag\left(\left[{\left(1/100\right)}^2,\dots ,{\left(1/100\right)}^2\right]\right)$, $k=$ 1, 2, 3.

14) smooth comb: $p_n=2^{5-n}/63,M_n=\left(65-96{\left(1/2\right)}^n/\mathrm{21,0},\dots ,0\right),$

$R_n=diag\left(\left[32/63/2^{2n},\dots ,32/63/2^{2n}\right]\right)$, $n=$0,…, 5.

15) discrete comb

$p_n=$ 2/7, $M_n=\left(12n-15/\mathrm{7,0},\dots ,0\right)$, $R_n=diag\left(\left[{\left(2/7\right)}^2,\dots ,{\left(2/7\right)}^2\right]\right)$, $n=$ 0, 1, 2;

$p_k=$ 1/21, $M_k=\left(2k/\mathrm{7,0},\dots ,0\right)$, $R_k=diag\left(\left[{\left(1/21\right)}^2,\dots ,{\left(1/21\right)}^2\right]\right)$, $k=$ 8, 9, 10.

These densities have been carefully chosen because they thoroughly represent many different types of challenges to curve estimators. The first five represent different types of problems that can arise for unimodal densities. The rest of the densities are multimodal. Densities from 6 to 9 are mildly multimodal and one might hope to be able to estimate them fairly well with a data set of a moderate size.

The remaining densities are strongly multimodal and for moderate sizes it is difficult to recover even their shape. Yet, they are well worth studying because the issue of just how many of them can be recovered is an important one. The claw density, 10, is of special interest as this is where the surprising result of local minima in the mean integrated square error occurs. The double claw density, 11, is essentially the same as 6, except that approximately 2 % of the probability mass appears in the spikes. The asymmetric claw and double claw densities, 12 and 13, are modifications of 10 and 11, respectively. The smooth and discrete comb densities, 14 and 15, are enhancements of the basic idea of separated bimodal, 7. Both of these are shown because they have much different Fourier transform properties, since 14 has essentially no periodic tendencies, while 15 has two strong periodic components.

Note that univariate case of this set of models is similar to collection suggested by Marron and Wand in 1992 [12].

In the simulation study, low-size and moderate-size samples (16, 32, 64, 128, 256, 512, 1024) were used. 10000 replications were generated in each case. The conclusions presented below are based on the analysis of these medians and minimums. The estimation accuracy is measured by the mean absolute percentage error:

5. Results of the study

The results of univariate kernel density estimation are examined in detail by Ruzgas and Drulyte, 2013 [1]. The experimental research showed that some of kernel density functions used with multiple distributions mixtures lead to particularly good results. For example, Triweight kernel density function is characterized as one of the most effective when the study is done by using “Discrete comb” mixture with sample size bigger than 256, and dimension equal to 2. The results obtained with Epanechnikov kernel density function have shown that this function is appropriate to be used when the calculations are carried out with the average sample size by using “Bimodal”, “Separated bimodal” and “Smooth comb” mixtures with dimension equal to 2. In addition, the new kernel density function proposed by authors of this research has also shown unexpected results. The smallest median errors for all sample sizes when dimension is equal to 2, are obtained by using the mean average percentage error (MAPE) even at five different mixtures: “Gaussian”, “Skewed unimodal”, “Strongly skewed”, “Kurtotic unimodal”, “Outlier”. Meanwhile, when the sample size is less or equal to 256, the smallest median errors are obtained with “Bimodal”, “Separated bimodal”, “Smooth comb” and “Discrete comb” mixtures. Another important point is that the new kernel density function gives us the smallest median errors with all mixtures of Gaussian distribution and all sample sizes when the dimension is equal to five. The second effective function is Gaussian kernel density function.

The errors dependences on sample size and selected dimension are shown in Fig. 1. Here the Gaussian, Epanechnikov, Triweight and new kernel density functions are marked as G, E, T and N show the results of estimation accuracy. Medians and minimums of mean average percentage errors are marked by solid and dashed lines. The results of errors dependences on sample size results got by using “Skewed bimodal” mixture and different dimensions are shown in Fig. 1.

Fig. 1Estimation accuracy based on MAPE for skewed bimodal bi-variate and quinta-variate densities (here MAPE means the mean absolute percentage error; n is the sample size; the Gaussian, Epanechnikov, Triweight and new kernel density functions are marked as G, E, T and N)

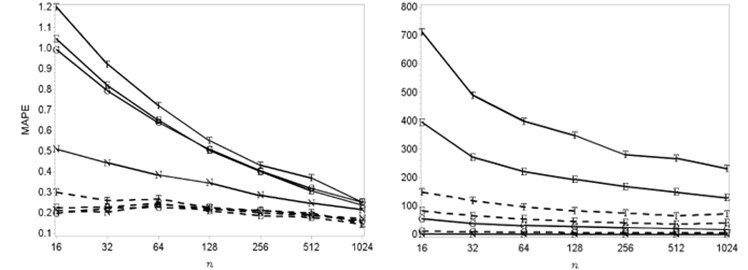
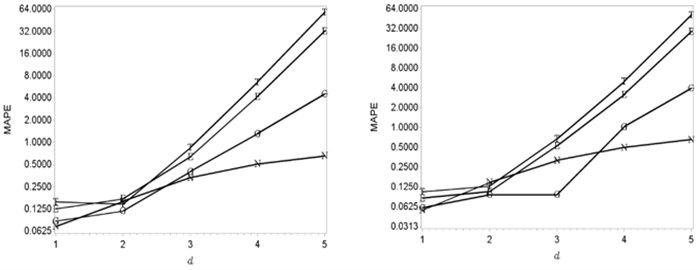
When the dimension is increasing the smallest errors are getting by using new kernel density function. Meanwhile, the Gaussian kernel density function is respectively appropriate to be used when the dimension is smaller or equal to 4 and smaller than 3 in the case of the Epanechnikov and Triweight functions. The effectiveness of the Gaussian kernel density function is shown in Fig. 2.

Fig. 2The relationship between number of dimension and MAPE (Gaussian densities with sample sizes 512 and 1024). Here MAPE means the mean absolute percentage error; d is the dimension; the Gaussian, Epanechnikov, Triweight and new kernel density functions are marked as G, E, T and N

6. The application of goodness fit of test

The set of real clinical data was used as an empirical example (see Fig. 3). Within this section a set of values (the sample size was equal to 52 observations) of the skin lesions previously used for clinical decision support by non-invasive ultrasonic measurements in vivo and histological evaluation ex vivo of their thickness and malignancy after surgical excision has been obtained and compared. The analysis was performed retrospectively in an empirical context in order to estimate the goodness of fit tests.

Histological and ultrasonic data have been collected at the Department of Skin and Venereal Diseases of Lithuanian University of Health Sciences (LUHS). The study was approved by regional ethics committee; the collection of all data was approved by the institutional review board after patients’ informed consent was obtained in accordance with the Declaration of Helsinki Protocols. The data used in the empirical example were acquired on 52 suspicious melanocytic skin tumours (MST) which included 46 melanocytic nevi and 6 melanomas. Inclusion criteria of the study covered size of the tumour up to 1 cm in diameter and histological thickness of ≤1.5 mm.

Fig. 3The results of histological measurements and measurements made by ultrasonic diagnosis

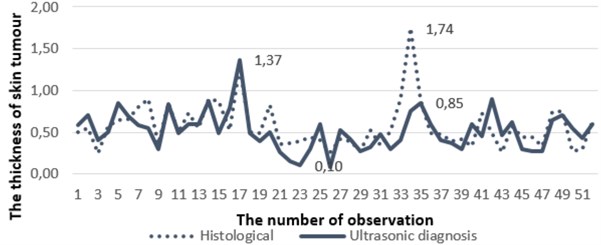
During non-invasive ultrasonic measurements of human skin DUB-USB ultrasound system (“Taberna pro medicum”) of 22 MHz was used for transmission and reception of ultrasonic waves. The immersion experimental set-up with mechanically scanned ultrasonic transducer was employed. The transducer was focused at the surface of the skin. In addition, the system was used for acquisition, digitization and transfer to personal computer the received A-scan ultrasonic signals. The set of acquired A-scan signals were used for reconstruction of the B-scan image. Finally, the maximal thickness of the skin lesion was manually evaluated by a well-experienced dermatologist measuring the distance between the lower edge of the entry echo and the deepest point of the posterior margin of the hypoechoic zone. During the evaluation of thickness, the value of ultrasound velocity was assumed to be 1580 m/s.

After a surgical excision and during the routine histopathology the vertical distance from the uppermost level of the stratum granulosum in the epidermis to the lowest point of the lesion without infiltrate (histological tumour thickness, Breslow index) was independently evaluated by two pathologists and averaged.

More details about ultrasonic examinations in dermatology and comparison with histological data are provided by Jasaitiene et al. in 2011 [44] and Kučinskienė et al. in 2014 [45].

For the goodness of fit we are using some tests based on kernel density estimators described above. Let $X_1,\dots ,X_n$ be a sample of independent observations of a random variable $X$ with unknown probability density function $f\left(x\right)$, $x\in R$. For the given sample it is required to test the hypothesis mentioned in publication made by Rudzkis and Bakshaev in 2013 [46]:

$H_0:f\left(x\right)=f_0\left(x\right)$, against alternative $H_1:f\left(x\right)=\left(1-ϵ\right)f_0\left(x\right)+ϵg\left(x\right).$

Here $f_0\left(x\right)$ is a given probability density function, $\mathrm{ϵ}$ is negligible and $ϵg\left(x\right)$ is an arbitrary distribution, where ${\sigma }_g^2\le {\sigma }_{f_0}^2$ and ${\sigma }_f^2$ is a variance of distribution f.

In this study five tests of goodness of fit have been tried: Pearson's chi-squared test, Rudzkis-Bakshaev’s test, Kolmogorov–Smirnov test, Cramer von Mises test and Kuiper’s test for four different kernel functions. One of the steps leading to the main result was to check the goodness of fit between the density of ultrasonic thicknesses distribution and density of histological thicknesses distribution of the skin tumours. The next step was to compare the compatibility of likely density of histological thicknesses distribution of the skin tumours and Normal distribution density. If two mentioned checked conditions are satisfied, as a result it is clear that the density of ultrasonic thicknesses distribution and Normal distribution density are interconnected. All results of the goodness of fit between the density of ultrasonic thicknesses distribution and density of histological thicknesses distribution of the skin tumours (denoted as U H) and the goodness of fit between the density of histological thicknesses distribution and Normal distribution density (denoted as H N) are shown in Table 2.

7. Conclusions

Within the performed study the check of the goodness of fit test for thicknesses of the skin tumours measured in two different ways (non-invasive ultrasound examination and invasive histological analysis). The performed simulation study leads to the kernel $K$ which has shown a better performance for Gaussian mixtures with considerably overlapping components and multiple peaks (double claw distribution). In addition, its accuracy decreases more slowly than the other kernels, when the random vector dimension increases. The empirical study has shown that Pearson’s chi-squared test is the most sensitive of all used tests. The main reason is the differences between empirical and theoretical distributions due to heavy tails of the empirical distributions. As a result, the Kuiper’s test has the lowest sensitivity criteria and was the most powerful in performed comparative analysis. The obtained results have shown that the density of ultrasonic thicknesses distribution is similar to the Normal distribution density more than 90 percent. Hence, the reliability of ultrasonic thickness measurement of the skin tumour is completely covered by high similarity to the histological thickness measurement, which is known as a golden standard in the field of dermatology. Also the application of goodness fit of test has shown that p-value of all criteria’s with all kernel functions are approximately 2 times bigger than Pearson’s chi-squared test. Therefore, it proves that the application of non-invasive ultrasonic technique (at least of 22 MHz) for thickness estimation of the melanocytic skin lesions (tumours and nevus) possesses high reliability and is suitable to be used in daily clinical practise.