Measurement of large amplitude plane vibrations of two dimensional structures

1. Introduction

In the paper large amplitude plane vibrations of an elastic structure are investigated experimentally by using the method of time averaged geometric moiré. Investigations of a two-dimensional problem are performed. Experimental setup is developed and the results obtained by using the experimental procedure are analyzed. On the basis of a one-dimensional model graphical relationships for linear variation with respect to longitudinal coordinate of amplitude of vibrations are obtained. They provide the background for interpretation of partially exposed time averaged moiré. Recommendations for the choice of background intensity are provided.

This paper continues the analysis of time averaged moiré techniques presented in [1]. Similar problems are analyzed in [2-17] and in a number of other similar papers.

2. Experimental measurements of large amplitude vibrations

The investigated elastic structure with moiré lines attached to the vibroexciter is shown in Fig. 1.

Experimental time averaged image is shown in Fig. 2.

Part of the zoomed image of Fig. 2 is shown in Fig. 3. Time averaged moiré lines for large amplitude vibrations are seen in it.

This image shows that partially exposed moiré lines can be used for the measurement of large amplitude vibrations.

Fig. 1The investigated elastic structure with moiré lines attached to the vibroexciter

Fig. 2Experimental time averaged image for frequency of excitation 9 Hz

Fig. 3Part of the zoomed image of Fig. 2

3. Theoretical investigation of the time averaged partially exposed measurement of vibrations

This investigation is based on the use of the one-dimensional model.

Intensity of the time averaged partially exposed image is represented as:

where ${\stackrel{-}{I}}_b$ is the intensity of the time averaged partially exposed image, $m$ is a large integer number, $b$ is the background intensity, $\theta$ is the cutting parameter, $\lambda$ determines the width of moiré lines, $x$ is the coordinate of a point of a one-dimensional structure in the status of equilibrium, $u$ is the displacement and:

and it is assumed that:

where $k$ is a constant.

Fig. 4I-0, I-1/2 and I-1 when θ=0⋅π/4

Fig. 5I-0, I-1/2 and I-1 when θ=1⋅π/4

Fig. 6I-0, I-1/2 and I-1 when θ=2⋅π/4

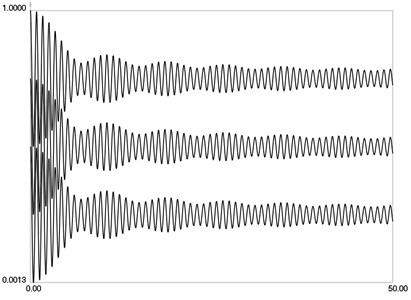
Fig. 7I-0, I-1/2 and I-1 when θ=3⋅π/4

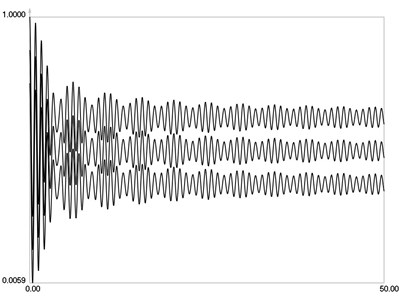
Fig. 8I-0, I-1/2 and I-1 when θ=4⋅π/4

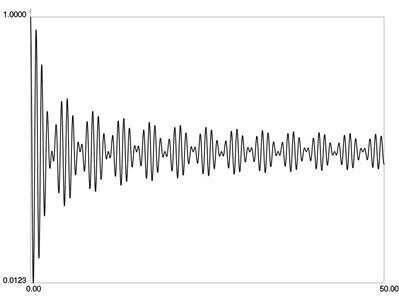
In the performed investigation parameters have the values: $\lambda =\text{0.8}$ and $k=\text{0.1}$.

${\stackrel{-}{I}}_0$, ${\stackrel{-}{I}}_{1/2}$ and ${\stackrel{-}{I}}_1$ when $\theta =0\cdot \pi /4$ are graphically shown in Fig. 4.

${\stackrel{-}{I}}_0$, ${\stackrel{-}{I}}_{1/2}$ and ${\stackrel{-}{I}}_1$ when $\theta =1\cdot \pi /4$ are graphically shown in Fig. 5.

${\stackrel{-}{I}}_0$, ${\stackrel{-}{I}}_{1/2}$ and ${\stackrel{-}{I}}_1$ when $\theta =2\cdot \pi /4$ are graphically shown in Fig. 6.

${\stackrel{-}{I}}_0$, ${\stackrel{-}{I}}_{1/2}$ and ${\stackrel{-}{I}}_1$ when $\theta =3\cdot \pi /4$ are graphically shown in Fig. 7.

${\stackrel{-}{I}}_0$, ${\stackrel{-}{I}}_{1/2}$ and ${\stackrel{-}{I}}_1$ when $\theta =4\cdot \pi /4$ are graphically shown in Fig. 8.

For conventional time averaged moiré, the envelope function has the form:

where $J_0$ is the zero order Bessel function of the first kind.

For partially exposed time averaged moiré the envelope function has the form:

where ${\stackrel{-}{J}}_0$ is the modified zero order Bessel function of the first kind, $\theta$ is the cutting parameter, $b$ is the background parameter.

From the presented graphical relationships qualities of the modified zero order Bessel function of the first kind are seen. They enable to interpret partially exposed time averaged moiré images.

From the presented results it is recommended to choose the background intensity as:

This has the advantage in the interpretation of experimental results because the intensity values are not shifted towards black or white.

4. Conclusions

Large amplitude plane vibrations of an elastic structure are investigated experimentally. Experimental setup is developed and the results obtained by using the experimental procedure are analyzed. On the basis of obtained experimental results it is shown that partially exposed moiré lines can be used for the measurement of large amplitude vibrations.

On the basis of a one-dimensional model graphical relationships for linear variation with respect to longitudinal coordinate of amplitude of vibrations are obtained. They provide the background for interpretation of partially exposed time averaged moiré.

From the presented graphical relationships qualities of the modified zero order Bessel function of the first kind are seen. They enable to interpret partially exposed time averaged moiré images.

From the presented results it is recommended to choose the background intensity as grey color exactly in the middle between black and white. This has the advantage in the interpretation of experimental results because the intensity values are not shifted towards black or white.

The obtained results are used for the analysis and measurement of large amplitude vibrations of mechanical devices, especially when high precision is required.