Sliding mode control of a 2-DOF manipulator with random base vibration based on modified exponential reaching law

1. Introduction

With the gradual improvement of robot technology, manipulators are widely applied to many fields of science, such as ammunition loading manipulators in tank weapon [1], free floating space manipulators in astronautics [2], underwater robot manipulators for ocean development [3]. The problems about dynamics and control of these type of manipulators have drawn extensive concern of researchers from all over the world. Manipulators working in different environments may be affected by various uncertain factors, such as random vibration of base, model uncertainty due to the lack of cognition, understanding deviation, simplification and assumptions in modeling process, etc. The presence of these factors make the precision and stability be the main difficulty in the control problem of manipulators. To eliminate the influence of these nonlinear factors, different kinds of advanced control methods have been applied to the control of corresponding manipulators.

Soltanpour M. R. [4] designed an optimal fuzzy sliding mode controller based on particle swarm optimization algorithm for tracking the robot manipulator whose model has structured and unstructured uncertainties. Akira Abe [5] proposed a minimum energy trajectory planning method based on a multi-objective optimization technique to solve the point-to-point motion task of a robot manipulator, which mounted on flexible base, and effectively suppressed the residual vibration of the manipulators’ flexible base. Toda and his team deeply studied the control problems of manipulators [6-8] with oscillatory bases. These manipulators were installed on vessels or ocean structures. In these papers, the controller was designed by combining the $H_{\mathrm{\infty }}$ control method with PD control method, and it worked based on the assumption that the frequency of the base oscillation had been known.

Literatures above has done a lot of research on manipulators control with different methods, but the objective of paper [4] were manipulators with fixed base. The nonlinearities caused by base vibration which have great influence on manipulators’ dynamical performance were not considered. Paper [5] studied the control problems of manipulators with flexible vibration base. Papers [6-8] studied the control problems of manipulators whose base oscillation frequency had been known. In this paper, the base vibration is caused by external force, and it is random. That is to say the frequency of base vibration is unknown. Therefore, methods from literatures above are not suitable in this case.

Considering the problems analyzed above, a sliding mode control based on modified exponential reaching law is studied in this paper to reach the position control task of a 2-DOF manipulator with external random vibration base. The dynamic model is established by using the second kind Lagrange equation first. In the dynamic model, the nonlinear term caused by base vibration is presented as the system uncertain disturbance. Then, the sliding mode controller is designed, and the reaching law and control algorithm are analyzed in detail. Finally, a Simulink simulation model is established to verify the feasibility of the control method.

2. Dynamic model of 2-DOF manipulator with base vibration

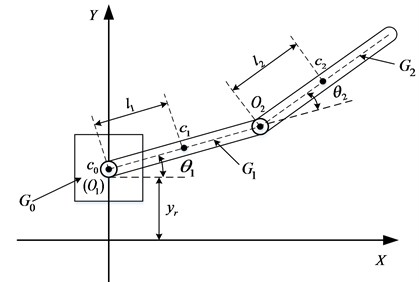
The simplified mathematic model of a 2-DOF manipulator with vertical vibration base is as shown in Fig. 1. Here, $XOY$ donates Cartesian coordinate system; $G_0$ is the base for fixing the manipulator; $G_1$, $G_2$ are link 1 and link 2, respectively; $O_i$ ($i=1,\mathrm{}2$) are the rotation center of link $i$; $c_i$ ($i=$0, 1, 2$)$ are the mass center of $G_i$; ${\theta }_1$ is the angular displacement of link 1 relative to the horizontal direction; ${\theta }_2$ is the angular displacement of link 2 relative to link 1; $l_i$ ($i=$1, 2) are the distance between the mass center and the rotation center of link $i$.

Fig. 1Simplified model of the 2-DOF manipulator

Assume the mass of link $i$ are $m_i$; the rotational inertia of link $i$ relative to rotation center $O_i$ are $I_i$; define generalized coordinate vector as $\mathbf{q}={\left(q_0,q_1,q_2\right)}^T={\left(y_r,{\theta }_1,{\theta }_2\right)}^T$, using the second kind Lagrange equation to establish the dynamical model as follow:

In Eq. (1):

3. Sliding mode controller design

3.1. Reaching law design

The motion of sliding mode control system is a two-pronged process: the reaching process and the sliding mode process. In the reaching process, the trajectory of the system is outside the switching surface or move through the switching surface within the limited time in state space. In the sliding mode surface, the system moves near the sliding surface and sliding along the switching surface. From the principle of sliding mode variable structure, we can know that the reaching condition of sliding mode control can only ensure the controlled object reach the switching surface in finite time from the arbitrary initial state. So, we can use different reaching laws to improve the dynamic quality in the reaching process. The typical reaching laws include constant reaching law; exponential reaching law; power reaching law, and etc. [9]. In these reaching laws, the expression of exponential reaching law is as shown in Eq. (2):

2

$\dot{s}=-\epsilon \mathrm{s}\mathrm{g}\mathrm{n}s-ks,\epsilon >0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}k>0.$

Sliding mode control methods based on the traditional reaching laws are limited somehow because the existence of chattering. One reason is that the parameters in these reaching laws cannot change with system state. In this paper, a sliding mode control algorithm based on exponential reaching law is chosen to shorten the reaching time and decrease the reaching rate to the switching surface, so as to improve the dynamic quality. To avoid the chattering when the system moves nearby the switching surface, we bring a $s^{\beta }$ factor in exponential reaching law, so the modified reaching law is as follow:

3

$\dot{s}=-\epsilon s^{\beta }\mathrm{s}\mathrm{g}\mathrm{n}s-ks,\epsilon >0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}k>0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\beta >0.$

Fig. 2Contrast of reaching law curve with different β

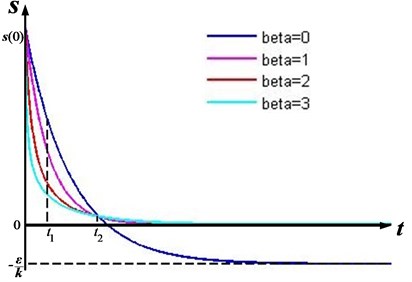
As it shows in Fig. 2, after introducing the factor $s^{\beta }$, the rate of reaching law curve is greater than the original one during $0<t<t_1$, and less than the original one during $t_1<t<t_2$. This means, the rate of the system can be smaller when reaching the switching surface $s=\text{0}$ if the $s^{\beta }$ is introduced. And it is obviously that the greater the $\beta$ is, the greater the difference of the rate among the reaching law curve will be. Therefore, control algorithm based on the modified exponential reaching law can shorten the time of the reaching process as well as reduce the reaching speed when the system comes by sliding surface, and the chattering when the system reaching the sliding surface can be effectively decreased.

Based on the modified exponential reaching law, an attenuation factor is added into Eq. (3) as refer to paper [10]. So the new reaching law can be written as:

4

$\dot{s}=-\epsilon s^{\beta }{e}^{-\alpha t}\mathrm{s}\mathrm{g}\mathrm{n}s-ks,\epsilon >0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}k>0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\alpha >0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\beta >0.$

4. Simulation results

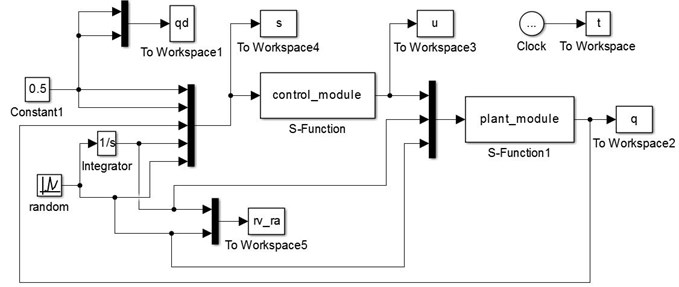
To verify the effectiveness of the controller based on modified exponential reaching law, a Simulink simulation model is established as Fig. 3 shows.

Fig. 3Simulink simulation model

The target angular displacements of link 1 and link 2 are $q_{1d}=\mathrm{}$0.5 rad, $q_{2d}=\mathrm{}$0.5 rad, and the initial state of system is $\left[q_1{\dot{q}}_1\mathrm{}\mathrm{}\mathrm{}{q}_2\mathrm{}\mathrm{}\mathrm{}{\dot{q}}_2\right]=[0\mathrm{}\mathrm{}\mathrm{}0\mathrm{}\mathrm{}\mathrm{}0\mathrm{}\mathrm{}\mathrm{}0$. The value of control parameters are $c_1=c_2=\text{20}$, $k=\text{10}$, $\epsilon =\text{0.5}$, $\alpha =\text{1}$, $\beta =\text{2}$. The value of $\mathbf{f}$ is $\mathbf{f}={\left[3\mathrm{s}\mathrm{i}\mathrm{n}\left(\pi t\right)3\mathrm{c}\mathrm{o}\mathrm{s}\left(\pi t\right)\right]}^T$. The mass and structure parameters are as shown in Table 1.

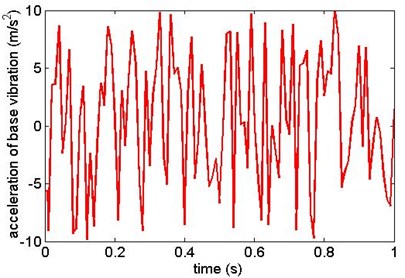
The amplitude of random base vibration acceleration is 10 m/s², which means $A\left({\ddot{q}}_0\right)=$ 10 m/s², and the base vibration curve is as shown in Fig. 4.

Fig. 4Base vibration acceleration

The simulation results are as shown from Figs. 5-12. Fig. 5 and Fig. 6 are the angular displacement of link 1 and link 2; Fig. 7 and Fig. 8 are the angular velocity of link 1 and link 2; Fig. 9 and Fig. 10 are the generalized control torque acting on link 1 and link 2.

Fig. 5Angular displacement of link 1

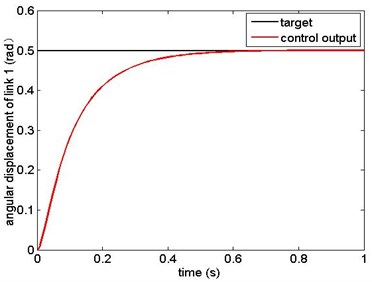
Fig. 6Angular displacement of link 2

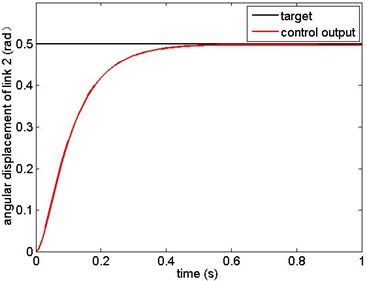
Fig. 7Angular velocity of link 1

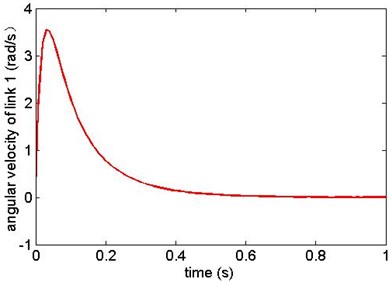
Fig. 8Angular velocity of link 2

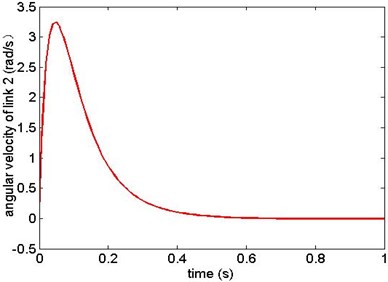
The simulation results show that the sliding mode controller based on modified exponential reaching law in this paper can overcome the influence of model uncertainty and random base vibration. The manipulator reaches the target state precisely in 0.6 s from the given initial state. This results prove that the controller has high precision of location and has good robustness.

Fig. 9Generalized control torque 1

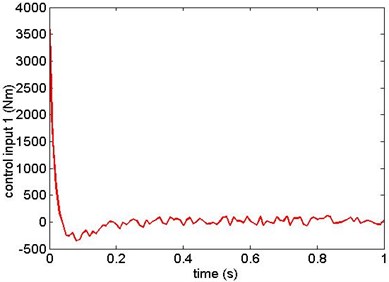
Fig. 10Generalized control torque 2

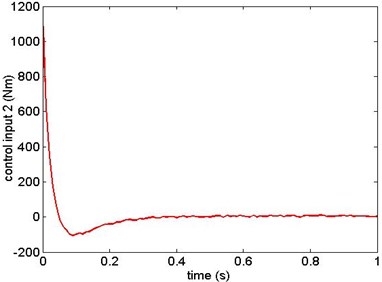
5. Conclusions

In this paper, the dynamic model of 2-DOF manipulator with random base vibration is established by using the second kind Lagrange equation. Then the nonlinear term generated by base random vibration is presented as external disturbance. The unmodeled error and parameters uncertainty are presented as model error disturbance. A sliding mode controller based on modified exponential reaching law is designed base on the dynamic model of system. When compared with the traditional exponential reaching law, the modified one can make the system have higher reaching speed in the earlier process and have lower speed in the later process. This not only ensure the rapidity of reaching process, but also decrease the chattering when the system reaching the sliding surface. It is verified that the controller can realize the rapidly and precisely control of the 2-DOF manipulator under random base vibration.