Free vibration study of v-shape and rectangular shape double-sided cracks in a cantilever beam

1. Introduction

In order to identify the damage in structures by vibration monitoring, the study of the changes of the structural dynamic behavior due to cracks is required for developing the detection criterion. Some earlier research based on the open crack model, which assumes cracks always remain open during the vibrating instance, has been proposed. For example, the effect of discontinuities in stiffness on the natural frequencies of slender bars was investigated by Thomson [1]. The discontinuity of the bending stiffness was caused by a slot not a crack, hence the stress concentration was not considered in Thomson’s model. Gudmundson [2] used the perturbation method to compute the frequency changes of cantilever beams due to cracks. The natural frequencies were in good agreement with the experimental results from Wendtland [3] for the beams with small crack size. Later, Gudmundson [4], Yuen [5], Gounaris and Dimarogonas [6] and several other researchers proposed a more precise method based on the ‘line spring’ model [7, 8] in fracture mechanics. The idea was to model the crack by using ‘flexibility scalars’ or a local flexibility matrix, which could be a 2×2, or 4×4, or 6×6 matrix, connecting longitudinal, bending and shear forces and displacements near the crack-tip area. The local flexibility scalars and matrices were formulated from the stress intensity factors of the cracked structures considered. However, these stress intensity factors can be determined analytically or by experimental testing only for simple structures. In general, they have to be evaluated by numerical techniques such as the finite element method. In addition to the above approaches, several studies were done on the problems of vibrations of cracked beams under the simple beam theory. Christides and Barr [9] derived the equation of bending motion for a Bernoulli-Euler beam with pairs of symmetric cracks. They used an exponential type function (the so-called ‘crack function’) to model the stress concentration near the crack tip. Christides and Barr proposed a two-term Rayleigh-Ritz solution to their equation of motion to evaluate the fundamental natural frequency of a simply supported beam with rectangular cross-section and a pair of mid-span cracks. However, Shen and Pierre [10] found that Christides and Barr’s original solution was not fully converged and hence a modified Galerkin expansion was proposed in order to improve the solution convergence. Performance of machines changes due to the presence of cracks. Most of the failures of presently used equipments are mainly due to limited fatigue strength. So, detection of crack and taking preventive measures on defective structures is of most importance and it has been carried out throughout the world in many research institutes [13-20].

The design life of most of the power equipments is of 30 years, it means that after 30 years, they will be on the way of failure. It is expected that failures due to low-cycle fatigue initiated cracks will be a major cause of machine failures. For on-line crack detection and monitoring the development of methods started in the early 1970s in the power industry. Dimarogonas [21, 22], in two internal reports of the General Electric Co., Turbine Department, developed the theory of vibration of cracked shafts, an outline of which and the extension to cracked beams and turbine blades were included in a textbook [23]. Pafelias [24] continued Dimarogonas’ work after 1972 and in a formal General Electric report (published in the Technical Information Series) used the theory, and extensive laboratory and field experiments to develop a methodology for crack detection based on the 2X harmonic and the half critical speed subharmonic. He further reported on the development of an on-line electronic instrument for monitoring and early warning of cracked rotors to be used as a turbine supervisory instrument. Pafelias' report [24] had wide distribution and triggered substantial further work in the turbo machinery industry. Since the early 1980s there has been a substantial body of academic research on the subject. There is a number of reports describing field experience related to the vibration of cracked structures, by Schmerling and Hammond [25], Haas [26], Jack and Patterson [27], Greco et al. [28], Kottke and Menning [29], Anifantis et al. [30], Klompas [31] and Kraemer et al. [32]. Reviews on the dynamic response of cracked structures were reported by Dimarogonas and Paipetis [33], Wauer [34], Entwistle and Stone [35], Dimarogonas [36] and Gasch [37].

For a stepped rotor, Dimarogonas [21, 22] used a transfer matrix technique to compute the change in critical speed of a shaft due to the crack. The results confirmed the finding that for small crack depths the change in critical speed is proportional to ${\left(a/D\right)}^2$, e.g. an edge crack with depth 54 % of the radius produced a 5.6 % (overestimated) change in the lowest critical speed of the shaft. It was concluded that measurement of the change in critical speed was not an efficient way to monitor rotor cracks. Wendtland [40] reported in his dissertation on an extensive experimental program for the calculation of the change of natural frequencies of beams of different geometries and boundary conditions using machined slots to simulate cracks. Wendtland computed the cracked section flexibility from a crude simple beam analysis of the reduced section. Even though he clearly stated that his results were not appropriate to real cracks, only to saw-cuts, there was some confusion later-on because several authors compared finite element analysis results, modeling the crack with a dense grid rather than a special cracked element, and reported agreement with Wendtland, naturally, because their model was also a notched beam. Tsalik [41], Petroski and Glaszik [42], Petroski [43-50], Kumar and Petroski [51], and Ku and Shen [52] used the equivalent slot approach of Kirmsher [38] and Thomson [39], to solve vibration problems of damaged beams and other stationary damaged structures, modeling the damage (or crack) with a local member of reduced cross-section. The analytical method for the computation of the dynamic response of cracked Euler-Bernoulli beams by modeling the cracked region as a local flexibility found with fracture mechanics methods was first discussed in a textbook by Dimarogonas [23], with applications to cracked turbine blades.

The cracked Euler-Bernoulli beam vibration theory and extensive analytical and experimental results on the natural frequencies and vibration modes of simple continuous and lumped mass beams with surface cracks were introduced from the mid-1970s by Chondros [53, 54], and Chondros and Dimarogonas [54, 55]. They used the local flexibility concept and the fracture mechanics approach for its computation.

Most of the research has been carried out the analysis of the effect of single crack on the dynamics of the simple structures. From the detailed literature survey, it has been observed that most of the researchers have worked on the cracked cantilever beam. They have investigated the effect of crack locations and crack depths on different vibrating properties like natural frequency and resonance amplitude. None of the researchers has worked on two open double sided rectangular shape cracks on the cantilever beam of square cross section. Action of cyclic loads leads to formation of double sided cracks on the beam. Also in the literature [11], different cracked cross section (rectangular shape, v-shape) is mentioned. Previously, mathematical model was developed by W. M. Ostachowicz and M. Krawczuk [12] for the cantilever beam which has two open double-sided v shape cracks. On the other hand, there should be existence of the mathematical model which may be used to determine the characteristics roots of a cantilever beam which has two open double sided rectangular shape cracks. Hence in this study, the mathematical model developed by W. M. Ostachowicz and M. Krawczuk for v shape crack is checked for rectangular shape crack to see the flexibility of the theory presented by W. M. Ostachowicz and M. Krawczuk. Also, the effect of two double-sided cracks on the characteristics roots is studied. It is very essential to understand the dynamics of the cracked cantilever beam for the specific configurations because the natural frequency is used as basic criteria for predicting the location and the size of the damage.

2. Mathematical model

W. M. Ostachowicz and M. Krawczuk are presented a method of analysis of the effect of two open cracks on the bending mode natural frequencies in a cantilever beam. W. M. Ostachowicz and M. Krawczuk considered two types of cracks in their study, double sided and single sided cracks. Double sided cracks occur in the beam due to the action of cyclic loading and on the other hand, single sided cracks occur in the beam due to fluctuating loads. When cyclic load acts on the smooth beam, then beam gets bent on both the sides, due to which open double-sided cracks occur on the beam due to less fatigue strength of the material or due to some localised manufacturing defect in the beam such as corrosion, corrosion erosion in the beam.

One can take the natural vibration frequencies equation of the beam in the well known form:

where $\rho$ is the material density, $F$ is the cross sectional area of the beam, $y(x,t)$ is the deflection of the beam and J is the geometrical moment of inertia of the beam cross section. By introducing elasticity elements in crack locations one obtains a system of three beams. The equivalent stiffness of the elasticity element is calculated as in Section 2 [12].

The model of the problem is shown in Fig. 1. The boundary conditions, in terms of the non-dimensional beam length $\xi =x/L\text{,}$ can be expressed as follows: $y_1\left(0\right)=0\text{,}$ zero displacement of the beam at the restraint point; $y_1^{\text{'}}\left(0\right)=0$, zero angle of rotation of the beam at the restraint point; $y_1\left(e_1\right)=y_2\left(e_1\right)$, compatibility of the displacement of the beam at the location of the first crack; $y_2^{\text{'}}\left(e_1\right)-y_1^{\text{'}}\left(e_1\right)={\theta }_1{y}_2^{\text{'}}\left(e_1\right)$, total change of the rotation angle of the beam at the location of the first crack; $y_1^{\text{'}\text{'}}\left(e_1\right)=y_2^{\text{'}\text{'}}\left(e_1\right)$, compatibility of the bending moments at the location of the first crack; $y_1^{\text{'}\text{'}\text{'}}\left(e_1\right)=y_2^{\text{'}\text{'}\text{'}}\left(e_1\right)$, compatibility of the shearing forces at the location of the first crack; $y_2\left(e_2\right)=y_3\left(e_2\right)$, compatibility of the displacements of the beam at the location of the second crack; $y_3^{\text{'}}\left(e_2\right)-y_2^{\text{'}}\left(e_2\right)={\theta }_2{y}_3^{\text{'}\text{'}}\left(e_2\right)$, total change of the beam rotation angle at the location of the second crack; $y_2^{\text{'}\text{'}}\left(e_2\right)=y_3^{\text{'}\text{'}}\left(e_2\right)$, compatibility of the bending moments at the location of the second crack ;$y_2^{\text{'}\text{'}\text{'}}\left(e_2\right)=y_3^{\text{'}\text{'}\text{'}}\left(e_2\right)$, compatibility of the shearing forces at the location of the second crack; $y_3^{\text{'}\text{'}}\left(1\right)=0$, zero bending moment at the end of the beam; $y_3^{\text{'}\text{'}\text{'}}\left(1\right)=0$, zero shearing force at the end of the beam. Here $e_1$ and $e_2$ are the distances between the end of the cantilever beam and the crack locations.

Fig. 1Clamped cantilever beam with two open cracks [12]

The solution of Eq. (1) is sought in the form:

Substituting this solution into Eq. (2), after simple algebraic transformation, one has:

where ${\beta }^4={\omega }^2\rho A/L^{4}EJ$.

Taking the function $y\left(\xi \right)$ in the form of a sum of three functions:

And taking into account the boundary conditions one obtains the characteristic equation [12], which is to be solved to determine the characteristic roots. The roots are used for the calculation of natural vibration frequencies:

where ${\omega }_i$ is the $i$th natural vibration frequency of the beam and ${\beta }_i$ is the $i$th characteristic root.

3. Simulated crack configurations

In this study, natural vibrations of a cantilever beam having rectangular shape edge crack are studied. The same geometric and material properties of reference model are taken and are as given below to compare the results of cantilever beam with rectangular shape edge crack cases with v shape edge crack cases.

Geometric properties: The length and cross sectional area of the beam are 1 m and 0.1×0.2 m², respectively.

Material properties: Modulus of elasticity ($E$) is 2.1×10¹¹ N/m², the density ($\rho$) is 7860 kg/m³. The value of poisons ratio is not given in the reference model, so it is assumed as 0.3.

Fig. 2Diagram of a cantilever beam with two open v shape crack [12 ]

Fig. 3Design of a cantilever beam with two open rectangular shape cracks. First crack details: L1/L= 0.1; a1/H= 0.3; Second crack details: L2/L= 0.6; a2/H= 0.5

In present work, total number of specimens considered is 63 and it is same as that of cracked cases of the reference model to study the amount of deviation given by the cantilever beam for v edge cracked cases and rectangular edge cracked cases for the characteristics roots. Two separate cases are considered, in case 1 each specimen has a 2 cracks and each specimen has 4 cracks in case 2. The details of each case are given below.

Case 1: Three specimens are considered in this case. 2 transverse cracks are taken on each specimen by keeping crack location constant at 100 mm from the beam fixed end. At this location, crack depth is taken as 30 mm for one specimen, similarly for next two specimens it is taken as 50 mm, and 70 mm respectively.

Case 2: In this case, 60 specimens are considered. 4 transverse cracks are taken on each specimen. This case is divided into 3 sub cases. Each sub case has 20 specimens. In the first sub case, location of the first crack is at 100 mm and crack depth is taken as 30 mm as mentioned in Fig. 3, then the location of the second crack is varied as 110 mm, 200 mm, 400 mm, 600 mm and 800 mm from the cantilever end and at each location crack depth is taken as 10 mm, 30 mm, 50 mm and 70 mm respectively. Similar configuration is used for next 2 sub cases, but instead of 30 mm crack depth at the first location, 50 mm and 70 mm crack depth is taken for the second and third sub cases respectively.

4. Finite element modelling and analysis

ANSYS 12.1 [56] finite element program is used to determine natural frequencies of the undamaged as well as cracked cases of beams. For this purpose, block of required dimensions is created by volume command. Then at the required locations on the surface of the beam model, two small rectangular areas of required dimensions are created and extruded. Then small volumes are subtracted from large volume of cantilever beam model to obtain three dimensional models with two open cracks. A 20 node structural solid 186 element [57] is selected for the analysis, because of several special features like stress stiffening, large strain, and large deflection. Finite element boundary conditions are applied on the beam to constrain all degrees of freedom of the extreme left hand end of the beam. The Block Lanczos eigenvalue solver is used to calculate the natural frequencies of the beams. Mesh independent study is done for the crack model by taking 3 different mesh sizes like 20 mm, 25 mm and 30 mm and then for each mesh size, result of natural frequency almost remains the same.

By finite element analysis, the natural frequencies of the cracked cases of the beams are determined as shown in Table 1. The values of natural frequencies obtained by FEA for different damaged cases are substituted in Eq. (5) to get the values of characteristics root as shown in Table 2.

Fig. 4Finite element modelling of the cracked beam

Fig. 5Crack zone details of a FEA model

Fig. 6Natural frequency plot, First crack details: L1/L= 0.1; a1/H= 0.5; Second crack details: L2/L= 0.11; a2/H= 0.5

5. Results

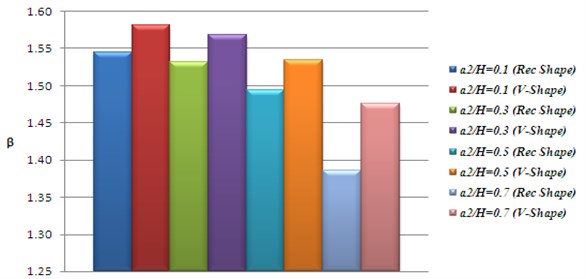
The comparison of the results of characteristics roots for v shape and rectangular shape cracked cases are shown in Figs. 7-9. Total 12 critical cracked cases are shown for the characteristics roots.

From Figs. 7 and 8, it is seen that the value of characteristics roots for v-shape and rectangular shape cracked cases gives good agreement. From Fig. 9, it is noticed that v-shape and rectangular shape cracked cases gives some error for characteristics roots between 1.113 % to 10.549 %. The main advantage of the existing mathematical model is that it gives outstanding results for characteristics roots at critical region of the beam.

Fig. 7Characteristics roots for Rec. shape and V- shape cracks. The first crack: Location L1/L= 0.1; Size a1/H= 0.3; The second crack: Location L2/L= 0.11

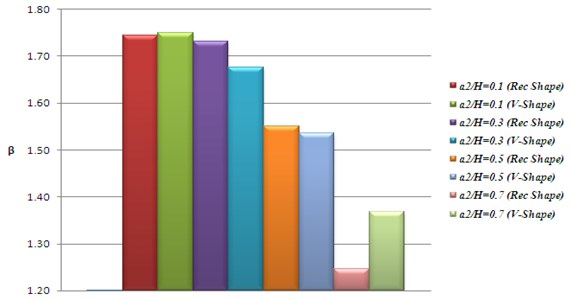
Fig. 8Characteristics roots for Rec. shape and V- shape cracks. The first crack: Location L1/L=0.1; Size a1/H= 0.5; The second crack: Location L2/L= 0.4

From Fig.10, it is found that when the location of the second crack increases from the first crack location by keeping the same location then beam rigidity increases more rapidly. depth of the second crack then value of characteristics root almost remains constant for v shape as well as rectangular shape cracked cases of the beam. This is true when the depth of the second crack is less than 15 % of the total depth ($2H$) of the beam. Constant value of characteristics root means almost constant value of stiffness of the beam.

Fig. 9Characteristics roots for Rec. shape and V- shape cracks. The first crack: Location L1/L= 0.1; Size a1/H= 0.7; The second crack: Location L2/L= 0.11

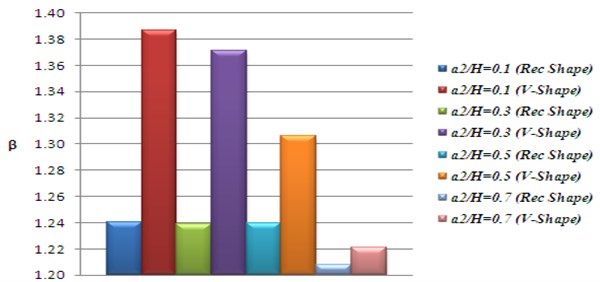
For the same configuration, When the depth of the second crack increases above 30 mm then value of characteristics root increases due to increase in stiffness of the beam materials. It means that as the location of the second crack increases from the first crack

Fig. 10Effect of the second crack upon the characteristics root of the beam with two double sided-cracks. The first crack: location L1/L= 0.1; Size = a1/H= 0.3; β1= 1.7602

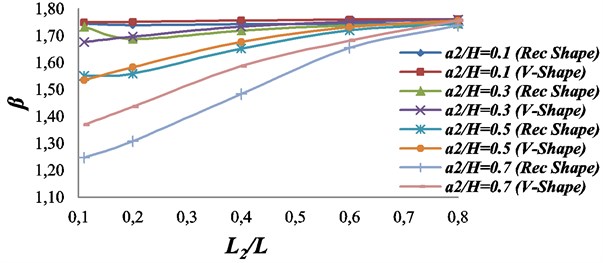
Fig. 11Effect of the second crack upon the characteristics root of the beam with two double sided-cracks. The first crack: location L1/L= 0.1; Size = a1/H= 0.5; β1= 1.5837

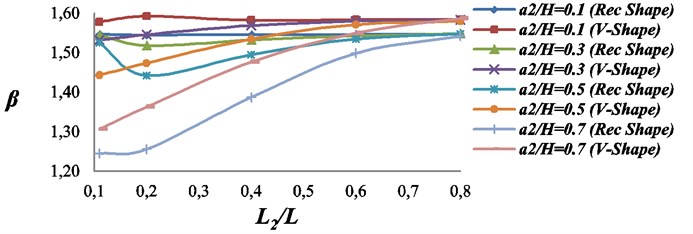
For the same configuration, When the depth of the second crack increases above 30 mm then value of characteristics root increases due to increase in stiffness of the beam materials. It means that as the location of the second crack increases from the first crack location then beam rigidity increases more rapidly.

The values of characteristics roots for v shape and rectangular shape cracked cases gives good agreement when depth of the cracks are less than 25 % of the total depth ($2H$) of the beam.

For larger depth, the found error in the values of characteristics roots for v shape and rectangular shape cracked cases is fairly more, this may be due to lack of width specifications of the v shape crack profile as mentioned in the reference model [12].

The decrease in the value of characteristics root is largest, if cracks are nearer to each other as well as closer to the cantilever end. When the value of characteristics roots are compared for Figs. 10-12, it is found that the value of characteristics roots are minimum due to the presence of largest crack depth of the first crack at the first location as shown in Fig. 12. The reduction in characteristics roots value only due to the presence of largest crack depth at the first location.

Fig. 12Effect of the second crack upon the characteristics root of the beam with two double sided-cracks. The first crack: location L1/L= 0.1; Size = a1/H= 0.7; β1= 1.3906

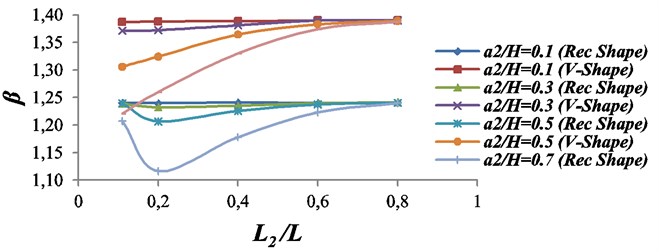
Fig. 13Effect of the second crack upon the characteristics root of the beam with two double sided-cracks. The first crack: location L1/L= 0.1; Size = a1/H= 0.5; β1= 1.5837

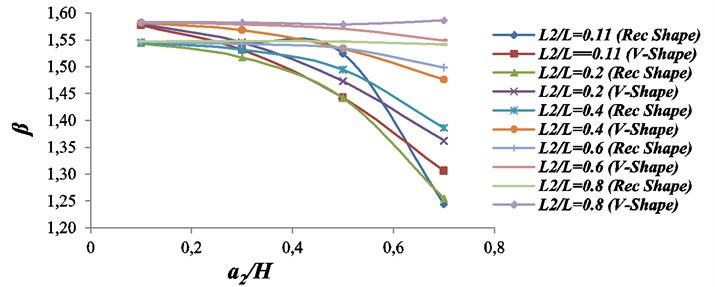
From Fig. 13, it is found that when the depth of the second crack at any location (apart from last location, $L_2/L=$0.8) increases then the value of characteristics root decreases. But decrease in the value of characteristics root is rapid, when second crack location is nearer to first crack location because the effect of damping remains largest in such a cracked case. For the larger crack depths, as the location of the second crack increases from the first crack location then rigidity of the beam increases significantly or vice versa. From Fig. 13, it is also found that the values of characteristics roots for v shape as well as for rectangular shape cracked cases are close to each other. The last location of the second crack ($L_1/L=$0.8) is very nearer to the unconstrained end, hence at this location even though crack depth increases, the value of characteristics roots almost remain constant due to presence of small amount of damping effect in the beam.

6. Conclusions

Analysis focuses on free vibration only. In the FEA part of this study, the effect of the crack depth and location on modal properties of the beam was investigated. The following conclusions can be drawn from the analyses:

1. The theory presented by W. M. Ostachowicz and M. Krawczuk for the cantilever beam which has two open double-sided v shape cracks is applicable for the same beam which has two open double-sided rectangular shape cracks.

2. Up to 50 mm crack depth, the values of characteristics roots for v shape and rectangular shape cracked cases gives good agreement.

3. Found error in the values of characteristics roots for v shape and rectangular shape cracked cases is slightly more when crack depth increases above 50 mm.

4. When the depth of the second crack is kept constant and second crack location is varied from the cantilever end of the beam, then characteristics root of the beam increases.

5. In case of 2 cracks of different depths, the larger crack is comparatively more responsible for reducing the value of natural frequency.

6. When the location of the second crack is kept constant and crack depth increases then characteristics root of the beam decreases.

7. Characteristics root of the beam decreases significantly, when second crack location is nearer to the first crack location and when both the crack location closer to the cantilever end.

8. When the depth of the first crack increases, then value of characteristics roots decreases rapidly.