Beam elements as approximate models of vibrating mechanical subsystems of freight wagons

1. Introduction

The problems concerned with mechatronic systems and problems of electrostriction and piezoelectricity were presented for example in [8-10]. Other, diverse problems have been modelled by different methods [1, 2] and next they were examined and analyzed in (e.g. [3-7]).

2. The algorithm of the exact method for obtaining the solution of transverse vibrating free beam – simple subsystem of complex beam system

In the global case the equation of motion of the beam is considered:

where: $y(x,t)$ is deflection at the time moment $t$ of the lining beam section within the distance x from the beginning of the system, $E$ – Young modulus, $\rho$ – mass density of material of the beam, $I$ – polar inertia moment of the beam cross section, $F$ – area of the beam cross section.

The boundary conditions of beam system are known as: free ($F$), clamped ($C$), pinned ($P$) and sliding ($S$) ends.

The solution of Eq. (1) is the function in form of:

After transformations own functions are obtained as:

The problem of determining of own function was presented for discrete-continuous transverse vibrating mechatronic systems in (e.g. [8-10]).

3. The algorithm of the exact method for obtaining the dynamical flexibility of transverse vibrating beam – subsystem of freight wagons

Taking into consideration that mechanical subsystem of transverse vibrating complex system is extorted with harmonic force in form $P\left(t\right)=P_0\mathrm{s}\mathrm{i}\mathrm{n}\omega t$, so one boundary condition in combination $F$, $C$, $P$, $S$ Eq. (1) takes form:

After substituting of derivatives and transformation the deflection of the beam is considered as:

According to definition of dynamic flexibility it takes form:

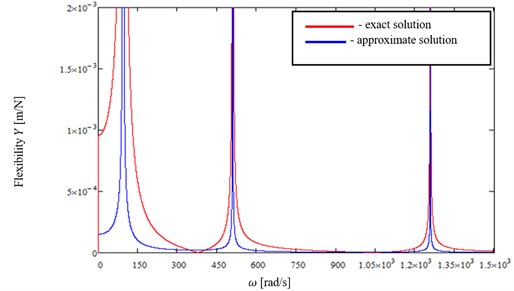
The graphs of absolute value of dynamical flexibility Eq. (6), obtained for $x=l$, for combinations of boundary conditions: free end – ($F$) and pinned end – ($P$) are presented in Fig. 1 and for clamped end – ($C$) and sliding end – ($S$) – in Fig. 2.

Detailed transformations and final sentences of combinations of boundary conditions have been presented in (E.g. [8-10]).

4. The algorithm of approximate method for obtaining the dynamical flexibility of transverse vibrating beam - subsystem of freight wagons

It has to be considered that if the beam is under the action of moment with continuous factorization threw the beam length with the value $F\left(x\right)\mathrm{s}\mathrm{i}\mathrm{n}\omega t$on the length unit – then the equation of motion of the element with length $d_x$ lining in the point $x$ is:

where: $P_0=F/h$.

Using approximate method – Galerkin’s one, the solution of Eq. (7), after transformations is given in the form:

After transformation, the equation of dynamical flexibility is:

In general case the dynamical flexibility at the arbitrary point of the beam after transformations gets a form of:

Plots of absolute values of dynamical flexibility defined by Eq. (10) for combinations of boundary conditions ($C$)-($S$) and ($F$)-($P$) are presented in Fig. 1 and 2.

Fig. 1Absolute values of dynamical flexibility of the beam with combination of boundary conditions (F) and (P), for n= 1, 2, 3

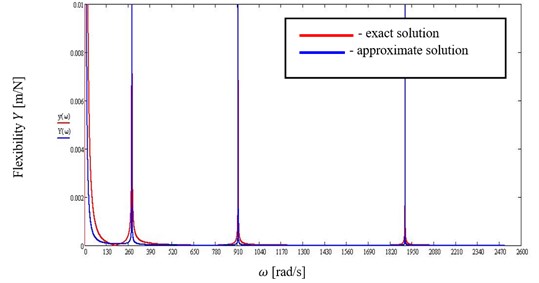
Fig. 2Absolute values of dynamical flexibility of the beam with combination of boundary conditions (C) and (S), for n= 1, 2, 3

5. Conclusion

The problems presented in this paper are considered to be the base and introduction to the solution of inverse task, meaning the synthesis of transverse vibrating complex mechanical or mechatronic beam systems with assumed frequency spectrum.