Piecewise constant control of a precise measurement platform

1. Introduction

Control of a precise measurement platform is investigated. Model having one degree of freedom is used. Control procedure on the basis of finite element in time and the method of least squares is proposed. Piecewise constant control force is obtained. The proposed method of control is based on the material presented in [1-5]. Related problems are investigated in [6-11]. On the basis of performed investigations for various values of parameters the necessity to follow not only the desirable displacement, but also the desirable velocity is shown.

2. Control of a precise measurement platform

Motion of a precise measurement platform is approximated by the standard one-dimensional differential equation:

where $m$ is the mass of the platform, $u$ is the displacement, $c$ is the coefficient of viscous damping, $k$ is the coefficient of stiffness, $f$ is the external force, upper dot denotes differentiation with respect to time.

Linear interpolation of displacements on the basis of the method of finite elements yields:

where $T$ is the time step, the subscript 0 corresponds to the value at the beginning of the time step, the subscript $T$ corresponds to the value at the end of the time step. Calculations of displacements by using this finite element are based on the following equation:

where:

Calculations of velocity by using this finite element are based on the following equation:

The following equation for displacement is obtained:

where:

The following equation for velocity is obtained:

where:

The following error function is introduced:

where ${\lambda }_1$ and ${\lambda }_2$ are the weighing parameters, $\stackrel{-}{u}$ is the desirable displacement, $\stackrel{-}{\dot{u}}$ is the desirable velocity.

This function can be rewritten as:

By minimizing the error, it is obtained:

Thus, the excitation is calculated as:

3. Computational experiments for the control of a precise measurement platform

The following parameters of the investigated precise measurement platform are assumed: $m=$ 1, $c=$ 0.1, $k=$ 1$.$

Desirable motion is assumed as:

where $\omega$ is the angular frequency of harmonic motion, $t$ is the time variable.

Initial conditions are assumed as:

Time step is assumed as:

Displacement control is performed by assuming ${\lambda }_1=\text{1}$ and ${\lambda }_2=\text{0.}$ Displacement and velocity control is performed by assuming ${\lambda }_1=\text{1}$ and ${\lambda }_2=$ 1.

Control of the precise measurement platform is investigated for various values of frequency of desirable motion. Typical results of control of the precise measurement platform when $\omega =\text{0.5}$ are presented in detail further.

3.1. Displacement control

Displacement control is performed by assuming ${\lambda }_1=\text{1}$ and ${\lambda }_2=$ 0.

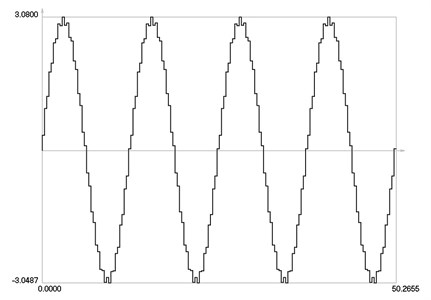
Variation of the control force is presented in Fig. 1.

Variations of displacement and velocity are presented in Fig. 2.

Fig. 1Control force as function of time

Phase trajectory of velocity as a function of displacement is presented in Fig. 3.

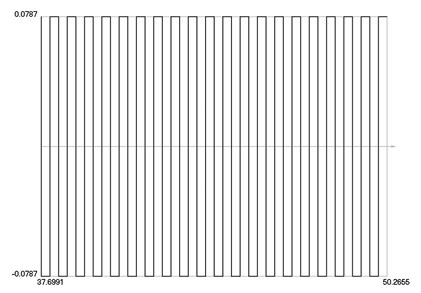
From the presented graphical representation, it is seen that the control force has undesirable high frequency oscillations. Thus, their investigation for one period of steady state motion is performed in more detail. Variation of the control force over one period of steady state motion is presented in Fig. 4.

By using the method of collocation – least squares the first harmonic of the control force over one period of steady state motion is determined. Midpoints of time steps are used as collocation points. The first harmonic of the control force over one period of steady state motion is presented in Fig. 5.

Fig. 2Displacement and velocity as functions of time

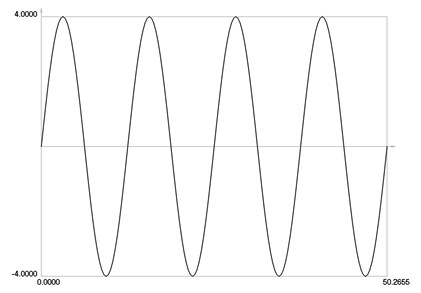
a) Displacement as function of time

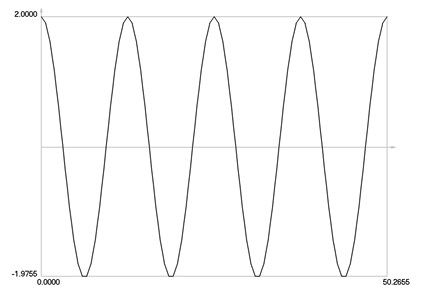
b) Velocity as function of time

Fig. 3Phase trajectory of velocity as a function of displacement

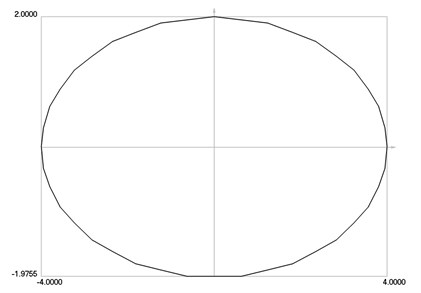
Fig. 4Control force as function of time over one period of steady state motion

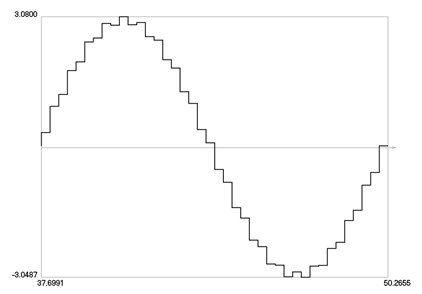
Fig. 5The first harmonic of the control force as function of time over one period of steady state motion

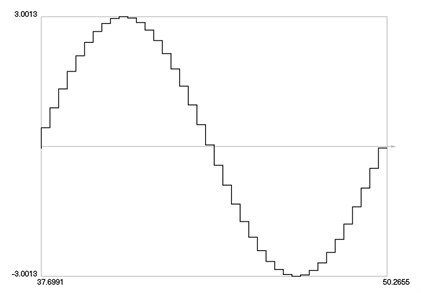
Fig. 6The error of the control force as function of time over one period of steady state motion

The error (that is deviation from the first harmonic) of the control force over one period of steady state motion is presented in Fig. 6.

From the presented results, it is seen that the variation of the control force is not acceptable and thus it cannot be recommended to perform only displacement control.

3.2. Displacement and velocity control

Computational experiments for the displacement and velocity control are performed by assuming ${\lambda }_1=\text{1}$ and ${\lambda }_2=$ 1. Variation of the control force is presented in Fig. 7.

Fig. 7Control force as function of time

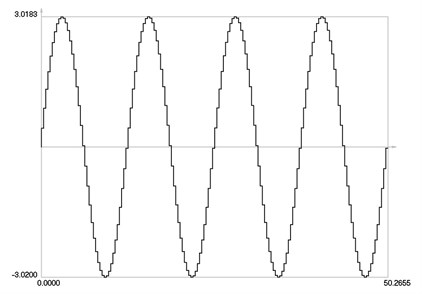
Fig. 8Displacement and velocity as functions of time

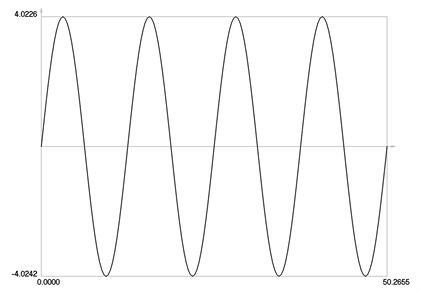
a) Displacement as function of time

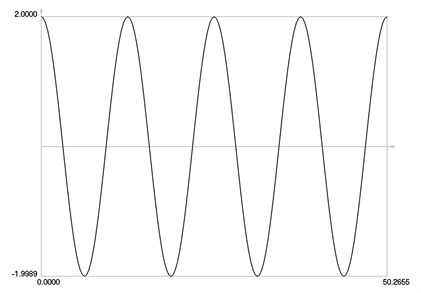
b) Velocity as function of time

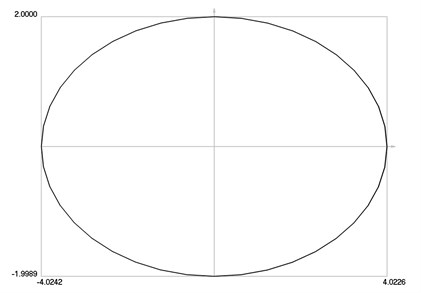
Fig. 9Phase trajectory of velocity as a function of displacement

Variations of displacement and velocity are presented in Fig. 8.

Phase trajectory of velocity as a function of displacement is presented in Fig. 9.

From the presented results, it is seen that the variation of the control force is acceptable (high frequency oscillations are not observed in the obtained results) and thus displacement and velocity control is recommended for engineering applications where the stabilization of harmonic oscillations is required.

4. Conclusions

Control of a precise measurement platform is investigated. Model having one degree of freedom is used. Control procedure on the basis of finite element in time and the method of least squares is proposed. Piecewise constant control is investigated.

From the presented results, it is seen that the resulting variations of displacement and velocity as functions of time are acceptable for both problems: problem of displacement control and problem of control of both displacement and velocity. But piecewise constant variation of the control force has high frequency vibrations when only displacement control is performed. Computational simulations demonstrate the necessity to follow not only the desirable displacement, but also the desirable velocity of the controlled system. Experimental implementation of the proposed technique is a definite objective of future research.