Improving the weak feature extraction by adaptive stochastic resonance in cascaded piecewise-linear system and its application in bearing fault detection

1. Introduction

Rolling element bearing is one of the most common mechanical components and plays a vital role in rotating machineries. They are highly liable to malfunction such as the inner ring, outer ring, the rolling elements and the cage since the rolling bearings usually operate under a harsh working environment [1, 2]. Therefore, machinery performance may suffer serious deterioration and even there are heavy casualties and property losses without the health monitoring and timely fault diagnosis of rolling bearings [3]. Owing to the inherent relationship between bearings operation and vibration, vibration signals collected from bearings are rich in information about bearings performance. Thus, using vibration signals to detect bearing fault has been extensively researched during the past decades [4, 5]. However, early fault features are far weak and submerged in heavy noise, so it is quite challenging to effectively extract them. Traditionally, in order to obtain the fault features, various signal processing techniques, such as wavelet transform [6, 7], local mean decomposition [8-10], empirical mode decomposition [11-14], etc., aim at eliminating and suppressing the noise because it is always considered an undesirable disturbance contaminating the useful signals. Although these traditional denoising methods exhibit an excellent effect, the useful signal components may inevitably be weakened or even destroyed during this process resulting in not effectively extracting the fault features.

Different from traditional denoising methods, stochastic resonance (SR) is an effective method which can extract the weak features by utilizing noise instead of removing noise. Since SR theory was proposed by Benzi et al. [15], it has been extensively applied in signal processing. For SR can transfer noise energy to the weak features, weak features are enhanced while noise is decreased. As a result, weak features submerged in heavy noise are successfully extracted. In recent years, SR has become an advanced research hotspot in the field of weak feature extraction due to its advantage of utilizing noise to enhance the weak features. Consequently, there are more and more research achievements based on SR in weak feature extraction. Moreover, it is proved that the SR method possesses a good prospect of engineering applications by analyzing the data in real industrial engineering situations. For example, Li et al. [16] applied the adaptive monostable SR method to process the engineering signal from the worm of a horizontal boring and milling machine in a factory, and the results show that the SR method can raise the signal-to-noise ratio (SNR) and the worm faults can be diagnosed effectively. Lei et al. [17] proposed a new adaptive SR method and used it to analyze a real case of locomotive rolling element bearings with an early fault, and the results show the weak features are detected effectively, thus the early faults are diagnosed accurately. Qiao et al. [18] applied adaptive unsaturated bistable SR method into fault characteristic extraction of a real locomotive rolling element bearing with the flaking fault on the outer race, and ultimately the extraction results demonstrated that the SR method is quite good at detecting the weak fault characteristics submerged in heavy noise in the industrial environment. These current studies indicate that the weak features can be well enhanced and extracted through a single SR to some extent. However, the performance of the single SR for the weak feature extraction is usually finite. For instance, we can’t discover the fault features after using a single SR when the SNR is very low, such as the bearing fault signals in which the fault features are submerged in badly heavy background noise. Therefore, the weak features can’t be efficiently extracted by a single SR for bearing fault signals.

In order to settle the problems mentioned above, namely, further improving the weak feature extraction performance, some works based on cascaded SR [19-25] have done until now. As a result, the weak feature extraction performance of cascaded SR has evident improvement compared with that of the single SR. However, the present study on cascaded SR has mostly paid attention to the bistable system; only a few literatures on other systems can be found. Wang et al. [26] demonstrated that the piecewise-linear SR has better extraction performance for the weak periodic signals in heavy noise compared with the classical bistable SR. Thus, in this paper, a method based on the cascaded piecewise-linear SR is presented. At the same time, in order to sufficiently show the advantages of piecewise-linear SR model in the weak feature extraction, this paper will adopt a more efficient algorithm called quantum particle swarm optimization proposed by Sun et al. [27] to optimize system parameters. In addition, due to the limitation of the adiabatic approximation theory, the input signals are preprocessed by the scale transformation theory [28, 29], which is used for processing signals with high frequency. We call the method proposed in this paper as adaptive cascaded piecewise-linear SR. Simulation and experimental results show our method can effectively realize weak signal detection and early fault diagnosis.

The present paper is arranged as follows. Section 2 introduces the theory of the piecewise-linear SR. Then, cascaded SR based on the piecewise-linear model is described. In Section 3, the cascaded SR is realized by two different procedures, i.e. keeping every order system parameters invariable and optimizing every order system parameters with the best, which are simply introduced and compared by numerical simulations. According to the comparison and analysis results, a high-performance weak feature extraction method is proposed. In Section 4, the proposed method is used to process the bearing fault experimental signals to verify the high-performance and robustness of this method in the weak fault feature extraction. Finally, the main results of this paper are concluded in Section 5.

2. Cascaded piecewise-linear SR

2.1. Theory of the piecewise-linear SR

For the piecewise-linear model, $U\left(x\right)$ represents a potential function as follows:

1

$U\left(x\right)=\left\{\begin{array}{l}-\frac{c}{a-b}\left(x+a\right),x<-b,\\ \frac{c}{b}x,-b\le x<0,\\ -\frac{c}{b}x,0\le x<b,\\ \frac{c}{a-b}\left(x-a\right),b\le x,\end{array}\right.$

where $a$, $b$ and $c$ denote the system parameters and $a>b>0$, $c>0$.

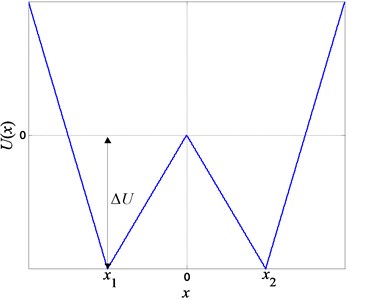
The potential described by Eq. (1) has two stable states $x_{\mathrm{1,2}}=\pm b$ and one unstable state $x_0=\text{0}$. The height of the potential barrier is $∆U=c$. In Fig. 1 we draw the curve of $U\left(x\right)$. Compared with the bistable model, parameters of the piecewise-linear model are highly less correlative and much easier to adjust. For instance, in the piecewise-linear model we can easily alter the position of the potential well by only adjusting parameter $b$, meanwhile keeping the height of the potential barrier. Or we can easily alter the height of the potential barrier by only adjusting parameter $c$, meanwhile keeping the position of the potential well.

Here the Langevin equation of the piecewise-linear model can be written as:

2

$\frac{dx}{dt}=-\frac{dU\left(x\right)}{dx}+s\left(t\right)+n\left(t\right)=\left\{\begin{array}{l}\frac{c}{a-b}+s\left(t\right)+n\left(t\right),x<b,\\ -\frac{c}{b}+s\left(t\right)+n\left(t\right),-b\le x<0,\\ \frac{c}{b}+s\left(t\right)+n\left(t\right),0\le x<b,\\ -\frac{c}{a-b}+s\left(t\right)+n\left(t\right),b\le x,\end{array}\right.$

where $x$ represents the displacement of a Brownian particle, $s\left(t\right)$ is the input signal, and $n\left(t\right)$ denotes the noise item with $n\left(t\right)=\sqrt{2D}\xi \left(t\right)$ and $〈n\left(t\right)n\left(t\text{'}\right)〉=2D\delta (t-t\text{'})$, in which $D$ is the noise intensity, $\delta \left(t\right)$ represents a Gaussian white noise with zero mean and unit variance and $〈*〉$ stands for statistical mean.

Fig. 1Curve of the potential function Ux for the piecewise-linear model

As already described in the ‘Introduction’ section, SR is a phenomenon where signal weak features can be enhanced while noise is decreased. Generally, the three basic ingredients of the piecewise-linear SR system are shown in Fig. 2 including a weak input signal $s\left(t\right)$, a source of noise $n\left(t\right)$ and a piecewise-linear system $U\left(x\right)$. Here, if these basic ingredients can match well, the Brownian particle can cross the potential barrier and enter another potential well from the former potential well. Meanwhile, the Brownian particle can continuously cross the potential barrier from one potential well to another one by modulation frequency of the input signal, resulting in synchronization between the output and the input signal. This indicates SR phenomenon happens. As a consequence, the signal weak features are enhanced and the output signal has a higher SNR by contrast with the input signal. Hence the detection of weak features submerged in heavy noise is probable.

Fig. 2Framework of single piecewise-linear system

2.2. Cascaded piecewise-linear SR

As Fig. 3 shows, through series connection, the single piecewise-linear system becomes cascaded piecewise-linear system. Thus, the Langevin equation of cascaded SR system can be expressed as:

3

$\begin{array}{l}\frac{d{x}_1}{dt}+\frac{d{U}_1\left(x_1\right)}{dt}=s\left(t\right)+n\left(t\right),\\ \frac{d{x}_i}{dt}+\frac{d{U}_i\left(x_i\right)}{dt}=x_{i-1}\left(t\right),i=\mathrm{2,3},...,P.\end{array}$

In Eq. (3), $s\left(t\right)$ and $n\left(t\right)$ are the input of cascaded system and $P$ is the number of the single system cascaded system contains. In addition, $x_i\left(t\right)$ is the output of the $i$th order cascaded system, but also the input of the next order cascaded system.

Fig. 3Framework of cascaded piecewise-linear system

In cascaded systems, through this kind of connection, multiple single systems are organically linked. In terms of single SR, after the original signal is input into SR system, the output spectrum energy is focused on the low-frequency region, and the corresponding high-frequency energy is reduced. However, by this form of cascading, the high-frequency energy is continually transferred to the low-frequency region to some extent, so a better SR phenomenon presenting. Finally, the energy of the characteristic frequency is further strengthened, and the weak features are effectively extracted.

3. Numerical simulation

Among the methods of extracting signal weak features, SR has been proved effective to some extent. To further improve the weak feature extraction performance, an enhanced method called cascaded SR has been investigated. So far, a few of achievements about cascaded SR have been published in academic journals and conference proceedings. However, the investigation on cascaded SR at present is principally concentrated in keeping every order system parameters invariable to produce SR. Although the weak feature extraction performance has evident improvement via this type of methods, there are still some scopes for more improvement if every order system parameters are optimized with the best. In this paper, the two enhancement methods, i.e. keeping every order system parameters invariable and optimizing every order system parameters with the best to investigate cascaded piecewise-linear system output, are compared.

Considering our investigation aims at bearing fault diagnosis, this paper adopts one kind of periodical impulse signal to simulate bearing vibration. The simulation fault signal is generated by the follow equation [30]:

where $A$ is the signal amplitude, $f_0$ is the carrier frequency, $d$ denotes the attenuation index, $f_d$ is the fault frequency, and $m\left(t\right)=$ floor [$t{f}_d$] controls the impulse periodicity where “floor” is the integral function.

Traditional SR is only suitable for processing signals with low frequency due to the limitation of the adiabatic approximation theory [31-33]. However, the characteristic frequency of the simulation bearing fault signal for this paper obviously cannot meet the condition to produce SR phenomenon. Thus, the input signal is first preprocessed by the scale transformation theory, which is used for processing signals with high frequency. Moreover, in order to make piecewise-linear system achieve SR, system parameters need to be adjusted. If various parameters of the system are simultaneously optimized to find global optimal solution, the best SR phenomenon may happen. Due to its fast convergence speed, fortissimo global optimization ability and high search precision, quantum particle swarm algorithm has shown a wonderful performance in signal processing. Therefore, in this paper, parameter $a$ and $c$ in Eq. (2) are simultaneously optimized by quantum particle swarm algorithm. Above process is called the adaptive SR (ASR). The SNR which is defined by Eq. (5) [34] is chosen as the evaluation index for the ASR performance. When the output SNR reaches the maximum, the ASR system can produce the optimal output. The flowchart of the ASR is shown in Fig. 4:

where $f$ is the characteristic frequency and $k$ is, the serial number corresponding to $f$, $S\left(f\right)$ is the amplitude at $f$ and $N\left(f\right)$ denotes the average amplitude of the background noise near $f$ in the power spectrum, $X\left(k\right)$ is the amplitude at $f$ in the frequency spectrum, and $M$ is selected according to the date length $N$ and the sampling frequency $f_s$.

Initially, we keep every order system parameters ($a$ and $c$) invariable to excite SR phenomenon. We firstly optimize the parameters of the first order cascaded piecewise-linear system with the best by quantum particle swarm algorithm to excite SR phenomenon, and then utilize the optimization results of the first order cascaded system parameters driving the second order system to produce SR, etc. In the simulation, $A=$ 1, $d=$ 15000, $f_0=$ 2062 Hz and $f_d=$ 103 Hz. In addition, the sampling frequency $f_s$ and the date length $N$ are respectively set to 10000 Hz and 10000. Fig. 5(a) shows the time-domain waveform and the frequency spectrum of the pure simulation signal. A Gaussian white noise with the intensity $D=$ 0.5 is added to the pure simulation signal, and the noisy simulation signal with corresponding frequency spectrum is shown in Fig. 5(b). Obviously, the peak of the characteristic frequency is totally submerged in the background noise and it is difficult to identify it. Hence, the envelope analysis by the Hilbert transform is implemented to extract the frequency of the noisy signal. As shown in Fig. 5(c), it indicates that the characteristic frequency can be revealed slightly after the envelop demodulation. In order to eliminate the interference of the low frequency components and find the characteristic frequency clearly, the envelop signal is processed through high-pass filter where the cutoff frequency is 100 Hz, and the result is shown in Fig. 5(d). Then cascade piecewise-linear SR system in which cascaded number $P$ is set to 9 is used to process the simulation signal in Fig. 5(d), and the output frequency spectrums are presented in Fig. 6. We can distinctly see the peak of the characteristic frequency by the first order cascaded piecewise-linear system in Fig. 6(a). Meanwhile, the output SNR of the first order cascaded system is calculated and shown in the top right corner in Fig. 6(a). The output SNR of the first order cascaded system has an advance of 2.76 dB as compared to the input filtered signal. However, starting from the second order system, the system will be divergent, and the peak of characteristic frequency cannot be revealed due to the energy mechanism of the SR system from high-frequency region to low-frequency region. In the end, we fail to extract the characteristic signal. Obviously, we cannot achieve the desired effect to further improve the weak feature extraction performance by this procedure. In general, the output spectrum distribution is different after every order system, so applying the first order cascaded system parameters which are optimized to the next order cascaded system is unavailable to make cascaded system produce the optimal output.

Fig. 4Flowchart of the ASR based on the quantum particle swarm algorithm. The contraction-expansion coefficient β is calculated according to the probability principle about quantum computation

Fig. 5Time-domain waveforms and frequency spectrums of the simulation signal: a) pure signal; b) noisy signal; c) envelope signal; d) filtered signal

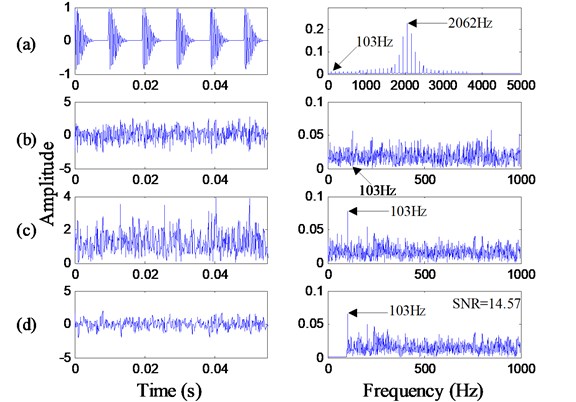
Fig. 6Output results of cascaded piecewise-linear SR system based on keeping every order cascaded system parameters invariable: a) to i) are the output frequency spectrums of the first to ninth order cascaded system, respectively

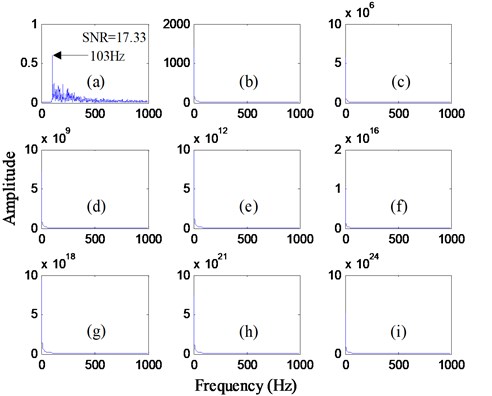
Now, we try to optimize the parameters ($a$ and $c$) of every order cascaded piecewise-linear system with the best by quantum particle swarm algorithm, and then explore whether cascaded system can produce the optimal output. Consequently, the output frequency spectrums of the first to ninth order cascaded system are presented in Fig. 7 where the output SNR of every order cascaded system after calculated is shown in the top right corner accordingly. Observing the frequency spectrum of every order cascaded system, the peak of the characteristic frequency is more and more distinct in the whole spectra with the increase of cascaded order, and ultimately it is extremely easy to identify it. Moreover, with the increase of the order in cascaded system, the corresponding output SNR gradually increases as well. The output SNR of the first order only has an advance of 2.76 dB as compared to the input filtered signal, but this index is stupendously increased by 5.68 dB at the ninth order, which implies it is possible to extract the signal weak features with far low SNR by this procedure.

Fig. 7Output results of cascaded piecewise-linear SR system based on optimizing every order parameters with the best: a) to i) are the output frequency spectrums of the first to ninth order cascaded system, respectively

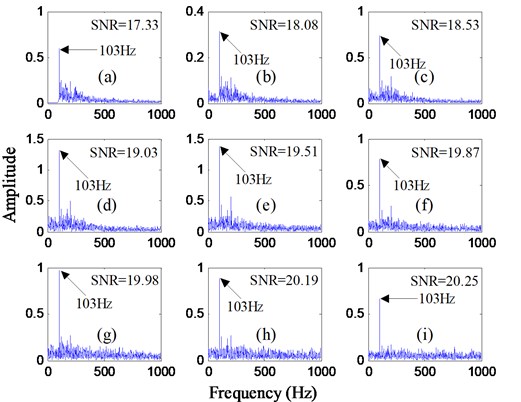
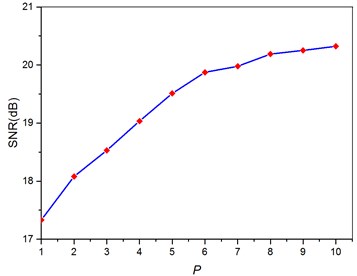
Obviously, using this procedure, we can achieve the desired effect to further improve the weak feature extraction performance. On the other hand, in order to specifically describe this increase about the output SNR, the curve denoting the relationship between cascaded order and the corresponding output SNR is depicted in Fig. 8 where the output SNR will increase rapidly with the increase of cascaded order when cascaded order is relatively less, then slowly increase with the continued increase of the cascaded order and rarely increase afterwards. This rule can be explained in terms of cascaded piecewise-linear system impact on the noise distribution. In Eq. (3), Gaussian white noise is input into the first order cascaded system, and then the output is the colored noise in the form of Lorentz, which means the high-frequency components of the noise is transferred to the low-frequency signal that is strengthened to achieve SR eventually. After the next order cascaded system, the colored noise in the form Lorentz continues to transfer its high-frequency components to the low-frequency signal, so that the output SNR has growing enhancement with the increase of the order in the cascaded system. Until after a higher order in the cascaded system, the signal has been very little high-frequency components, thus the high-frequency energy is rarely transferred to low-frequency region with the increase of cascaded order. In consequence, the output SNR also will no longer advance.

Through the simulation results for the periodical impulse signal, we find that we fail to extract the weak features from heavy noise if every order cascaded system parameters are kept invariable. On the contrary, cascaded system where every order system parameters are optimized with the best can achieve higher output SNR, thus the weak feature extraction performance is further improved. Thereby, a high-performance weak feature extraction method called adaptive cascaded piecewise-linear SR (ACPLSR) is proposed for fault diagnosis of rolling bearings, and the flowchart of this method is shown in Fig. 9.

As the results shown above, selecting the excessive cascaded orders is a technical problem. On the one hand, it is not easy to achieve when cascaded order is excessive in practical application. In addition, through analyzing the results in Fig. 8, the relationship between the output SNR and the cascaded order is not proportional, and namely cascaded order is not the larger the better. So, it is particularly important to select a suitable value for cascaded order $P$. According to the rule obtained in Fig. 8, we generally set a fixed $P$, e.g. 4 or 5.

Fig. 8Relationship between the order and the corresponding output SNR in the cascaded piecewise – linear system based on optimizing every order parameters with the best

4. Experimental verification

To verify the high-performance and robustness of the proposed method in practical application, sets of experimental dates from the bearing vibration signals are analyzed using the ACPLSR method. The experimental data are from the bearing data center website of the Case Western Reserve University (CWRU) [35], and the associated test rig is shown in Fig. 10. The experimental system includes a 2 hp motor, a torque transducer/encoder, dynamometer and control electronics.

Fig. 9Flowchart of the proposed method for fault diagnosis of rolling bearings

Fig. 10Rolling bearing fault simulation test rig from CWRU

The bearing vibration signals are collected using accelerometers which are mounted on the motor housing with magnetic bases in 12 o’clock position under different motor speeds, and the sampling frequency is 12000 Hz. In this paper, the date used to analyze come from the drive-end bearing outer ring fault with fault diameter of 0.007 inches. The drive end bearing is deep groove ball bearing of the type 6205-2RS JEM SKF, and the parameters is listed in Table 1. The characteristic frequency of the bearing outer ring fault can be calculated by the following equation:

where $\tau$ is the motor speed, $z$ is the ball number, $\alpha$ is the contact angle, and $d$ and $D_m$ are the ball and pitch diameters, respectively. Thus, the defect frequencies of outer ring are calculated and listed in Table 2 under different motor speeds.

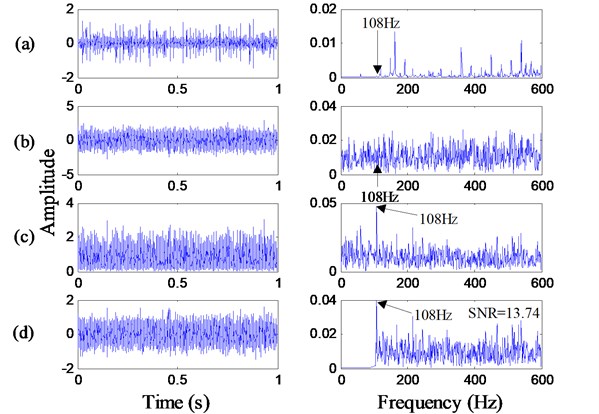
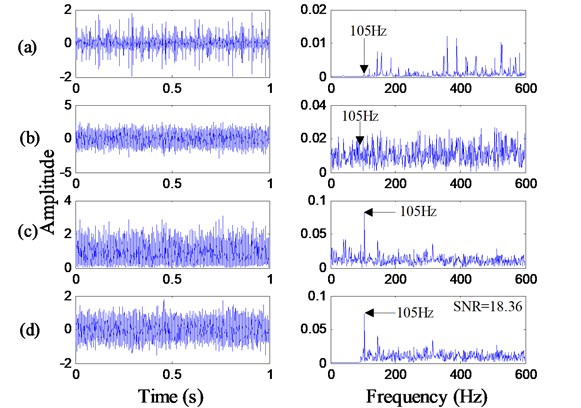
Fig. 11(a) shows the time-domain waveform and the frequency spectrum of the original signal from the bearing outer ring fault with the motor speed 1797 rpm. We can find the obvious periodic impulses in the time-domain waveform, and the defect frequency can hardly be seen in the frequency spectrum due to the heavy noise interference. Thus, we use the proposed method shown in Fig. 9 to detect weak fault features. Firstly, a Gaussian white noise with intensity $D=\text{0.2}$ is added to the original signal, and the noisy signal with corresponding frequency spectrum is shown in Fig. 11(b). Then, the noisy signal is preprocessed by the Hilbert transform and high-pass filter where the cutoff frequency is 105 Hz. As a result, the envelope signal and filtered signal of the bearing outer fault are shown in Fig. 11(c) and Fig. 11(d), respectively. In the frequency spectrum, whether the envelope signal or filtered signal, the defect frequency 108 Hz can be perceived slightly. However, the peak of the defect frequency is weak and there is still heavy noise. Moreover, the SNR of the filtered signal is calculated, and its value is 13.74 dB shown in the top right corner of Fig. 11(d).

Fig. 11Time-domain waveforms and frequency spectrums of the bearing outer ring fault signal with the motor speed 1797 rpm: a) original signal; b) noisy signal; c) envelope signal; d) filtered signal

Subsequently, the preprocessed signal is input to the ACPLSR system where cascaded order $P$ is set to 4 according to the analysis results in Section 3. Consequently, the output frequency spectrums of the first to fourth order cascaded system are presented in Fig. 12 where the output SNR of every order cascaded system is calculated and shown in the top right corner. Observing the output frequency spectrum, the peak of the defect frequency is more and more distinct in the whole spectra with the increase of the order in ACPLSR system, and ultimately it is extremely easy to identify it. The reason for above results is that the output SNR is gradually enhanced with the increase of cascaded order. Observing the value of the output SNR in the first to fourth order ACPLSR system, the output SNR of the first order only has an advance of 2.58 dB as compared to the input filtered signal, but this index is further increased by 5.46 dB at the fourth order. We all know, to a certain extent, the higher the output SNR is, the better the weak feature extraction performance is. Thus, compared with the single SR system, this type of ACPLSR system has a far great significance for the improvement of the weak feature extraction performance. In the end, it can be included that the weak fault features are extracted effectively and the fault is effectively detected by the proposed method.

Fig. 12Frequency spectrums after analyzed by the proposed method for the bearing outer ring fault signal with the motor speed 1797 rpm: a) and d) are the output frequency spectrums of the first to fourth order ACPLSR system, respectively

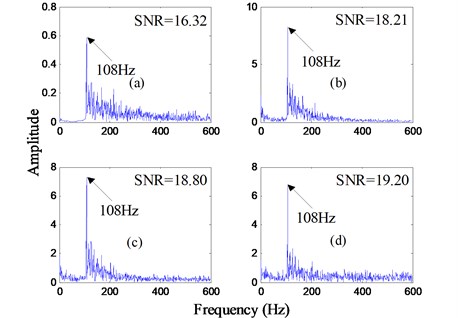
Fig. 13Time-domain waveforms and frequency spectrums of the bearing outer ring fault signal with the motor speed 1750 rpm: a) original signal; b) noisy signal; c) envelope signal; d) filtered signal

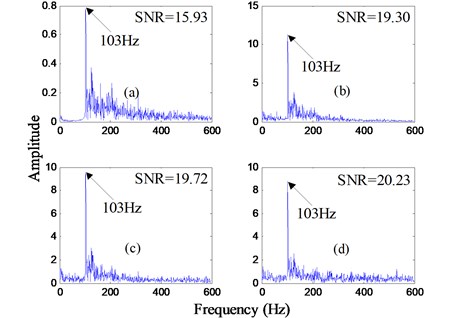
To verify the robustness of the ACPLSR method proposed in this paper, the data from the bearing outer ring fault signals with the motor speed 1750 rpm and 1724 rpm are analyzed using this method. Fig. 13 and Fig. 15 separately show the bearing outer ring signals. The analysis results based on the proposed method are shown in Fig. 14 and Fig. 16 separately. In Fig. 14, the output SNR of the first order only has an advance of 2.54 dB as compared to the input filtered signal, but this index is increased by 4.17 dB at the fourth order. In Fig. 16, the output SNR of the first order only has an advance of 2.86 dB as compared to the input filtered signal, but this index is increased by 7.16 dB at the fourth order. Obviously, compared with the single system, this ACPLSR method can further advance the output SNR or the weak feature extraction performance. Thus, it can be concluded that the proposed ACPLSR method can extract the weak fault features effectively under different motor loads, namely, that the robustness based on the proposed ACPLSR method is verified.

Fig. 14Frequency spectrums after analyzed by the proposed method for the bearing outer ring fault signal with the motor speed 1750 rpm: a) and d) are the output frequency spectrums of the first to fourth order ACPLSR system, respectively

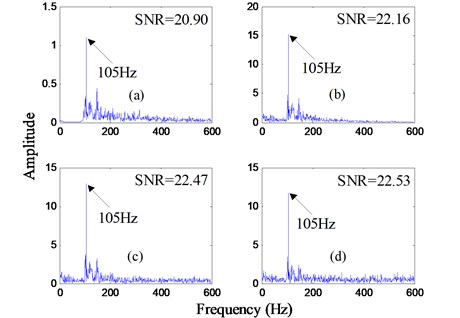
Fig. 15Time-domain waveforms and frequency spectrums of the bearing outer ring fault signal with the motor speed 1724 rpm: a) original signal; b) noisy signal; c) envelope signal; d) filtered signal

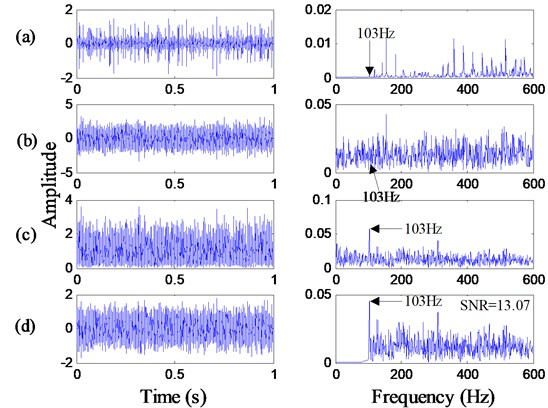
Fig. 16Frequency spectrums after analyzed by the proposed method for the bearing outer ring fault signal with the motor speed 1724 rpm: a) and d) are the output frequency spectrums of the first to fourth order ACPLSR system, respectively

5. Conclusions

To realize the health monitoring and timely fault diagnosis of rolling element bearings, effective extraction of the weak fault features from heavy noise is urgently needed. In this paper, an effective adaptive cascaded SR method is proposed for the weak feature extraction in the bearing fault diagnosis. The SR model that the proposed method is based on is piecewise-linear system which has higher performance or output SNR than traditional bistable system. Moreover, the system parameter $a$ and $c$ in every single system are simultaneously optimized with the best by quantum particle swarm algorithm, leading to that cascaded system achieves the optimal output.

The proposed method is used to analyze the simulation impulse signal and the bearing experimental data. The analysis results indicate the system output SNR is greatly enhanced by this method, namely, that the weak feature extraction performance can be further improved in rolling element bearing fault diagnosis.