Abstract
For detecting the weak fault diagnosis submerged in heavy noise, a new method called multi-scale cascaded multi-stable stochastic resonance (MCMSR) is studied. The method can effectively extract weak fault diagnosis from noise background using multi-scale wavelet noise tuning stochastic resonance (SR). Firstly, input signal with noise is decomposed by multi-scale wavelets transformation, and each scale signal is adjusted by scaling factor, then the decomposed signal is used as the input of cascaded multi-stable systems to achieve the detection of fault diagnosis. If the input signal is a large parameter signal, to conform to the conditions of SR, the decomposed signal must be processed by twice sampling. The simulation and experimental signals are carried out to test the feasibility of the method. From the signal to noise ratio (SNR) comparison curves of original signal, SR output signal and MCMSR output signal plotted together, we can find that the useful signal can be enhanced by MCMSR method than SR method. The experimental results indicate that the MCMSR can extract fault diagnosis from heavy background noise.
1. Introduction
Signal feature extraction method has been widely used in many fields such as radar, seismic survey, oil well logging, satellite communications and so on. In most cases, the useful signal is submerged in heavy noise, which increases the difficulty to identify useful signal features. A lot of traditional signal detection methods are used to detect weak signal, e.g. the matched filtering, the adaptive filtering, the wavelet de-noising, the empirical mode decomposition (EMD) and so on [1-6]. These methods obtained the useful signal feature by suppressing or removing noise signal, but the disadvantages are that the useful signal may be weakened or even destroyed. Comparing with traditional methods, the stochastic resonance (SR) uses the noise instead of suppressing noise to extract signal feature. The SR method is proposed by scholar Benzi et al. in 1981 [7]. Thereafter SR method has received extensive attention, and shows a unique advantage in the aspect of weak signal feature extraction. SR system is consisted of nonlinear system, input signal and noise. SR phenomenon makes the energy transforms from noise to input signal and plays an important role in noise reduction of the signal [8].
In recent years, signal feature extraction method by SR theory has been developed rapidly [9-16]. Lu et al. [9] proposed a weak signal detection strategy for rolling element bearing fault diagnosis, which investigated a new mechanism to realize SR based on the Woods-Saxon (WS) potential. Moreover, an underdamped step-varying second-order SR (USSSR) method was proposed to further improve the output signal to noise ratio SNR [10]. A quantitative evaluation system on the performance and feature enhancement of SR was proposed to evaluate the feature enhancement effect of SR [11]. In ref. [12], the SR phenomenon of the bistable Duffing oscillator and its application on incipient fault diagnosis were investigated. He and Wang et al. [13-15] investigated improved SR approaches for identifying the defect-induced rotating machine faults and the identification of multiple transient faults in rolling element bearing, and presented an adaptive multiscale noise tuning SR (AMSTSR) for effective and efficient fault identification of rolling element bearings. Shi et al. [16, 17] proposed a novel weak signal detection method based on SR tuning by multi-scale noise, and studied a SR and analytical mode decomposition-ensemble empirical mode decomposition (AMD-EEMD) method for fault diagnosis of rotating machinery.
Adaptive Stochastic Resonance (ASR) on mechanical fault diagnosis has also been extensively investigated in recent years [17-20]. Qin et al. [18] studied an adaptive and fast SR approach to weak mechanical fault feature extraction. Chen et al. [19] studied a method of weak fault feature information extraction of planetary gear based on Ensemble Empirical Mode Decomposition (EEMD) and ASR. Lei et al. [20] studied an ASR method to solve the problem of weak feature extraction in fault diagnosis of planetary gearboxes.
In the past, the majority SR models are monostable or bistable SR systems. Recently, multi-stable SR models to detect weak signal are studied [21-24]. When the background noise is heavy, the multi-stable SR model has better noise metastatic capacity than the bistable SR model [21, 22]. Although SR has a distinct advantage in the weak signal processing, when the SNR of vibration signals is low, the detection effect of single SR is not satisfactory [25]. To obtain higher SNR, the Cascaded Stochastic Resonance (CSR) was proposed to increase the output SNR [26-29].
This paper proposes a multi-scale decomposition method by cascaded multi-stable SR system and studies its application on the detection of fault diagnosis in heavy background noise. The rest is organized as follows. Section 2 provides a short introduction to the multi-stable SR model. Section 3 studies the multi-scale wavelet decomposition method. Section 4 describes multi-scale decomposition method based on cascaded multi-stable SR system and presents a simulation example result. Section 5 and Section 6 provide an application experiment and the conclusions respectively.
2. The principles of multi-stable SR model
The multi-stable SR model is composed of a multi-stable nonlinear system, periodic input signal and noise. The synergistic reaction will occur in the nonlinear system by stochastic resonance, which will lead to the noise energy transfer into useful signal. The Langevin equation can be written as [22]:
where is the output signal; is driving signal, in which is amplitude and is driving signal’s frequency; represents noise, in which is noise strength and is Gaussian white noise.
For the multi-stable potential model, represents a potential function shown as:
where , and are the multi-stable potential barrier parameters. The value of , and determine the potential function which belong to multi-stable, bistable or monostable system. In this paper, the potential function belongs to the multi-stable system [29].
The Eq. (1) can be written as:
The potential function is symmetrical and has three stable points (, and ) and two unstable points (, ) shown as:
Eq. (4) describes the Brownian motion of an overdamped particle. When there are no a periodic signal and noise, the particle stays in one of three potential wells in multi-stable system. When the noise and input signal are added, the particles will overcome potential base and move among the tristable states, and the stochastic resonance phenomenon occurs [29]. Fig. 1(a) shows that the multi-stable system with input signal and white noise generates output response . Fig. 1(b) is the potential function waveform of a nonlinear multi-stable system, in which the values of , , are 0.52, –0.3 and 0.03, respectively. It can be supposed that a small ball in three potential wells do transition reciprocating motion. The system will occur SR when the frequency of reciprocating motion is equal to the frequency of weak periodic signal.
Fig. 1Multi-stable nonlinear model

a) Structure diagram of multi-stable stochastic resonance
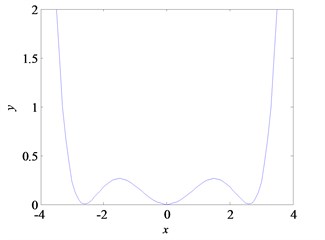
b) The potential function of multi-stable
3. Multi-scale wavelet decomposition
3.1. Discrete wavelet transform (DWT)
Wavelet transform has good localization ability, and can extract weak signal components from signal by multi-resolution decomposition [30].
A wavelet basic function is given as:
where is obtained by the dilation and translation of , is dilation factor and is frequency shift factor. Suppose , can be transformed into discrete wavelet by wavelet bases function . The wavelet transform coefficient is shown as:
where , and are continuous variables. Thus Eq. (9) is continuous wavelet transform.
Discrete wavelet function can be obtained by discreting the parameter of continuous wavelet function [31]. First, taking the correspond wavelet function is , . After taking , then the intervals of time axis is . Usually, discrete wavelet is binary discrete. When , and we can get , , where and . Then the correspond wavelet function is , where . Further is normalized, we can get the following function shown as:
Transform coefficient can be written as:
3.2. Multi-scale wavelet decomposition and reconstruction
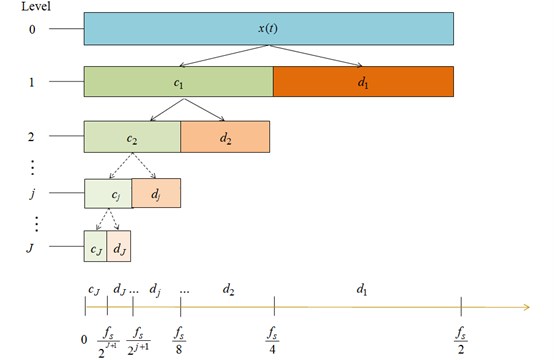
Binary orthogonal discrete wavelet transform decomposes signal into uncorrelated wavelet coefficients, and divides the wide band signal into a plurality of narrow bands. The schematic diagram of decomposition is shown in Fig. 2.
The decomposed wavelet coefficients include approximate coefficients and detail coefficients written in the form [32]:
where represents an inner product operator, is decomposition level, is cut-off decomposition level. The functions and are expressed respectively as:
where is the base functions of wavelet decomposition, is obtained by the dilation and translation of , is scaling function, is obtained by the dilation and translation of .
The inverse transform of DWT can be realized by the following function:
Adjusting the size of different scale signal’s amplitudes and reconstructing the signal, the signal can be expressed as:
where is scale contraction factor, and it can adjust amplitude of each scale component. In order to improve SNR, we usually turn the approximate coefficients of scale contraction factor to higher, while turn the detail coefficients of scale contraction factor to lower.
Fig. 2Using DWT to decompose the signal x(t)
4. Multi-scale cascaded multi-stable stochastic resonance system
4.1. Multi-scale multi-stable stochastic resonance method
Wavelet transform has good localization properties in time-frequency. The signal can be decomposed into different scale frequency components by multi-scale wavelet decomposition. Due to the strong selection characteristics of noise intensity and frequency in nonlinear multi-stable system, each scale signal need to be adjusted by scaling factor. Then the decomposed signal is used as the input of the cascaded multi-stable systems. When the signal is processed by multi-scale wavelet decomposition, the noise intensity of input signal is reduced after decomposition. The schematic of multi-scale cascaded multi-stable SR system is shown in Fig. 3.
Fig. 3The schematic of multi-scale SR system
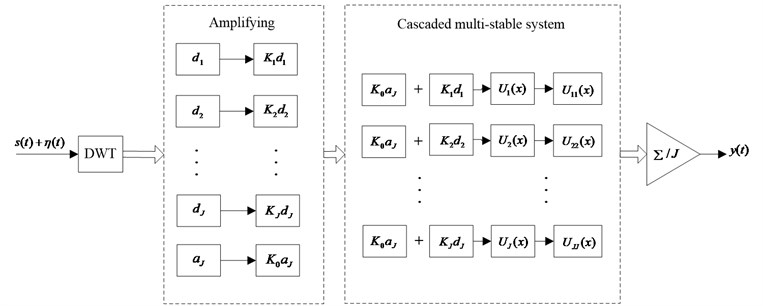
Firstly, the signal is reorganized by the approximate signal with each scale noise. The noise is equivalent to noise reduction signal. Then, it is used as the new input signal of each cascaded multi-stable system to optimize SR effect of each unit. And the output signal of entire system is the average value of output of all units [33]. In addition, we select the decomposition scale by the traversing method.
4.2. Multi-scale cascaded multi-stable SR system
We proposed a new SR system named multi-scale cascaded multi-stable SR system (MCMSR) shown in Fig. 4. The MCMSR model comprises a plurality of multi-stable SR systems. The output signal of first multi-stable system is used as the input signal of the second multi-stable system. The output signal of the second multi-stable system is used as the input signal of the third multi-stable system, and so on. At last, the output of the last level multi-stable SR system is the output of entire MCMSR model.
SNR is used to judge whether the system produces stochastic resonance. The calculation formula of SNR is written in the form:
where is the amplitude value corresponding to the driving signal frequency, and is the sum of all the amplitude values except in the amplitude spectrum [34].
Fig. 4Multi-scale cascaded multi-stable SR system

4.3. Simulation experimental verification
In order to conform to the adiabatic approximation theory, we select the small parameters signal. The input signal is . The amplitude of signal is equal to 0.3 and the frequency of signal is equal to 0.01 Hz. Let , in which is noisy signal, is Gaussian white noise and its strength is 0.6. The system parameters are , and , the value of each are 0.72, –0.3 and 0.08, respectively.
The waveform and spectrum of a noisy sinusoidal signal are shown in Fig. 5. Sampling frequency is 5 Hz. It can be observed in the frequency domain in Fig. 5, where there is a uniform distribution, and the white noise and frequency has a minor peak nearby 0.01 Hz, the amplitude is 0.3212.
Fig. 6(a) shows decomposition result of the processed signal after DWT. The db1 wavelet is used for decomposition and the scale is set to . The traversing method is used to select decomposition scale. The decomposition scale is set as 1, 2, 3, 4, 5, 6, and then the best decompose effect value of j is found. It can be seen from Fig. 6(a), is the original signal, is the signal’s low frequency part, to are the signal’s high frequency parts. Fig. 6(b) is spectrum after Fast Fourier Transform (FFT) of the original and the reconstructed signal of approximation signal and each scale noise signal. The size of each scale signal components of reconstructed signal is to be adjusted by the scale factor. From Fig. 6(b) we can find that there are distinct peaks at 0.01 Hz and the peak values in Fig. 6(bb) to Fig. 6(be) are much higher than that in Fig. 6(ba). In Fig. 6(be) there has the maximum peak value, but the peak value not exceeding 1. At the same time, there are many noise signal components in Fig. 6(bb) to Fig. 6(be). It shows that the result of wavelet decomposition is seriously affected by the noise.
Fig. 5The original signal’s waveform and spectrum
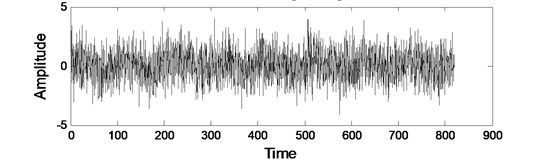
a) Waveform of original signal
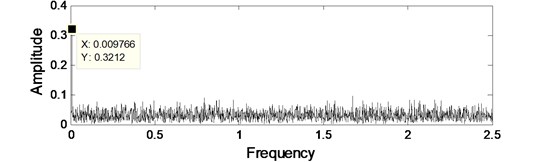
b) Spectrum of original signal
Fig. 6The decomposition results of original signal after DWT
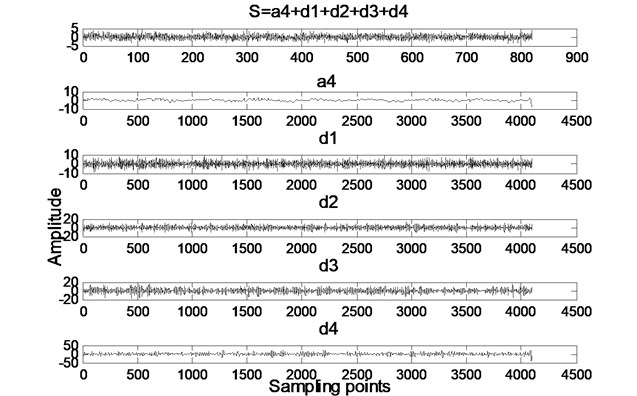
a) The time-domain components
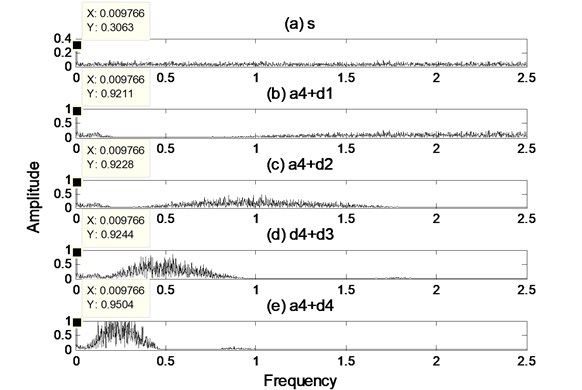
b) The spectrum components
After the input signals were processed by stochastic resonance systems in Fig. 6, we could obtain the output signal’s waveform and spectrum shown in Fig. 7. Signal detection results for a single multi-stable SR system and MCMSR system were compared in Fig. 7.
Observing the Fig. 7(a-c), we can find the original signal on the time-domain plot is difficult to identify. When it is processed by a multi-scale stochastic resonance system, we can clearly discern the periodic signal in the time-domain plot, and noise is also decreased. Observing the spectrum in Fig. 7(d-f), it is apparent that peak value at 0.01 Hz has constantly become larger. In the frequency domain of MCMSR system output, the amplitude at is equal to 2.053 which is 4 times than the original signal and 1.35 times than single stochastic resonance system output signal. This indicates that the MCMSR system has better signal enhancement and desorption capability than the multi-stable stochastic resonance system. The input SNR curves of original signal, single SR model and MCMSR model are plotted in Fig. 8 altogether. We can find that the target signal can be amplified by SR effect in the single multi-stable model and the MCMSR model. Especially, the SNR is promoted greatly in the low noise intensity region in the MCMSR model. Therefore, the MCMSR system is very effective on detection signal, and greatly improves the ability to detect weak signals.
Fig. 7Comparison of signal detection between single SR model and MCMSR model
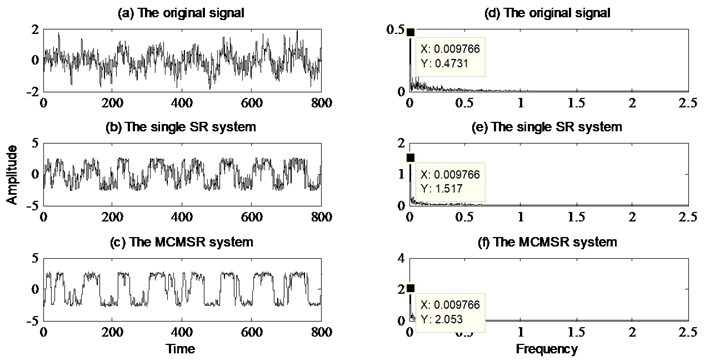
Fig. 8SNR curves of original signal, single SR model and MCMSR model
5. Application experiment
5.1. The bearing data
The experimental platform of Case Western Reserve University in US is shown in Fig. 9 [35]. The rolling bearing fault vibration signals are collected by acceleration sensors. Motor housing drive end bearing is SKF6205 in the experiment, bearing speed 1797 rpm, and the transfer frequency is 29.95 Hz. Rolling generally consists of an inner ring, an outer ring, rolling elements and cage, if the rolling bearing malfunctions, the fault frequency is predictable. We can assume that outer ring of the rolling bearing is fixed, and the inner ring is rotating with the working shaft. The pitch diameter of the bearing is , the ball diameter of the bearing is , the contact angle is , the number of rolling elements is , then the fault characteristic frequency of inner ring is as follows:
The bearing’s details geometry is provided in Table 1.
Table 1The main rolling bearing parameters
Inner diameter (mm) | Outer diameter (mm) | Pitch diameter (mm) | Ball diameter (mm) | Ball number | Contact angle / (°) |
25.001 | 51.999 | 39.040 | 7.940 | 10.000 | 0 |
Fig. 9The experimental platform

If bearing inner ring happens fault, then the characteristic frequency is equal to 162 Hz. Fig. 10 are the fault signals’ waveform and spectrum maps of bearing inner ring. Fig. 10(a) is the time domain waveform where exists a cyclical shock. Fig. 10(b) is the spectrum map where we cannot see the obvious vibration characteristics in original low frequency spectrum, and there are a lot of noise signal components, that is to say, from the original vibration signal, it is very difficult to diagnose the inner ring fault of rolling bearing.
Fig. 10The waveform and spectrum of actual signal
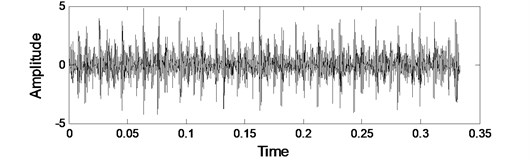
a) Waveform of actual signal
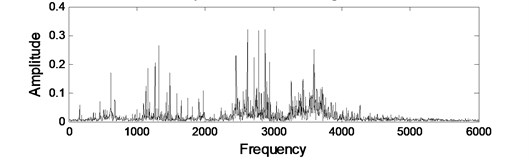
b) Spectrum of actual signal
5.2. Analysis of rolling bearing faults
In the actual signal detection and fault diagnosis, the case which meets the adiabatic approximation theory is rare. If the frequency of signal cannot occur stochastic resonance under the condition of big argument, the signal can be transformed into a frequency of small parameters; we can use the method of stochastic resonance for weak signal amplification. Based on the above ideas, scale decomposition stochastic resonance method has been studied in detail [36]. The Scale decomposition stochastic resonance is shown in Fig. 11. The specific process is as follows: First, the input signal with noise signal carry out the integration scale decomposition in order to obtain the condition of occurring stochastic resonance. Then output signal is obtained by after input signal processed by Multi-stable SR system .
Fig. 11Scale decomposition stochastic resonance

By above analysis, the method of rotating machinery fault diagnosis based on MCMSR is proposed, which is presented in Fig.12. First, we get vibration signal from the rotating machine shown in Fig. 12(a). Second, in this scenario, the spectrum of vibration signal is extracted first by FFT shown in Fig. 12(b). Third, in order to get a better effect of stochastic resonance, the second sampling signal processing through a multi-scale wavelet transform is shown in Fig.1 2(c). In this section, the high frequency energy constantly is shifted toward low-frequency part. Last, the new signal is fed back to the MCMSR model, and the system output signal is processed by Fourier transform. If the spectrum of input signal contains the fault feature frequency, the corresponding periodic component of fault will certainly be enhanced by MCMSR system, which is conducive to us to make the diagnosis of mechanical failure.
Fig. 13 shows the specific process of vibration signal by scale wavelet decomposition. Fig. 13(a) shows the decomposition result of processed signal after DWT. The scale is 4. In Fig. 13(a), is the vibration signal, is the signal’s low frequency part, to are the signal’s high frequency parts, and . Approximation signal and each scale noise signal are reconstructed respectively, and Fig. 13(b) is the spectrum of the vibration signal and the reconstructed signal. From Fig. 13 we can see that it is difficult to identify the fault characteristic frequency.
Fig. 12Principle diagram of the proposed method
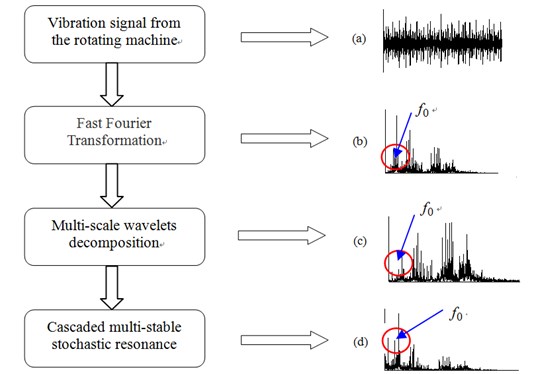
Fig. 13The decomposition results of actual signal after DWT

a) The time-domain components
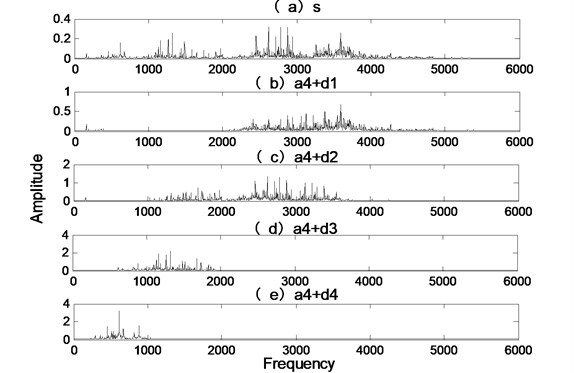
b) The spectrum components
Fig. 14The analyzed results of bearing inner race fault using signal SR model and MCMSR model
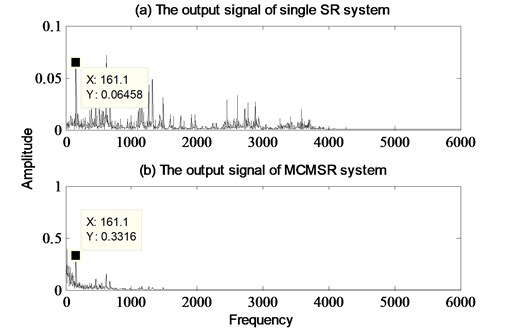
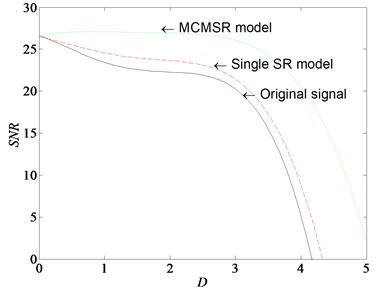
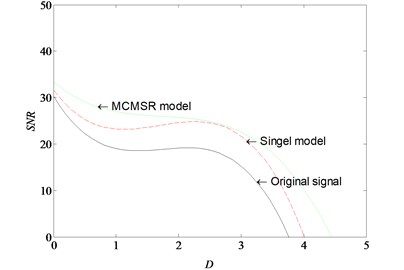
When the input signals in Fig. 13(b) are processed by stochastic resonance systems, we can obtain the results of output signal. The spectra of output signals by the single multi-stable SR method and MCMSR method are shown in Fig. 14(a) and (b), respectively. The amplitude of frequency domain output signal in Single SR system is 0.06458 shown in Fig. 14(a). In the multi-scale SR system, the amplitude of frequency domain output signal is 0.3316 which is 5.13 times than the single SR system output. The experimental results indicate that the MCMSR can effectively extract fault diagnosis characteristic from heavy background noise. The different output SNR curves of MCMSR model, single SR model and original signal are depicted in Fig. 15 together. It can be seen that the SNR of MCMSR model is higher than single SR model and original signal. At the same time, there is a wider parameter interval to keeping higher SNR for the noise intensity D. From the above analysis, multi-scale SR method has more advantages than the traditional single SR method in enhancing the fault message.
Fig. 15SNR curves of original signal, single SR model and MCMSR model
6. Conclusions
In the paper, we proposed a new weak fault diagnosis method based on multi-scale wavelet noise tuning cascaded multi-stable stochastic resonance. The method can extract useful signal from the heavy noise. In this method, the noisy signal is processed by wavelet decomposition. If the decomposed signal is a small parameter signal, it can be processed directly by stochastic resonance system. If the decomposed signal is a large parameter signal, to conform to the conditions of stochastic resonance, it must be processed by twice sampling and stochastic resonance system. Finally, the different output SNR curves of MCMSR model, single SR model and original signal are depicted altogether. It can be seen that the SNR of multi-scale SR model is higher than single SR model and original signal. Simulation and engineering experiments show that MCMSR method is very effective in solving the problem of large signal parameters. The proposed method provides an effective solution method to solve the common engineering problem of weak signal detection.
References
-
Zhang S. F., Wang Y. X., He S. L., Jiang Z. S. Bearing fault diagnosis based on variational mode decomposition and total variation denoising. Measurement Science and Technology, Vol. 27, Issue 7, 2016, p. 75101.
-
Liu J., Wang W., Golnaraghi F., Liu K. Wavelet spectrum analysis for bearing fault diagnostics. Measurement Science and Technology, Vol. 19, Issue 1, 2008, p. 105-118.
-
Osman S., Wang W. An enhanced Hilbert-Huang transform technique for bearing condition monitoring. Measurement Science and Technology, Vol. 24, Issue 24, 2013, p. 085004.
-
He Q. B., Liu Y. B., Kong F. R. Machine fault signature analysis by midpoint-based empirical mode decomposition. Measurement Science and Technology, Vol. 22, Issue 1, 2010, p. 015702.
-
Wang Z., Chen J., Dong G., Zhou Y. Constrained independent component analysis and its application to machine fault diagnosis. Mechanical Systems and Signal Processing, Vol. 25, Issue 7, 2011, p. 2501-2512.
-
Wang W., Lee H. An energy kurtosis demodulation technique for signal denoising and bearing fault detection. Measurement Science and Technology, Vol. 22, Issue 1, 2010, p. 025601.
-
Benzi R., Sutera A., Vulpiani A. The mechanism of stochastic resonance. Journal of Physics A: Mathematical and General, Vol. 14, Issue 11, 1981, p. 453-457.
-
Zhang G., Hu T., Zhang T. Q. Add to selected records characteristic analysis of power function type monostable stochastic resonance with Levy noise. Acta Physica Sinica, Vol. 64, 2015, p. 220502.
-
Lu S. L., He Q. B., Kong F. R. Stochastic resonance with Woods-Saxon potential for rolling element bearing fault diagnosis. Mechanical Systems and Signal Processing, Vol. 45, Issue 2, 2014, p. 488-503.
-
Lu S. L., He Q. B., Kong F. R. Effects of underdamped step-varying second-order stochastic resonance for weak signal detection. Digital Signal Processing, Vol. 36, 2015, p. 93-103.
-
Li G. Y., Li J. M, Wang S. B., Chen X. F. Quantitative evaluation on the performance and feature enhancement of stochastic resonance for bearing fault diagnosis. Mechanical Systems and Signal Processing, Vol. 81, 2016, p. 108-125.
-
Lai Z. H., Leng Y. G. Weak-signal detection based on the stochastic resonance of bistable Duffing oscillator and its application in incipient fault diagnosis. Mechanical Systems and Signal Processing, Vol. 81, 2016, p. 60-74.
-
He Q., Wang J., Liu Y., Dai D., Kong F. Multiscale noise tuning of stochastic resonance for enhanced fault diagnosisin rotating machines. Mechanical Systems and Signal Processing, Vol. 28, Issue 2, 2016, p. 443-457.
-
Wang J., He Q. B., Kong F. R. Adaptive multiscale noise tuning stochastic resonance for health diagnosis of rolling. IEEE Transactions on Instrumentation and Measurement, Vol. 64, Issue 2, 2014, p. 564-577.
-
Wang J., He Q. B., Kong F. R. An improved multiscale noise tuning of stochastic resonance for identifying multiple transient faults in rolling element bearings. Journal of Sound and Vibration, Vol. 333, Issue 26, 2014, p. 7401-7421.
-
Shi P. M., Ding X. J., Han D. Y. Study on multi-frequency weak signal detection method based on stochastic resonance tuning by multi-scale noise. Measurement, Vol. 47, Issue 1, 2014, p. 540-546.
-
Shi P. M., Su C. J., Han D. Y. fault diagnosis of rotating machinery based on adaptive stochastic resonance and AMD-EEMD. Shock and Vibration, 2016, p. 9278581
-
Qin Y., Tao Y, He Y., Tang B. Adaptive bistable stochastic resonance and its application in mechanical fault feature extraction. Journal of Sound and Vibration, Vol. 333, Issue 26, 2014, p. 7386-7400.
-
Chen X. H., Cheng G., Shan X. L., Hu X., Guo Q., Liu H. G. Research of weak fault feature information extraction of planetary gear based on ensemble empirical mode decomposition and adaptive stochastic resonance. Measurement, Vol. 73, 2015, p. 55-67.
-
Lei Y. G., Han D., Lin J., He Z. J. Planetary gearbox fault diagnosis using an adaptive stochastic resonance method. Mechanical Systems and Signal Processing, Vol. 38, Issue 1, 2013, p. 113-124.
-
Li J. M., Chen X. F., He Z. J. Multi-stable stochastic resonance and its application research on mechanical fault diagnosis. Journal of Sound and Vibration, Vol. 332, Issue 22, 2013, p. 5999-6015.
-
Han D. Y., Li P., An S. J., Shi P. M. Multi-frequency weak signal detection based on wavelet transform and parameter compensation band-pass multi-stable stochastic resonance. Mechanical Systems and Signal Processing, Vol. 70, Issue 71, 2016, p. 995-1010.
-
Shi P. M., Li P., An S. J., Han D. Y. Stochastic resonance in a multistable system driven by gaussian noise. Discrete Dynamics in Nature and Society, 2016, p. 1093562.
-
Shi P. M., Su X., Han D. Y. Stochastic resonance in tristable system induced by dichotomous noise. Modern Physics Letters B, Vol. 30, Issue 31, 2016, p. 1650377.
-
He H. L., Wang T. Y., Leng Y. G., Zhang Y., Li Q. Study on non-linear filter characteristic and engineering application of cascaded bisable stochastic resonance system. Mechanical Systems and Signal Processing, Vol. 21, Issue 7, 2007, p. 2740-2749.
-
Yang B. Y., Wang L. L., Ran S. H., Ye X. P., Yang J. X. Weak signal detection based on adaptive cascaded bistable stochastic resonance system. Procedia CIRP, Vol. 27, 2015, p. 292-297.
-
Zhao R., Yan R. Q., Gao R. X. Dual-scale cascaded adaptive stochastic resonance for rotary machine health monitoring. Journal of Manufacturing Systems, Vol. 32, Issue 4, 2013, p. 529-535.
-
Li B., Li J.M., Z.J. He. Fault feature enhancement of gearbox in combined machining center by using adaptive cascade stochastic resonance. Science China: Technology Science, Vol. 54, Issue 12, 2011, p. 3203-3210.
-
Shi P. M., An S. J., Li P., Han D. Y. Signal feature extraction based on cascaded multi-stable stochastic resonance denoising and EMD method. Measurement, Vol. 90, 2016, p. 318-328.
-
Raja J., Muralikrishnan B., Fu S. Recent advances in separat ion of roughness, waviness and form. Precision Engineering, Vol. 26, Issue 2, 2002, p. 222-235.
-
Zhao W. L., Liu J., Yin Y. P. Medium-low frequency signal detection based on stochastic resonance principle. Chinese Journal of Scientific Instrument, Vol. 32, Issue 4, 2011, p. 721-728.
-
He Q., Wang J. Effects of multiscale noise tuning on stochastic resonance for weak signal detection. Digital Signal Processing, Vol. 22, Issue 4, 2012, p. 614-621.
-
Zhang X. F., Hu N. Q., Hu L.,Cheng Z. Multi-scale bistable stochastic resonance array: A novel weak signal detection method and application in machine fault diagnosis. Science China: Technology Science, Vol. 56, Issue 9, 2013, p. 2115-2123.
-
Dai D., He Q. Multiscale noise tuning stochastic resonance enhances weak signal detection in a circuitry system. Measurement Science and Technology, Vol. 23, Issue 11, 2012, p. 1155001.
-
Bearing Data Center, Http://csegroups.case.edu/bearingdatacenter/pages/12k-drive-end-bearing-faut-data.
-
Ying D. X., Hu Z., Yang Y. M. The analysis of stochastic resonance of periodic signal with large parameters. Acta Physica Sinica, Vol. 61, Issue 8, 2012, p. 080501.
About this article
This work is supported by the National Natural Science Foundation of China (Grant No. 51475407), Key Project of Natural Science Research in Colleges and Universities of Hebei Province (Grant No. ZD2015050) and Hebei Provincial Natural Science Foundation of China (No. E2015203190).
