Health condition assessment of ball bearings using TOSELM

2.1. BP neural network

BP neural network was proposed by the research team headed by Rumelhart and McCelland in 1986 [21]. BP neural network is a multi-layer feedforward neural network. BP is an iterative learning algorithm, which uses generalized perceptual learning rules to update parameters in each round of the iteration. BP algorithm is based on gradient descent strategy to adjust the parameters in the negative gradient direction of the target. It is one of the most widely used neural network models.

The main characteristic of BP is that the signal is transmitted forward and the error is back propagation. In forward transfer, the input signal is processed layer by layer from the input layer through the hidden layer until the output layer. The neuron status at each level affects only the next layer of neurons. If the output layer predictive value cannot get the desired output value, then it goes to back propagation and adjusts the weights and thresholds of each layer of the network according to prediction error. After several iterations, the predicted output of BP neural network approaches the expected output. The topology structure of BP neural network is shown in Fig. 1. $X_1$, $X_2$, …, $X_n$ are the input value, $Y_1$, $Y_2$, …, $Y_m$ are the predictive value, and $W_{ij}$ and $W_{jk}$ is the network node weight in Fig. 1.

Fig. 1The topology structure of BP neural network

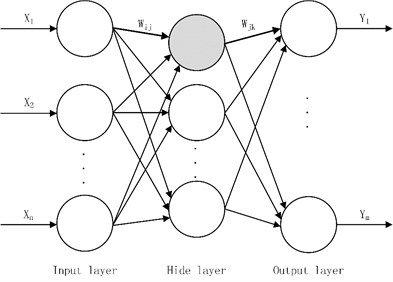
BP neural network can be regarded as a nonlinear function, and the input and predictive values of the network are independent variables and dependent variables respectively. When the input node number is $n$ and the output node number is $m$, the BP neural network expresses the function mapping relationship from $n$ independent variables to $m$ dependent variables. In the design of BP network, it is generally considered from several aspects such as the number of layers in the network, the number of neurons in each layer, the activation function, the initial value, and the learning rate.

The disadvantage of BP neural network is slow convergence, large amount of calculation, long training time, easy to fall into local minimum and not interpretable.

2.2. ELM

ELM is a new neural network algorithm proposed by Huang [23]. Compared with the traditional neural network, ELM training speed is very fast and require less manual interference. The algorithm has a strong generalization ability.

From the point of view of the neural network structure, ELM is a simple single hidden layer feedforward networks(SLFN). SLFN is shown in Fig. 2.

Fig. 2The topology structure of SLFN neural network

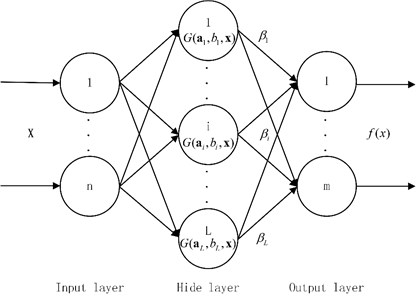
For a single hidden layer neural network, it is assumed that there are $N$ arbitrary samples (${\mathbf{X}}_i$, ${\mathbf{t}}_i$), where ${\mathbf{X}}_i=[x_{i1},x_{i2},\cdots ,x_{in}{]}^T\in {\mathbf{R}}^n$, ${\mathbf{t}}_i=[t_{i1},t_{i2},\cdots ,t_{im}{]}^T\in {\mathbf{R}}^m$. For a hidden layer network with $L$ hidden layer nodes, the neural network can be represented as follow $f\left(x\right)=\sum _{i=1}^L{\mathbf{\beta }}_{i}G\left({\mathbf{a}}_i,b_i,\mathbf{x}\right)$ where ${\mathbf{\beta }}_i$ represents the connection weight between the $i$ hidden layer neuron and the output neuron. It is a weight vector of the $m$ dimension. $G\left(\cdot \right)$ is the output of the hidden layer neuron. Parameters of the hidden layer node are ${\mathbf{a}}_i$ and $b_i$. When the hidden layer nodes are additive type, $f\left(\mathit{x}\right)=\sum _{i=1}^L{\mathbf{\beta }}_{i}g\left({\mathbf{a}}_i\cdot \mathbf{x}+b_i\right)$ where $g\left(·\right)$ is the activation function. The input weight is ${\mathbf{a}}_i$. The bias of the $i$th hidden layer node is $b_i$. The output function of the neural network can be written as follows:

where:

When $L$ is equal to $N$, Eq. (1) must have a solution. However, in practical problems, $L$ is often much smaller than $N$, that is, there is an error between the network output and the actual output, then the cost function $\mathbf{J}$ can be defined as: $\mathbf{J}=(\mathbf{H}\mathbf{\beta }-\mathbf{T}{)}^T(\mathbf{H}\mathbf{\beta }-\mathbf{T})$. How do we solve the optimal weight vector to minimize the loss function $\mathbf{J}$? ELM algorithm solves this problem in two situations:

A) If $\mathbf{H}$ is a column full rank, the best weight can be found by the least square. The solution is:

where ${\mathbf{H}}^{†}=({\mathbf{H}}^T\mathbf{H}{)}^{-1}{\mathbf{H}}^T$.

B) If $\mathbf{H}$ is not column full rank, singular value decomposition is used to solve the generalized inverse of $\mathbf{H}$ to compute the optimal weight.

BP uses gradient descent iterations to update the weights between all layers, while ELM does not adjust the weights of the input layer and the hidden layer. These weights are randomly assigned, so the training speed of ELM is very fast. Many experimental results suggest that ELM algorithm has higher learning speed and generalization performance compared with the standard BP algorithm.

2.3. OS-ELM

The on-line sequential extreme learning machine (OS-ELM) is one of the improved extreme learning machine (ELM) algorithms [20], [22-24]. It has been widely used in data fitting, classification forecasting and other fields. OS-ELM algorithm is based on single hidden layer feedforward neural networks(SLFN). So, a brief introduction of OS-ELM is given first. The output of a single hidden layer feedforward neural networks with hidden nodes can be represented by:

where the nodes number in hidden layer is $N$, the connection weight of the input layer and the hidden layer is ${\mathbf{a}}_i$ and the hidden layer threshold is $b_i$. The output weights of the $i$th hidden layer nodes to the output nodes is ${\mathbf{\beta }}_i$. The input data is ${\mathbf{x}}_j$ and the output data is ${\mathbf{t}}_j$. Assume that the input samples are $N$, and the training set of the $j$th samples is represented as:

where the input sample number is $n$ and the number of classification is $m$.

OS-ELM algorithm includes random initialization phase and online continuous learning phase. OS-ELM algorithm is described as follows.

3.1. Data description

CWRU ball bearing experiments were conducted using a 2 hp Reliance Electric motor, and acceleration data was acquired from the motor bearings. Experimental data consists of two categories: one is the normal data and the other is the fault data. The latter include inner race fault, outer race fault and ball fault. Faults ranging from 0.007 inches to 0.040 inches in diameter were introduced separately at the inner raceway, rolling element and outer raceway. Vibration fault data was recorded for motor speeds from 1797 to 1730 RPM.

The industrial ball bearing test of high speed train is carried out on NTN traction motor bearing test rig. The ball bearings used in specific type high-speed train is NTN 6311 deep groove ball bearings. In this paper, NTN 6311 ball bearing is tested on test rig. Acceleration sensor was used to collect the operation information of NTN 6311 deep groove ball bearings in order to monitor its health state. The test bearing runtime accumulates 732 hours on the test rig with a cumulative mileage of nearly 300,000 kilometers. The collected data can be divided into two types: radial vibration data of fault ball bearing and radial vibration data of normal ball bearing.

3.2. Feature extraction

The public ball bearing vibration data acquired from Case Western Reserve University Bearing Data Center. This data set has many vibration data files. This paper extracts features from the raw sensory data: B007-1.mat, B014-1.mat, Normal-1.mat, IR007-1.mat, IR014-1.mat, IR021-1.mat, 1772.mat, OR007@6-1.mat, OR014@6-1.mat, OR021@6-1.mat.

One of the challenges of assessing health condition of ball bearing lies in extracting the right correlated features. In order to obtain more comprehensive and accurate running health information and take account of the computation time, this paper selects the following features. The features include: maximum absolute value, absolute mean, peak-peak value, square mean root, kurtosis, crest factor, kurtosis factor, impulse factor, clearance factor and shape factor. The description and equations are shown in Table 1.

Absolute mean represents the vibration signal amplitude absolute mean value. It is used to describe the stability of signals. Maximum absolute value denotes the maximum amplitude value of the vibration signal waveform. Peak-peak value describes the range of signal values. Square mean root represents the vibration signal energy and its stability and repeatability are better. The larger the kurtosis indicates the more impulse component in the vibration signal. Crest factor is an important parameter to reflect the development trend of bearing faults. The kurtosis factor, impulse factor and clearance factor can effectively diagnose the incipient impulse faults. Shape factor has good stability and poor sensitivity. These features are fast and useful calculation index that can indicate the bearing health condition using vibration big data. The ten features were referred as features in this paper. Features are used to test the health state of ball bearings.

3.3. TOSELM algorithm

Many applications of OS-ELM are running in a single computer environment. When dealing with high-speed train vibration big data, it is not only time-consuming, but also not well suited to the needs of the high-speed train business. This paper develops OS-ELM algorithm through TensorFlow open source software library, in order to improve the algorithm adaptability to huge ball bearings vibration data.

TensorFlow was originally developed by the Google Brain team. It released on November 9, 2015. TensorFlow is an open source software library for machine learning. The system is flexible and can be used to develop a variety of algorithms for deep neural network models [26]. It is a complete coding framework. TensorFlow computation tasks are expressed as data flow graphs. TensorFlow has its own definitions of constants, variables, and data operations. It uses session to execute the graph.

In order to make good use of TensorFlow framework processing vibration big data, this paper proposes an improved OS-ELM algorithm named TOSELM on TensorFlow deep learning system. How does TensorFlow framework deal with ball bearing vibration big data? There are three kinds of technologies: batch generator, mutation and data flow graph can help solve this challenging problem. Tensorflow provides batch generator to process big data. First, it put the data into the queue. Second, select a TensorFlow reader, and then read the data from the queue, finally use the tf.train.batch or tf.train.shuffle_batch in order to generate custom batch size data. Meanwhile, TensorFlow introduces the concept of mutation. By mutation, it can change a variable value in the computation process, and the variable is carried into the next iteration. The concept of mutation is very consistent with the operation requirements of OSELM algorithm. The biggest characteristic of TensorFlow is the data flow graph. The data flow graph is a directed graph. The nodes in the graph represent the operations, and the edges between nodes represent the multidimensional array data involved in the computation. Tensor is the multidimensional array data. Tensor can have any dimension, and each dimension can have any length. The execution of computational graph can be regarded as the process of data flow from the input node gradually to all the intermediate nodes, and finally to the output node. TensorFlow provides great space and freedom for data calculation through data flow graph, and ensures the flexibility of algorithm implementation. Data flow graph can be used to express computation intuitively. In order to use the data flow graph, each node is symbolized, and the data flow direction indicates the order of computation process. TOSELM algorithm is shown in Table 2.