Adaptive machinery fault diagnosis based on improved shift-invariant sparse coding

1. Introduction

At present, methods of machinery fault diagnosis can be divided into three categories, they are respectively modeling based methods, signal processing based methods and intelligent diagnosis methods [1-5]. Generally speaking, there are two main steps in fault diagnosis: the first step is feature extraction of vibration signals with some signal processing tools, and the second step is the fault classification based on the extracted features in the previous step [6, 7]. How to extract features from vibration signals is one of the key problem in machine fault diagnosis. Since vibration signals usually contain non-stationary and nonlinear behaviors due to the complexity of the structure and work conditions, it is difficult to achieve an effective fault diagnosis only with the time domain or the frequency domain analysis. Hence features are extracted to indicate the characteristics of vibration signals. The conventional feature extraction methods include time-domain methods, frequency-domain methods, and time-frequency domain methods [8-10]. Features mentioned above are related to the fault, but not all of these features are useful for the classification result, so we have to select some features that are beneficial to the diagnosis result. These two works will not only waste a lot of time, while it would need several evaluation criterions to evaluate the classification result, so it is necessary to change this kind of mode for fault diagnosis.

Especially in the process of fault diagnosis, one problem that need pay attention is that for one machine, one kind of fault may correspond to several conditions, such as different loads, different speeds and so on, for example, inner race fault of a bearing can correspond to 4 different speeds, which would lead to two direct impacts, the first one is that if only one condition among all of these conditions was trained, it would get a classification result with high error while diagnosing other conditions of the same fault, it is the problem of robustness; but if we train all these data in each condition, the robustness can be improved a lot, but it sacrificed the time, because the quantity of the conditions is large.

Recently, much attention has been paid on deep learning algorithm, because of its excellent feature learning ability, especially in the field of image processing [11] and speech recognition [12]. This kind of algorithm can overcome the disadvantage of traditional feature extraction methods by extracting the sparse representation of raw signal, and this sparse representation are learned from an over-complete dictionary, so it can represent the raw signal ideally. There are also someone who have applied some methods of deep learning on fault diagnosis, Alfredo Kalaitzis etc. proposed a novel convex scheme for simultaneous online fault classification and anomaly detection in a multivariate time-series setting[13], a sparse representation based approach for recognition of power system transients was proposed by Soumi Chakraborty etc. [14], Xuefeng Chen etc. proposed a compressed sensing based on dictionary learning for extracting impulse components, which learns a sparse dictionary from a whole noisy signal itself and then employs greedy algorithms to search impulse information in the learned sparse dictionary [15], a fusion sparse coding algorithm for impulse feature extraction in machinery weak fault detection was proposed by Sen deng etc., firstly, several sparse coding algorithms are executed in parallel independently as participating algorithms, then, fusion scheme of different sparse coding algorithms are presented to improve the accuracy of sparse signal reconstruction, lastly, the proposed method is used to process aircraft engine rotor vibration signals compared with other feature extraction approaches [16], Nishchal K. Verma etc. proposed a intelligent condition based monitoring method of rotating machines using sparse auto-encoders, sparse auto encoders have the ability to learn good features from the input data in an unsupervised fashion. Sparse auto-encoders and other deep architectures are already showing very good results in text classification, speaker and speech recognition and face recognition as well [17], Jipeng Xie etc. used deep belief network for learning features from high speed train vibration signals [18], Lingli Cui etc. proposed a matching pursuit of an adaptive impulse dictionary for bearing fault diagnosis, an adaptive matching pursuit algorithm that uses an impulse dictionary is introduced in this paper for rolling bearing vibration signal processing and fault diagnosis[19], Haifeng Tang etc. proposed a latent components analysis method based on sparse representation for machinery weak fault detection [20]. Algorithms above and some other paper [21, 22] which using learned sparse dictionary for machinery fault diagnosing, can diagnose different kind of fault with lower correct rate compared to EEMD algorithms, at the same time, it would take a lot of time when data from the same kind of fault which belong to different condition.

In order to solve problems mentioned above, an improve SISC framework for machinery fault diagnosis was proposed, this method can learn useful bases from just one condition of each kind of fault, but it can be adaptive to other conditions, so it can improve the robustness of fault diagnosis, meanwhile, we improved the shift-invariant sparse coding algorithm, which make it more efficient than before.

The remaining sections of this paper are listed as follows: Section 2 described the related work used in this paper, which introduced the algorithm of SISC; the proposed framework for adaptive fault diagnosis was stated in Section 3, which included improved shift-invariant sparse coding and novel framework for adaptive fault diagnosis; experimental test was given in Section 4; at last, we concluded this paper and made some discussion.

2. Related work

3. Proposed framework for adaptive machinery fault diagnosis

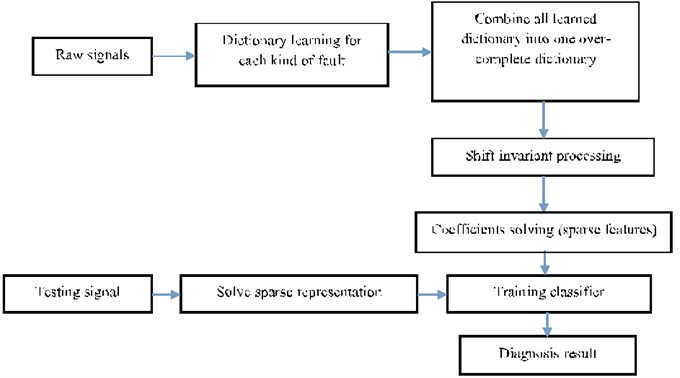
Adaptive machinery fault diagnosis algorithm is shown in Fig. 1. In order to reduce the diagnosis time and don’t reduce robustness, we first need to learn dictionary for each kind of faults, then it is essential to combine all learned dictionaries into one over-complete dictionary, after shift invariant processing, by calculating the coefficients, we obtained all new features of each fault, when we need to diagnose a data set to see which fault it belongs, we need firstly to solve sparse representation, which is the new feature representation, using the trained classifier to diagnose the new data.

Fig. 1Novel framework for machinery fault diagnosis

In order to improve the computation performance of shift-invariant sparse coding algorithm, using the idea in literature [26] to solve the problem of SISC algorithm. Firstly, which holding $d_k$ fixed, solving $s_{k,i}$ by Eq. (3). Using feature-sign search algorithm for solving:

Feature-sign search algorithm used for SISC:

(1) Initialize $s_k:=\overrightarrow{0}$, $\theta :=\overrightarrow{0}$, and “active set” $:=\left\{\right\}$, where ${\theta }_i\in \{-\mathrm{1,0},1\}$ denotes sign ($s_{k,i}$).

(2) From zero coefficients of $s_k$, select $i=\mathrm{a}\mathrm{r}\mathrm{g}ma{x}_i\left|\frac{\partial {‖X_i-d_k*s_k‖}^2}{\partial s_{k,i}}\right|$, active $s_{k,i}$ (add $i$ to “active set”) only if locally improves the objective, namely:

• If $\frac{\partial {‖X_i-d_k{s}_k‖}^2}{\partial s_{k,i}}>\beta$, then set ${\theta }_i:=-1$, “active set” $:=\left\{i\right\}\cup$ “active set”.

• If $\frac{\partial {‖X_i-d_k*s_k‖}^2}{\partial s_{k,i}}<-\beta$, then set ${\theta }_i:=1$, “active set” $:=\left\{i\right\}\cup$ “active set”.

(3) Feature-sign step: Set $A={\sum }_{k=1}^K{d}_k$, let $\widehat{A}$ be a sub-matrix of $A$ that contains only the columns corresponding to the “active set”.

Let ${\widehat{s}}_{k,i}$ and $\widehat{\theta }$ be sub-vector of $s_k$ and $\theta$ corresponding to the “active set”.

Compute the analytical solution to the resulting unconstrained QP ($\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}\mathrm{}{\widehat{s}}_k{‖X_i-d_k{s}_k‖}^2+\beta {\widehat{\theta }}^T{\widehat{s}}_k$):

${\widehat{s}}_{k,new}:=\left({\widehat{A}}^T\widehat{A}{)}^{-1}\right({\widehat{A}}^T{X}_i-\beta \widehat{\theta }/2)$,

Perform a discrete line search on the closed line segment from ${\widehat{s}}_k$ to ${\widehat{s}}_{k,new}$:

Check the objective value at ${\widehat{s}}_{k,new}$ and all points where any coefficient changes sign.

Update ${\widehat{s}}_k$(and the corresponding entries in $s_k$) to the point with the lowest objective value.

Remove zero coefficients of ${\widehat{s}}_k$ from the active set and update $\theta :=sign\left(x\right)$.

(4) Check the optimality conditions: (a) Optimality condition for nonzero coefficients: $\frac{\partial {‖X_i-d_k{s}_k‖}^2}{\partial s_{k,j}}+\beta sign\left(s_{k,j}\right)=0$, $\forall s_{k,j}\ne 0$.

If condition (a) is not satisfied, go to step (3); else check condition (b).

(b) Optimality condition for zero coefficients: $\frac{\partial {‖X_i-d_k{s}_k‖}^2}{\partial s_{k,j}}\le \beta$, $\forall s_{k,j}=0$.

If condition (b) is not satisfied, go to step (2); otherwise return $s_k$ as the solution.

Then holding $s_{k,i}$ fixed, solve $d_k$ by Eq. (4). Using the Lagrange dual for solving [23]:

4. Experimental testing

4.1. Experimental set-up

Data used in this paper for experimental testing are provided by Case Western Reserve University (CWRU), the basic layout of the test rig is shown in Fig. 2. It consists of a 2 hp reliance electric motor driving a shaft on which a torque transducer and encoder are mounted. Torque is applied to the shaft via a dynamo-meter and electronic control system. For these tests, faults ranging in diameter from 0.007 to 0.028 in. (0.18-0.71 mm) were seeded on the drive-end and fan-end bearings (SKF deep-groove ball bearings: 6205-2RSJEM and 6203-2RSJEM, respectively) of the motor using electro-discharge machining (EDM). The faults were seeded on the rolling elements and on the inner and outer races, and each faulty bearing was reinstalled (separately) on the test rig, which was then run at constant speed for motor loads of 0-3 horse power (approximate motor speeds of 1720-1797 rpm). Further details regarding the test set-up can be found at the CWRU Bearing Data Center website [27].

In order to test the improved SISC algorithm, 16 classes data were used, which include data in normal condition and in three fault condition, the used data are shown in Table 1 and Table 2.

Fig. 2CWRU bearing test rig

Table 1Training data used in this paper (–: None)

Fault diameter (in)	Load	Speed	Inner race	Ball	Outer_6	Outer_3	Outer_12
0.007	0	1797	IR007_0	B007_0	OR007_6_0	OR007_3_0	OR007_12_0
0.014	0	1797	IR014_0	B014_0	OR014_6_0	–	–
0.021	0	1797	IR021_0	B021_0	OR021_6_0	OR021_3_0	OR021_12_0
0.028	0	1797	IR028_0	B028_0	–	–	–
0 (N000, Normal)	0	1797	–	–	–	–	–

Table 2Testing data used in this paper

Fault diameter (in)	Load	Speed	Inner race	Ball	Outer_6	Outer_3	Outer_12
0.007	1	1772	IR007_1	B007_1	OR007_6_1	OR007_3_1	OR007_12_1
	2	1750	IR007_2	B007_2	OR007_6_2	OR007_3_2	OR007_12_2
	3	1730	IR007_3	B007_3	OR007_6_3	OR007_3_3	OR007_12_3
0.014	1	1772	IR014_1	B014_1	OR014_6_1	OR014_3_1	OR014_12_1
	2	1750	IR014_2	B014_2	OR014_6_2	OR014_3_2	OR014_12_2
	3	1730	IR014_3	B014_3	OR014_6_3	OR014_3_3	OR014_12_3
0.021	1	1772	IR021_1	B021_1	OR021_6_1	OR021_3_1	OR021_12_1
	2	1750	IR021_2	B021_2	OR021_6_2	OR021_3_2	OR021_12_2
	3	1730	IR021_3	B021_3	OR021_6_3	OR021_3_3	OR021_12_3
0.028	1	1772	IR028_1	B028_1	OR028_6_1	OR028_3_1	OR028_12_1
	2	1750	IR028_2	B028_2	OR028_6_2	OR028_3_2	OR028_12_2
	3	1730	IR028_3	B028_3	OR028_6_3	OR028_3_3	OR028_12_3

4.2. Test framework

4.2.1. Training results

We use half data of load 0 for calculating dictionary representation and its corresponding coefficient, and use algorithm proposed in this paper for training, and at last corresponding dictionaries of each training data were calculated, which are shown in Fig. 3.

Dictionaries calculated by improved SISC algorithm are shown in Fig. 3, sparse features of 16 kinds of bearing faults were extracted, each dictionary composed of 8 bases, this series of dictionaries indicate different vibration signal can be represented by different dictionaries. Coefficients of each base composed of the sparse features, Table 3 is the classification error rate of training features extracted by SISC algorithm using SVM algorithm.

Fig. 3Raw signal of 2 of 16 kinds of bearing faults and their corresponding dictionary with one dictionary set of 204 shift variable dictionary and W:204×8×204, (length of dictionary * number of dictionaries * shift time) x-axis of dictionary: length of the base; y-axis of dictionary: amplitude of base

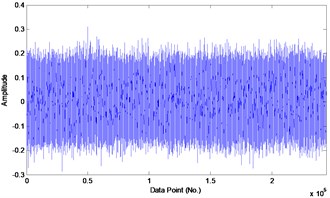
a) Data 1: (N000, Normal)

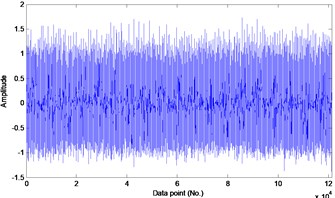
b) Data 2: (IR007_0)

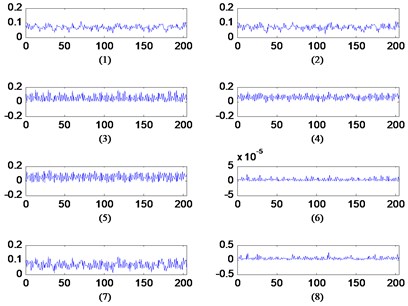
c) Data 1: Dictionary

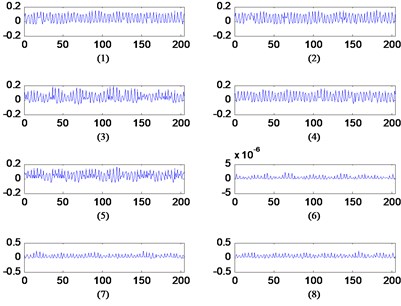
d) Data 2: Dictionary

Table 3Classification error rate of training data (–: None)

Fault diameter (in)	Classification error rates (%)
	Normal	Inner	race ball	Outer race position
				Center @6:00	Orthogonal @3:00	Opposite @12:00
0	0	–	–	–	–	–
0.007	–	0.36	0.57	0	0	0.09
0.014	–	0	1.86	1.2	–	–
0.021	–	0.96	0.89	3.75	0	0.49
0.028	–	1.24	1.76	–	–	–

4.2.2. Recognition correct rate between SISC and improved SISC algorithm

After calculating dictionary of each kind of fault, we combine all those dictionaries into one over-complete dictionary, there are a variety of method for fusing child dictionaries into one over-complete dictionary according to the needs of signal sparse representation solution, the simplest way is by connecting directly parallel combination more child dictionaries [28]:

5

$D=\left[d_1,d_2,\dots ,d_k\right],$

where $d_k$ is child dictionary, $D$ is over-complete dictionary. Connect a parallel combination more child dictionaries to one to solve the coefficient of new kind of fault, it is easy to diagnosis the fault class by training classifier with sparse represent, which can be called sparse features, using all these sparse features to train classifier, and took other half data as testing data, in this paper, SVM classifier was used [29]. In order to compare recognition correct rate between SISC and improved SISC algorithm, using features extracted by SISC and improved SISC algorithm for testing, Table 4 are classification error rate of 60 groups test data.

From Table 4 we can conclude that when using improved SISC for classing machinery fault, the classification error rate is smaller than results which using SISC algorithm, so we can gain the conclusion that algorithm proposed in this paper improved the adaptive performance of SISC algorithm for fault diagnosing.

Table 4Classification error rate of testing data between SISC and improved SISC (–: None; _1: Improved SISC, _2: SISC)

Fault diameter (in)	Load (Hp)	Classification error rates (%)
		Inner race	Ball	Outer race position
				Center @6:00	Orthogonal @3:00	Opposite @12:00
0.007	1_1	0	3.79	0.76	2.98	0
	1_2	30.00	50.22	25.78	34.87	55.13
	2_1	0	1.78	0	1.67	0
	2_2	60.54	44.76	55.34	23.20	34.76
	3_1	1.79	3.66	0	2.45	0
	3_2	30.45	24.56	44.63	43.72	50.07
	1_1	0.56	2.36	4.97	–	–
	1_2	22.78	60.79	22.54	–	–
0.014	2_1	20.65	2.98	0.65	–	–
	2_2	67.65	33.52	32.16	–	–
	3_1	40.20	1.88	2.76	–	–
	3_2	60.98	23.43	44.72	–	–
	1_1	1.34	23.26	5.47	0.78	5.63
	1_2	23.15	45.23	50.12	64.23	54.16
0.021	2_1	0.34	20.05	27.62	0	0
	2_2	33.75	55.32	67.83	53.12	12.34
	3_1	3.78	20.08	25.09	1.54	1.32
	3_2	45.20	67.39	30.65	44.91	27.63
	1_1	1.76	4.02	–	–	–
	1_2	43.78	23.89	–	–	–
0.028	2_1	4.89	4.50	–	–	–
	2_2	46.72	52.19	–	–	–
	3_1	1.87	10.34	–	–	–
	3_2	22.19	70.52	–	–	–

Table 5The running time (in seconds) for shift-invariant sparse coding algorithm and improved shift-invariant sparse coding algorithm for fault diagnosis (1: SISC, 2: improved SISC)

Fault diameter (in)	Load (Hp)	Different algorithms	Running time (s)
			Inner race	Ball	Outer race position
					Center @6:00	Orthogonal @3:00	Opposite @12:00
0.007	1	1	1.79	1.64	1.75	2.05	3.65
	1	2	0.85	0.83	0.88	1.76	3.07
	2	1	1.89	1.93	2.33	2.88	2.23
	2	2	0.87	0.72	1.90	1.34	1.02
	3	1	1.90	1.88	2.35	2.98	1.89
	3	2	0.88	0.75	1.80	1.76	0.34

4.2.3. Computation complexity

At the same time, the improved SISC algorithm has improved the efficiency of raw SISC algorithm, the running time (in seconds) for shift-invariant sparse coding algorithm and improved shift-invariant sparse coding algorithm has been listed in Table 5. In Table 5, we listed the running time of testing data 0.007 (fault diameter (in)), which include 15 group testing data.

From Table 5 we can conclude that the running time of improved shift-invariant sparse coding algorithm is less than the algorithm of shift-invariant sparse coding.

5. Conclusions

In this paper, in order to improve the adaptive performance and reduce the time used for training SISC, an improved algorithm was proposed, which using feature-sign search algorithm and Lagrange dual for solving the dictionaries and coefficients of SISC model, by experimental testing, we can obtain the result that improved SISC can meet the need of adaptive and computation complexity for fault diagnosis, which change the conventional fault diagnosis model, and obtain a better result. It improves the performance of machinery fault diagnosis in two aspect, the first one is that according to the machinery fault diagnosis in multi-condition, adaptive machinery fault diagnosis algorithm was proposed, and another one is that the computation performance SISC was improved. But there are still some problems we need to deeply consider, such as the diagnosis accuracy in this adaptive condition, although it is not a key problem at present.