Abstract
With the development of the precision guidance technology, the earth-penetrating weapon (EPW) is a huge threat to infrastructures. The objective of this research is to investigate the damage characteristics of mass concrete targets under the combined action of penetration and explosion. The validity of the penetration model is discussed by reproducing a previous experimental test reported in the literature. Meanwhile, a field test about the internal explosion in a concrete cube is conducted to verify the validity of the internal explosion model. Subsequently, damage characteristics of a mass concrete target from the upper part of a concrete gravity dam are discussed when subjected to the combined action of the penetration and explosion. In order to improve the structural performance of the mass concrete target to penetration and explosion loadings, high strength concrete material is selected as a preventive measure. Penetration processes and damage patterns of the mass target with normal and high strength concrete material are compared. Then, three internal explosion models are presented to investigate the influence of the initial penetration damage on the failure characteristics of the mass concrete target. The results show that the resistance of the mass target to the combined action of the penetration and explosion can be enhanced significantly by using the high strength concrete material. The initial penetration damage has a significant influence on the damage processes of the mass concrete target subjected to internal blast loading.
1. Introduction
With the development of the precision guided earth-penetrating weapon (EPW), hitting accuracy, drilling depth and destructive power have been improved significantly. For example, a conventional EPW named GBU-37 (contains nearly 300 kg of the high explosive), which is guided by the Global Positioning System, can penetrate 6 m of concrete or 30 m of soil before it explodes [1]. Very high accuracy increases the abilities of these weapons to destroy the shallow harden targets. The safety of important infrastructures such as the military facilities, airfield runways, underground targets, and high dams, is facing an increasingly serious threat when subjected to the attack of EPW. Therefore, it is very important to protect the structures against the combined action of the EPW penetration and explosion, which has gained great attention in recent decades [2-6].
According to different detonation mediums, there are mainly three blasting ways, i.e., air explosion [7-9], underwater explosion [9-12], and penetration explosion [13, 14]. Many researchers have conducted comprehensive experimental and numerical investigations related to air or underwater explosion effects on civil structures. However, the corresponding studies of structures subjected to the penetration explosion are limited. This is probably because of the complex processes of the penetration explosion. The penetration processes include the interaction between penetrator and solid medium, shock wave propagation, and penetration damage evolution. After the rapid penetration, the projectile will be detonated in the structure, including the initial penetration damage. It involves the explosion, shock wave and detonation products-structure (including initial penetration damage) interaction, and damage propagation. Hence a sophisticated numerical model considering the combined effects of the penetration and explosion is required to enable more realistic reproduction.
Just for the penetration processes, many researchers have carried out considerable research on the impact theory [15], experimental tests [16, 17] and numerical simulations [18]. It should be noted that the aforementioned research objectives are mainly focused on concrete slabs or blocks. Few studies have focused their attention on the damage characteristics of the mass concrete structures subjected to high-velocity impact loading.
Due to the complexity of the damage prediction of concrete structures under the attack of EPW, penetration effects are generally ignored [19-22]. There are usually two treatments: (1) the explosives are hypothetically buried in the concrete structures, as shown in Fig. 1(a). For example, Lu et al. [19] used a fully coupled numerical model to simulate the response of a buried concrete structure induced by underground blast loading. Fan et al. [20] employed both the SPH and the state-based peridynamics to simulate soil fragmentation/ejection subjected to the blast of buried explosives. (2) The charge is placed at the bottom of the prefabricated borehole in the concrete structures, and the borehole is not blocked, as shown in Fig. 1(b). For example, Lai et al. [21] conducted the explosion tests of ultra-high performance concrete columns with TNT explosives embedded at different depths. Wang et al. [22] numerically investigated the failure modes and ejection behavior of concrete materials subjected to internal blast loading based on SPH processor. However, the influence of the initial penetration damage (Fig. 1(c)) on the failure characteristics of targets to internal explosion has not been considered, which may affect the reliability of the numerical simulation results.
Fig. 1Three geometry models of internal explosion: a) Explosives are hypothetically buried in targets, b) explosives are placed at the bottom of the prefabricated borehole without blocking and c) explosives are initiated with considering the initial penetration damage
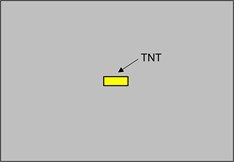
a)
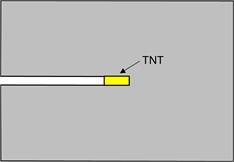
b)
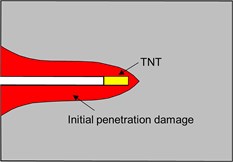
c)
In this contribution, we present a numerical approach to predict the failure characteristics of concrete structures subjected to the combined action of the penetration and explosion. The coupled SPH-Lagrange algorithm, which is used to describe the penetration processes of a high-velocity projectile, is validated by reproducing a previous experimental test reported in the literature. An internal explosion field test in a concrete cube specimen is implemented to validate the internal explosion model. Damage characteristics of the mass concrete target (from the upper part of a concrete gravity dam) under the combined action of the penetration and explosion are described. The penetration processes and damage patterns of the mass target with normal and high strength concrete materials are compared. Three internal explosion models are employed to discuss the influence of the initial penetration damage on the failure characteristics of the mass concrete target subjected to internal explosion.
2. SPH basic principles
An accurate numerical method, which is used to simulate the behavior of concrete structures under impact or blast loadings, requires three basic components: appropriate numerical techniques, a set of constitutive models, and material parameters input to the constitutive models [23]. The Lagrangian technique has the advantage of reducing the computational cost and can correctly describe the material interfaces. However, the calculation time steps will become small and the computation efficiency will decrease when the materials undergo large deformations or high velocity distorts. Compared with the traditional numerical method based on grids, the smoothed particle hydrodynamics (SPH) method can effectively simulate the large deformation for continuous materials, such as disintegration and fragmentation, and can guarantee calculation accuracy without remeshing. Hence, the SPH method is employed to analyze the damage processes and failure mechanism of the mass concrete target under the combined action of impact and blast loadings.
2.1. The formulation of SPH
SPH method uses a kernel approximation, which is based on randomly distributed interpolation points without assuming about which points are neighbors, to calculate spatial derivatives [24], as shown in Fig. 2.
Fig. 2SPH interacting with SPH
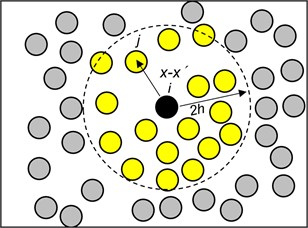
The particle will interact with other particles that are within a given distance (usually defined to be 2) from it, is the smoothing length. The interaction between particle and surrounding particles is weighted by the smoothing function . Based on the above principle, if we know the values of the surrounding particles , then, the value of a continuous function, or its derivative can be calculated at any particle , by employing the following kernel estimates:
where the angle bracket ⟨⟩ represents the kernel approximation operator. is the smoothing kernel function and should satisfy three conditions as follows:
where represents the position of the particle. is a constant defining the support domain of the smoothing function. is the Dirac delta function.
The SPH hydrodynamic formulation with material strength can be described as:
where is the mass of particle and is the density. The sum calculation involves all the SPH particles in the support domain. is the stress andmarks velocity. is the artificial viscosity, aiming to avoid unphysical oscillations. is the internal energy.
The stress tensor in Eqs. (6-7) consists of two parts: viscous shear stress and isotropic pressure :
The Jaumann rate is employed for the deviatoric stress rate to obtain the material frame in different strain rate:
where is the shear modulus, and is the Kronecker tensor. The strain rate tensor can be defined as:
The rotation rate tensor can be defined as:
The SPH particle approximation of and are as follows:
2.2. SPH-Lagrange interaction
Fig. 3 shows how the Lagrange grids interact with the SPH particles. The larger broken circle and smaller broken circle around Lagrange node represent the support region of SPH particles and background particle. When the distance between the particles and nodes is smaller than 2 (two times the smoothing length), the contact between Lagrange elements and SPH particles will happen. Lagrange grids in the support domain of SPH particle will be treated as background particles. The background particles properties are consistent with those of the corresponding Lagrange nodes, but the background particles will be treated as neighbors of SPH particle . The contact force vector between Lagrange nodes and SPH particles is estimated in the same way as the particles to particles interaction algorithm [25].
Fig. 3Lagrange elements interacting with SPH particles
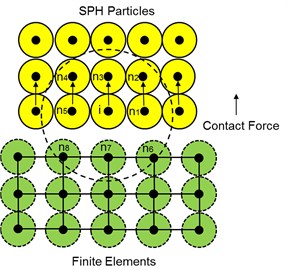
The definition of contact potential (xi):
where NCONT is defined as the neighbor particles which belong to another body to particle . is SPH kernel function. If and belong to the same body, and . marks the distance between different particles, and represents the average value of the smoothing length. In Fig. 3, for particle , NCONT = 3. The contact force will be calculated based on nodes , , . and are user-defined parameters, and marks contact stiffness penalty.
The body force is estimated as the gradient of the potential:
The contact force can be calculated as:
The SPH approximation of the gradient of the contact potential determines the direction of the contact force.
For SPH particles, the contact force is implemented in the momentum equation:
and for Lagrange nodes, the contact force is treated as the external force in the dynamic equation:
where is the acceleration of Lagrange node, and is velocity, is displacement. is the mass matrix of the system, is damping matrix and is stiffness matrix.
3. Material model and equation of state
3.1. Concrete
The dynamic properties of the concrete material are evidently different from its static properties. It has been validated that both the compressive and tensile strength of the concrete material are closely related to the strain rate. At high strain rate, the strength of concrete material improves significantly, but the effect of strain rate for tensile and compressive strength is also different [26-30]. Compressive strength can be increased by 100 %, tensile strength even increased to 600 % [26, 28].
Table 1Input data in the RHT model.
Parameter | Value | Parameter | Value |
Reference density | 2.7500e3 (kg/m3) | Brittle to ductile transition | 0.0105 |
Solid compaction pressure | 6.000e9 (Pa) | G (elastic)/(elastic–plastic) | 2.000 |
Compaction pressure | 3.000 | Elastic strength / | 0.700 |
Bulk modulus | 3.527e10 (Pa) | Elastic strength / | 0.530 |
Parameter | 3.958e10 (Pa) | Fractured strength constant | 0.700 |
Parameter | 9.040e9 (Pa) | Fractured strength exponent | 0.800 |
Parameter | 1.220 | Max. fracture strength ratio | 1.000e20 |
Parameter | 1.220 | Erosion strain | Geometric strain |
Parameter | 3.527e10 (Pa) | Erosion strain | 2.0 |
Parameter | 0 (Pa) | Type of geometric strain | Instantaneous |
Tensile strength () | 0.100 | Damage constant | 0.015 |
Shear strength () | 0.180 | Damage constant | 1.000 |
Intact failure surface constant | 1.600 | Minimum strain to failure | 0.010 |
Intact failure surface exponent | 0.610 | Residual shear modulus fraction | 0.130 |
Tens./Comp. meridian ratio () | 0.6805 | Tensile failure | Hydro |
Compressive strain-rate exponent | 0.032/0.009 a | Tensile strain-rate exponent | 0.036/0.0125 b |
aThe values of compressive strain-rate exponent are 0.032 and 0.009 for normal and high strength concrete, respectively. bThe values of tensile strain-rate exponent are 0.036 and 0.0125 for normal and high strength concrete, respectively. | |||
The dynamic behavior of the concrete material induced by blast or impact loading is a complex nonlinear and rate-dependent process. In 1993, Johnson and Holmquist [31] constructed a brittle damage model for concrete material. Based on the HJC model, Riedel et al. [32] developed RHT model. The constitutive model can describe the characteristics of the concrete material behavior at a high strain rate, and has been widely employed by researchers to simulate the dynamic response of concrete-like materials under impact or blast loading [18, 25, 33, 34]. The main parameters for the concrete RHT model are shown in Table 1.
3.2. Explosive
The explosives are typically described by using Jones-Wilkins-Lee (JWL) [35] equation of state. The JWL equation of state describes the pressure generated by chemical energy in an explosion. It can be written in the form:
where is hydrostatic pressure; is the specific volume; is specific internal energy; , , , , are material constants. is the detonation velocity. When the blasting powders are TNT, according to the explosive manual, the aforesaid parameters are respectively 6930 m/s. 6.0 GJ/m3, 1630 kg/m3, 21 GPa, 373.77 GPa, 3.747 GPa, 4.15, 0.90, 0.35.
4. Validation tests
4.1. Validation of penetration model
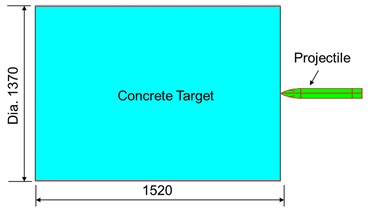
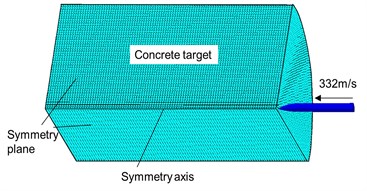
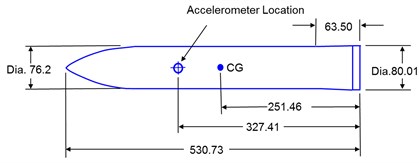
A penetration experiment tested by Forrestal et al. [36] is reproduced using the presented SPH-Lagrange coupling algorithm. In this test, a projectile with high velocity was fired into a 1.52 m long and 1.37 m wide concrete cylinder (Fig. 4). The compressive strength of the concrete target is 23 MPa, and the shear modulus is 13 GPa. Other common parameters for the RHT model are shown in Table 1. The steel projectile has an ogive nose of caliber-radius-head (CRH) 3.0 (Fig. 5). An 83-mm-diameter smooth-bore powder gun launched the projectile to strike the concrete target at a speed of 332 m/s. The mass of the projectile is 13 kg. A single-channel acceleration data recorder is structurally mounted within the projectile. Hence, the deceleration process during the penetration event can be recorded.
Fig. 4Arrangement of the projectile and the cylindrical target: a) projectile and cylindrical concrete target, dimension in mm, b) 1/4 model for numerical simulation
a)
b)
The SPH-Lagrange interaction algorithm is employed to reproduce the penetration processes of the projectile. Because both the mass loss and the deformation of the projectile are negligible [36, 37], the penetrator is treated as a rigid body. The Lagrange method is used to model the high-velocity projectile, and the SPH method is employed to simulate the damage processes of the cylindrical concrete target under impact loading. Due to the symmetry of the model, 1/4 model is adopted for this numerical model to reduce the computation cost, as shown in Fig. 4(b). The concrete target consists of 160000 particles, and the particle size is 15 mm.
Fig. 5Experimental projectile, dimension in mm: a) geometry model for the experimental projectile and b) the finite element model of projectile
a)
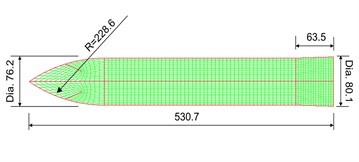
b)
Fig. 6 shows the comparisons of the projectile velocity and displacement versus time between the experimental test and numerical simulation. It can be seen that the trends of both the velocity-time curves and displacement-time curves calculated in this paper show a good agreement with the experiment test. Although the calculated penetration duration is a little longer than that from the test, the penetration depth shown in the graph represents a good approximation for this problem. The penetration depths from the experimental test and numerical simulation are 0.96 m and 1.04 m, respectively.
The final damage profiles of the cylindrical concrete target obtained from the experimental test and numerical simulation are shown in Fig. 7. It can be found that the occurring crack profile matches reasonably well with the experimental results. Many radial cracks develop from the crater to the free cylindrical surface. The average sizes of the carter diameter from the experimental test and numerical simulation are approximately 0.80 m and 0.75 m, respectively. By comparing the current results with the experiment test, it may be concluded that the SPH-Lagrange coupling model can predict effectively the penetration processes of concrete material under high-velocity impact.
Fig. 6Comparisons of the projectile velocity and displacement versus time
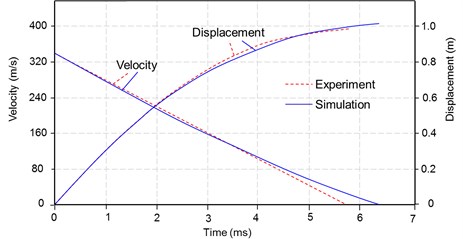
Fig. 7Final damage profiles of the cylindrical target: a) experimental test and b) numerical simulation

a)
b)
4.2. Internal blast test and numerical validation
An experimental test about the internal explosion in a concrete cube is constructed to validate the internal explosion model. For the convenience of transportation, the concrete cube is placed in a steel reinforcement cage (Fig. 8(a)). The dimensions of the concrete cube and the location of the explosives are given in Fig. 8(b). The dimensions of the concrete cube are 1.0 m×1.0 m×1.0 m. The diameter and length of the prefabricated borehole are 60 mm and 600 mm, respectively. The prefabricated borehole is filled with compact sand. Cylindrical TNT explosives are employed in the test, and the equivalent weight of the TNT charge is 0.035 kg. The distance measured from the underside of the charge to the bottom of the prefabricated borehole is 70 mm. The material properties of the concrete in the experiment test are as follows: compressive strength is 21.0 MPa, shear modulus is 13.0 GPa, density is 2450 kg/m3. Other common parameters for the RHT model are shown in Table 1.
Fig. 9 shows the numerical model of the concrete specimen subjected to an internal explosion. The internal explosion model is established based on the SPH method. RHT dynamic constitutive model is used to describe the behavior of the concrete material under blast loading. Although using smaller size particles for the concrete target will improve the accuracy of calculation, increasing the calculation cost enormously. The particle size of the concrete material is 15 mm, and the total number of the SPH particles is approximately 291000. The particle size of the charge is 5 mm, and the charge consists of 192 SPH particles.
Fig. 8Arrangement of the concrete cube: a) test setup configuration and b) the dimensions of the concrete cube, dimension in mm

a)
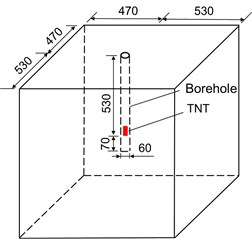
b)
Fig. 9SPH model for explosion simulation
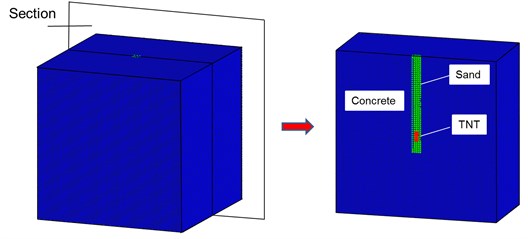
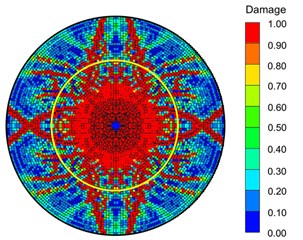
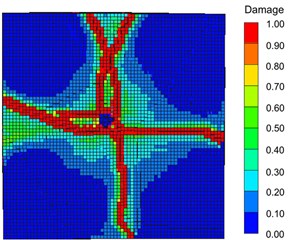
Fig. 10 shows the failure patterns of the concrete cube subjected to internal explosion. From the experimental results, it can be found that the concrete cube is broken into several pieces under blast loading. Because the explosives are not placed at the center of the specimen, the damage degree of the top side closer to the explosives is a little more serious than that far away from the charge. In the numerical simulation, the processes of damage evolution are well captured, and the results of the experimental test are also reasonably reproduced.
Fig. 10Comparisons of the experimental and numerical results: a) experimental test and b) numerical simulation

a)
b)
5. Damage characteristics of normal strength mass concrete target to penetration and explosion
5.1. Penetration processes
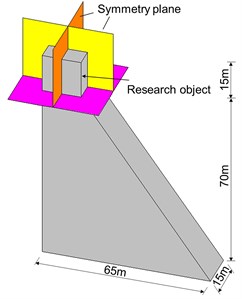
Dams are crucial lifeline engineering which contribute to the development of civilization for a long time. It is undoubted that the high dams will be the targets of the EPWs due to their significant economic and political benefits. In this paper, an upper part of concrete gravity dam, namely dam head (as shown in Fig. 11(a)), is selected as a mass concrete target. The damage characteristics of the mass concrete target with normal strength under the combined action of the penetration and explosion are investigated.
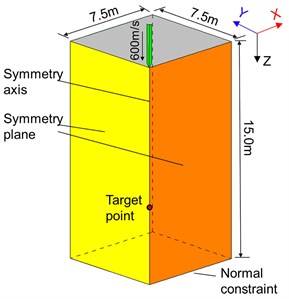
Fig. 11Penetration model of a mass concrete target: a) configuration of concrete gravity dam, b) 1/4 model of the dam head and c) numerical model for the penetration
a)
b)
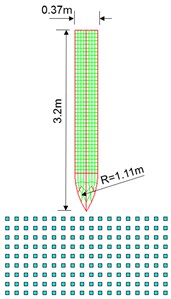
c)
Due to the complexity of the damage prediction, the upstream reservoir is not considered, and a simplified 1/4 model of the dam head is employed, as shown in Fig. 11(a-b). The dimensions of the 1/4 target are 7.5 m×7.5 m×15.0 m. Normal constraints are applied at the bottom of the target, the symmetric boundaries are applied on the symmetric planes, and other boundary surfaces are all treated as free surfaces, as shown in Fig. 11(b). The projectile has an ogive nose of caliber-radius-head (CRH) 3.0, density 7830 kg/m3, mass 2130 kg, length 3.2 m, diameter 0.37 m. The velocity of the projectile vertically striking the concrete target is 600 m/s. The concrete target is simulated by SPH particles. Fig. 11(c) shows the finite element mesh of the earth-penetrating penetrator and impact regions of the concrete target. Employing appropriate particle size is critical to obtain reliable simulation results. In this analysis, the size of SPH particles for the mass concrete target has been optimized to improve the calculation efficiency. Besides, considering the size of the mass target is 10-15 times as much as that of targets in the validation experiments. Finally, particle size of the mass target is set to 150 mm, and the total number of the SPH particles is 250000. The compressive strength and shear modulus of the concrete gravity dam (normal strength) are 35 MPa and 16.7 GPa, respectively. Other common parameters for the RHT model are shown in Table 1.
Previous studies show that when the velocity of the projectile impacting concrete target is less than 800 m/s, the projectile can be treated as a rigid body [38]. Hence, the earth-penetrating penetrator modeled by the Lagrange grids is taken as being rigid. Both the deformation and mass loss of the penetrator are ignored.
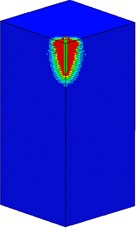
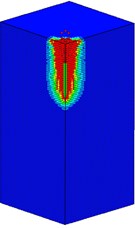
Fig. 12 shows the damage processes of the mass concrete target with normal strength subjected to the high-velocity penetrator at a speed of 600 m/s. During the high-velocity penetrating, the radial and tangential stress around the warhead are very larger than the dynamic tensile and compressive strength of concrete material. At 1 ms, the warhead and the concrete target have contacted with each other. The concrete material around the warhead is squeezed highly, thus leading to a local damage zone. With the intrusion of the projectile, the damage region of the concrete target is gradually expanding. The damage profile of the normal strength concrete target remains stable after 23 ms.
Fig. 12Damage processes of the mass concrete target (normal strength) under high-velocity penetrating

a)1 ms
b)5 ms
c)10 ms
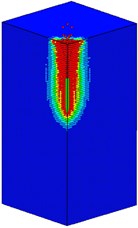
d)15 ms
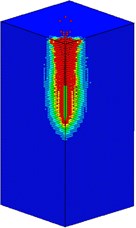
e)23 ms
Fig. 13Velocity and displacement time histories of the projectile
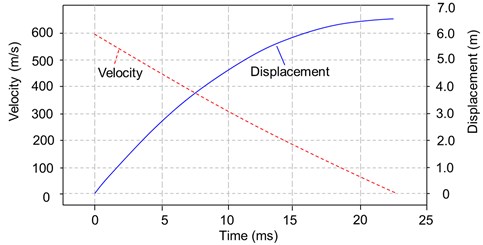
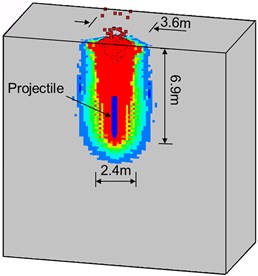
Fig. 13 shows the velocity and displacement time histories of the projectile. It can be seen that the duration of the penetration (velocity from 600 m/s to 0 m/s) is about 23 ms and the penetration depth is about 6.5 m. During the penetration processes, the projectile velocity decreases with time approximately linearly. The final damage pattern of the mass concrete target under high-velocity penetrating is shown in Fig. 14. The diameter of the crater on the top surface is about 3.6 m. The ratio of the crater diameter to the projectile diameter is about 9.7. The average diameter of the crushed zone is 2.4 m, and the ratio of the crushed diameter to the projectile diameter is about 6.5. The length of the crushed zone is about 6.9 m.
Fig. 14Final penetration damage pattern of the mass concrete target with normal strength (Through the mirror into 1/2 model)
5.2. Combined effects of penetration and explosion
When the velocity of the projectile is reduced to 0 (the penetration depth of the projectile is 6.5 m), partial projectile will be transformed into TNT charge, and the remainder projectile will be deleted. The internal explosion model with considering the initial penetration damage is shown in Fig. 15. Only 1/4 model is employed for the calculation, the same as that in chapter 5.1. The TNT equivalent of the charge is 306 kg (referred to the charge weight of GBU-37). The boundary conditions are same as that described in chapter 5.1. The TNT explosives are filled with SPH particles, and the particle size is 50 mm. The initiation point is arranged in the warhead.
Fig. 16 shows the damage processes of the concrete target (normal strength) under internal blast loading. It can be found that the mass concrete target with normal strength is destroyed severely when subjected to the combined action of the penetration and explosion. When the high-velocity earth penetrator penetrates into the mass target, the concrete material around the trajectory is damaged. After the initiation of the TNT charge, the concrete medium around the charge is in a state of intense compression, causing the damaged area expanded (Fig. 16(a)). Meanwhile, the detonation products with high-temperature and high-pressure overflow along the trajectory, resulting in the damaged area along the channel increased. At 3 ms (Fig. 16(b)), the incident shock wave interacts with the free surface, and the compression shock wave reflecting from the free surfaces results in a tensile wave. Because of the lower tensile strength of the concrete material than its compressive strength, the reflected tensile wave easily exceeds the dynamic tensile strength. Consequently, tensile damage occurs on the free surfaces. More cracks generate in the mass target, and the broken area gradually increases (Figs. 16(c-d)). The damage evolution of the normal strength concrete target remains stable after 60 ms. Many concrete particles are thrown out from the crater (Fig. 16(e)).
Fig. 15Internal explosion model with considering the initial penetration damage
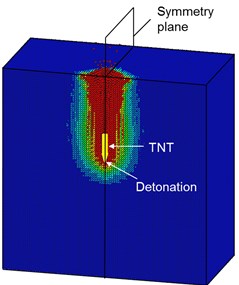
Fig. 16Damage processes of the normal strength concrete target with considering the initial penetration damage

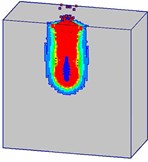
a)0.5 ms
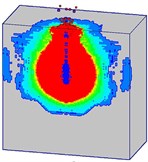
b)3 ms
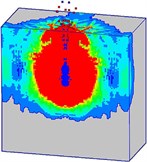
c)5 ms
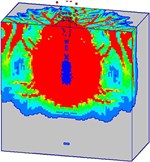
d)10 ms
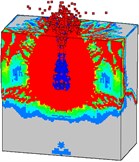
e)60 ms
6. Performance of high strength mass concrete target to penetration and explosion
In order to improve the resistance to the penetration and explosion for the mass concrete target, a high strength concrete material is employed. The compressive strength of the high performance concrete material is 140 MPa. The damage characteristics of the high strength mass concrete target under the combined effects of penetration and explosion are discussed in this section.
6.1. Penetration characteristics of high strength mass concrete target
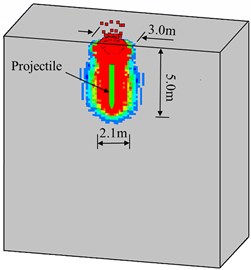
Except the strength of the concrete material, other conditions, such as the numerical model, boundary conditions, and initial penetration velocity of projectile, are the same as those in chapter 5.1. Fig. 17 shows the velocity and displacement time histories of the projectile. The final penetration damage of the high strength performance concrete target is given in Fig. 18. Numerical results show that the strength of the concrete material has important influence on the penetration depth and damage patterns of the target. The resistance of the high strength concrete target to the high-velocity projectile is much stronger than that with normal strength. The depth of penetration, crater size on the top-face, and average diameter of the crushed zone, from the simulation results are shown in Table 2. It can be observed that the penetration depth of the high-velocity projectile is significantly reduced when employing the high strength concrete material. The average diameters of the top-face crater and crushed zone all decrease approximatively by 17 % when employing the high strength concrete.
Table 2Simulation results of high-velocity penetration
Concrete strength (MPa) | Striking velocity (m/s) | Duration of penetration (ms) | Depth of penetration (m) | Diameter of the crater (m) | Average diameter of the crushed zone (m) | |
Normal strength | 35 | 600 | 23 | 6.5 | 3.6 | 2.4 |
High strength | 140 | 600 | 15 | 4.5 | 3.0 | 2.0 |
Fig. 17Velocity and displacement time histories of projectile (high strength target)
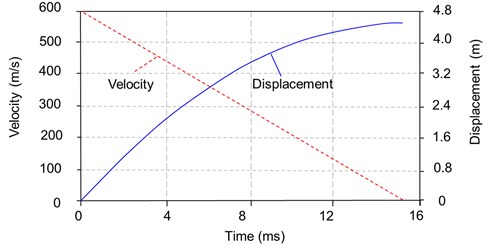
Fig. 18Final damage pattern of the high strength concrete target under high-velocity penetrating
6.2. Damage characteristics of high strength mass concrete target to internal explosion
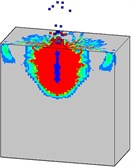
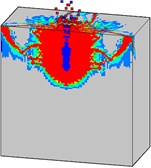
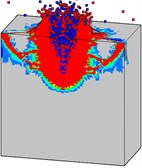
Damage progresses of the high strength mass concrete target subjected to internal explosion with considering the initial penetration damage are shown in Fig. 19. It can be found that the failure processes of the mass target with high strength concrete (Fig. 19) are evidently different from that with normal strength (Fig. 16). The penetration depth of the projectile and the strength of the concrete material are two primary factors which have significant influence on the damage characteristics of the target subjected to internal explosion loading.
Fig. 19Damage processes of the high strength concrete target to internal explosion with considering the initial penetration damage

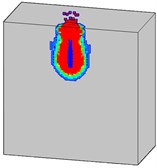
a)0.5 ms
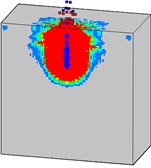
b)3 ms
c)5 ms
d)10 ms
e)60 ms
By comparing Fig. 16 (normal strength) and Fig. 19 (high strength), it can be noted that the damaged area of the target with high strength concrete is smaller in comparison to that with normal strength concrete. This is because that the penetration depth is significantly reduced when employing the high strength concrete. The blasting energy can be dissipated quickly. In addition, the resistance of the high strength target to explosion loading is stronger than that of the normal concrete target. It can be concluded that the high strength concrete material can significantly improve the resistance of the mass target to the penetration and explosion loading. The attack of the EPW will result in the complete collapse of the normal concrete target, but only cause local damage to the high strength target.
7. Influence of initial penetration damage
7.1. Internal explosion models with and without initial penetration damage
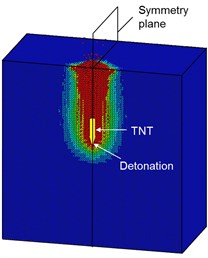
In order to investigate the effects of the initial penetration damage on the failure mechanism of the mass concrete target, three internal explosion models with and without considering the initial penetration damage are established, as shown in Fig. 20. The basic features of the three simulation cases are summarized as follows.
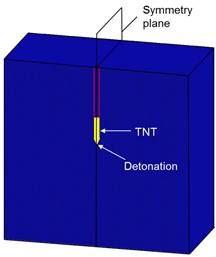
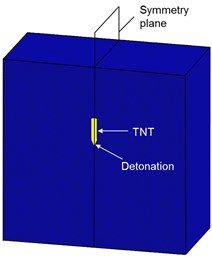
Fig. 20Three internal explosion models: a) the coupled penetration-explosion model (Case A), b) the explosives are placed at the bottom of the prefabricated borehole without blocking (Case B), c) the explosives are hypothetically buried in the concrete target (Case C)
a)
b)
c)
Case A (Fig. 20(a)): the initial penetration damage is considered by employing a fully coupled penetration-explosion model. It should be noted that the internal explosion model with considering the initial penetration damage is the same as that in Fig. 15.
Case B (Fig. 20(b)): the charge is placed at the bottom of prefabricated borehole without blocking. The diameter of the prefabricated borehole is 0.37 m, which is the diameter of the projectile. The lengths of the borehole are 6.5 m for the normal strength target, and 4.5 m for the high strength target, which are the same as the penetration depths of the projectile.
Case C (Fig. 20(c)): It is assumed that the explosives are buried in the mass concrete target.
The position and weight of the charge, initiation methods, initiation point, particle size, and boundary conditions of the above three cases are the same.
7.2. Damage characteristics of normal mass concrete target
Fig. 21 shows the damage propagation processes of the normal strength concrete target, in which the explosives are placed at the bottom of the prefabricated borehole (Case B). It can be found that damage evolution processes from Case B (Fig. 21) are similar to that from the reference Case A (Fig. 16). However, the final failure patterns from Case A and Case B are significantly different. This is because that the initial penetration damage will influence the dynamic interaction between detonation products and surrounding medium. In Case A, the concrete material around the trajectory has been damaged, and the initial trajectory further develops under the internal blast loading. More energy escapes from the trajectory in Case A than that from the prefabricated borehole (Case B). The destroyed particles are thrown out at high speed around the trajectory, which will also bring further threat to personnel and instruments. In Case B, some particles are also thrown out from the prefabricated borehole. But both the volume and velocity of the ejected particles are smaller than those in Case A.
Fig. 21Damage processes of the normal strength concrete target, when the explosives are placed at the bottom of prefabricated borehole (Case B)

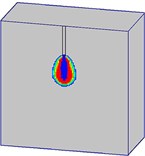
a)0.5 ms
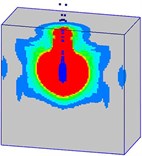
b)3 ms
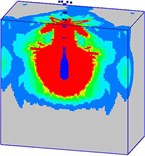
c)5 ms
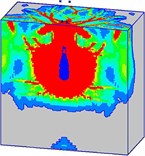
d)10 ms
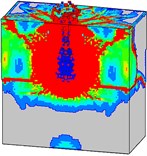
e)60 ms
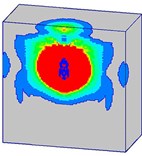
Fig. 22Damage processes of the normal strength concrete target when the explosives are buried in the target (Case C)

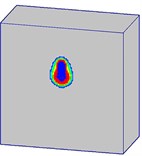
a)0.5 ms
b)3 ms
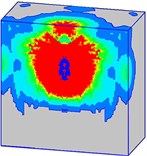
c)5 ms
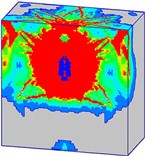
d)10 ms
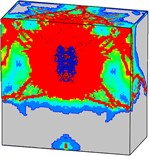
e)60 ms
Fig. 22 shows the damage propagation processes of the normal strength mass concrete target, in which the explosives are buried in the target (Case C). Unlike Case A and Case B, there is no channel for explosive products with high-temperature and high-pressure to escape in Case C. After the explosives detonation, the shock-wave and explosive products directly act on the surrounding concrete medium. Concrete material is crushed under the strong compression. More serious damage occurs on the concrete target in Case C.
Fig. 23 shows the final failure patterns of the normal concrete target subjected to different internal explosion conditions. It can be found that the initial penetration damage has significant influence on the damage characteristics of the mass concrete target subjected to internal blast loading. The damage region on the flank and bottom surfaces from Case C is the largest in the three cases. This is because that more blast energy is used to break the concrete material in Case C, and a bulge on the top surface can be obviously observed.
Fig. 23Final failure modes of the normal concrete target from different internal explosion models: a) Case A, b) Case B, and c) Case C
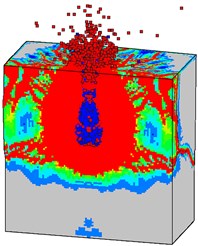
a)
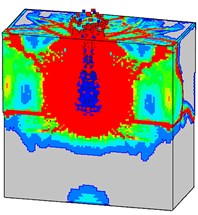
b)
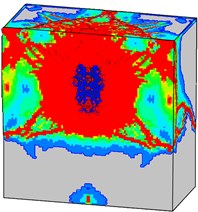
c)
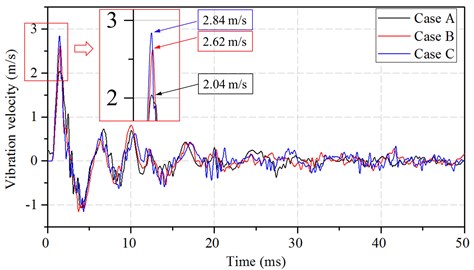
A target point is installed on the symmetry axis of the model, and the distance between the point to the bottom surface is 5.0 m, as shown in Fig. 11(b). Fig. 24 shows the Z-velocity time histories at the target point. It can be found that the velocity time histories in the above three cases are very similar. Due to the dissipation of the blast energy, the peak velocity of the target point in Case A is the minimum. The peak velocities induced by the internal blast loading in Cases A, B and C are 2.04, 2.62 and 2.84 m/s, respectively. However, because the depth of the trajectory is relatively large, the blast energy in Cases A and B cannot escape timely. Hence, the difference of the vibration velocity time histories between the above three cases is not evident.
Fig. 24Vibration velocity time histories at the target point in different internal explosion models (normal strength)
7.3. Damage characteristics of high strength concrete target
Fig. 25 shows the final damage patterns of the high strength concrete target with and without initial penetration damage under internal blast loading. In Case A, most of the blast energy escapes from the trajectory quickly, and many particles around the crater are thrown out at a high speed (Fig. 25(a)). The failure pattern of the target from Case B is similar with that from Case A. However, both the dissipation of blast energy and the volume of thrown particles from Case B are smaller than that from Case A, as shown in Fig. 25(b). Although there is no channel for the blast energy to escape at the beginning in Case C, the explosive products can also escape into the air, and concrete particles will be thrown out (Fig. 25(c)). This is because that the explosives are placed near the top surface of the target. The upper part of the target can be easily damaged and thrown out under internal blast loadings.
Fig. 25Final failure patterns of the high strength target from different internal explosion models: a) Case A, b) Case B, and c) Case C
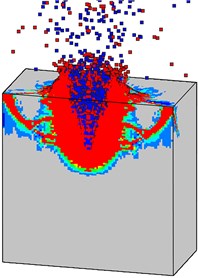
a)
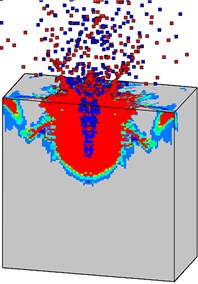
b)
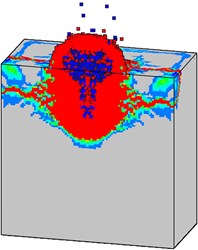
c)
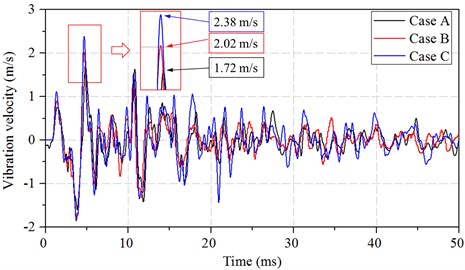
Fig. 26 shows the Z-velocity time histories at the target point in the high strength concrete structure. The influence of the initial penetration damage on the dynamic response of the target induced by the internal explosion can be observed clearly in Fig. 26. The intensity of the vibration in Case C is distinctly stronger than those in Cases A and B. The peak velocities induced by the internal blast loading in Cases A, B and C are 1.72, 2.02 and 2.38 m/s, respectively.
Fig. 26Vibration velocity time histories at the target point in different internal explosion models (high strength)
8. Conclusions
This paper is aimed to investigate the damage processes and failure modes of a mass concrete target under the combined action of the EPW penetration and explosion. The validity of the penetration and explosion models is calibrated against the experimental tests. In order to improve the penetration and explosion resistance of the mass target, high strength concrete material is selected as a preventive measure. The penetration processes and damage patterns of the mass target with normal and high strength concrete materials are compared. Besides, the influence of the initial penetration damage on the failure characteristics of the target subjected to internal explosion is investigated by establishing three internal explosion models. The following conclusions can be drawn based on the analysis results:
1) The present SPH-Lagrange coupling model can give a reliable prediction of the damage characteristics of concrete structures under high-velocity projectile, and the SPH method can simulate reasonably failure characteristics of concrete material when subjected to blast loading.
2) The penetration of the high-velocity EPW only causes local damage to the mass concrete structure. However, the subsequent internal explosion can cause serious damage to the target.
3) The resistance of the mass concrete target to the combined action of penetration and explosion can be enhanced significantly by using the high strength concrete material. The attack of the EPW will result in the complete collapse of the normal concrete target, but only cause local damage to the high strength target.
4) The initial penetration damage has a significant influence on the damage processes of the mass concrete target. The initial trajectory induced by the penetration will further develop under the blast loading, and more energy escapes from the trajectory. Hence, initial penetration damage should be taken into account to obtain more realistic results.
The combined effects of penetration and explosion on damage characteristics of structures depend on a number of different factors including the structural model, damage measure, boundary condition, projectile velocity, charge weight of EPW. Further investigations should be carried out to obtain more quantitative and qualitative conclusions.
References
-
Gronlund L. Earth-Penetrating Weapons. http://www.ucsusa.org/nuclear-weapons/us-nuclear-weapons-policy/earth-penetrating-weapons, 2005.
-
Zhao Y. T., Chu C., Yi Y. J. Study on an engineering measure to improve internal explosion resistance capacity of segmental tunnel lining structures. Journal of Vibroengineering, Vol. 18, Issue 5, 2016, p. 2997-3009.
-
Xia X., Li H. B., Li J. C., Liu B., Yu C. A case study on rock damage prediction and control method for underground tunnels subjected to adjacent excavation blasting. Tunnelling and Underground Space Technology, Vol. 35, Issue 4, 2013, p. 1-7.
-
Chen L., Jiang T. H., Gong J., Cai L. J. Study on Damage Effect of Concrete Bridge Model under Blast Loading. Applied Mechanics and Materials, Vol. 777, 2015, p. 116-120.
-
Li J., Hao H. Numerical study of structural progressive collapse using substructure technique. Engineering Structures, Vol. 52, Issue 4, 2013, p. 101-113.
-
Chen W. S., Hao H., Chen S. Y. Numerical analysis of prestressed reinforced concrete beam subjected to blast loading. Materials and Design, Vol. 65, 2015, p. 662-674.
-
Li Y., Wu W. G., Zhu H. Q. The influence of different pre-formed holes on the dynamic response of square plates under air-blast loading. Engineering Failure Analysis, Vol. 78, 2017, p. 122-133.
-
Li J., Hao H. Numerical study of concrete spall damage to blast loads. International Journal of Impact Engineering, Vol. 68, Issue 8, 2014, p. 41-55.
-
Wang G. H., Zhang S. R., Kong Y., Li H. B. Comparative study of the dynamic response of concrete gravity dams subjected to underwater and air explosions. Journal of Performance of Constructed Facilities, Vol. 29, Issue 4, 2015, https://doi.org/10.1061/(ASCE)CF.1943-5509.0000589.
-
Zhang S. R., Wang G. H., Wang C., Pang B. H., Du C. B. Numerical simulation of failure modes of concrete gravity dams subjected to underwater explosion. Engineering Failure Analysis, Vol. 36, Issue 1, 2014, p. 49-64.
-
Dodbiba G., Murata K., Okaya K., Fujitaa T. Liberation of various types of composite materials by controlled underwater explosion. Minerals Engineering, Vol. 89, 2016, p. 63-70.
-
Wang G. H., Wang Y. X., Lu W. B., et al. On the determination of the mesh size for numerical simulations of shock wave propagation in near field underwater explosion. Applied Ocean Research, Vol. 59, 2016, p. 1-9.
-
Liang L. H., Wang Z., Cao J. Z. Damaging effect of concrete by penetration and explosion of a long-rod projectile. Explosion and Shock Waves, Vol. 141, 2008, p. 138-145.
-
Li B. P. Damage effect of a concrete gravity dam under continuous attacks of guided bombs. Explosion and Shock Waves, Vol. 30, Issue 2, 2010, p. 220-224.
-
Forrestal M. J., Tzou D. Y. A spherical cavity-expansion penetration model for concrete targets. International Journal of Solids and Structures, Vol. 34, Issues 31-32, 1997, p. 4127-4146.
-
Teng T. L., Chu Y. A., Shen B. C. Penetration resistance of steel fiber reinforced concrete containment structure to high velocity projectile. Computers and Concrete, Vol. 5, Issue 6, 2008, p. 509-524.
-
Wu H., Fang Q., Chen W., Gong Z. M., Liu J. Z. Projectile penetration of ultra-high performance cement based composites at 510-1320 m/s. Construction and Building Materials, Vol. 74, 2015, p. 188-200.
-
Prakash A., Srinivasan S., Rao A. R. M. Numerical investigation on steel fibre reinforced cementitious composite panels subjected to high velocity impact loading. Materials and Design, Vol. 83, 2015, p. 164-175.
-
Lu Y., Wang Z. Q., Chong K. A comparative study of buried structure in soil subjected to blast load using 2D and 3D numerical simulations. Soil Dynamics and Earthquake Engineering, Vol. 25, Issue 4, 2005, p. 275-288.
-
Fan H. F., Bergel G. L., Li S. F. A hybrid peridynamics–SPH simulation of soil fragmentation by blast loads of buried explosive. International Journal of Impact Engineering, Vol. 87, 2016, p. 14-27.
-
Lai J. Z., Guo X. J., Zhu Y. Y. Repeated penetration and different depth explosion of ultra-high performance concrete. International Journal of Impact Engineering, Vol. 84, 2015, p. 1-12.
-
Wang H. F., Xiao J. G. J. G., Zheng Y. F. Y. F., Yu Q. B. Q. B. Failure and ejection behavior of concrete materials under internal blast. Shock and Vibration, Vol. 5, 2016, p. 1-7.
-
Clegg R. A., Hayhurst C. J., Meuric O. F. J. Combined mesh and meshfree numerical techniques to efficiently predict the response of concrete structures to impact. 6th International Conference on Structures Under Shock and Impact, Cambridge, England, 2000, p. 549-558.
-
Hayhurst C. J., Clegg R. A. Cylindrically symmetric SPH simulations of hypervelocity impacts on thin plates. International Journal of Impact Engineering, Vol. 20, Issues 1-5, 1997, p. 337-348.
-
Vignjevic R., Vuyst T. D., Campbell J. C. A frictionless contact algorithm for meshless methods. Computer Modeling in Engineering and Sciences, Vol. 13, Issue 1, 2006, p. 35-47.
-
Bischoff P. H., Perry S. H. Compressive behavior of concrete at high strain rate. Materials and Structures, Vol. 24, Issue 6, 1991, p. 425-450.
-
Fu H. C., Erki M. A., Seckin M. Review of effects on loading rate on concrete in compression. Journal of Structural Engineering, Vol. 117, Issue 12, 1991, p. 3645-3659.
-
Malvar L. J., Ross C. A. Review of strain rate effects for concrete in tension. Materials Journal, Vol. 95, Issue 6, 1998, p. 735-739.
-
Eibl J., Schmidt Hurtienne B. Strain-rate sensitive constitutive law for concrete. Journal of Engineering Mechanics, Vol. 125, Issue 12, 1999, p. 1411-1420.
-
Schuler H., Mayrhofer C., Thoma K. Spall experiments for the measurement of the tensile strength and fracture energy of concrete at high strain rates. International Journal of Impact Engineering, Vol. 32, Issue 10, 2006, p. 1625-1650.
-
Holomquist T. J., Johnson G. R., Cook W. H. A computational constitutive model for concrete subjective to large strains, high strain rates, and high pressures. Proceedings of the 14th International Symposium on Ballistics, Quecbec, Canada, 1993, p. 591-600.
-
Riedel W., Thoma K., Hiermaier S., Schmolinske E. Penetrating of reinforced concrete by BETA-B-500 numerical analysis using a new macroscopic concrete model for hydrocodes. Proceedings of 9th International Symposium on Interaction of the Effect of Munitions with Structures. Berlin-Strausberg, Germany, 1999, p. 315-22.
-
Ding Y. Q., Tang W. H., Zhang R. Q., Ran X. W. Determination and validation of parameters for Riedel-Hiermaier Thoma concrete model. Defence Science Journal, Vol. 63, Issue 5, 2013, p. 524-530.
-
Wang G. H., Zhang S. R. Damage prediction of concrete gravity dams subjected to underwater explosion shock loading. Engineering Failure Analysis, Vol. 39, Issue 4, 2014, p. 72-91.
-
LS-DYNA Keyword User’s Manual. Version 970, Livermore Software Technology Corporation, California, 2003.
-
Forrestal M. J., Frew D. J., Hanchak S. J., Brar N. S. Penetration of grout and concrete targets with ogive-nose steel projectiles. International Journal of Impact Engineering, Vol. 18, Issue 5, 1996, p. 465-476.
-
Frew D. J., Hanchak S. J., Green M. L., Forrestal M. J. Penetration of concrete targets with ogive-nose steel rods. International Journal of Impact Engineering, Vol. 21, Issue 6, 1998, p. 489-497.
-
Chen X. W., Li Q. M. Transition from non-deformable projectile penetration to semi hydrodynamic penetration. Journal of Engineering Mechanics, Vol. 130, Issue 1, 2004, p. 123-127.
Cited by
About this article
The authors gratefully appreciate the supports from the National Natural Science Foundation of China (No. 51509189), the Natural Science Foundation of Hubei Province of China (Nos. 2017ACA102 and 2017CFB666), the Open Research Fund of State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin, China Institute of Water Resources and Hydropower Research (No. IWHR-SKL-201611), and the National Key Research and Development Program of China (No. 2016YFC0402008).
Guangdong Yang designed the study, performed the research, analysed data, and wrote the initial draft of the paper. Gaohui Wang conceived of the study, designed the study and collected the data. Wenbo Lu developed the idea for the study and provided the experiment data. Peng Yan and Ming Chen contributed to the revisions and interpreted the results.
