A generalised entropy in multifractal time signals analysis of mechanical vibration

1. Introduction

The notation of complex systems, which common properties are: non-linearity, irreducibility, non-Gaussian probability distribution and statistical multiscaling of the whole system as well as of its joined elements, becomes more and more often present in various fields of science and techniques. Several definitions assuming that a complexity leads to changes and evolutions of properties as well as to adaptations of systems and processes - being effects of internal and external, slow and fast short and long-term dynamic influences - can be found in the literature. Multilevel dynamics, determinism and randomness, far from equilibrium states, accumulation of frozen accidents, are the phenomena observed at the analysis of mechanical vibrations signals, which indicate the need of simultaneous applying of mechanic and statistic rules, i.e. statistical mechanics.

The basic problems of a diagnostic task, are in this case difficulties in analytical as well experimental modelling. This fact eliminates traditional research methods using a linearization and inference on the bases of analyses of separated subsystems. Modelling of the complex systems dynamics constitutes the main challenge, which realisation becomes nearer and nearer due to advanced algorithms and calculation power of computers. The solution constitutes the application of methods based on fractal theory and entropy [1-6]. To be able to describe the multifractal dynamics, the spectrum of dimensions – called the singularity spectrum – should be determined, assuming the measure which ascribes weights to individual parts of the observed time series of data. The spectrum obtained as the segmentation result can be treated as the singularity histogram representing the local regularity degree of the investigated signal. Another way of describing local properties of time series is the multiscale analysis of probability concentration degree of the observed values and entropy of this measure constitutes the multifractal formalism base. The entropy idea, in assessing uncertainties of dynamic systems, was introduced in the information theory [7]. The information entropy of Shannon has several generalisations, such as parameterised entropy of Renyi or Tsallis [8]. A generalised correlation dimension with a parameter allows to decompose the measure due to its value. This dimension describes the way of scaling the measure in a form of the generalised Renyi entropy and is related to the multifractal spectrum by means of Legendre’s transformation [9].

Features of non-linear models – transmittance change, different frequency distribution of input and response signals, self-excited vibrations etc. – are observed during analysis of signals of mechanical vibration. This constitutes the basic information source concerning rotating machines states in the process of looking for diagnostic relations. The vibrodiagnostics of a complex systems requires observations of non-linear effects related to additional disturbance input associated with wear or damage even when a new machine can be described with sufficient accuracy by the linear model [10]. A majority of vibration real time series exhibits properties well described by means of singularity exponents representing local properties. The application of the generalised Renyi entropy for the analysis of non-linear time series of mechanical vibrations – based on the multifractal formalism - is presented in the hereby paper.

The Multifractal Detrended Fluctuations Analysis (MF-DFA) which assures stable approach to the multifractal formalism [6] and leads to determining the singularity spectra is a tool of different methods of the vibrodiagnostics. The detrended fluctuations analysis, used in investigations, constitutes an important tool in investigations of scale-variable and long-term properties as well as in the selection and classification of diagnostic features of vibration signals generated by complex rotating systems [11, 12]. Methods based on entropy idea were also used in the proposed (up to the present) solutions of the vibration signals analysis in vehicles. However, the parametrised entropy calculation, by means of MF-DFA analysis for mechanical vibration was not carried out. Another important observation is that no paper addresses the problem that in the comparative analysis of signals, assessing of entropies of higher orders is required.

The results of signals segmentations, according to multiscale energy distribution, were presented for signals recorded at various maintenance states of the vehicle drive system.

2. Renyi entropy and multifractal spectra

The signal segmentation idea, on the example of the time waveform of vibrations acceleration in the vehicle drive system, is presented in Fig. 1, according to the multiscale energy distribution.

Fig. 1Segmentation of the test signal

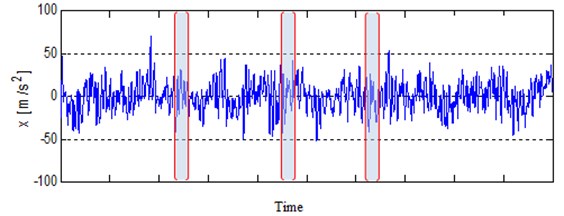
For the vibrations time series divided into segments in scale $\epsilon$ and discrete probability distribution:

where $S_i\left(\epsilon \right)$ is the sum of vibration amplitudes in the $i$th segment and $\sum S_i\left(\epsilon \right)$ is the sum of all amplitudes of the recorded signal, the Shannon entropy was determined:

The distribution of the probability density of local measures segregated into subsets acc. to $P_i\left(\epsilon \right)$ value, creates the multifractal spectrum $f\left(\alpha \right)$ of singularity exponents alpha $\alpha$, representing the local regularity degree of the tested signal.

The Shannon entropy assumes the data equivalence, regardless of their frequencies determined by the probability density distribution function – pdf. The Renyi entropy is one of the parameterised, generalised entropies [13, 14]:

The Renyi entropy exhibits very probable occurrences by means of the parameter $q\gg 0$, while when $q\ll 0$, refers to rare occurrences, forming tails of probability density distributions. The entropy defined in such way transfers more information concerning random variables and such occurrences as e.g. outliers. The scaling way of the dynamic state measure, such as the Renyi entropy, is described by the generalised correlation exponent $D\left(q\right)$, which is not increasing function of variable $q\ne \text{1}$:

It results from this dependency that the Renyi exponent can be determined from equation:

From that:

According to the multifractal formalism, the separation function (generalised sum) of the probabilistic multifractal measure, determined by Eq. (7) is scaled according to relation [15]:

where $\tau \left(q\right)$ is the generalised scaling exponent. Exponent $q$ separates various signal periods according to the probability of their occurrence. By solving double-sided logarithm of this relation the fractal measure $\tau \left(q\right)$ can be determined:

From dependencies Eqs. (6) and (8) the relation between the multifractal Renyi $D\left(q\right)$ measure and generalised multiscaled exponent $\tau \left(q\right)$ results:

In specific cases the Renyi measure reduces to other fractal dimensions. For $q=\text{0}$, it is a volumetric dimension (box type), for $q\to \text{1}$ an information dimension (in accordance with the Shannon entropy definition), while for $q=\text{2}$ – a correlation dimension expressing the probability of finding a pair of points of the phase attractor – reconstructed on the time series basis – in a distance smaller than the determined one. The mentioned connection of the multifractal spectrum with the Renyi dimension allows to assess the time series on the basis of the algorithm of Multifractal Detrended Fluctuations Analysis (MF-DFA) [16, 17], which leads to determining the generalised Hurst exponent $H\left(q\right)$ [18, 19], from the dependence describing the signal fluctuations scaling:

Generalised scaling exponent $\tau \left(q\right)$ is determined by equation:

and the multifractal spectrum $f\left(\alpha \right)$ obtained in the Legendre transformation:

when the singularity exponent $\alpha$:

Knowing the generalised scaling exponent $\tau \left(q\right)$, the Renyi entropy $q\ne \text{1}$ can be assessed from equation:

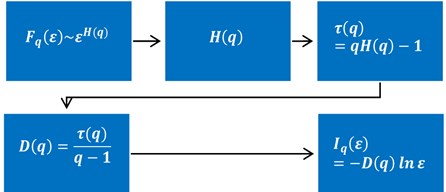
for the smallest applied observation scale of signal $\epsilon$. The algorithm idea is illustrated in Fig. 2.

Fig. 2Algorithm of determining the parameterised Renyi entropy

3. Experimental tests

Measured mechanical vibrations of the engine block constitute a combination of periodical signals related to operations of rotating elements and responses to impulse forces related to reciprocating motion and also excitations caused by gas pressures. Strong transient states in vibroacoustic signals originate from operations of inlet and exhaust valves, injectors, combustion processes, piston strokes of cylinder bushings. Some excitations occur periodically, e.g. piston strokes on cylinder bushing, opening and closing of valves (for engines with stable timing gear phases), while some are characterised by angular variabilities (injection, ignition). All these phenomena requires non-linear description even for the system in good technical condition.

The entropy is an important measure in statistical mechanics at assessing the disordered degree in non-linear dynamics of systems. It was assumed that the parameterised entropy would allow to differentiate maintenance states of vehicle drive systems on the basis of observed signals of mechanical vibrations.

Examinations were performed during road tests on the four-cylinder engine of spark ignition 1.4 dm³ with 8 valves [20-22]. Series of engine vibration measurements for various rotational speeds and loads were performed. The main measuring path included the piezoelectric vibration sensors B&K Delta Shear type 4393 of a frequency range: 0.1-16500 Hz, resonance frequency 55 kHz and work temperatures from –74 °C to +250 °C, fastened by means of a joint screwed into the engine side at cylinder 1, and the portable device for recording data B&K PULSE type 3560E. Accelerations of engine block vibrations were recorded in the vertical and horizontal directions with a frequency of 65536 Hz. Signals of vibration accelerations of the engine head were recorded from sensors mounted specially for the needs of experiments. Apart from the engine vibrations signal also the crankshaft position signal, throttle position and signals from the ignition coil at 1 and 4 cylinder were recorded. In determining the timing of interception, additional signals enabled the identification of engine working cycles, injection moments, ignition and timing of gear phases (Fig. 3).

Fig. 3The test rig

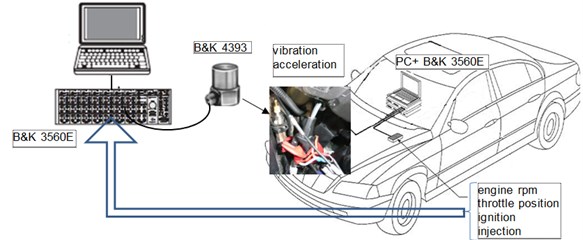
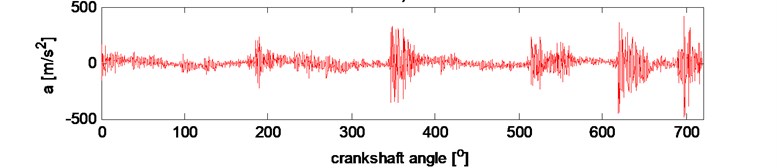
Fig. 4Resampling signal example during two revolutions of the crankshaft at 3000 rpm: a) synchronizing signal of crankshaft induction sensor, b) vibration signal in time domain (raw data), c) vibration signal in crankshaft angle domain (resampled data)

a)

b)

c)

Signals were recorded during driving with a constant speed. Small speed fluctuations were eliminated during further analysis. Maintaining the constant rotational speed of the engine is essential, since this parameter has a significant influence on the vibration amplitude. A load influence is not as important as speed. Then the signal was pre-processed with antialiasing filter to avoid amplifying the components in the natural frequency band of the vibration sensor. Using the information from the crankshaft position sensor, the vibration signal was resampled in order to equalise the number of samples analysed in each cycle of engine operations. Order tracking procedure enabled changing the domain from the time into the angle of rotation of the crankshaft, during the analysis (Fig. 4).

The resampled signal of a length of four work cycles of the SI engine (14400 samples) were divided into segments of the same length and the scale range selection within limits: $\epsilon \in$ (1/3600, 1/4).

The program of investigations contained various maintenance states, being the effect of mechanical defects, grouped into classes called symbolically: no-fault, initial wearing, and serious defect. Simulated defects constituted the different valve head cut and/or different clearance. Initial defect constituted the valve head cut 3 mm long, while serious defect had this cut increased, for example, up to 6 mm (Fig. 3). This kind of damage simulated the burning out of the valve.

Fig. 5Defective exhaust valve

Fig. 6Time waveforms of engine vibrations accelerations: a) no-fault state, b) initial defect of the exhaust valve, c) serious defect of the inlet valve

a)

b)

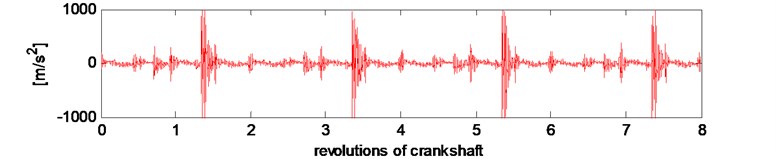
c)

States qualified for repairs or for exchanging elements are rated into the serious defect group. Instantaneous time progresses of the acceleration of vibrations during eight revolutions of crankshaft (4 working cycles of engine) for various conditions are presented in Fig. 6.

It was observed, in all mentioned types of leakage in the system: exhaust valve – cylinder, that in the time progress of vibration the signal responses for the valve opening and closing are dominating. The average results of experimental tests and multifractal analysis are shown in Figs. 7, 8.

Fig. 7Multifractal spectra of the signal of the engine vibrations acceleration

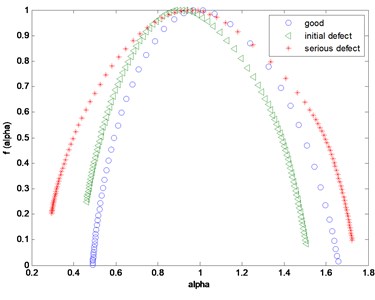
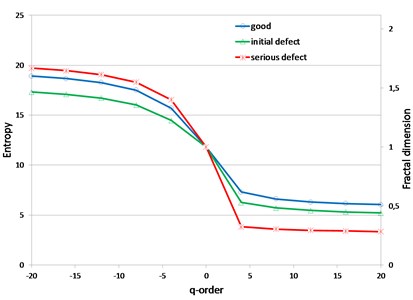
Fig. 8Parameterised entropy Iq1/3600 and the fractal dimension of the entropy of the engine vibrations acceleration signal

The performed investigations confirmed the possibility of assessing the observed states of the dynamic system, on the basis of the distribution of the parameterised Renyi entropy values. The initial wearing state causes the spectrum shifting in the direction of smaller singularities, describing segments of the series of larger amplitude fluctuations shown in Fig. 7. Thus, the fractal dimension of entropy and entropy of the most and the least energy (probable) fragments of the tested time series, related by the dependency Eq. (14), are subjected to changes. This causes small oscillations of the entropy span determined for segments of the smallest and highest fluctuations of the vibration signal, according to:

The multifractality increase and (corresponding to it) the entropy span level $\mathrm{\Delta }Iq\left(\epsilon \right)$ increase can be observed, for orders $q>$ 5 (Fig. 8), in the exhaust valve serious defect state, indicating the necessity of its repairs or exchange. This conclusion is supported by the averaged values of the parameterised Renyi entropy (of selected orders) for time series of vibrations accelerations in the tested states of the engine valve system, shown in Table 1.

4. Conclusions

The experiment performed with implemented defect as well as in good technical condition of the drive system confirmed the multifractal character of the mechanical vibrations signals of the block of the spark ignition engine. The investigated systems dynamics can be described by means of the set of fractal dimensions forming the singularity spectrum. The spectrum width indicates the multifractality level. The parameterised Renyi entropy is (in a simple way) related to multifractal generalised fractal dimensions. It was shown that the study of the higher order parametrized entropies, obtained with the proposed method, gives useful information hidden in the vibration signals and can be used as the diversification measure for the identification of the states qualified for repairs or for exchanging elements.