Measurement method of torsional vibration signal to extract gear meshing characteristics

2.1. Signal acquisition

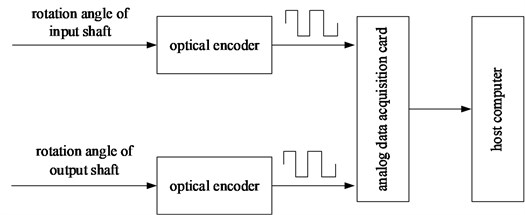
The signal acquisition system is composed of two optical encoders, an analog data acquisition card and a host computer, as shown in Fig. 1. One of the two optical encoders is installed on the input shaft of the gear pair, whereas the other is installed on the output shaft, both of which rotate with the shafts and output $N$ pulses every revolution, where $N$ represents the number of optical encoder segments. The pulse signals generated by the two optical encoders are collected using the analog data acquisition card and preserved to the host computer; the signals are then processed in MATLAB to obtain the torsional vibration signal of the gear (the signal processing will be described in detail later).

The measurement accuracy of the signal acquisition system depends on the number of optical encoder segments and sampling precision of the analog data acquisition card. The rotation angles of the shafts are essentially sampled on a uniform angular interval basis, and each output of a pulse indicates that the shaft has rotated 360°/$N$. Thus, the larger the $N$, the higher the angular resolution of the optical encoder is. The sampling precision of the analog data acquisition card depends on its clock frequency; the higher the clock frequency, the more sampled points of the pulse signal are collected in the same time so that a higher time resolution is obtained.

To accurately measure the rotation angles of the input and output shafts of the gear pair at a high frequency, an incremental optical encoder with 2500 segments is selected, with a maximum speed of 3000 rpm. The angular resolution of the optical encoder can reach 0.144°. Given a shaft rotation speed of 3000 rpm, the sampling frequency of the analog data acquisition card $f_s$ should satisfy the condition Eq. (2), in accordance with the Nyquist-Shannon sampling theorem:

For the time-domain waveforms of the torsional vibration signal to accurately reflect the meshing characteristics of the teeth, a high-precision analog data acquisition card NI PXI-5152 with two analog input channels has been selected; the sampling rate of each channel can reach 1 Gs/s. The PXI-5152 is embedded into the NI PXI-1031 chassis, equipped with NI PXI-8106 real-time controller.

Fig. 1Block diagram of a signal acquisition system

2.2. Signal processing

In the measurement method, the pulse signals of the input and output shafts are firstly counted and interpolated to obtain the initial torsional vibration signal in MATLAB. Subsequently, on the basis of the MATLAB wavelet toolbox, the initial torsional vibration signal is subjected to a discrete wavelet transform to obtain the torsional vibration signal of the gear. This method avoids using the complex hardware counting circuit and the demodulation circuit, which is in accord with the development trend of the measurement technique to virtual instrumentation.

2.2.2. Discrete wavelet transform

The study by [18] assumed that the Fourier transform of the function $\psi \left(t\right)$ satisfies $\widehat{\psi }\left(0\right)=0$, and the function cluster ${\psi }_{a,b}\left(t\right)$, which represents the translation and dilation of the function $\psi \left(t\right)$, is called the wavelet function:

3

${\psi }_{a,b}\left(t\right)={\left|a\right|}^{-\frac{1}{2}}\psi \left(\frac{t-a}{b}\right),\mathrm{}\mathrm{}\mathrm{}\mathrm{}\left(a,b\in R,\mathrm{}\mathrm{}\mathrm{}\mathrm{}a\ne 0\right),$

where $\psi \left(t\right)$ is called the mother wavelet, $a$ represents the scale parameter, and $b$ is the translation parameter.

The continuous wavelet transform of the signal $f\left(t\right)$ can then be defined as:

4

$CW{T}_{a,b}={\left|a\right|}^{-1/2}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{\psi }_{a,b}^{\mathrm{*}}\left(\frac{t-b}{a}\right)f\left(t\right)dt,$

where ${\psi }_{a,b}^{\mathrm{*}}\left(t\right)$ is the conjugate function of ${\psi }_{a,b}\left(t\right)$.

To fit with the requirements of numerical computation by computer, the scale parameter $a$ and the translation parameter $b$ are generally discretized. Given $a=2^j$ and $b=k{2}^j$, the discrete wavelet transform of the signal $f\left(t\right)$ can be expressed as:

5

$DWT=2^{-j/2}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\psi (2^{-j}t-k)f\left(t\right)dt.$

In practical engineering, signals are often discrete, which can be represented by $f\left(n\right)$, $(n\in N_{+})$. The discrete wavelet transform of the signal $f\left(n\right)$ is:

6

$DWT\left(j,k\right)=2^{-\frac{j}{2}}\sum _{n=-\mathrm{\infty }}^{+\mathrm{\infty }}f\left(k\right)\psi \left(2^{-j}n-k\right),\mathrm{}\mathrm{}\mathrm{}\mathrm{}\left(j,k,n\in Z\right).$

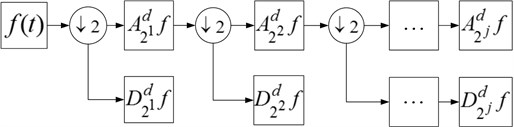
For any signal, the discrete wavelet transform first decomposes the signal into the approximate part and the minutiae part. The approximate part is further decomposed into the new approximate part and the new minutiae part, iteratively decomposed up to scale $j$. The decomposition process is shown in Fig. 2. The discrete wavelet transform decomposes a signal into a series of independent frequency bands, whereas the torsional vibration signal of a gear behaves as the meshing frequency and the frequency multiplication in the frequency domain. Therefore, as long as the appropriate decomposition layer is selected, the torsional vibration signal of the gear can be extracted from the initial signal. Notably, the “db44” wavelet is selected as the mother wavelet to extract the meshing characteristic of the gear in this study because it is similar to the torsional vibration signal of the gear.

Fig. 2Discrete wavelet transform

3.1. Modeling

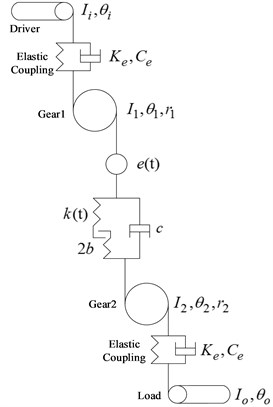
In accordance with the reference [19, 20], the dynamic model of the gear system is established, as shown in Fig. 3. The system includes a drive motor, a load motor, a spur gear pair, and two elastic couplings. The gears are perfect involute spur gears with no modifications. The nonlinear characteristic of the gear meshing process is represented by the elastic element with backlash and the damping element, whereas the elastic coupling is represented by the elastic element and the damping element. Both the mass moments of inertia of the elastic couplings and friction on the gear meshing surface are neglected.

In Fig. 3, $I_i$, $I_o$, $I_1$ and $I_2$ represent the mass moments of inertia of the diver, load, gear 1 and gear 2, respectively; ${\theta }_i$, ${\theta }_o$, ${\theta }_1$, and ${\theta }_2$ represent the rotation angles of the diver, load, gear 1 and gear 2, respectively. The base radii of gear 1 and gear 2 are $r_1$ and $r_2$, respectively. $k\left(t\right)$ and $c$ are the mesh stiffness and the damping coefficient of the gear pair. Meanwhile, $K_e$ and $C_e$ denote the mesh stiffness and the damping coefficient of the elastic couplings. $e\left(t\right)$ represents the manufacturing and assembly errors of the gear system, and the backlash of the gear pair is denoted by 2$b$.

When the drive motor and the load motor apply torques $T_i$ and $T_o$, respectively, the dynamic equation of the gear system is:

where $T_1$ and $T_2$ are the torques transferred by elastic coupling 1 to gear 1 and by elastic coupling 2 to the load, which can be expressed as:

Fig. 3Dynamic model of the gear system

Gear backlash nonlinearity is modeled as a piecewise linear function:

As gears rotate, the fluctuation of the number of tooth pairs in contact leads to the variation in mesh stiffness. The time-varying mesh stiffness $k\left(t\right)$ can be represented with the multi-order fitting stiffness model proposed in [19], which is defined as:

where $k_0$ is the average mesh stiffness; $f_m$ is the mesh frequency; ICR is the involute contact ratio; $k_r$ and ${\varphi }_r$ are the $r$th Fourier coefficient and the phase angle of $k\left(t\right)$, respectively $R=\text{5}$.

The damping coefficient c of the tooth mesh is determined using Eq. (10):

where $\zeta$ is the damping ratio.

In accordance with [21], the harmonic function can be used to represent the manufacturing and assembly errors $e\left(t\right)$:

where $e_0$ and $e_r$ represent the constant value and the amplitude of error, with $e_0=\text{0}$ and $e_r=\mathrm{}$2×10^-4 m, and $n$ is the rotation speed of shafts.

The simulation parameters of the gear system are shown in Table 1, where gear1 has the same parameters as gear 2.

3.2. Simulation results analysis

Fig. 4 presents the simulation curve of the initial torsional vibration signal obtained by simulating the dynamic model of the gear system on the basis of the Simulink platform and by using the aforementioned measurement method under the rotation speed of 2040 rpm and torque of 60 N·m. As shown in the Fig. 4, the initial torsional vibration signal has a low-frequency signal with large amplitude induced by manufacturing and assembly errors, making it difficult to directly observe the waveforms of torsional vibration (high-frequency signal).

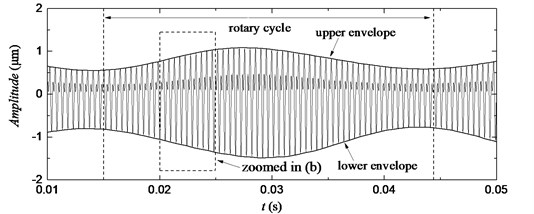
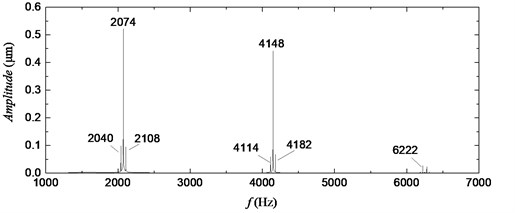
To extract the torsional vibration signal of the gear, the discrete wavelet transform is used to decompose the initial torsional signal at the scale of five in the MATLAB wavelet toolbox. After filtering the approximate part of the signal and the first three layers of detail signals, the time-domain waveforms of the remaining detail signal is shown in Fig. 5(a). At the rotation speed of 2040 rpm, the theoretical value of the first-order mesh frequency of the gear is 2074 Hz, whereas the theoretical value of the second-order mesh frequency of the gear is 4148 Hz. Fig. 5(c) shows that the FFT spectrum of the remaining detail signal contains the first-order and the second-order mesh frequency of the gear. Therefore, the remaining detail signal can be regarded as the torsional vibration signal of the gear, verifying the feasibility of the proposed measurement method.

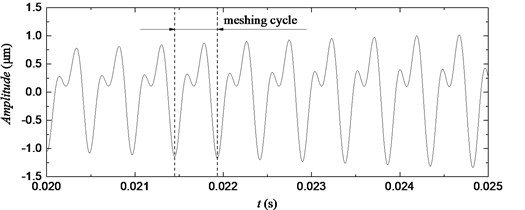
The time-domain waveforms of gear rotary cycle have been shown in Fig. 5(a), while Fig. 5(b) presents the zoomed area of the time-domain waveforms with each meshing cycle shown clearly. The meshing waveforms of the gear pair should theoretically be equal in amplitude and consistent in shape. However, the amplitudes of the meshing waveforms of the gear pair in Fig. 5(a) and Fig. 5(b) change periodically, and the shape is not uniform. In addition, on both sides of the mesh frequency is a side-band modulation; the modulation frequency is the rotation frequency of shafts, as shown in Fig. 5(c). The fault information on the gear (manufacturing and assembling errors) is included in its torsional vibration signal. Therefore, the meshing waveforms of the gear can be used to evaluate the meshing state of the gear and provide a basis for the fault diagnosis of the gear or the quality assessment of gear machining.

Fig. 4Simulation curve of initial torsional vibration signal

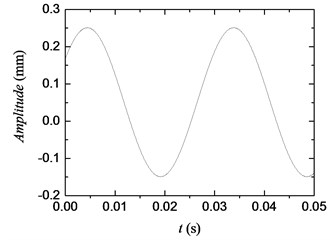
Fig. 5Simulation results after filtering with the use of discrete wavelet transform

a) Waveforms of the remaining detail signal

b) Zoomed area of a)

c) FFT spectrum of the remaining detail signal

4.1. Experimental bench

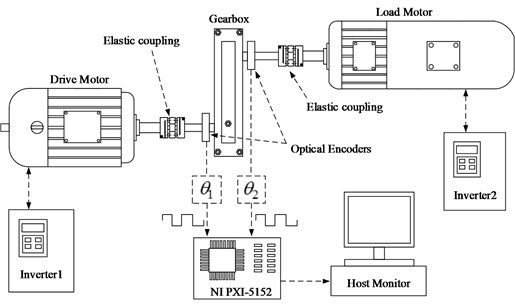
To verify the feasibility of the proposed measurement method, an experimental bench was set up, as shown in Fig. 6. The experimental bench mainly consists of a drive motor, a load motor, a gearbox with a spur gear pair, two elastic couplings, two optical encoders and two inverters. The experimental bench can be used under different working conditions by controlling the output speed of the drive motor and the output torque of the load motor with the use of inverters (not shown in Fig. 6). The two gears are involute spur gears with no modifications, and both have 61 teeth. The measuring principle of the experimental bench is shown in Fig. 7. The software aspect of the measurement system is based on the graphical programming software LabVIEW.

Fig. 6Experimental bench of the gear system

Fig. 7Measuring principle of the experimental bench

4.2. Experimental results analysis

The curve of the initial torsional vibration of the experimental bench at the rotation speed of 2040 rpm and torque of 60 N·m was obtained using the aforementioned measurement method, as shown in Fig. 8. The signal also contains a low-frequency signal with large amplitude owing to manufacturing and assembly errors, impeding direct observation of the meshing characteristics of the gear.

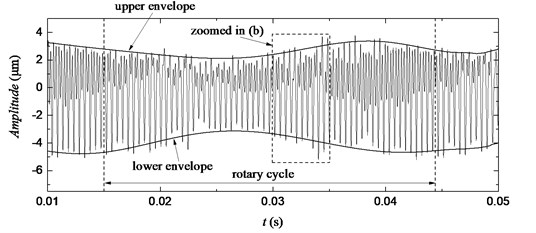
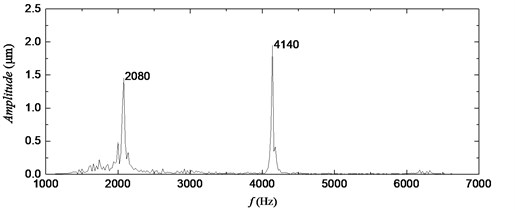
As shown in Fig. 9(c), the first-order mesh frequency and the second-order mesh frequency of the remaining detail signal are very close to the theoretical value. The small difference in frequency indicates that the remaining detail signal is the torsional vibration signal of the gear, thus verifying the feasibility of the proposed method for extracting the torsional vibration signal of gears at a high frequency. Notably, to ensure the accuracy of the final meshing waveforms, the selected sampling frequency of each channel of NI PXI-5152 is 500 MHz, and the number of sampled points reaches the maximum of 25 M. In this case, the frequency resolution of the FFT spectrum of the signal is only 20 Hz. Therefore, the difference between the mesh frequency of the measured signal and the theoretical value is within the acceptable range.

Fig. 8Measured curve of initial torsional vibration signal

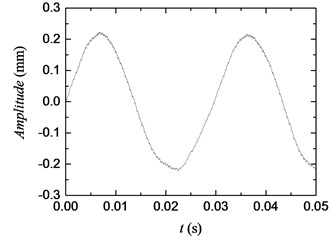
Fig. 9Experimental results after filtering with the use of discrete wavelet transform

a) Waveforms of the remaining detail signal

b) Zoomed area of a)

c) FFT spectrum of the remaining detail signal

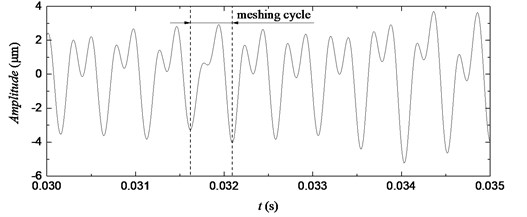
The experimental time-domain waveforms of gear rotary cycle have been shown in Fig. 9(a), while Fig. 9(b) presents the zoomed area of the time-domain waveforms with each meshing cycle shown clearly. The meshing waveforms of the gear pair in Fig. 9(a) and Fig. 9(b) show periodical amplitudes, indicating the eccentricity (uneven machining quality) of the test gears. The gear meshing waveforms obtained by the proposed method correspond to the teeth, which could reflect the meshing state of each tooth.

The upper/lower envelopes of the simulated signal and the experimental signal have been respectively shown in Fig. 5(a) and Fig. 9(a). The envelopes in the two figures have the similar trends and their fluctuation periods are similar with the corresponding rotary cycle respectively, verifying the feasibility of the proposed method further. The more specific fault signal of gears can be further obtained by the Hilbert transform, wavelet packet analysis, or other processing on the torsional vibration signal, but this subject will not be discussed in this study, which focuses on the convenient and effective measurement of the torsional vibration signal of gears.