Abstract
The blasting for bedrock excavation on land for open channel project has a great influence on lock gate in Taishan Nuclear Power Station, therefore, based on blasting vibration monitoring data, the attenuation law of blasting vibration signal has been studied through regression analysis of practical test data by Sadaovsk empirical formula and corresponding time-frequency characteristics was analyzed by Empirical Mode Decomposition based on Hilbert-Huang transform. As for those monitoring data, the results of blast vibration velocity for vertical direction are generally larger than horizontal radial and horizontal tangential direction in the near field of blasting source and the peak particle velocity of vertical direction is usually lower than horizontal radial and horizontal tangential direction in the far field of blasting source; at the same time, their main vibration frequency mostly vary from 10 Hz to 80 Hz which is much higher than natural frequency of lock gate and is beneficial to structural safety and stability of surrounding rock mass for reducing the probability of resonance. To ensure the safety of lock gate, it is of great significance to control maximum explosive weight per delay in advance for different distance from monitoring point to the explosion source according to Safety Regulations for Blasting (GB6722-2014), which shows the excellent effect on blasting damage control of the lock gate and surrounding rock mass. The results from the analysis can be for reference to similar blasting design and blasting construction.
1. Introduction
With the rapid development of national economy and the sustainable progress of science technology, the blasting technology is increasingly applied to engineering field such as highway excavation, channel blasting compaction, mining, building demolition, seismic exploration and explosive fabrication [1, 2]. Blasting stress wave is unavoidable in engineering blasting, which brought a series of serious problems such as ground vibration, blasting slungshot, building crack, landslide, tunnel collapse and many other hazards; therefore, the research on safety control on blasting vibration effect has the vital significance [3, 4].
At present, the research on effect of blasting vibration mainly concentrate on architectural structure, highway on ground, coal mining and shallow tunnel, Wei [5] theoretically analyzed the time-distance effect of blasting seismic waves from a point explosion source based on several examples of blasting near to buildings in Guangzhou and the vibration responses of structure and non-structure of buildings were calculated by the time-distance effect analysis method. Wang [6] monitored the surface building vibration to control and evaluate the impact of the underground blasting vibration on the surface building during the excavation of a big span tunnel in underground of the downtown areas with intensive buildings at Huangnipang shallow light rail station in Chongqing city. Jiang [7] analysed vibration data and adopted several vibration damping technologies to actualize large blasting excavation in a city with background of a garden building foundation and an underground garage excavation blasting. Lin [8] studied the stability control technology of tunnel and the field monitoring technique which is used to obtain the blasting vibration velocity and regression analysis result according to the modern information construction theory in the Damaoshan tunnel when blasting construction on new-built tunnel. Zeng [9] studied effect of blasting vibration on stability of surface buildings in order to mine the shallow remnant antimony ore in Wulongdao mining area and to ensure the security of the surface architecture during underground mining blasting. Wang [10] researched blasting vibration effect of coalmine soft rock roadway excavation and its impact on roadway loose circle radius based on testing and analysis of blasting vibration and excavation damage zone. Zong [11] studied the frequency spectrum characteristics and energy distribution of blasting seismic wave signal in coalmine roadway excavation by using the HHT method and EMD decomposition. Huo [12] studied failure mechanism of the dams and tunnel structures in different blasting method and put forward a blasting safety rule for the hydraulic structures. Xu [13] and Jiang et al. [14] discusses blasting vibration monitoring and blasting control technologies in construction of cross tunnels with super small interval in the space and parallel tunnels with small interval on the plane based upon field monitoring data.
However, it has seldom referred to vibration effect of the blasting for rock excavation in nuclear power station. Along with the fast social and economic development, energy problem is becoming much more urgent. Nuclear power has a giant using value as a clean and economic energy. In the process of nuclear power station construction, blasting method still has an important role as an available and relatively economic method, it inevitably involve blasting vibration monitoring and initiative control of blasting damage [15, 16]. The study on how to determine vibration characteristics of blasting vibration signal has importantly and imminently practical significance. The blasting for bedrock excavation on land for open channel project is conducted in Taishan Nuclear Power Station, which has a great influence on lock gate and surrounding rock mass, therefore, based on blasting vibration monitoring data, the attenuation law of blasting vibration signal has been studied through regression analysis of practical test data by Sadaovsk empirical formula and corresponding time-frequency characteristics was analyzed by Empirical Mode Decomposition based on Hilbert-Huang transform. At the same time, according to Safety Regulations for Blasting (GB6722-2014), the technical measures such as controlling the maximum explosive weight per delay and millisecond delay blasting is put forward for reducing the blasting effect, which shows the excellent effect on blasting damage control of the lock gate and surrounding rock mass.
2. Theory
2.1. Characteristics of wave propagation
Assuming structural body vibrate for the effect of disturbance, according to elasticity theory and wave theory, we can find that:
where is the stress of structure body for blasting, is elastic modulus, is strain and , is particle vibration velocity, propagation speed of vibration wave, respectively.
Substitution of Eq. (2) into Eq. (1) gives:
It can be seen from Eq. (3) that the stress of the structure for blasting is proportional to vibration velocity of the particle and that the particle vibration velocity is an important physical quantity of structural damage where the speed of vibration can reflect the blast-induced damage and the test is convenient and reliable.
In general, ground vibration velocity is approximately related to the distance between the monitoring point and blasting source, , and the maximum explosive weight per delay, . According to Safety Regulations for Blasting [17], the Sadaovsk empirical formula points out:
where is the maximum explosive weight per delay, is the distance between the monitoring point and blasting source, is proportional charge weight, is the blasting design and field geology coefficient, and a is the attenuation coefficient.
2.2. Hilbert-Huang transform
Hilbert-Huang transform is composed of Empirical Mode Decomposition (EMD) and Hilbert Spectrum Analysis (HSA). N. E. Huang believes that arbitrarily complicated signal can be composed of a series of Intrinsic Mode Function (IMF) which is simple, inharmonic and separate from each other. Hilbert-Huang transform was put forward based on above views and Empirical Mode Decomposition is the most important procedure of Hilbert-Huang transform [18].
Using Empirical Mode Decomposition, a raw signal can be expressed as follows [19]:
where is a raw signal; is intrinsic mode function and is residual error.
Using Hilbert-Huang transform for every intrinsic mode function :
where is Cauchy principal value, we can obtain analytic signal :
where is amplitude value function:
and is phase function:
Transient frequency is determined by derivation for phase function :
The amplitude and frequency derived from Hilbert-Huang transform is a function about time, by expressing the change of amplitude as frequency and time change, we can obtain Hilbert spectrum:
Hilbert energy spectrum is obtained from the time integration of the square of Hilbert spectrum amplitude :
Hilbert energy spectrumprovides an expression of energy calculation for every frequency and is defined as total energy accumulation in long-term span for every frequency.
In contrast with traditional Fourier transform using a series of harmonic wave to simulate vibration signal and Wavelet transform with the problem on selection of wavelet basis function, Hilbert-Huang transform has no constant and preset basis function and has better identifying ability in local region of blasting vibration signal.
2.3. Safety criterion of blasting vibration effect
Due to the complexity of blasting seismic wave propagation and the diversity of influencing factors, there are great differences in engineering standards for safety criterion of blasting seismic effect adopted at home and abroad [20, 21]. For rock and concrete materials, the dynamic tensile strength plays a major role in the safety and stability of the material itself and its structure under the blasting load. The dynamic tensile stress is proportional to the particle vibration velocity, thus the early safety criterion of blasting vibration effect is based on single peak vibration velocity to judge whether the structure and the building is safe or not, such as Longerfors [22], Edwards [23], Fogelson [24], Northwood [25] and Bollinger [26], etc. all taking single particle vibration velocity (or acceleration) as safety criterion.
With the development of the theory and technology for blasting engineering, the researchers found that the frequency and velocity both has great influence on the engineering facilities, using a single strength parameter as the basis of safety standards evaluation for blasting vibration has great limitation. In this way, for many countries, such as Germany, the United States, Switzerland and China, the vibration velocity and frequency are taken into account when the safety standards for blasting vibration are formulated.
According to the United States Bureau of Mines (USBM) and Office of Surface Mining Reclamation and Enforcement (OSMRE) in American [20], the safety criterion of USBM and OSMRE is shown in Fig. 1.
Fig. 1Safety criteria of USBM and OSMRE
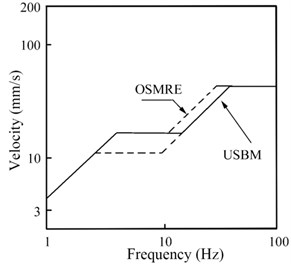
Table 1Safe allowable standards for blasting vibration
Sequence number | Object of protection | Allowable limit of particle vibration velocity (cm/s) | ||
10 Hz | 10 Hz 50 Hz | 50 Hz | ||
1 | Cave dwelling, adobe building and rubble building | 0.15-0.45 | 0.45-0.9 | 0.9-1.5 |
2 | Common civil building | 1.5-2.0 | 2.0-2.5 | 2.5-3.0 |
3 | Industrial building and commercial building | 2.5-3.5 | 3.5-4.5 | 4.2-5.0 |
4 | General ancient architecture and historic site | 0.1-0.2 | 0.2-0.3 | 0.3-0.5 |
5 | Central control room equipment at hydropower station and power plant in service | 0.5-0.6 | 0.6-0.7 | 0.7-0.9 |
6 | Hydraulic tunnel | 7-8 | 8-10 | 10-15 |
7 | Traffic tunnel | 10-12 | 12-15 | 15-20 |
8 | Mine tunnel | 15-18 | 18-25 | 20-30 |
9 | Permanently high rock slope | 5-9 | 8-12 | 10-15 |
10 | The new pouring mass concrete (C20): Curing time: initial solidification - 3d Curing time: 3d-7d Curing time: 7d-28d | 1.5-2.0 3.0-4.0 7.0-8.0 | 2.0-2.5 4.0-5.0 8.0-10.0 | 2.5-3.0 5.0-7.0 10.0-12 |
The “Safety regulations for blasting” (GB6722-2014) in China specified safety criterion of blasting vibration for the ground building, central control room equipment at hydropower station and power plant in service, hydraulic tunnel, traffic tunnel, mine tunnel, high rock slope and the new pouring mass concrete, etc. based on peak particle velocity and the main vibration frequency. Safe allowable standards for blasting vibration are listed in Table 1, for different protection object, the allowable limit of particle vibration velocity is different at diverse range of main vibration frequency. When the main vibration frequency is 10 Hz, 10 Hz 50 Hz and 50 Hz, respectively, for the common civil building, the allowable limit of particle vibration velocity is 1.5-2.0 cm/s, 2.0-2.5 cm/s and 2.5-3.0 cm/s, respectively; for the hydraulic tunnel, the safety criteria of particle vibration velocity is 7-8 cm/s, 8-10 cm/s and 10-15 cm/s, respectively. Besides, different control standards are adopted for new pouring mass concrete (C20) of varying ages, when the main vibration frequency is 10 Hz, 10 Hz 50 Hz and 50 Hz, respectively, for curing time between initial solidification and 3d, the allowable limit of particle vibration velocity is 1.5-2.0 cm/s, 2.0-2.5 cm/s and 2.5-3.0 cm/s, respectively; for curing time between 3d and 7d, the allowable limit of particle vibration velocity is 3.0-4.0 cm/s, 4.0-5.0 cm/s and 5.0-7.0 cm/s, respectively; for curing time between 7d and 28d, the allowable limit of particle vibration velocity is 7.0-8.0 cm/s, 8.0-10.0 cm/s and 10.0-12 cm/s, respectively.
3. Case study
3.1. Introduction to Taishan nuclear power station
The project, Taishan Nuclear Power Station, is located in Taishan city, the south of Guangdong Province, China. Its geographical location is at longitude 112° 59' E and latitude 21° 54' N, which is located to the east of the Huangmao Sea and is about 5 km from the southeast of Dajin Island. The project construction scale is preliminarily to 6×1750MW European pressurized water reactor (EPR) which will be divided into three phases and two EPR nuclear power units are planned in the first phase. According to the design requirements, the construction of the 0+000 to 0+200 m mileage section of the open channel for phase I of Taishan nuclear power station project requires the ground blasting and underwater reef blasting for rock excavation. The excavation of the rock is about 257361.35 m3, of which about 53954.25 m3 is excavated in land and about 203407.1 m3 is excavated in the submerged reef. The blasting site for rock excavation of open channel on land in Taishan is shown in Fig. 2.
Fig. 2The blasting site for rock excavation of open channel on land in Taishan

Because blasting stress wave in bedrock blasting excavation may give rise to damage for No. 1-No. 2 lock gate of water tunnel, it is necessary to carry out blast-induced damage control. The main purpose of monitoring is to validate the feasibility and the rationality of the blasting design parameters for blasting scheme and to correctly guide the construction using the attenuation law and time-frequency characteristics of monitoring results.
3.2. Monitoring and attenuation law for blasting vibration signal
Due to the TC-4850 blasting vibration monitoring system has the advantages of small size, light weight, high sensitivity and high automation, it is extraordinary suitable for the need of large quantities and long duration for rock blasting vibration monitoring. The field blasting vibration monitoring points are arranged in the near side of the open channel above the explosion zone, in which the attenuation law of blasting vibration signal for the lock gate is monitored by three vector sensors which can monitor horizontal radial, horizontal tangent and vertical direction at each measuring point during the blasting excavation. The blasting vibration monitoring system for bedrock excavation blasting and the layout of blasting vibration monitoring point of three vector sensor are shown in Fig. 3.
Fig. 3The blasting vibration monitoring system and layout of blasting vibration monitoring points

a) The blasting vibration monitoring system
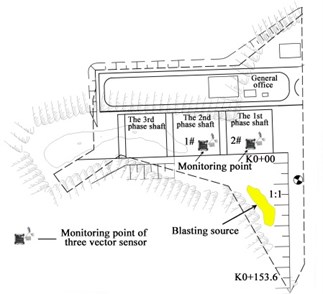
b) The layout of blasting vibration monitoring points
Table 2Parts of monitoring results of peak particle velocity under explosion
Maximum explosive weight per delay (kg) | Total explosive weight (kg) | Distance (m) | Horizontal radial direction | Horizontal tangential direction | Vertical direction | |||
(cm/s) | (Hz) | (cm/s) | (Hz) | (cm/s) | (Hz) | |||
96 | 240 | 225 | 1.11 | 15.6 | 0.17 | 25.0 | 0.82 | 17.5 |
108 | 336 | 122 | 0.78 | 21.5 | 0.73 | 29.8 | 1.01 | 22.9 |
108 | 408 | 106 | 0.91 | 25.6 | 0.92 | 41.7 | 0.67 | 19.6 |
110 | 984 | 54 | 3.00 | 10.7 | 2.01 | 40.0 | 4.70 | 19.0 |
144 | 768 | 184 | 0.73 | 17.2 | 0.38 | 18.9 | 0.70 | 15.9 |
150 | 960 | 210 | 0.80 | 13.9 | 0.28 | 14.7 | 0.79 | 58.8 |
150 | 1168 | 143 | 1.46 | 16.1 | 0.47 | 11.7 | 1.55 | 22.5 |
160 | 1392 | 47 | 3.98 | 16.3 | 3.11 | 33.2 | 9.43 | 47.4 |
180 | 768 | 191 | 0.52 | 12.5 | 0.51 | 10.8 | 0.18 | 12.5 |
190 | 816 | 145 | 1.43 | 16.1 | 0.54 | 45.9 | 2.11 | 46.4 |
188.5 | 1248 | 58 | 5.55 | 20.5 | 1.95 | 10.7 | 5.79 | 32.2 |
200 | 1176 | 51 | 4.16 | 7.30 | 3.09 | 11.2 | 9.64 | 69.8 |
200 | 1680 | 60 | 5.55 | 20.5 | 1.95 | 10.7 | 5.79 | 32.2 |
240 | 1576 | 64 | 2.72 | 21.6 | 2.73 | 24.6 | 2.84 | 29.7 |
240 | 1152 | 347 | 0.22 | 9.30 | 0.30 | 14.6 | 0.62 | 20.1 |
300 | 1968 | 96 | 1.81 | 10.7 | 1.65 | 25.9 | 3.54 | 34.2 |
300 | 2904 | 362 | 0.51 | 15.6 | 0.18 | 15.6 | 0.74 | 46.9 |
340 | 1080 | 91 | 2.03 | 11.2 | 1.89 | 10.7 | 4.19 | 17.1 |
350 | 1248 | 147 | 1.25 | 17.1 | 0.87 | 11.7 | 2.06 | 16.6 |
450 | 1080 | 114 | 4.14 | 32.3 | 1.09 | 40.0 | 3.84 | 21.7 |
800 | 1608 | 114 | 3.84 | 26.3 | 1.56 | 27.0 | 2.83 | 23.8 |
Altogether 168 blasting vibration data along the horizontal radial, horizontal tangential and vertical direction were recorded from 56 blasts. Parts of monitoring results of peak particle velocity under explosion are shown in Table 2.
Total 123 blasting vibration data from 41 blasts from controlled blasting and bench blasting are selected to fit in the form of power function based on Eq. (4) for bedrock excavation blasting. The regression analysis results of peak particle velocity along the horizontal radial, horizontal tangential and vertical direction are shown in Fig. 4.
Fig. 4The regression analysis of blast vibration velocity, ν, and the proportional charge weight, ρ
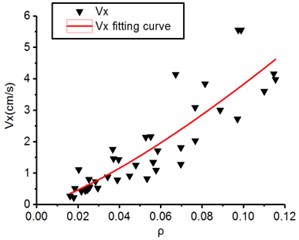
a) Horizontal radial direction
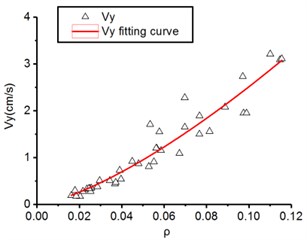
b) Horizontal tangential direction
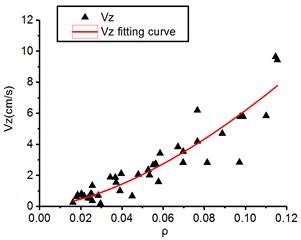
c) Vertical direction
The Sadaovsk empirical formula on regressive analysis along the horizontal radial, horizontal tangential and vertical direction is expressed as Eqs. (13-15), respectively:
The blast-induced wave propagation law is obtained in the form of Eqs. (13-15), based on the above equation, we can effectively present the blasting design about the maximum explosive weight per delay, , according to the allowable peak particle velocity, , at different distance from the explosion source, , in terms of requisition of “Safety regulations for blasting” (GB6722-2014) in China, which shows the excellent control effect on blasting damage of the lock gate and surrounding rock mass.
It is observed in Eqs. (13-15) that the range of variation for is from 63.2 to 241.8 and is from 1.31 to 1.56 that belongs to the range of medium and hard rock, which is consistent with the previous exploration of formation lithology, where it has been observed that , of vertical direction is largest, this is, 241.8 and 1.56, respectively but , of horizontal radial direction is 77.3 and 1.31, respectively and , of horizontal tangential is 63.2 and 1.40, respectively.
In term of Sadaovsk empirical formula in Eq. (4), parameter is directly proportional to particle vibration velocity and parameter represent attenuation speed of particle vibration velocity where the bigger of , the faster of velocity attenuation along propagation distance. By comparing the difference of and for horizontal radial, horizontal tangential and vertical direction, we easily find that the of vertical direction is more than horizontal radial and horizontal tangential direction while of vertical direction is also more than horizontal radial and horizontal tangential direction which show that vertical direction has faster speed of velocity attenuation, it imply that even though peak particle velocity of vertical direction is generally larger than horizontal radial and horizontal tangential direction in the near field of blasting source, however, the peak particle velocity of vertical direction will be lower than horizontal radial and horizontal tangential direction in the far field of blasting source which is consistent with the results shown in Table 2. So, it is noteworthy that we should take three different direction components of particle vibration velocity rather than single direction into account as safety criteria for blasting vibration.
3.3. Time-frequency characteristics for blasting vibration signal
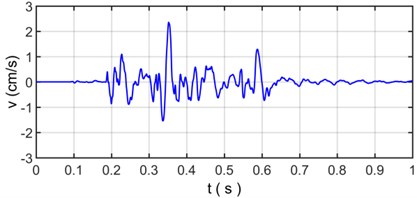
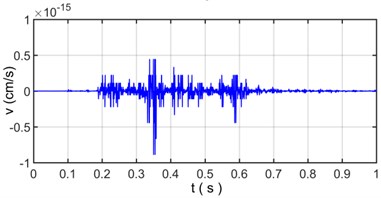
As seen in Fig. 5, there is a typical multiple section raw signal of blasting seismic wave. The sampling points are 2000 and sampling interval time is 0.0005 s. The original vibration signal (Fig. 5) is decomposed and reconstructed by Empirical Mode Decomposition, the decomposed vibration signal is shown in Fig. 6 and the reconstructed vibration signal and relative error are shown in Fig. 7.
Fig. 5The blasting site for rock excavation of open channel on land in Taishan
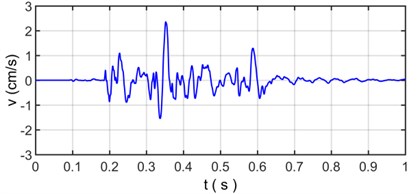
Fig. 6 shows that the original vibration signal is decomposed into 9 intrinsic mode functions from c1 to c8 and for residual error. Because Empirical Mode Decomposition always decompose raw vibration signal based on time scales from big to small, the waveform of intrinsic mode functions are becoming more and more longer while the frequency is becoming more and more lower with the proceed of decomposition. The intrinsic mode functions commonly have distinctly physical implication: The c1 component has the highest frequency and the energy is very small, which indicates that it is usually considered to be a high frequency noise that needs to be denoised in the process of analysis on frequency spectrum characteristics for blasting vibration signal. The c2, c3, c4, c5 and c6 component have larger amplitude than other intrinsic mode functions and contain a majority of energy of original vibration signal which become main component to influence of building vibration; the c7 and c8 component have less frequency, amplitude and energy of original vibration signal coming from resident signal or other factors. Residual error R reflects the zero-drift phenomenon or weak change tendency of signal with the lowest amplitude and energy.
As is shown in Fig. 7, the reconstructed vibration signal based on Empirical Mode Decomposition is very consistently similar to original vibration signal with relative error is within in 10-15, which shows that Hilbert-Huang transform, and Empirical Mode Decomposition can accurately reflect the characteristics of the non-stationary signal and have an excellent suitability for analysis on blasting vibration signal.
Fig. 8 shows power spectrum density of original vibration signal (Fig. 5) and Fig. 9 shows power spectrum density of intrinsic mode functions from c1 to c8 and (Fig. 6).
Fig. 6The decomposed vibration signal by empirical mode decomposition
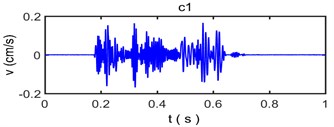
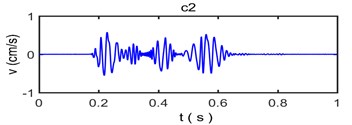
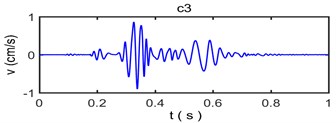
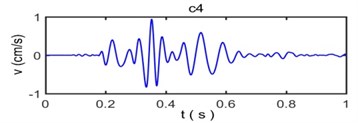
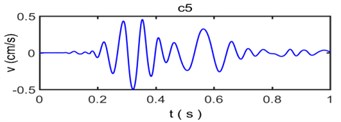
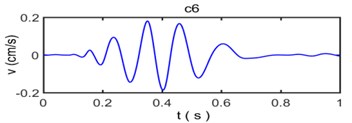
Fig. 7The reconstruction of signal and relative error based on empirical mode decomposition
a) Reconstruction signal based on empirical mode decomposition
b) Relative error based on empirical mode decomposition
Fig. 8 indicates the blast energy of original vibration signal mainly concentrate on the region where frequency is below 80 Hz and has three sub-band which varies from 10 Hz to 18 Hz, from 22 Hz to 45 Hz and from 50 Hz to 80 Hz, respectively, in which the main energy concentrates in the range of 10 Hz to 45 Hz, and the energy in the range of 50 Hz to 80 Hz is relatively weak and uniformly distributed. The natural frequencies of common lock gate are between 2 Hz and 5 Hz, from the perspective of security, low energy distribution in the low frequency region is beneficial to structural safety and stability of surrounding rock mass for reducing the probability of resonance [11, 27].
Fig. 8The power spectral density of original blasting vibration signal
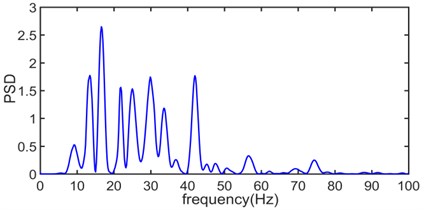
Fig. 9The power spectral density of IMF component from c1 to c8 and R as surplus
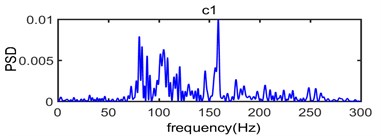
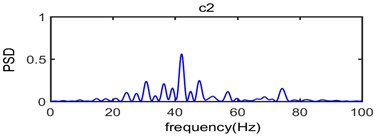
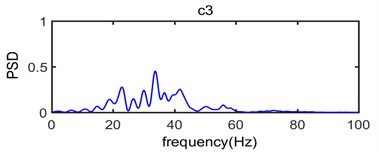
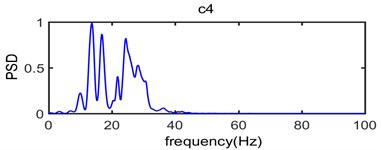
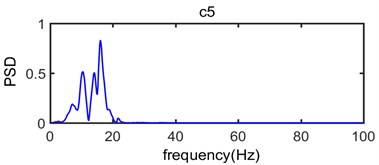
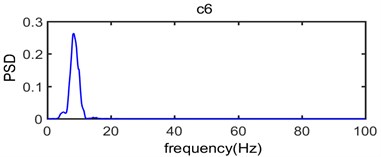
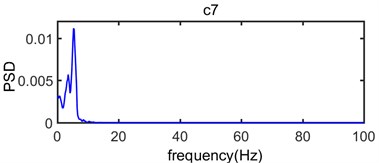
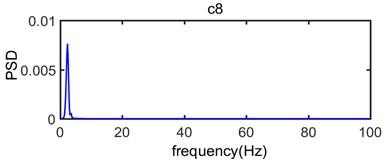
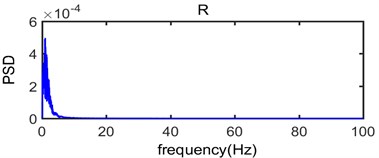
As seen in Fig. 9, the c1 component is usually considered to be high frequency noise signal, it has very small power spectral density value while the range of frequency distribution is wide which mainly vary from 70 Hz to 270 Hz; In the process of analysis on the original signal, the c1 component should be removed in order to eliminate the effect of high frequency noise. In terms of the main components of the original vibration signal c2, c3, c4, c5 and c6 component, the dominant frequency distribution range mainly vary from 30 Hz to 80 Hz, from 10 Hz to 50 Hz, from 10 Hz to 40 Hz, from 5 Hz to 20 Hz and from 5 Hz to 12 Hz, respectively; In addition, the power spectral density value of c7, c8 and is very small which corresponding dominant frequency distribution range is below 7 Hz. Thus, it can be seen that the spectrum of intrinsic mode functions signal is abundant which can be divided into multiple sub-seismic frequency bands and most of them are below 80 Hz; This is consistent with the power spectrum density of original vibration signal shown in Fig. 8 where the dominant frequency of the original vibration signal is mainly in the range of 10 Hz-80 Hz.
The three-dimensional energy density spectrum of original vibration signal on Hilbert-Huang transform is shown in Fig. 10.
Fig. 10The three-dimensional energy density spectrum based on Hilbert-Huang transform
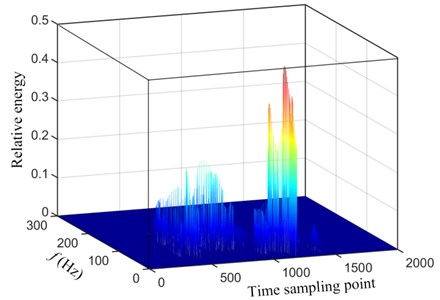
Fig. 10 presented the distribution characteristics about energy of blasting vibration signal as the variation of frequency and time; It can be more intuitive to show the distribution of energy on blasting vibration signal with time and frequency, where the color is redder, the energy is greater; We can clearly see that most of the energy distribution in the frequency range is below 100 Hz, in which the energy distribution frequency band higher than 100 Hz is very small, the energy mainly concentrates on the range of 10 Hz-80 Hz and 360-1250 time sampling point. Dividing time sampling point 360-1250 by sampling frequency 2000 Hz is 0.180 s-0.625 s, we can obtain the energy mainly concentrates on the scope of 10 Hz-80 Hz and 0.180 s-0.625 s. The distribution characteristics about energy density spectrum of original vibration signal based on Hilbert-Huang transform is in accordance with the velocity curve of original vibration signal in Fig. 5 where the time region for velocity vibration amplitude mainly vary from 0.180 s to 0.625 s and the power spectral density of original vibration signal in Fig. 8 where the frequency region for power spectral density mainly concentrate on 10 Hz-80 Hz.
3.4. Initiative control for blasting vibration effect
Blasting vibration effect is affected by the topography, geology and blasting design parameters. To reduce the blasting vibration effect, the corresponding measure should be taken into account with different perspectives, which mainly can be divided into millisecond delay blasting technology, controlling maximum explosive weight per delay and total explosive weight, choosing right powder factor and rational spacing pattern parameter, improving terrain condition by ditch excavation and presplitting blasting technology.
In this paper, the initiative control for blasting vibration effect is mainly by controlling maximum explosive weight per delay and total explosive weight. As seen in the Table 2, in terms of the peak particle velocity of 21 groups monitoring data, the vertical direction is generally greater than horizontal radial and horizontal tangential direction in the near field of blasting source and the peak particle velocity of vertical direction is usually lower than horizontal radial and horizontal tangential direction in the far field of blasting source. Therefore, it is noteworthy that we should take three different direction components of particle vibration velocity rather than single direction into account as safety criteria for blasting vibration. “Safety regulations for blasting” (GB6722-2014) points out the allowable particle vibration velocity is subject to the maximum value of three mutually perpendicular components in cartesian coordinate of blasting vibration signal and the vibration frequency is the main vibration frequency of allowable particle vibration velocity. Because the lock gate belongs to new pouring mass concrete with concrete strength grade of C50 and curing time has been over 28 days at the start of blasting for bedrock excavation on land for open channel project; meanwhile, as for the measured vibration data, the main vibration frequency of the blasting vibration signal is mainly in 10 Hz-80 Hz, the initiative control standard of particle vibration velocity is determined to [V] = 5.0 cm/s according to Table 1 of “Safety regulations for blasting” [17] and expert opinion [28].
Table 3The maximum explosive weight per delay calculated by Eq. (13) to Eq. (15)
Blast radial distance (m) | Horizontal radial direction | Horizontal tangential direction | Vertical direction | Maximum explosive weight per delay (kg) |
(kg) | (kg) | (kg) | ||
10 | 1.9 | 4.4 | 0.6 | 0.6 |
20 | 15.1 | 34.9 | 4.6 | 4.6 |
30 | 51.0 | 117.6 | 15.6 | 15.6 |
40 | 121.0 | 278.8 | 36.9 | 36.9 |
50 | 236.3 | 544.5 | 72.0 | 72.0 |
60 | 408.4 | 940.9 | 124.5 | 124.5 |
70 | 648.5 | 1494.2 | 197.7 | 197.7 |
80 | 968.0 | 2230.4 | 295.0 | 295.0 |
90 | 1378.3 | 3175.7 | 420.1 | 420.1 |
100 | 1890.7 | 4356.3 | 576.2 | 576.2 |
110 | 2516.5 | 5798.2 | 766.9 | 766.9 |
120 | 3267.1 | 7527.6 | 995.7 | 995.7 |
Due to the phenomenon about field monitoring particle vibration velocity more than initiative control standard of particle vibration velocity is existed, therefore, we should control maximum explosive weight per delay at different distance from the explosion source on the basis of the blast-induced wave propagation law based on Eq. (13), Eq. (14) and Eq. (15). As shown in Table 3 above, the allowable maximum explosive weight per delay is controlled by maximum explosive weight per delay of vertical direction. Supposing the distance between lock gate monitoring point and the explosion source is 50 m, the maximum explosive weight per delay can be evaluated to 72 kg; that is, it can satisfy the lock gate concrete structure safety when the maximum explosive weight per delay dose not greater than 72 kg. In order to guarantee safety of damage control for lock gate and surrounding rock mass under blasting load in Taishan Nuclear Power Station, it is essential that we should strictly control maximum explosive weight per delay and total explosive weight based on above calculation results of Table 3. In the subsequent process of rock blasting, we have achieved excellent effect on blasting control. Summary of experimental blasts details at open channel in Taishan nuclear power station is given in Table 4.
Table 4Summary of blasts details at open channel in Taishan nuclear power station
No. of blasts | Diameter of hole (mm) | Burden (m) | Spacing (m) | Depth of blast hole (m) | Length of stemming (m) | Total charge (kg) | Maximum charge per delay(kg) | Initiation systems | Explosives |
56 | 150 | 3-3.5 | 3-3.5 | 2-11 | 1-4 | 120-2904 | 36-800 | Non-electric shock tube delay detonator and milli-second connector | Emulsion explosive |
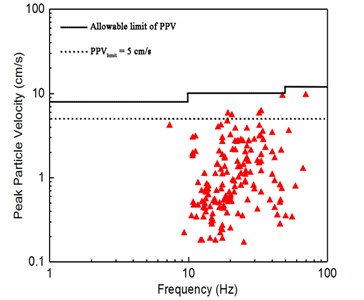
The measured magnitudes of peak particle velocity and frequency of the 168 blasting vibration data along the horizontal radial, horizontal tangential and vertical direction from 56 blasts were evaluated taking into consideration the established damage criteria of the “Safety regulations for blasting” (GB6722-2014) in China; As required in Table 1, in view of the lock gate belongs to new pouring mass concrete with concrete strength grade of C50 and curing time has been over 28 days at the start of blasting for bedrock excavation for open channel project, the safety criteria of particle vibration velocity for lock gate could be set as 8 cm/s, 10 cm/s and 12 cm/s, respectively when the main vibration frequency is 10 Hz, 10 Hz 50 Hz and 50 Hz, respectively. The evaluation of damage risk of the blasts on lock gate according to “Safety regulations for blasting” in China is shown in Fig. 11.
It was observed in Fig. 11 that a major part of the recorded peak particle velocity were below the initiative control standard of particle vibration velocity [V] = 5.0 cm/s and the PPV values versus different frequency for all blasts were below allowable limit of PPV for new pouring mass concrete with curing time over 28d described in the safety criteria of “Safety regulations for blasting” in China. This work could be conducive to future design of similar blasting engineering about lock gate damage control.
Fig. 11Evaluation of damage risk of the blasts on lock gate according to “Safety regulations for blasting”
4. Conclusions
This paper presents the attenuation law and time-frequency characteristics of blasting vibration signal of open channel in Taishan Nuclear Power, At the same time, the initiative control measure for blasting vibration effect is carried out by controlling maximum explosive weight per delay in advance, the main conclusions of the study are drawn as follows:
1) The Sadaovsk empirical formula on regressive analysis along the horizontal radial, horizontal tangential and vertical direction is expressed as, , respectively. In terms of the peak particle velocity of monitoring data, the vertical direction is generally greater than horizontal radial and horizontal tangential direction in the near field of blasting source and the peak particle velocity of vertical direction is usually lower than horizontal radial and horizontal tangential direction in the far field of blasting source; therefore, it is noteworthy that we should take three different direction components of particle vibration velocity rather than single direction into account as safety criteria for blasting vibration.
2) As for those monitoring data, the blasting vibration signal is analyzed by Empirical Mode Decomposition based on Hilbert-Huang transform which is decomposed into 9 intrinsic mode functions from c1 to c8 and R for residual error within the range of 10-15. The three-dimensional energy density spectrum show the energy mainly concentrates on the scope of 10 Hz-80 Hz and 0.180 s-0.625 s that is in accordance with the velocity curve of original vibration signal where the time region for velocity vibration amplitude mainly vary from 0.180 s to 0.625 s and the power spectral density of original vibration signal where the frequency region for power spectral density mainly concentrate on 10 Hz-80 Hz, which is much higher than natural frequency of lock gate and is beneficial to structural safety and stability of surrounding rock mass for reducing the probability of resonance.
(3) The initiative control standard of particle vibration velocity is determined to [V] = 5.0 cm/s according to “Safety regulations for blasting” and expert opinion, a major part of the recorded peak particle velocity were below the initiative control standard of particle vibration velocity [V] = 5.0 cm/s and the PPV values versus different frequency for all blasts were below allowable limit of PPV for new pouring mass concrete with curing time over 28d described in the safety criteria of “Safety regulations for blasting” in China; We have controlled maximum explosive weight per delay at different distance from the explosion source on the basis of the blast-induced wave propagation law in the form of Sadaovsk empirical formula, In the subsequent process of rock blasting, it shown excellent effect on blasting damage control for lock gate and surrounding rock mass.
References
-
Zhang X. L., Huang S. T. Blasting Seismic Effect. Seismological Press, Beijing, 1981.
-
Li Y. Q., Ma S. Z. Explosion Mechanics. Science and Technology Press, Beijing, 1992.
-
Feng S. Y., Lv Y., Gu Y. C. City Control Blasting. China Rail Press, Beijing, 1996.
-
Liu D. Z. Practical Manual for Blasting Engineering. Metallurgical Industry Press, Beijing, 2003.
-
Wei X. L., Zheng B. X. Destructive effect of blasting vibration on nearby structures. Engineering Blasting, Vol. 6, Issue 3, 2000, p. 81-88.
-
Wang C., Gao C. Blasting vibration monitoring and controlling of underground excavation of light rail station in city. Chinese Journal of Underground Space and Engineering, Vol. 7, Issue 2, 2011, p. 1688-1691.
-
Jiang Y. G., Shen Z. W., Yang C. D. Big charge blasting vibration damping and vibration monitoring analysis under intracity complicated environment. Journal of Vibration and Shock, Vol. 31, Issue 1, 2012, p. 156-161.
-
Lin C. M., Chen L. B., Jiang L. L., et al. Research on blasting stability control technology of large-span highway tunnel with super-small clear spacing at highway expansion project. Chinese Journal of Rock Mechanics and Engineering, Vol. 29, Issue 7, 2010, p. 1371-1378.
-
Zeng S., Yang S. J., Tan K. X., et al. Experimental research into effect of blasting vibration on stability of surface buildings. Journal of Mining and Safety Engineering, Vol. 25, Issue 2, 2008, p. 176-179.
-
Wang H. B., Zong Q. Study of blasting vibration character of soft rock roadway excavation in coalmine. Chinese Journal of Rock Mechanics and Engineering, Vol. 31, Issue 2, 2012, p. 3876-3881.
-
Zong Q., Wang H. B., Xu Y., et al. Analysis of blasting seismic wave signal in coalmine roadway excavation based on HHT method. Journal of Vibration and Shock, Vol. 32, Issue 15, 2013, p. 116-120.
-
Huo Y. J. Blasting vibration effects on structures and safety analysis. Blasting, Vol. 20, Issue 1, 2003, p. 1-6.
-
Xu X. S. Blasting safety technologies in the circumstance of cross tunnels with small interval. Industrial Safety and Environmental Protection, Vol. 36, Issue 12, 2010, p. 36-37.
-
Jiang D. Y., Chen Y., et al. Blasting vibration monitoring and control technology of super small clear distance cross tunnel. West-China Exploration Engineering, Vol. 20, Issue 10, 2008, p. 188-191.
-
Zong Q., Wang H. B., Zhou S. B. Research on monitoring and controlling techniques considering effects of seismic shock. Chinese Journal of Rock Mechanics and Engineering, Vol. 27, Issue 5, 2008, p. 938-945.
-
Lu W. B., Li H. B., Chen M., et al. Safety criteria of blasting vibration in hydropower engineering and several key problems in their application. Chinese Journal of Rock Mechanics and Engineering, Vol. 28, Issue 8, 2009, p. 1513-1520.
-
GB6722-2014. Safety Regulations for Blasting. The National Standards Compilation Group of People’s Republic of China. Standards Press of China, Beijing, China, 2014.
-
Semion K., Thomas Flatley P., et al. On the Hilbert-Huang Transform Data Processing System Development. National Aeronautics and Space Administration Goddard Space Flight Center, Darrell Smith Orbital Sciences Corporation, 2001.
-
Huang N. E., Shen Z., Long S. R., et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society of London, Vol. 5, Issue 4, 1998, p. 903-995.
-
Yan Z. X., Wang Y. H., Jiang P., et al. Study on measurement of blast-induced seism and building safety criteria. Chinese Journal of Rock Mechanics and Engineering, Vol. 22, Issue 11, 2003, p. 1907-1911.
-
Wang X. G., Yu Y. L. On several problems of safety criterion of blasting vibration. Engineering Blasting, Vol. 7, Issue 2, 2001, p. 88-92.
-
Langefors U., Kihlstrom B., Westerberg H. Ground vibration in blasting. Water Power, 1958, p. 335-421.
-
Edwards A. T., Northwood T. D. Experimental studies of the effects of blasting on structures. Engineer, Vol. 210, 1960, p. 538-546.
-
Duvalland W. I., Fogelson D. E. Review of Criteria for Estimating Damage to Residences from Blasting Vibration. US Bureau of Mines Report Investigation, Washington, 1962, p. 59-68.
-
Northwood T. D. Blasting vibrations and building damage. Engineer, Vol. 215, 1963, p. 973-978.
-
Bolinger G A. Blasting Vibration Analysis. Science and Technology Press, Beijing, 1975.
-
Li X. B., Ling T. H., Zhang Y. P. Analysis of Blast Vibration Signals Theories and Methods. Science Press, Beijing, 2009.
-
Lin J. H. Blast vibration safety and controlling in water intake area of the second phase of Jiulong River north-diversion project. China Rural Water and Hydropower, Vol. 53, Issue 2, 2011, p. 91-93.
About this article
The authors are very grateful to the editor and unknown referees for suggestions which improved the quality of this paper. In addition, the study is supported by the Key Program of National Natural Science Foundation of China under Grant No. 51439008, National Natural Science Foundation of China under Grant No. 41572307 and National Natural Science Funds for Distinguished Young Scholar of China under Grant No. 41525009.
Haibo Li contributed to the conception and design of the study. Xiang Xia and Yaqun Liu contributed significantly to analysis and manuscript preparation; Dr. Zeng performed the data analyses and wrote the manuscript; Hong Zuo and Jinlin Jiang helped perform the analysis with constructive discussions.
