A method for considering a distributed spring constant for studying the flexural vibration of an Euler-beam with lightweight multistage local resonators

1. Introduction

Phononic crystals (PCs) are artificial composite materials with periodic structure and elastic wave band gaps characteristics. The band gap characteristic is that the propagation of elastic waves is suppressed in the frequency range of band gap. In 1992, Sigalas et al. theoretically confirmed the existence of the elastic wave band gap for the first time [1]. The concept of PCs was then formally confirmed in 1993 [2]. Since then, more extensive researches have been carried out on PCs. And further development of PCs has offered new ideas on how to control wave propagation [3-8]. Generally, there are two types of mechanism for PCs: the Bragg scattering [9-13] and locally resonant (LR) mechanisms [14-19]. A considerable amount of research has been carried out on the Bragg band gap. However, since the wavelength corresponding to gaps of the Bragg scattering mechanism has the same order of magnitude as the lattice constant, it is difficult to obtain low-frequency gaps under the small-sized structure conditions [20-24]. The size limitation was broken when Liu et al. first proposed the LR mechanism [25]. The wavelength of the LR gap is considerably larger than the lattice constant, and a larger wavelength can be realized by employing a small-sized structure. Thus, possibilities are created for the application of PCs for low-frequency vibration.

Based on the concept of LR PCs, the one-stage LR structure periodically arranged on a beam, rod, and shaft, have been investigated, and the desirable low-frequency band gap has been obtained [26-28]. Yu et al. investigated the flexural vibration band gaps in the beam with one-stage local resonator [26]. Liu et al. discussed the frequency range and attenuation coefficient of the LR gap with different local resonators [28]. However, for the traditional LR beams there always attached the one-stage local resonator (one rubber ring covered by one scattering ring) and result that the lower band gap the heavier the scattering ring, which limit the application potential in engineering. Furthermore, the traditional one-stage structure commonly have only one band gap in the lower frequency range and is not proper to be applied in the multiple frequency ranges vibrations control. In recent years, multi-oscillators LR structures have also been designed, and the multiple low-frequency band gaps have been obtained [29-32]. Wen et al. presented a one-dimensional phononic crystals beam with multi-oscillators, studied its LR gap and found that it had a wider and richer vibration band gap than the one-stage LR structure [31]. Similarly, Wang et al. proposed a Timoshenko beam with periodically attached multi-oscillators, investigated the band gaps under flexural vibration and found that the lower band gap and frequency range could be obtained by using the multi-oscillators LR structure [32]. However, the density of the scattering layer in previous studies were all higher and have difficulty to be applied in engineering. In the previous studies the effects of the density of the scattering on the band gap were neglected, which determined the weight of the resonators in the LR structure. Therefore, in order to reduce the total structural weight this paper design a kind of the LR Euler beam periodically arranged lightweight LR multilayer rings (with two rubber rings and two scattering rings arranged alternately) and study its propagation characteristics of the flexible wave.

The transfer matrix (TM) [26, 28, 31, 33] and lumped mass (LM) methods [34, 35] are widely used to calculate the band gaps of one-dimensional PCs. Using the TM method, Liu et al. investigated band gaps during flexural vibration of a one-stage local resonator beam [28]. However, there is no appropriate and convenient theoretical method to study the band gap of the lightweight LR structure. When the scattering layer is lightweight, the rubber layer not only acts as a spring but also participates as the mass in the local resonance. For the traditional transfer matrix method, the mass of the rubber layer is neglected, and there is a distinct difference between the theoretical and simulation results as the density of scattering decreases. With the introduction of the LM method, Wen et al. proposed a method to investigate band gaps of one-dimensional multi-component PCs based on the LM method, which decreased the negative impact of sharp variations in elastic constants on the convergence of the structural calculation [34]. Based on LM theory, a continuous system can be discretized into a number of concentrated masses. However, this greatly increases the number of calculations. Therefore, this paper presents an improved transfer matrix method based on the idea of lumped mass method to study the lightweight multistage LR structure, which takes into account the mass of the rubber and requires less computation.

The paper is organized as follows. Section 2 describes the method for calculating flexural vibration band gaps in an Euler beam with periodically arranged lightweight multistage local resonators. The band gap of the one-stage locally resonant structure in [28] is calculated by the proposed method to verify the accuracy of the present method, and moreover, the convergence of the method is analyzed. In part three, the band gap characteristics of the lightweight multistage LR structure are calculated by the proposed method. And the frequency response function of the lightweight multistage LR structure is calculated by the finite element method. In Section 4, a simplified model for calculating the beginning frequency of the lightweight multistage LR structure is proposed and the influence of the scattering density on the precision of the simplified model is further analyzed. Some conclusions are provided in Section 5.

2. The transfer matrix method for considering a distributed spring constant

2.1. Analytical model

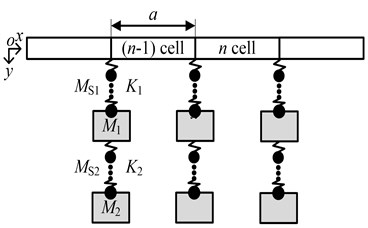
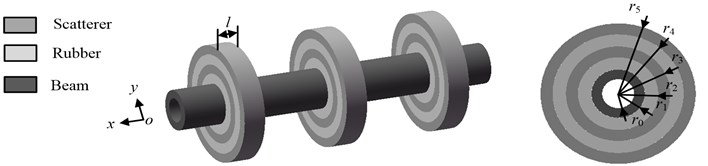
An analytical model of an Euler beam is presented in figure 1, in which lightweight multistage local resonators are periodically arranged. Each local resonator consists of a spring with a uniform mass and a mass block. The spring with a uniform mass represents the rubber, and the mass block represents the lightweight scattering. The mass of the first-stage and second-stage rubber is $M_{S1}$ and $M_{S2}$, respectively with respective radial stiffness $K_1$ and $K_2$. Furthermore, the mass of the first-stage and second-stage lightweight scattering is $M_1$ and $M_2$, respectively. The length of the beam between the adjacent resonators is $a$. Only transverse displacements are assumed to occur. The transverse displacement $y\left(x,t\right)$ of the Euler beam satisfies the following flexural vibration equation [28]:

1

$EI\frac{{\partial }^{4}y\left(x,t\right)}{\partial x^4}+\rho A\frac{{\partial }^{2}y\left(x,t\right)}{\partial t^2}=0,$

where, $E$ and $\rho$ are the Young’s modulus and density of the beam material, respectively. $I$ is the moment of inertia with respect to the axis perpendicular to the beam axis; $A$ is the cross-section area of the beam. $y\left(x,t\right)$ is the dynamic displacement at $x$. Considering the normal-mode condition, $y\left(x,t\right)$ can be written as $y(x,t)=X\left(x\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(i\omega t\right)$, where $\omega$ is the circular frequency.

Fig. 1The analytical model of an Euler beam with periodically attached lightweight multistage local resonators

For the $n$th cell, the solution of Eq. (1) can be written as [28]:

2

$y\left(x_n^{\mathrm{\text{'}}},t\right)=e^{i\omega t}\left[A_n\mathrm{c}\mathrm{o}\mathrm{s}\left(\alpha x_n^{\mathrm{\text{'}}}\right)+B_n\mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha x_n^{\mathrm{\text{'}}}\right)+C_n\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}\left(\alpha x_n^{\mathrm{\text{'}}}\right)+D_n\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{h}\left(\alpha x_n^{\mathrm{\text{'}}}\right)\right],$

here:

${\alpha }^4=\frac{\rho A{\omega }^2}{EI},x^{\mathrm{\text{'}}}=x-na.$

As shown in Fig. 1, in the transfer matrix method for considering a distributed spring constant, the first-stage and second-stage rubber with a continuously distributed mass are divided into $N_1$ and $N_2$ lumped masses, respectively, and the mass of the rubber is evenly distributed in each lumped mass. The $N_1$ and $N_2$ lumped masses are connected by springs, $N_1$ and $N_2$, and discretely distributed at the lower ends of the spring. The $N_1$th lumped mass of the first-stage rubber and the $N_2$th lumped mass of the second-stage rubber are attached to the first-stage scattering and second-stage scattering, respectively. The radial stiffness of each rubber is considered equivalent to the coefficient of stiffness of $N_1$ and $N_2$ springs, respectively, which are connected in series. Therefore, a unit cell having the lightweight multistage LR structure can be simplified to $N\left(N=N_1+N_2\right)$ mass-spring systems connected in series.

The spring $k_i$ of the $i$th mass-spring is given as:

3

$k_i=\left\{\begin{array}{ll}{N}_1\cdot K_1& i=\left(\mathrm{1,2},...,N_1\right),\\ N_2\cdot K_2& i=\left(N_1+1,N_1+2,...,N_1+N_2\right).\end{array}\right.$

Furthermore, the lumped mass $m_i$ of the $i$th mass-spring can be written as:

4

$m_i=\left\{\begin{array}{ll}\frac{M_{S1}}{N_1},i=\left(\mathrm{1,2},...,N_1-1\right),& \\ \frac{M_{S1}}{N_1}+M_1,i=\left(N_1\right),& \\ \frac{M_{S2}}{N_2},i=\left(N_1+1,N_1+2,...,N_1+N_2-1\right),& \\ \frac{M_{S2}}{N_2}+M_2,i=\left(N_1+N_2\right).& \end{array}\right.$

The displacement in the $i$th mass-spring for the $n$th unit cell is given by $Z_{ni}\left(t\right)=V_{ni}\mathrm{e}\mathrm{x}\mathrm{p}\left(i\omega t\right)$, where $V_n$ is the amplitude of its vibration. For the first mass-spring, $i$th ($i=$ 2, 3, ..., $N$-1) mass-spring, and $N$th mass-spring, the motion equations are given by:

5

$m_1\frac{{\partial }^2{Z}_{n1}\left(t\right)}{\partial t^2}+k_1\left(Z_{n1}\right(t)-y_n(0,t\left)\right)-k_2\left(Z_{n2}\right(t)-Z_{n1}(t\left)\right)=0,$

6

$m_i\frac{{\partial }^2{Z}_{ni}\left(t\right)}{\partial t^2}+k_i\left(Z_{ni}\right(t)-Z_{n\left(i-1\right)}(t\left)\right)-k_{\left(i+1\right)}\left(Z_{n\left(i+1\right)}\right(t)-Z_{ni}(t\left)\right)=0,$

7

$m_N\frac{{\partial }^2{Z}_{nN}\left(t\right)}{\partial t^2}+k_N\left(Z_{nN}\right(t)-Z_{n\left(N-1\right)}(t\left)\right)=0.$

From Eqs. (2), (5), (6) and (7), the relationship between $V_{n1}$ and $X_n\left(0\right)$ can be defined as:

8

$V_{n1}=\frac{k_1{X}_n\left(0\right)+k_2{V}_{n2}}{k_1-m_1{\omega }^2+k_2},$

where:

$V_{n2}=\frac{k_2{V}_{n1}+k_3{V}_{n3}}{k_2-m_2{\omega }^2+k_3},V_{ni}=\frac{k_i{V}_{n(i-1)}+k_{i+1}{V}_{n(i+1)}}{k_i-m_i{\omega }^2+k_{i+1}},V_N=\frac{k_N{V}_{N-1}}{k_N-m_N{\omega }^2}.$

The continuities of the displacement, slope, bending moment, and shear force at the interface between the ($n-1$)th and $n$th unit cell [28] give:

9

$A_n+C_n=A_{n-1}\mathrm{c}\mathrm{o}\mathrm{s}\left(\alpha a\right)+B_{n-1}\mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha a\right)+C_{n-1}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}\left(\alpha a\right)+D_{n-1}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{h}\left(\alpha a\right),$

10

$A_n+C_n=A_{n-1}\mathrm{c}\mathrm{o}\mathrm{s}\left(\alpha a\right)+B_{n-1}\mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha a\right)+C_{n-1}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}\left(\alpha a\right)+D_{n-1}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{h}\left(\alpha a\right),$

11

$-A_n+C_n=-A_{n-1}\mathrm{c}\mathrm{o}\mathrm{s}\left(\alpha a\right)-B_{n-1}\mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha a\right)+C_{n-1}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}\left(\alpha a\right)+D_{n-1}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{h}\left(\alpha a\right),$

12

$F-B_n+F+D_n=A_{n-1}\mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha a\right)-B_{n-1}\mathrm{c}\mathrm{o}\mathrm{s}\left(\alpha a\right)+C_{n-1}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{h}\left(\alpha a\right)+D_{n-1}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}\left(\alpha a\right),$

where:

$F=\frac{-k_1(V_{n1}-X_n(0\left)\right)}{EI{\alpha }^3}.$

Thus, Eqs. (9)-(12) can be written in matrix form as:

13

$\mathbf{K}{\mathbf{\varphi }}_n=\mathbf{H}{\mathbf{\varphi }}_{n-1},$

where:

${\mathbf{\varphi }}_n=[A_n,B_n,C_n,D_n{]}^T,\mathbf{}\mathbf{}\mathbf{}\mathbf{K}=\left[\begin{array}{cccc}1& 0& 1& 0\\ 0& 1& 0& 1\\ -1& 0& 1& 0\\ F& -1& F& 1\end{array}\right],$
$\mathbf{H}=\left[\begin{array}{cccc}\mathrm{c}\mathrm{o}\mathrm{s}\left(\alpha a\right)& \mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha a\right)& \mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}\left(\alpha a\right)& \mathrm{s}\mathrm{i}\mathrm{n}\mathrm{h}\left(\alpha a\right)\\ -\mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha a\right)& \mathrm{c}\mathrm{o}\mathrm{s}\left(\alpha a\right)& \mathrm{s}\mathrm{i}\mathrm{n}\mathrm{h}\left(\alpha a\right)& \mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}\left(\alpha a\right)\\ -\mathrm{c}\mathrm{o}\mathrm{s}\left(\alpha a\right)& -\mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha a\right)& \mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}\left(\alpha a\right)& \mathrm{s}\mathrm{i}\mathrm{n}\mathrm{h}\left(\alpha a\right)\\ \mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha a\right)& -\mathrm{c}\mathrm{o}\mathrm{s}\left(\alpha a\right)& \mathrm{s}\mathrm{i}\mathrm{n}\mathrm{h}\left(\alpha a\right)& \mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}\left(\alpha a\right)\end{array}\right].$

Due to the periodicity of the infinite structure in the $x$-direction, the Bloch theorem states that:

14

${\mathbf{\varphi }}_n=e^{iqa}{\mathbf{\varphi }}_{n-1},$

where $q$ is the wave vector in the $x$-direction. The problem can be transformed into an eigenvalue matrix equation, such that:

15

$\left|\mathbf{T}-e^{iqa}\mathbf{I}\right|=0,$

where $\mathbf{T}={\mathbf{K}}^{-1}\mathbf{H}$ and $\mathbf{I}$ is a 4×4 unit matrix.

The dispersion relationship between the wave vector $q$ and frequency $\omega$ can therefore be obtained. For given values of $\omega$, Eq. (15) presents values of $q$. If $q$ has an imaginary part, the corresponding wave is damped in that region and the imaginary part of $q$ can be used to describe the attenuation properties in the band gap.

2.2. Verification

In order to verify the accuracy of the method, the method is used to calculate the band gap of one-stage LR structure that the material of scattering is copper in ref. [28]. In ref. [28], the complex band structure is obtained by using the traditional TM method without considering the mass of rubber, and the model of the unit cell is shown in Fig. 2(a). In this paper, considering the mass of rubber, the unit cell model of the proposed method is shown in Fig. 2(b). The structural parameters and material parameters are the same as those of ref. 28, and the obtained complex band structure is shown in Fig. 3(a). The result of the proposed method (solid line) is shown to range from 302 to 536 Hz. The result of the traditional TM method in ref. [28] (dashed line) is shown to range from 300 to 550 Hz. Fig. 3(b) shows the frequency response function of the one-stage LR structure calculated by the finite element (FE) method. The frequency of band gap ranges from 300 to 535 Hz. Compared with the finite element results in Fig. 3(b), it is found that the results of the two methods are basically the same, but the proposed method is closer to the simulation result. This is mainly because that the mass ratio of the rubber to the scattering is small when the density of the scattering is large, and the mass of rubber has a little influence on the band gap. The proposed method takes into account the mass of rubber, and thereby has better accuracy.

Fig. 2The unit cell model of the different method: a) traditional transfer matrix method, b) the transfer matrix method for considering a distributed spring constant

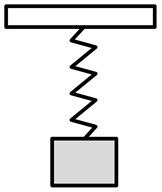
a)

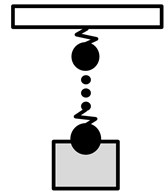
b)

Fig. 3a) The real wave vector of the complex band structure for one-stage LR structure in ref. [28] (solid line; present method, dashed line; TM method), b) the frequency response function as calculated by the FE method for the one-stage LR structure in ref. [28]

a)

b)

2.3. Convergence

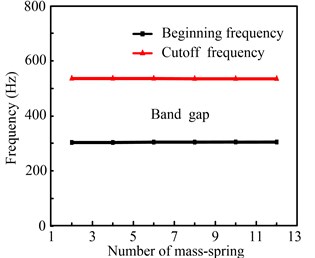
The convergence of the proposed method in the calculation of the band gap in the ref. [28] is shown in Fig. 4. In Fig. 4, When $N$ (the number of mass-springs) is equal to 2, a gap ranging from 302 to 540 Hz is obtained. When $N$ is equal to 4, a gap ranging from 302 to 536 Hz is obtained. With the increase of $N$, the start-stop frequencies of the band gap remain constant and tend to be stable. Therefore, the method has good convergence with less computational requirements.

Fig. 4The convergence of the transfer matrix method for considering a distributed spring constant

3. Application results

The application model of the lightweight multistage LR structure is shown in Fig. 5. In order to analyze the band gap of lightweight multistage structure under the same case of additional mass as the one-stage LR structure, the parameters of the beam is consistent with that in ref. [28]. The multistage local resonators are composed of alternating rubber rings and scattering rings. Each local resonator contains a rubber ring and a scattering ring enclosed the rubber ring. In Fig. 5, the material of the beam is aluminum and the material of the scattering is epoxy. The properties are listed in Table 1. The inner and outer radii of the beam are $r_0=$ 0.007 m and $r_1=$ 0.01 m, respectively. The radii used in the calculation are $r_2=$ 0.015 m, $r_3=$ 0.0195 m, $r_4=$ 0.0245 m and $r_5=$ 0. 0371 m. The lattice constant is $a=$ 0.05 m, and the length of each ring is $l=$ 0.01 m.

Fig. 5The application model of an Euler beam with periodically attached lightweight multistage local resonators

The radial stiffness of the first-stage rubber ring can be calculated using [36]:

where:

Is the shape coefficient. Similarly, the radial stiffness of the second-stage rubber ring is:

where:

Fig. 6 shows the complex band structure of the lightweight multistage LR Euler beam calculated by presented method and traditional method. The results of the presented method that considers the mass of rubber are represented by a solid line in Fig. 6.

Fig. 6The real wave vector of the complex band structure for lightweight multistage LR structure (solid line; present method, dash dot line; the traditional transfer matrix method)

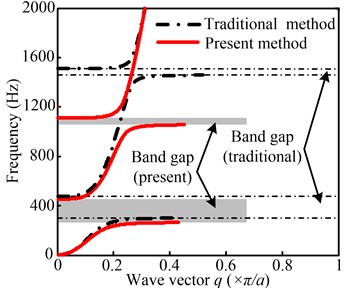
As can be seen from the solid line, the obtained first band gap ranges from 264 to 456 Hz; the obtained frequency range of the second band gap is between 1073 and 1117 Hz; the total width of the two gaps is 236 Hz. The dash dot line in Fig. 6 shows the results of the traditional transfer matrix method. From the dash dot line, the obtained first band gap ranges from 302 to 476 Hz; the obtained frequency range of the second band gap is between 1488 and 1509 Hz. According to the Fig. 6, the results of the proposed method and the traditional method show large differences, especially at the second band gap. This is mainly because that, for the lightweight structure, the role of rubber as mass in locally resonance is more obvious as the frequency increases. Therefore, there is a great difference in the results between the proposed method considered the influence of rubber mass and the traditional method. Compared with Fig. 3(a), we can see that the difference between the proposed method and the traditional method is more obvious with the increase of the ratio of rubber to scattering, and the accuracy of the proposed method is higher.

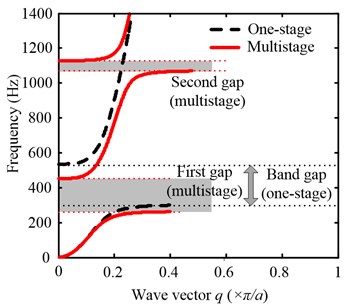
Fig. 7(a) shows the complex band structure of the one-stage structure in reference 28 and the lightweight multistage structure proposed above. The solid line in Fig. 7(a) represents the lightweight multistage structure, the one-stage structure is indicated by the dotted line in Fig. 7(a), and the mass of the local resonators attached to the two structures is the same. Compared with the band gap of the one-stage LR structure in [28], the lightweight multistage LR structure has the second band gap within 0-1200 Hz, and the band gap is more abundant. The beginning frequency of the first band gap is reduced from 302 Hz to 264 Hz, and the total width of the first and second gaps of the lightweight multistage structure is substantially the same as that of the one-stage LR structure. It can be seen from Fig. 7(a) that a lower beginning frequency can be obtained by designing a lightweight multistage LR structure under the same additional mass.

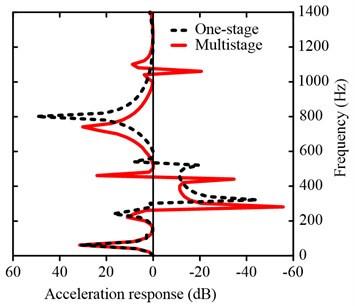
At present the accuracy of the frequency response function calculated by FE method has been proved by experiments in some related papers [26], and the frequency response function is widely used to verify the accuracy of the calculated results [28]. Therefore, the frequency response function of the lightweight multistage LR structure is calculated by the FE method to verify the accuracy of the calculation results. First, eight unit cell models of lightweight multistage LR structures are established. Then, a radial acceleration perpendicular to the axial direction is applied at one end of the structure, which causes the flexural vibration to propagate along the periodic direction of the structure. And pick up the acceleration response at the other end. The obtained band gap ranges from 261 to 452 Hz and from 1046 to 1076 Hz, as shown in Fig. 7(b). Fig. 7 shows that the values of the start-stop frequency of the first gap calculated by the present method and the FE method are fairly well aligned, which verifies the accuracy of the proposed method. But a certain amount of discrepancy does exist between the present method results and the FE results for the start-stop frequency of the second gap. This discrepancy can mainly be ascribed to the discretization of the continuous system in the theoretical study and FE method, which leads to a loss of precision as the frequency increases. The beginning frequency of the low-frequency first gap of a lightweight multistage LR structure is studied below.

Fig. 7a) The real wave vector of the complex band structure for lightweight multistage LR structure (solid line; Multistage, dashed line; one-stage), b) the frequency response function calculated by the FE method

a)

b)

4. A simplified model of beginning frequency of the first gap for a lightweight multistage LR structure

4.1. Simplified model

The beginning frequency of the first band gap in a typical LR PCs is determined by the resonance frequency of the resonator in the same direction. In this resonance mode, the resonators vibrate in specific directions, and the phases of the resonator vibrations in adjacent unit cells are reversed to keep the dynamic balance [32]. The eigenmode shapes of the beginning frequency of first band gap for a lightweight multistage LR Euler beam is shown in Fig. 8. It can be seen from the eigenmode shapes in Fig. 8 that the beginning frequency of the lightweight multistage LR structure should conform to the simplified model in ref. [32] (as shown in Fig. 9(a)). However, the theoretical simplified model of Fig. 9(a) is based on the fact that the density of the scattering is much greater than the density of the rubber. For the lightweight multistage LR structure, the density of the scattering is close to the density of the rubber. In order to further analyze the beginning frequency of the lightweight multistage LR structure, the internal displacement vector of the unit cell A shown in Fig. 8 is shown in Fig. 10. The shaded area shown in Fig. 10 is the rubber. It can be seen that the rubber vibrates mainly with the epoxy scattering. Therefore, the mass of the rubber should be taken into account in the resonators. In this paper, the simplified model of beginning frequency for the lightweight multistage LR structure as shown in Fig. 9(b) is presented.

Fig. 8eigenmode shapes of lightweight multistage LR Euler beam (360 Hz)

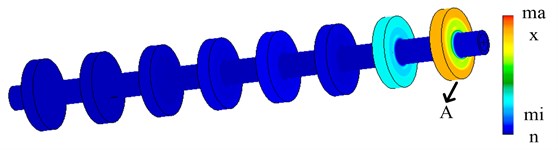
Fig. 9The simplified model for the beginning frequency of the band gaps: a) a simplified model in ref. [32], b) a simplified model of lightweight multistage LR structures

a)

b)

Fig. 10The internal displacement vector of the unit cell A (shown in Fig. 7)

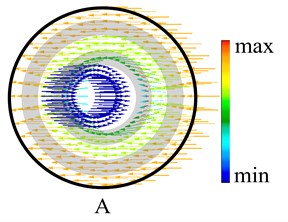
According to the simplified model shown in Fig. 9(b), simplify each rubber into three mass-spring systems ($N_1=N_2=\text{3}$). That is, the simplified model of the beginning frequency is simplified to a series mass-spring systems with $N$ equal to 6. According to the equation of motion of the simplified model, the beginning frequency satisfies the following formula:

17

$\mathrm{d}\mathrm{e}\mathrm{t}\left[\begin{array}{cccccc}{k}_2+k_1-m_1{\omega }^2& -k_2& 0& 0& 0& 0\\ -k_2& k_3+k_2-m_2{\omega }^2& -k_3& 0& 0& 0\\ 0& -k_3& k_4+k_3-m_3{\omega }^2& -k_4& 0& 0\\ 0& 0& -k_4& k_5+k_4-m_4{\omega }^2& -k_5& 0\\ 0& 0& 0& -k_5& k_6+k_5-m_5{\omega }^2& -k_6\\ 0& 0& 0& 0& -k_6& k_6-m_6{\omega }^2\end{array}\right]=0$

where $\omega$ is the circular frequency, $k_i$, $m_i$ are the spring stiffness and mass of the $i$th mass-spring system, respectively.

The beginning frequency of the band gap can be obtained by the Eq. (17).

4.2. Influence of scattering density on model accuracy

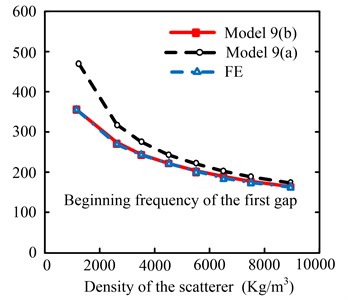
The following choice of structural parameters $r_5$ is equal to 0.029 m, and the rest of the parameters are consistent with the previous text. The beginning frequency of the first band gap of the lightweight multistage LR Euler beam is calculated by the simplified model shown in Fig. 9 (a) (ref. [32]), the simplified model shown in Fig. 9(b) and the FE method, respectively. Fig. 11 shows the variation of the beginning frequency of the first band gap with the scattering density. In Fig. 11, the solid line indicates the simplified model that considers the mass of rubber; the dashed line represents the simplified model that ignores the effect of the mass of rubber; and the dotted line represents the FE method. As shown in Fig. 11, the estimated frequency of the simplified model shown in Fig. 9(b) is consistent with the results of the FE method, which shows that the simplified model has high precision. For the epoxy scattering with smaller density, the simplified model shown in Fig. 9(a) has a large deviation from the FE results. With the increase of scattering density, the deviation decreases gradually. This is mainly because that as the density of the scattering increases, the mass ratio of the rubber to scattering decreases, and the effect of the rubber mass decreases. Thus, the influence of the rubber on the band gap is reduced. Therefore, the proposed simplified model of beginning frequency of the first gap for the lightweight multistage LR structure is reasonable and effective.

Fig. 11Effect of scattering density on the precision of different models for beginning frequency of the first gap

5. Conclusions

In this paper, the transfer matrix method for considering a distributed spring constant is proposed to calculate the flexural band gap of an Euler beam with periodically arranged lightweight multistage local resonators. The proposed method takes into account the mass of the rubber and offers fast convergence with low computational cost. The frequency response function of the multistage LR structure is calculated by the FE method, which verifies the accuracy of the method. Finally, a simplified model of the beginning frequency of the first band gap for the lightweight multistage LR structure is investigated, and the influence of the scattering density on the precision of the simplified model is further analyzed. The research concludes as follows:

1) It is found that the results obtained using the presented method is closer to those acquired by the simulation than the results from the traditional TM method. And the precision of the method is related to the mass ratio of the rubber to the scattering.

2) Under the same additional mass, the light multistage structure has a lower beginning frequency of the first band gap than the one-stage structure. At the same time, there is a richer second band gap in the same range, and the total width of the first and second band gaps is substantially the same as that of the one-stage structure. Therefore, the lower beginning frequency of the first band gap can be obtained by designing a lightweight multistage LR structure compared with the one-stage structure in the same weight, and the lightweight multistage LR structure advances the application of phononic crystal beams in engineering.

3) In addition, the proposed simplified model of beginning frequency for lightweight multistage LR structure introduced the mass of rubber, which gives the rubber the dual physical meaning of mass and spring. As the scattering density decreases, the mass ratio of the rubber to the scattering increases, and the influence of the rubber on the band gap increase. Thus, the precision of the simplified model is becoming more and more obvious. The proposed simplified model contributes to the calculation of the edge frequencies of the band gaps and enhances the understanding of the LR mechanism of PCs.