Abstract
With the rapid development of technology and economy, rough machining has not been able to keep pace with the times. Heavy industry is more and more inclined to the field of precision and ultra-precision machining. During that time, abrasive flow machining technology emerged as the times require. The process of micro cutting is achieved through the contact between abrasive particles and workpiece, so that the accuracy of workpiece's inner surface can be polished, and the accuracy of workpiece improved, which is a representative polishing method. Taking the three-order variable diameter tube as the research object, this paper discusses the polishing characteristics of three level variable diameter pipe with solid liquid two phase abrasive flow. The removal pattern of abrasive flow micro cutting is analyzed, with the collision effect between abrasive particles and wall considered and ignored, which provides technical support for abrasive flow polishing variable diameter pipe parts.
1. Introduction
Abrasive finishing is related to mechanical, material and engineering thermophysics and chemistry. The essence of abrasive flow finishing is the combination of collision and friction effect of two phase fluid on parts [1, 2]. The finishing process belongs to the category of internal turbulent flow. Abrasive flow polishing machine has the characteristics of its accuracy, stability and flexibility, and is not limited by the shape of parts. It can access sections that are complex and difficult to approach. Moreover, it spares complex manual labor, considerably reduces labor intensity and improves parts performance and prolongs service life [3]. There are many factors affecting the abrasive flow performance in solid liquid two phase abrasive flow polishing process, such as abrasive performance, workpiece characteristics, processing parameters [4, 5]. In order to study the effect of abrasive particles collision on the polishing effect of abrasive flow, this paper studies the numerical simulation of abrasive flow polishing for three order variable aperture tubes under the two conditions of taking into account the collisions between the abrasive particles and without considering the collision between the abrasive particles.
2. Polishing parameters selected for solid liquid two phase abrasive flow
2.1. Boundary condition setting
(a) Entrance boundary condition setting. The initial inlet condition is set to the speed inlet and the inlet velocity is perpendicular to the inlet boundary. In order to make the flow state of the calculated flow field turbulent, the initial turbulence intensity is 5 %. Solid phase entry: SiC particles were used as solid phase abrasive particles, and velocity inlet condition was used as well as fluid, with particle concentration of 10 % [6].
(b) Export boundary condition setting. To ensure that the fluid state is turbulent, the outlet is set to unrestrained exit [7].
(c) Wall boundary setting. The essence of abrasive flow polishing process is that the abrasive particles are precisely polished on the wall surface. As for the wall surface of the workpiece, the relative slip produced by the abrasive particles can be seen as the motion of the particle itself [8]. Therefore, in the numerical simulation process, the wall boundary condition is based on the wall boundary condition without slip. The standard wall equation is applied to the near wall area.
2.2. Material parameter setting
The physical properties of liquid and solid particles in solid-liquid two phase abrasive flow numerical simulation should be set up according to physical properties of the material shown in Table 1.
Table 1Basic physical properties of materials
Physical properties | Value | Unit |
Fluid density | 1260 | kg/m3 |
Fluid specific heat capacity | 1800 | j/(kg·K) |
Fluid heat transfer coefficient | 0.15 | w/(m·K) |
Hydrodynamic viscosity | Pa·s | |
SiC abrasive density | 3100 | kg/m3 |
Thermal conductivity of SiC abrasive particles | 120 | w/(m·K) |
SiC viscosity | 5×10-6 | Pa·s |
3. Numerical simulation analysis of abrasive flow polished variable aperture tube
3.1. 3D model establishment and mesh division of variable aperture tube
The inner hole of the three-order variable diameter pipe is staircase changing in axial direction. The three-dimensional model of the three-order variable diameter pipe as shown in Fig. 1 is obtained by SolidWorks software.
Fig. 1Three-dimensional model of three order variable aperture tube

Using the hexahedral grid with better quality, the three-dimensional model of the variable aperture tube was introduced into the grid division software to obtain the grid model as shown in Fig. 2. The quality of grid directly determines whether the result is accurate or not. The better the quality of grid is, the higher the accuracy of computation is. If the grid is too rough, on the other hand, it may cause the computation result not to converge, resulting in large deviation in calculation.
Fig. 2Variable aperture tube mesh model

Then we need to check the quality of grid. Fig. 3 shows the grid quality. The closer the grid quality is to 1, the better the quality of the mesh. From Fig. 3, we can see that the mesh quality of the variable aperture pipe mesh model is larger than 0.5, which indicates that the grid meets the corresponding calculation requirements and can be used for numerical analysis.
Fig. 3Quality detection results of variable aperture tube grid

3.2. Numerical simulation analysis of abrasive flow grinding and polishing of variable aperture tube
The inlet velocity of the particle and the fluid is 30 m/s, the mass flow is set to 0.02 kg/s, the direction of gravity is the same as the direction of velocity, and the rest of the settings are set in Table 1. Taking the end face of the large aperture of the variable aperture tube as the entrance and the end face of the variable aperture tube hole as the exit, the numerical simulation of two kinds of variable aperture tubes under the conditions of particle collision and without considering the particle collision conditions are carried out respectively. The dynamic pressure distribution diagrams of variable aperture tubes under two conditions can be obtained by numerical calculation, as shown in Figs. 4 and 5.
Fig. 4Dynamic pressure cloud diagram of two kinds of variable aperture tubes without considering particle collision conditions

Fig. 5Dynamic pressure cloud diagram of two kinds of variable aperture tubes considering particle collision conditions

The dynamic pressure is the kinetic energy per unit volume of the fluid, which is equal to the difference between the total pressure and the static pressure, which reflects the movement of the fluid in the flow channel. From Fig. 4 and Fig. 5, it can be seen that the variation trend of the flow pressure of the abrasive particles is roughly the same whether the particle collision is considered or not. While considering particle impact, the dynamic pressure of abrasive flow is larger than that without particle collision being taken into account.
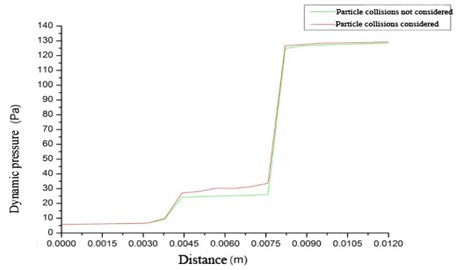
For the three-order variable aperture tube, the dynamic pressure of the first and second order aperture is obviously increased as its aperture gradually decreases, and the dynamic pressure at the second order hole reaches the maximum, which can be mostly attributed to the fact that the fluid moves more vigorously at the smaller hole, which entails the dynamic pressure augment. As the fluid flows from the large diameter tube to the small diameter tube, the dynamic pressure is increasing and reaches the maximum value at the third order of the smallest pore tube. It is worth noting that when applying the abrasive flow polishing technology to variable aperture tube finishing, the processing effect of the tapered tube is better than that of the diffused tube and the processing effect at small aperture is better than that of large aperture. In order to reflect the change law of dynamic pressure more intuitively, the axis of the cross section is selected as the datum line, and the dynamic pressure values along the line are made into a change trend line diagram, as shown in Fig. 6.
It can be clearly seen from Fig. 6 that the dynamic pressure values of the variable aperture pipes under two different conditions are approximately the same. At the initial stage, the two lines almost coincide, which means that the collision between particles at the first order is smaller, and the effect on the fluid is smaller. After the pore size changes, the particle impact at the pore size change is more intense, and the influence on the fluid is greater. Therefore, the dynamic pressure value with the condition of particle collision considered is greater than that of the particle impact condition ignored. From the dynamic pressure variation analysis of the variable aperture tube, it can be seen that the particle collision has a certain effect on the movement of the fluid during the polishing process of the abrasive flow, and the effect is more favorable to the processing effect, and it can significantly advance the polishing result of the abrasive flow. In order to better study the movement of particles, we analyzed particle distribution cloud pattern during abrasive flow polishing process.
Fig. 6Change trend of dynamic pressure value of variable aperture tube
Figs. 7 and 8 are two particle size distributions of two variable aperture tubes under different conditions. When particle collision is not considered, the distribution of particles in the first and second order is not obvious and the particle flux in the near wall region is higher than that in the middle area. This means that the movement of the particles on the wall is more intense compared to the middle area, and the particle flow begins to increase at the second and third order changes, for the change of the pore size leads to the pressure change, which makes the particle velocity increase and rises the particle flux. Without considering particle collision, the motion of particles is almost the same as that of fluid, and their motion trend is smaller; Under the consideration of particle collision, the distribution of particles at variable pore size has obvious changes. In the place where the size of each large aperture changes to the small aperture, the distribution of the particles undergo a similar change. The particles have a certain accumulation at the variable diameter. With the change of the aperture and the increase of the pressure, the particle has a greater mass flow flux in the small aperture.
Fig. 7Particle size distribution of two kinds of variable diameter pipes without considering particle impact conditions

Fig. 8Particle size distribution of two kinds of variable diameter pipes considering particle impact conditions

4. Conclusions
1) In the process of solid liquid abrasive flow polishing, liquid phase fluid drives solid particles to move in the channel formed on the workpiece surface. Therefore, the movement of fluid and abrasive has an immediate effect on the abrasive flow polishing effect. The abrasive grains slide along with the fluid, micro cutting of the surface material to be processed, so as to achieve the removal effect of the workpiece surface material to be processed and accomplish the polishing of the abrasive flow on the workpiece surface.
2) Due to the accumulation of particles at small holes in the three-order variable aperture tube, the collision between particles will be aggravated, the motion of particles at small aperture is far more intense, so is the irregular motion of particles in the near wall area.
References
-
Li Junye, Qiao Zemin, Yang Zhaojun, et al. Influence of abrasive concentration on the processing quality of abrasive flow in mesoscopic scale. Journal of Jilin University, Vol. 47, Issue 3, 2017, p. 837-843.
-
Li Chen, Ji Shiming, Tan Dapeng, et al. Study of near wall area micro-cutting mechanism and finishing characteristics for softness abrasive flow finishing. Journal of Mechanical Engineering, Vol. 50, Issue 9, 2014, p. 161-168.
-
Kenda Jani, Pušavec Franci, Kopac Janez Modeling and energy efficiency of abrasive flow machining on tooling industry case study. Procedia CIRP, Vol. 13, 2014, p. 13-18.
-
Sun Shufeng, Ji Shiming, Tan Dapeng Research on turbulence regulation of low viscosity liquid-solid two-phase abrasive flow and finishing technology of structural surfaces. China Mechanical Engineering, Vol. 22, Issue 19, 2011, p. 2349-2353.
-
Li Junye, Wei Lili, Zhang Ximing, et al. Quality analysis of T-tube with solid-liquid two-phase abrasive flow polished. Journal of Measurements in Engineering, Vol. 5, Issue 2, 2017, p. 77-86.
-
Li Junye, Hu Jinglei, Dong Kun, et al. Technological parameter optimization and quality effects on solid-liquid phase abrasive flow polishing. Optics and Precision Engineering, Vol. 25, Issue 6, 2017, p. 1534-1546.
-
Spratling M. Nanofinishing of freeform surfaces using abrasive flow finishing process. Proceedings of the Institution of Mechanical Engineers Part B Journal of Engineering Manufacture, Vol. 6, Issue 9, 2015, p. 206-207.
-
Li Junye, Zang Xiang, Meng Wenqing, et al. Numerical simulation for machining S-tube by abrasive flow with various particle volume fractions. Vibroengineering Procedia, Vol. 16, 2017, p. 134-137.
About this article
The authors would like to thank the National Natural Science Foundation of China No. NSFC 51206011, Jilin Province Science and Technology Development Program of Jilin Province No. 20160101270JC and No. 20170204064GX.
