Research on performance prediction and optimization of road header based on regression model

2.1. The establishment of regression function

The regression model is essentially an approximate function, which uses a limited number of known parameters to fit an unknown functional relationship [7]. At present, there are many types of function expressions used in the regression model. Among them, the polynomial-based regression function can express a complex response relationship with simple parameters and has good robustness [8].

Before establishing the regression model, it is necessary to first establish the target variables and design variables. For the performance prediction model of the road header, it is assumed that the same rock layer satisfies the isotropy, so the rock hardness is not considered as a function variable. The drilling speed ($y$, m/h) is used as the target variable, and the cutter head torque ($x_1$, kN·mm), jack thrust ($x_2$, kt), cutter head rotation speed ($x_3$, r/min), screw speed ($x_4$, r/min) and other four controllable driving parameters are used as design variables. As shown in Table 1, all discrete parameters are obtained through on-site engineering tests.

The least squares method is used to fit the intrinsic relationship between the target variable $Y\left(y\right)$ and the design variables $X$($x_1$, $x_2$, $x_3$, $x_4$). The function expression is:

where $\widehat{Y}\left(X\right)$ is a regression function that needs fitting; $\epsilon$ is a fitting error, $\epsilon -N\left(0,{\sigma }^2\right)$.

In order to improve the accuracy of the regression function, the interaction relationship between every two design variables is considered in the paper. The quadratic response expression is used to represent the regression function. Its expression is:

where $b_0$, $b_i$, $b_{ij}$ are all undetermined coefficients.

Convert Eq. (2) to matrix form as followed:

In the formula, $\mathbf{D}$ is the design matrix, which represents the sample vector of the regression model. $\mathbf{B}$ is the regression coefficient vector.

The key to solving the regression function is the determination of each polynomial coefficient $b_0$, $b_i$, $b_{ij}$. In general, the least squares method can be used to process the error, first convert it to the parameter s, and its calculation expression is:

where $y_i$ is the actual discrete response; $n$ is the number of sample measurements.

It can be concluded that the solution of each element in the regression coefficient vector $\mathbf{B}$ is:

Substituting the data in Table 1 into each formula, the regression function can be finally fit as:

2.2. Error analysis

Since the regression model is an approximate function, there must be an error $\epsilon$ between the actual target variable and if the error value is very small or within the allowable range. It can be indicated that the fitted regression model has good feasibility. In general, there are three kinds of parameters used for polynomial regression function error checking, such as fitting determination coefficient $R_d$, correction determination coefficient $R_a$, and root mean square error $R_m$.

The calculation formula for fitting the coefficient of determination is:

where $S_T$ is the total square sum of the model; $S_R$ is the regression sum of squares; $S_E$ is the sum of squared residuals.

The total sum of squares $S_T$ is calculated as:

where $y_i$ is the actual measured value of the target variable, ${\stackrel{-}{y}}_i$ is the average value, $n$ is the number of sample measurements.

The calculation expressions of regression squared $S_R$ and residual squared sum $S_E$ are:

where ${\widehat{y}}_i$ is the target variable obtained by the regression function.

Calculation formula of correction coefficient $R_a$ is:

where $p$ is the number of polynomials in the regression function.

The root mean square error $R_m$ has an expression is:

Substituting the data in Table 1 into the error judgment formula, the final fitting accuracy of the regression model is shown in Table 2. As can be seen in Table 2, the regression model has a low fitting error. To further meet engineering needs, the root mean square root error $R_m$ can be verified by increasing the number of samples.

3.1. Sample data mining method

A good predictive model can achieve good accuracy even without adjusting parameters, which requires a high stability of the objective function. In order to further verify the reliability of the regression model for performance prediction, the root mean squared error of the model error is calculated using different sample data mining methods (including on-site measurement samples). At present, there are many methods for sampling data points, such as full factor method, partial factor method, orthogonal design method, center combination method, and Latin method. In this paper, orthogonal design method, center combination method and Latin square design method are used to obtain discrete design variables and target variables respectively. These three methods all use Tab.1 to determine the effective range of data mining points, and increase the total number of samples by increasing the number of horizontal factor.

3.2. Error analysis with different sample sizes

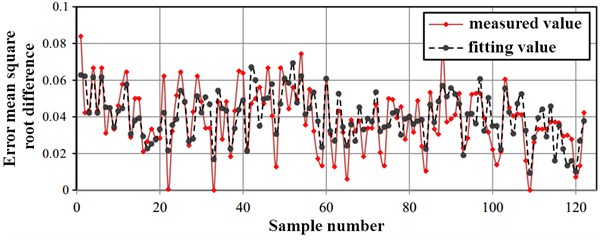
The RMS comparison results between the samples of different data points and the measured values are shown in Fig. 1, Fig. 2, and Fig. 3, respectively. It can be seen in these figures that the root mean square error of the sampling method for different sample data is similar [9]. Compared with the orthogonal design method and the Latin square design method, the tunneling performance predicted by the center combination method is used to predict the regression function and the actual target variable. The error between the two is smaller; the regression function fitted in the paper has higher precision and good feasibility, and can be directly used to optimize the mathematical model [10].

Fig. 1Comparison of central composite fitting method and measured method

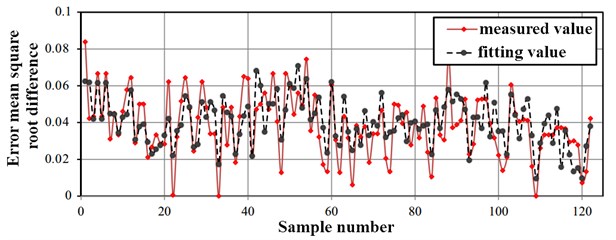
Fig. 2Comparison of orthogonal design fitting method and measurement method

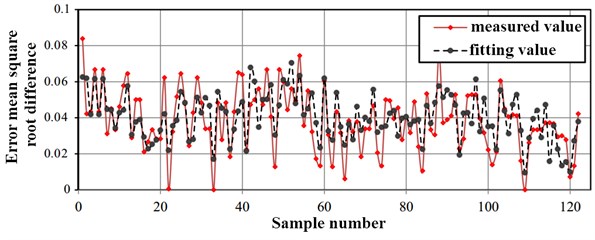
Fig. 3Comparison of Latin square design fitting method and measurement method

4.1. The construction of the optimized mathematical model

According to engineering practice, it is known that the excavation work has significant complex nonlinear characteristics. Under a certain excavation parameter, it is difficult to achieve the best production efficiency, that is, to ensure that the drilling speed is at a maximum value. Through the regression model fitted in this paper, combined with advanced optimization algorithms, the maximum target variable within the design variable can be searched efficiently. The calculation result is not limited to the current rock layer structure. In essence, the optimization of the excavation performance is to achieve the optimization of the excavation parameters through mathematical calculations and to obtain the maximum drilling speed parameters. The prediction of the performance of the road header is a key issue in realizing the full-face tunneling engineering of coal mines. From the regression model, the objective function is not a simple linear function. The entire prediction calculation depends on multiple variables and has high reliability.

The optimization mathematical model is the basis for searching for extremely target variables, including objective functions and constraints, where the objective function is constructed based on a regression function, as shown in Eq. (12). According to the working conditions of the road header, it can be seen that under normal conditions, the cutter head torque range is 1500-3000 kN·m, the jack thrust range is 800-1500 t, and the rotary speed range of the cutter head is 1-3 r/min. The speed range is 5-15 r/min:

where ${\underset{\_}{x}}_i$, ${\stackrel{-}{x}}_i$ are the minimum and maximum values of the four design variables, respectively.

4.2. Application of extremum search algorithm

According to the characteristics of the optimized mathematical model constructed, it can be known that the optimization problem of excavation performance is a typical quadratic nonlinear optimization problem, and it has multiple independent variables, and there are interactions among the independent variables. Therefore, the optimization value of the mathematical model is not a single solution. For the processing of this type of mathematical model, there are more algorithms applied in engineering: genetic algorithm, simulated annealing algorithm, particle swarm optimization algorithm, and quadratic programming algorithm and so on.

Taking into account the characteristics of each algorithm, the quadratic programming algorithm is used to achieve the search of the target. The quadratic programming algorithm can perform direct search when dealing with quadratic polynomial functions, but the convergence speed is difficult to control. If the accuracy judgment is unreasonable, it is difficult to meet the termination criterion, so the self-adjustment convergence speed needs to be continuously adjusted according to the constraints of the regression function.

Target extreme value search is a typical iterative algorithm. In order to improve the stability of the calculation process and achieve global convergence, the total number of samples can be defined first, and then the linear search factor can be combined with the Lagrange value function to obtain reasonable results. The iteration step. In the self-adjustment of the convergence speed, it is necessary to change the iteration step according to the accuracy judgment criterion. In general, the iterative step size ${\alpha }^K$ can be used to characterize the difference between before and after each iteration:

where $X^{K+1}$ is the design variable after iteration, $X^K$ is the design variable calculated by the current $K$th search, and $S^K$ is the iteration length of the current $K$th search calculation.

In the calculation of the secondary sequence plan, two basic operation steps need to be completed: the determination of the search direction and the update of the iteration step size. The two steps are in an alternating state until the accuracy reaches the determination target.

4.3. Analysis of optimization results

In this paper, MATLAB performs an extremum search under the condition that the total number of samples is 20 to 120 (obtained from the central composite design method), and finally the optimal solution set is shown in Fig. 5. As can be seen in Fig. 4, the larger the number of samples, the more solution sets that satisfy the constraints, and the maximum value of the optimization goal is 1.12. According to the convergence criteria and accuracy criteria, the optimal configuration of each design variable at this time can be concluded as shown in Table 3.

Fig. 4The optimal solution set for different sample sizes

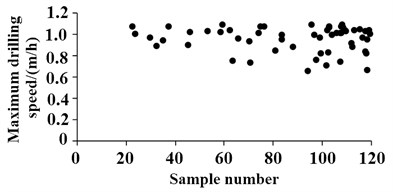
In order to ensure the safety under the excavation conditions, the optimized objectives and design variables obtained are to be constructed on site. According to the observation of the surface subsidence amplitudes, it was found that the settlement value of more than 90 % of the observation points was less than 1.5 mm during the entire excavation process, which fully satisfied the coal mine production requirements.