The shear characteristic and failure mechanism study of infilled rock joints with constant normal load

2.1. Specimen preparation

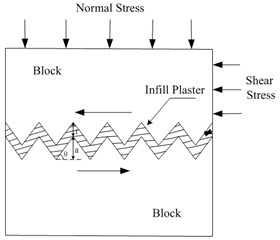
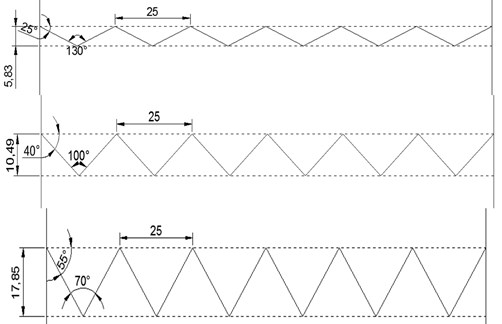
In the test, the blocks were a mixture of 42.5 Portland cement, fine sands which particle size less than 2 mm and water with a weight ratio of 2:2:1. The specimen size is 150 mm×150 mm×150 mm, the width of a single sawtooth is 25 mm, the number of the sawtooth is 6, which means the height varies with the asperity angle. The asperity angles $\theta$ of the structure surface was 25°, 40° and 55°, as shown in Fig. 1. The plaster is used for 1:2 filling, that is $t$/$a$ was 0.5. In order to improve the accuracy of the test results, the specimens were layered in the pouring process and tamped in a timely manner. At the same time, the specimens were kept in the curing box for 28 days after standing in the mold for 24 hours to increase the stability of the specimens. The basic mechanical parameters of the plaster are shown in Table 1.

Fig. 1Experimental models: a) the specimen containing infilled plaster, b) θ= 25°, 40° and 55° with no infilled plaster

a)

b)

2.2. Penetration tests

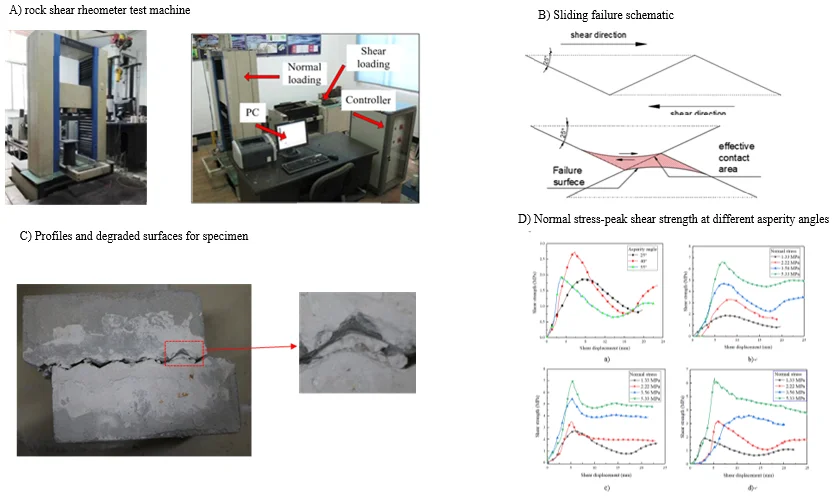
RYL-600 rock shear rheometer testing machine, which is composed of normal and shear loading systems, control system and PC system, is shown in Fig. 2. The maximum vertical and horizontal loads of the machine were 600 KN and 300 KN. To diminish friction effects, the top and lateral surfaces of the block were lubricated before testing. In the test, the shear mechanical characteristics of regular sawtooth surfaces with different asperity angles of 25°, 40° and 55° under different normal stresses were evaluated. Since the specimen is easily fractured under high normal pressure, the test was conducted at normal pressures of 30 KN (1.33 MP), 50 KN (2.22 MP), 80 KN (3.56 MP) 120 KN (5.33 MP). The normal loading rate was 100 N/S and the test plan is shown in Table 2. Shear begins after the normal load has stabilized for 30 minutes. A constant shear rate of 2 mm/min and a shear displacement of 20 mm were applied. At the same time, the normal and shear displacements, the normal and shear stresses ware recorded every few seconds. The shear test was stopped when the residual strength was stable.

Fig. 2RYL-600 rock shear rheometer test machine: a) normal loading, b) parts of the test machine

a)

b)

3.1. Failure modes

The results of the comprehensive shear stress-strain curves and the test results show that the types of specimen failure are mainly affected by the asperity angle. This is because of the fact that the asperity angle normally has an effect on the effective contact area between the upper and bottom parts of the specimen, resulting in an increase in the peak shear strength. When the upper part of the specimen climbs before the specimen destroyed, the contact area between the upper and bottom parts means the effective contact area, as shown in Figs. 3(b), 4(b) and 5(b). With the increasing asperity angle, the failure mode changes and the effective contact area is increasing as well. In addition, the height of sawtooth has an effect on the effective contact area obviously.

3.1.1. Sliding failure

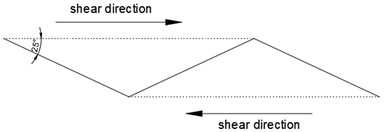
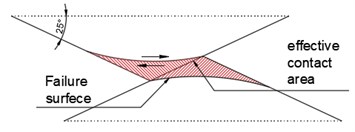
When the asperity angle is 25° and the normal stress is 1.33 MPa or 2.22 MPa, the shear displacement curve basically displays a sliding failure curve. The specimen slips along the joint surface and the sawtooth tip wears while it is not sheared. The asperity angle does not change, and the joint surface undergoes the dilatancy effect is more obvious than other asperity angles. In the area close to the joint surface, the block is squeezed which is mainly caused by shear damage. The sawtooth before shearing is shown in Fig. 3(a), it shows that the failure surface mostly performs arc shape after direct shear test and the sliding failure schematic is shown in Fig. 3(b). On the other hand, the specimen A-1 is mainly caused by the sliding failure, as shown in Fig. 3(c). The sawtooth portion of the specimen structural surface was ground, and the surface was worn, but there is not any damage basically. It should be noted that the climbing effect is obvious during the practical destruction.

Fig. 3a) The sawtooth of A-1, b) sliding failure schematic, c) profiles and degraded surfaces for specimen A-1

a)

b)

c)

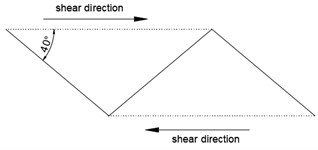
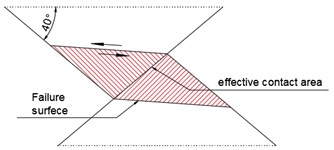
Fig. 4a) The sawtooth of A-2, b) Shear failure schematic, c) profiles and degraded surfaces for specimen A-2

a)

b)

c)

3.1.3. Tensile failure

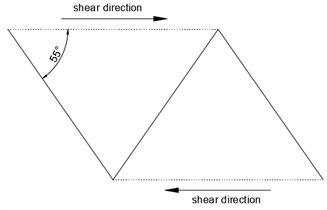
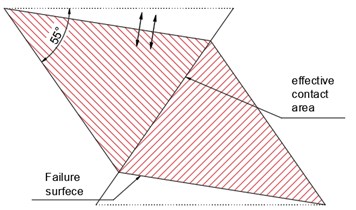
When the asperity angle of the specimen is large such as 55° or the normal stress is 5.33 MPa, the main damage occurred is a tensile failure. The sawtooth portion of the specimen is directly sheared from the location of the bottom, and there are obvious traces of cracks and sawtooth damage. At the same time, the cutting effect is more obvious during the practical damage process. When the normal stress and the asperity angle are large, the effective contact area of the sawtooth increased, resulting in increasing friction between the upper and bottom block. Also, the force between the sawtooth form a bending moment. The bending moment and friction induce the formation of the final pull to crack afterwards. Compared with shear failure, the destruction of tensile failure is more severe. As shown in Fig. 5, the infilled joints are squeezed closely with the increasing damage area. For the specimen B-3, the tensile failure mainly occurs.

Fig. 5a) The sawtooth of B-3, b) tensile failure schematic, c) profiles and degraded surfaces for specimen B-3

a)

b)

c)

3.2. Analysis of strength characteristics

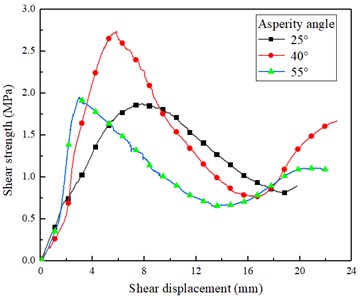
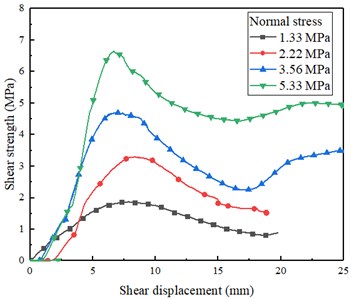
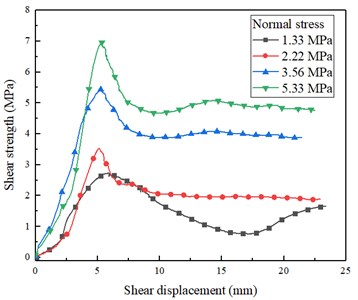
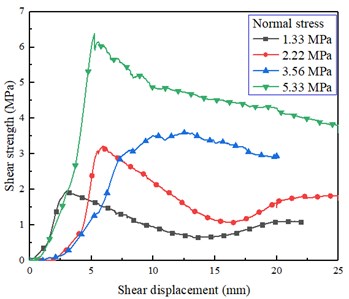
Fig. 6(a) depicts different shear stress-displacement curves of asperity angles under the normal stress of 1.33 MPa. During the early stage of shear displacement, the shear strength increases rapidly, basically showing a linear relationship. And the slope increased by the increasing asperity angles. When the peak shear strength was reached, the shear stresses begin to decrease as the shear displacement increases. After the participation curve undulating wavy and the second peak is lower than the first one. When the asperity angle is 25°, 40° and 55°, the peak shear displacement are 7.65 mm, 5.81 mm and 2.99 mm, respectively. It can be seen that under the same normal stress, the larger the asperity angle is, the smaller the peak shear displacement is. Fig. 6(a) depicts different shear stress-displacement curves of normal stresses under the asperity angle of 40°.

In the early stage of micro fracture compaction, the faster the shear stress rises, the greater the normal stress is. The entire residual curves do not show significant fluctuations. However, the residual strength of the specimen with 1.33 MPa is relatively small, while the specimens with 2.22 MPa, 3.56 MPa and 5.33 MPa display obvious residual strengths. Under the same normal stress, the residual strength is proportional to the normal stress. The peak shear displacements of 2.22 MPa, 3.56 MPa and 5.33 MPa curves also increase with the increase of normal stress. As shown in Fig. 6(b) and 6(c), the trend of shear stress-displacement curves is almost the same. But in Fig. 6(d), the shear stress-displacement carves are a little different which due to the tensile failure mode.

Fig. 6Typical shear stress-displacement curves: a) asperity angles under the normal stress of 1.33 MPa, b) asperity angle of 25° under different normal stresses, c) asperity angle of 40° under different normal stresses, d) asperity angle of 55° under different normal stresses

a)

b)

c)

d)

3.3. Analysis of asperity angle on peak shear stress

Fig. 7 depicted that the peak shear strength of the same asperity angle increases with the increase of normal stress. There is a linear relationship between the peak shear strength and normal stress. However, under the same normal stress, the peak shear strength was not increased with the increase of asperity angle. The peak shear strength at the asperity angle of 40° is the greatest, while the difference between 25° and 50° is not obvious. The overall trend is that the curve increases first and then decrease. And the effective contact area becomes greater with the increasing asperity angles. Since the force causing sawtooth damage under tensile failure is less than the force under shear failure, the peak shear strength of 55° is smaller than that of 40°. Besides, the peak shear strength of 25° is smaller than that of 40° resulted from the failure mode changes from sliding to shear. In addition, the shear force at failure is increasing by increasing angle.

The obvious tensile cracks can be seen in Fig. 8(c). At the same time, the asperity angle of 55° shear effect is more intense, pulling a wider range of cracks. This is because the infilled plaster is relatively soft and squeezed to produce a stress component perpendicular to the sawtooth surface. It induces a large tensile stress at the bottom of the sawtooth. Thin specimen coupled with weak tensile strength can result in the tension damage as well. The surface and side of the specimen with the asperity angle of 25° are almost nondestructive, and the failure mode is sliding failure. The failure surface of the specimen with the asperity angle of 40° mostly occurred in the middle of sawtooth, and the failure mode is a shear failure.

Fig. 7Normal stress-peak shear strength at different asperity angles

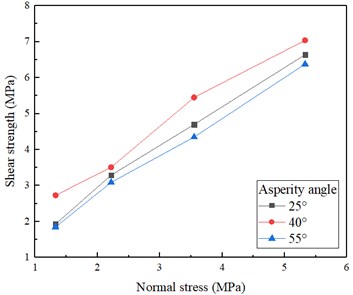
Fig. 8View of specimens: a) A-1, b) C-2, c) B-3

a)

b)

c)

3.4. Analysis of the dilatancy characteristics

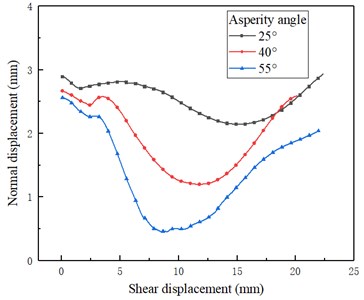
The normal displacement of the specimen changes mainly because the upper part of the specimen sliding along the sawtooth surface and the infilled plaster is squeezed. Under the same normal stress, the specimens with three different asperity angles have a steady decrease with the increase of shear displacement before reaching the peak shear strength. When the peak shear strength is reached, the normal displacement increases abruptly, and the curve shows a small area of the bulge, due to the sudden compression of the specimen. After that, the normal displacement continues to decrease, reaching the minimum when reaching the residual strength. Finally, the normal displacement continues to increase until it is approximately equal to the initial normal displacement, as shown in Fig. 9(a). This stage is mainly because sawtooth was cut after the grinding, the sawtooth of the upper part enter into the next recess of the bottom part, along with the sawtooth surface sliding caused by the increase normal displacement. It can be concluded that the larger the asperity angle is, the larger the normal displacement of dilatancy angle and dilatancy are. The dilatancy curve of the same asperity angle specimen will also be affected by the normal stress. Under the same asperity angle, when the displacement about 5 mm, the specimen reached the peak shear strength. After that, the normal displacement of the specimen increased with the increase of the normal stress.

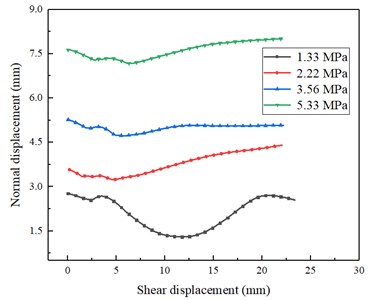
With the same asperity angle of 40°, the dilatancy curves show similar trends with different normal pressures, as shown in Fig. 9(b). However, greater normal stress results in greater normal displacement. This is because the infilled plaster locates between the upper part and the bottom part of the specimen. When the normal stress is increased, the greater pressure acts on the plaster and the plaster is squeezed more severely, which causes greater normal displacement. Therefore, the infilled plaster contributes more to normal displacement.

Fig. 9Typic dilatancy curves: a) asperity angles under the normal stress of 1.33 MPa, b) asperity angle of 40° under different normal stresses

a)

b)

3.5. Verification between the analytical model and test results

In order to forecast the shear strength changed by asperity angles and normal stresses, T. T. Papaliangas et al. [19, 20] and Ladanyi and Archambault [31] proposed analytical models, which is based on the infilled rock joints tests. Shear strength falls between $T_{max}$ and $T_{min}$. $T_{max}$ is the maximum shear strength of infilled joints, $T_{min}$ is the potential minimum shear strength with filling thickness. The thickness, filling material, asperity angles, and normal stress would influence the value of $T_{max}$ and $T_{min}$. It is reasonable to assume $T_{min}$ equal to the shear strength of the fill for rough and undulating joints. However, for planar and undulating joints, the strength along the block and filling interface is considered to be the value of $T_{min}$. $T_{min}$ usually smaller than the shear strength of the filling plaster. In terms of percentages of stress ratios, it was proposed for the prediction of the shear strength of infilled joints, as follows:

where $\mu =\left(\frac{T}{{\sigma }_n}\right)\times 100$, ${\mu }_{min}=\left(\frac{T_{min}}{{\sigma }_n}\right)\times 100$, and $n$ is a function of the filling thickness:

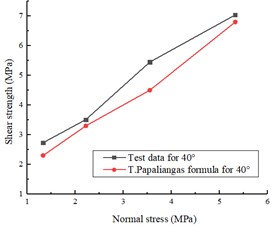
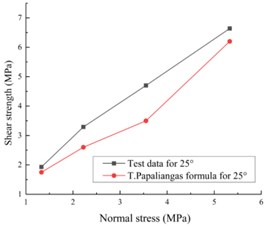
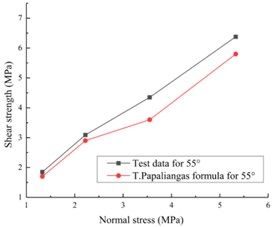
where $0<t/a<c$, $t$ is the thickness of filling material, and a is the average roughness of discontinuity. As shown in Table 1, $c$ and $m$ are constants gained by experiments, but $c=$ 1.5 and $m=$1 determined by a series of experiments for peak shear strength. Combined with Barton formula shows, $T_{min}=C_0+{\sigma }_n\mathrm{t}\mathrm{a}\mathrm{n}{\phi }_0$, which $C_0$ and ${\phi }_0$ are the Cohesion and Friction angle of the infilled plaster. In the formula above, $T_{min}$ is only affected by the normal stress while $T_{max}$ is affected by many factors. All specimen prepared for this test have the ratio $t$/$a=$ 0.5, and the n value can be obtained by numerical model and it equals to 2/3. Based on the comparison, the laboratory test results are in good agreement with the analytical model, as illustrated in Fig. 10.

The results of the experiment are mainly consistent with the trend of the analytical results, and the comparison curve of 55° is highly consistent among the three asperity angles. However, the analytical results are smaller than the test results, which is because the value of c and m in the Papaliangas formula in this experimental model is small. Besides, the mechanical parameters of plaster are different from plaster used in the analytical model. At low asperity angles, the infilled plaster is squeezed into a half horizontal plane during shear. At high asperity angle, the effect of roughness on the peak shear strength will be enhanced and the impact of the infilled plaster on the shear strength will be reduced.

Fig. 10The test results are compared with T. T. Papaliangas formula with different asperity angles: a) the asperity of 25°, b) the asperity of 40°, c) the asperity of 55°

a)

b)

c)