Semi analytical solution of a rigid pavement under a moving load on a Kerr foundation model

Alisjahbana, Sofia W.; Alisjahabana, Irene; Kiryu, Shota; Gan, Buntara S.

doi:10.21595/jve.2018.20082

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 August 2018

Check for updates

Semi analytical solution of a rigid pavement under a moving load on a Kerr foundation model

Sofia W. Alisjahbana¹

Irene Alisjahabana²

Shota Kiryu³

Buntara S. Gan⁴

¹Faculty of Engineering and Informatics, Bakrie University, Jakarta, Indonesia

²Department of Civil and Environmental Engineering, Stanford University, Stanford, USA

³Department of Architecture, Graduate School of Engineering, Nihon University, Koriyama, Japan

⁴Department of Architecture, College of Engineering, Nihon University, Koriyama, Japan

Corresponding Author:

Buntara S. Gan

Cite the article Download PDF

Downloads 1874

WoS Core Citations 7

CrossRef Citations 4

Abstract

This paper analyzes the dynamic response of assumedly rigid road pavement under a constant velocity of traffic loads moving on its surface. The model of the rigid road pavement is a damped rectangular orthotropic plate which is supported by an elastic Kerr foundation. Semi-analytical solutions of the dynamic deflection of an orthotropic plate, with semi rigid boundary conditions are presented by using governing differential equations. The natural frequencies and mode shapes of the system are then, solved by using the modified Bolotin method considering two transcendental equations as the results of solving the solution of two auxiliaries Levy’s plate type problems. The moving traffic loads modeled by varying the amplitudes of dynamic transverse concentrated loads harmonically. Numerical studies on the soil types, foundation stiffness models, varying constant velocities and loading frequencies are conducted to show the effects of the dynamic response behaviors of the plates. The results show that the dynamic responses of the rigid road pavement influenced significantly by the type foundation stiffness models and velocity of the moving load.

1. Introduction

The vibration response of rectangular orthotropic plates is an interesting subject because of its widespread applications in structural engineering and transportation engineering. In bridge analysis, different models have been studied and investigated by researchers for rigid highway and airport pavements. In most of the previous works the type of plates considered are isotropic rectangular plates which are uniform in all directions. In reality, not all plates are isotropic. Another important type of plate is the orthotropic rectangular plate, which has been used to model the dynamic response of rigid concrete pavements. According to Alisjahbana and Wangsadinata, the dynamic moving traffic load can be represented by a single concentrated harmonic loading, moving with a constant speed along the mid-side of the plate [1]. It was found that a dynamic load approach will lead to a better economical solution in comparison to solutions obtained using the conventional static load approach.

Conventional methods of rigid pavement design are using the elastic Winkler foundation model which is obtained from the static analytical solutions of infinite plates rest on elastic soil assumption. These were investigated by Westergaard in 1926 [2]. In this elastic Winkler foundation model, the interconnections among the soil layers are neglected, leading to limitations in the physical model of the sub-soil system [3]. These limitations can be eliminated by modeling the sub-grade soil medium by using two-parameter model, providing a shear interaction between independent spring elements.

Several researchers have verified the applicability of soil medium representation by using two parameter models in static [4, 5], post buckling [6, 7] as well as dynamic models [1, 8-10]. Gan and Nguyen presented the two parameter model of soil medium in the large deflection analysis of functionally graded beam [11].

Paliwal and Ghosh studied the stability of rectangular orthotropic plates on a Kerr soil foundation model subjected to the in-plane static stresses in the orthogonal directions [12]. The dynamic lateral loads are not discussed in their work. The Kerr model is one of the most advantageous models. However, due to the existence of an upper spring layer, no concentrated reactions occur. Kneifati has shown that more accurate base response of the flexible plates and beams subjected to a uniform load and boundary forces was obtained by using the Kerr model compared to the Pasternak and Winkler models [13]. In addition, the Kerr model moreover shows comparable results with the continuum elastic theory. Therefore, in this paper, the authors will analyze the dynamic behavior of the rigid road pavement rests on a Kerr model and subjected to a moving load.

In most researches done previously, rigid road pavements are modeled as an orthotropic plate. Furthermore, it is commonly resting on an elastic foundation model such as the Pasternak or Winkler models. However, according to Paliwal and Ghosh in 1994, the Winkler model is unable to represent the behavior of soil medium materials with a larger void ratio or stiffer clay. Additionally, the Pasternak model is only better in predicting the behavior of hard soils. On the other hand, Kerr foundation model has more advantageous models due to no concentrated reactions occur due to an addition of an upper spring layer [12].

In this study, the dynamic response of a rigid road pavement modeled as a thin orthotropic plate rests on the Kerr model is investigated. To take into account the existence of the tie bars and dowels along its edges, the boundary conditions along its edges are semi rigid condition allowing the rotation at the supports and the translational movement at the edges. These type of boundary conditions are solved by using the Modified Bolotin Method [1]. There has been no previous research using this specific method to study the dynamic response of the rigid road pavement subjected to a moving load. In this paper, semi analytical solution is used to calculate the dynamic deflection and internal forces distribution of the plate subjected to loading with constant velocity. The applicability of the present method is highlighted by solving the maximum dynamic deflection of the system for different types of soil conditions and elastics foundation model in order to design better rigid road pavements.

2. Governing equation

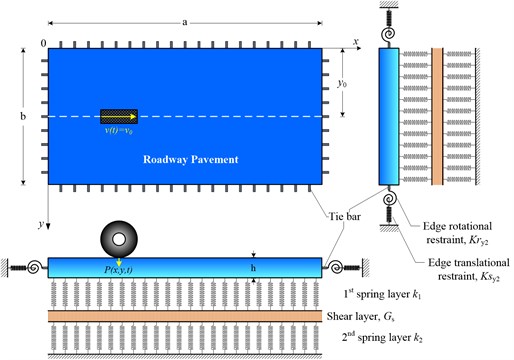
In this paper, a rigid pavement resting on Kerr foundation is considered. The orthotropic plate is semi rigid along its edges. It is considered to be of uniform thickness $h$ . The dynamic transverse load acting on the orthotropic plate is $q (x, y)$ . Based on the work of Paliwal and Ghosh [12], the governing differential equation of the rigid pavement subjected to the lateral load is given by:

1

D_{x} \frac{\partial^{4} w}{\partial x^{4}} + 2 b \frac{\partial^{4} w}{\partial x^{2} \partial y^{4}} + D_{y} \frac{\partial^{4} w}{\partial y^{4}} = q - p_{1},

where $D_{x}$ , $D_{y}$ are the flexural rigidities of the plate in the $x$ direction and the $y$ direction respectively, $B$ is the torsional rigidity of a plate and $p_{1}$ is foundation response. Because the Kerr model [14] consists of two axial springs ( $k_{1}$ and $k_{2}$ ) and shear spring layer ( $G_{s}$ ), the deflection of the plate can be given as [13]:

2

w (x, y) = w_{1} (x, y) + w_{2} (x, y) .

The contact pressures under the orthotropic plate and the shearing layer are given by $p_{1}$ and $p_{2}$ , respectively, where:

3

p_{1} (x, y) = k_{1} w_{1} = k_{1} (w - w_{2}),

4

p_{2} (x, y)

k_{2} w .

The shearing layer was governed by the following differential equation:

5

k_{2} w_{2} - G_{s} \nabla^{2} w_{2} = p_{1} .

Eliminating $w_{2}$ from Eq. (3) and (5), we obtain:

6

(1 + \frac{k_{2}}{k_{1}}) p_{1} - \frac{G_{s}}{k_{1}} \nabla^{2} p_{1} = k_{2} w - G_{s} \nabla^{2} w .

By substituting $p_{1}$ of Eq. (3) into Eq. (6) and by taking into account the moving load, the structural damping and the inertia of the orthotropic plate, the differential equation of lateral motion of an orthotropic plate on a Kerr model can be obtained as:

7

- (1 + \frac{k_{2}}{k_{1}}) (D_{x} \frac{\partial^{4} w}{\partial w^{4}} + 2 B \frac{\partial^{4} w}{\partial x^{2} \partial y^{2}} + D_{y} \frac{\partial^{4} w}{\partial y^{4}} + ρ h \frac{\partial^{2} w}{\partial t^{2}} + γ h \frac{\partial w}{\partial t} - q (x, y, t))

+ \frac{G_{s}}{k_{1}} (D_{x} (\frac{\partial^{6} w}{\partial x^{6}} + \frac{\partial^{6} w}{\partial x^{4} \partial y^{2}}) + 2 B (\frac{\partial^{6} w}{\partial x^{4} \partial y^{2}} + \frac{\partial^{6}}{\partial x^{2} \partial y^{4}}) D_{y} (\frac{\partial^{6} w}{\partial y^{6}} + \frac{\partial^{6} w}{\partial x^{2} \partial y^{2}}))

+ \frac{G_{s}}{k_{1}} (\frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}}) (ρ h \frac{\partial^{2} w}{\partial t^{2}} + γ h \frac{\partial w}{\partial t} - p (x, y, t)) = k_{2} w - G_{s} (\frac{\partial^{2} w}{\partial x^{2}} + \frac{\partial^{2} w}{\partial y^{2}}),

where $k_{1}$ is the spring stiffness of the first layer of the Kerr model, $k_{2}$ is the spring stiffness of the second layer of the Kerr model, $G_{s}$ is the shear modulus of the Kerr model, $ρ$ is the mass density of the plate, $γ$ is the structural damping ratio, and $h$ is the thickness of the plate.

In reality, loads that are caused by vehicles are often of varying amplitude. This is a because of the coarseness of rigid roadway pavement as well as the vehicle’s mechanical systems. Therefore, in practical analysis, a harmonic load model is generally used. In this study, harmonically moving a single concentrated load which is traveling with a constant velocity $v_{0}$ along the middle line is considered. Considering practical use, the dynamic load transmitted to the pavement $q (x, y, t)$ according to Eq. (7) can be expressed by using the Dirac function $δ []$ as:

8

q (x, y, t) = P_{0} (1 + α c o s ω t) δ [x - v_{0} t] δ [y - \frac{b}{2}],

where $α$ is the coefficient of the type of vehicle, $ω$ is the vibration frequency of the moving load, $b$ is the length of the orthotropic plate in the $y$ direction; $P_{0}$ is the maximum amplitude of the moving load [1].

According to Fig. 1, the effective shear force and bending moment at the orthotropic plate boundaries are given as:

9

V_{i} = D_{i} ((\frac{\partial^{3} w (x, y, t)}{\partial x^{3}}) + (\frac{B + 2 D_{t r}}{D_{i}}) (\frac{\partial^{3} w (x, y, t)}{\partial x \partial y^{2}})) = k s_{i} w (x, y, t), i = 1, . . ., 4,

10

M_{i} = - D_{i} (\frac{\partial^{2} w (x, y, t)}{\partial x^{2}} + ν_{⊥ i} \frac{\partial^{2} w (x, y, t)}{\partial y^{2}}) = k r_{i} \frac{\partial w (x, y, t)}{\partial x}, i = 1, . . ., 4 .

The constraint of the elastic vertical support and rotation are characterized by $k s_{i}$ and $k r_{i}$ , respectively. The index $i =$ 1, 2, 3, 4 stems for $x =$ 0, $a$ and $y =$ 0, $b$ , where the index notation $⊥ i$ of the Poisson’s ratio $ν$ shows the perpendicular direction of $i$ .

Fig. 1Model of the rigid road pavement on a Kerr foundation model under a dynamic moving load

3. Determination of the Eigen frequencies

The solution of the homogeneous orthotropic plate equation given by Eq. (7) can be determined by the method of variable separation using the Fourier series techniques. According to this method, the homogeneous solution of the problem is a product of function of space and time:

11

w (x, y, t) = \sum_{m = 1}^{\infty} \sum_{n = 1}^{\infty} W_{m n} (x, y) s i n (ω_{m n} t),

where $ω_{m n}$ is the undamped vibration frequency of the orthotropic plate and $W_{m n} (x, y)$ is a spatial function determined for the modal numbers $m$ and $n$ in the $x$ - and $y$ -directions. The spatial function satisfying the initial conditions of the undamped free vibration equation. The substitution of Eq. (11) into Eq. (7) yields:

12

\begin{array}{l} - (k_{1} + k_{2}) (D_{x} \frac{\partial^{4} W_{m n}}{\partial x^{4}} + 2 B \frac{\partial^{4} W_{m n}}{\partial x^{2} \partial y^{2}} + D_{y} \frac{\partial^{4} W_{m n}}{\partial y^{4}}) \\ + G_{s} (D_{x} (\frac{\partial^{6} W_{m n}}{\partial x^{6}} + \frac{\partial^{6} W_{m n}}{\partial x^{4} \partial y^{2}}) + 2 B (\frac{\partial^{6} W_{m n}}{\partial x^{4} \partial y^{2}} + \frac{\partial^{6} W_{m n}}{\partial x^{2} \partial y^{4}}) + D_{y} (\frac{\partial^{6} W_{m n}}{\partial y^{6}} + \frac{\partial^{6} W_{m n}}{\partial x^{2} \partial y^{4}})) \\ - k_{1} k_{2} W_{m n} + k_{1} G_{s} (\frac{\partial^{2} W_{m n}}{\partial x^{2}} + \frac{\partial^{2} W_{m n}}{\partial y^{2}}) \\ = ρ h {ω_{m n}}^{2} \cdot (G_{s} (\frac{\partial^{2} W_{m n}}{\partial x^{2}} + \frac{\partial^{2} W_{m n}}{\partial y^{2}}) - (k_{1} + k_{2}) W_{m n}) . \end{array}

Since $W_{m n} (x, y)$ in Eq. (12) depends only on the spatial variables and the orthotropic plate vibrates with the same temporal behavior, each side of Eq. (12) must be equal to the arbitrary separation constant. A relationship between the undamped vibration frequencies of the orthotropic plate and the arbitrary separation constant $κ_{m n}$ can be expressed as [1]:

13

{ω_{m n}}^{2} = (\frac{κ_{m n}}{ρ h}) \frac{- k_{1}}{[G_{s} ({(\frac{p π}{a})}^{2} + {(\frac{q π}{b})}^{2}) + (k_{1} + k_{2}) W (x, y)]} = (\frac{κ_{m n}}{ρ h}) Ψ,

where:

14

\begin{array}{l} κ_{m n} = - (\frac{k_{1} + k_{2}}{k_{1}}) (D_{x} \frac{p^{4} π^{4}}{a^{4}} + 2 B \frac{π^{4} p^{2} q^{2}}{a^{2} b^{2}} + D_{y} \frac{q^{4} π^{4}}{b^{4}}) - k_{2} - G_{s} k_{1} (\frac{p^{2} π^{2}}{a^{2}} + \frac{q^{2} π^{2}}{b^{2}}) \\ - \frac{G_{s}}{k_{1}} [D_{x} (\frac{p^{6} π^{6}}{a^{6}} + \frac{π^{6} p^{4} q^{2}}{a^{4} b^{2}}) + 2 B (\frac{p^{4} q^{2} π^{6}}{a^{4} b^{2}} + \frac{π^{6} p^{2} q^{4}}{a^{2} b^{4}}) + D_{y} (\frac{q^{6} π^{6}}{b^{6}} + \frac{π^{6} p^{2} q^{4}}{a^{2} b^{4}})] . \end{array}

Based on the modified Bolotin method, the two unknowns real numbers $p$ and $q$ in Eqs. (13), (14) can be solved from the two auxiliary Levy’s type problems [15].

4. Determination of the Eigen modes of the orthotropic plate

4.1. First auxiliary Levy problem

The solution of Eq. (12) for the first auxiliary problem that satisfies the boundary conditions defined in Eqs. (9), (10) can be assumed as:

15

W_{m n} (x, y) = X_{m n} (x) s i n (\frac{q π}{b} y),

where $X_{m n} (x)$ is the Eigen mode of the orthotropic plate in the $x$ -direction [15]. Substituting Eq. (15) into Eq. (12) which results in an ordinary differential equation for $X_{m n} (x)$ in which the solution of the characteristic equation can be found by assuming $X_{m n} (x) = e^{β x}$ . By substituting $X_{m n} (x) = e^{β x}$ into the characteristic equation we found the sixth order characteristic equation of $β$ which has two imaginary roots and two real double roots. The solution of the first auxiliary problem can be expressed as:

16

\begin{array}{l} X_{m n} (x) = A_{1} c o s (\frac{p π}{a} x) + A_{2} s i n (\frac{p π}{a} x) + A_{3} (\frac{β π}{a} x + 1) c o s h (\frac{β π}{a} x) \\ + A_{4} (\frac{β π}{a} x + 1) s i n h (\frac{β π}{a} x) . \end{array}

Boundary conditions along the $x$ -axis permit determining the $A_{i}$ coefficients from [16, 17]:

17

a_{i j} A_{i} = 0, i = j = 1, . ., 4,

where $a_{i j}$ are the coefficients.

When the conditions of the boundary along $x =$ 0 and $x = a$ in Eqs. (9), (10) are substituted into Eq. (16), the characteristic determinant of $D e t [A] = |a_{i j}| =$ 0 leads to the existence of nontrivial solutions. After expanding resulted in the first transcendental equation in terms of $p$ and $q$ .

The second auxiliary Levy problem in the $y$ -axis can be determined analogously to the above formulations.

4.2. Mode numbers

The determinants of the first and second auxiliaries Levy problems, being transcendental in nature, have an infinite number of roots. The Mathematica software [18] was used to solve the values of $p$ and $q$ symbolically. By substituting the values of $p$ and $q$ into Eq. (13), the Eigen frequencies of the system can be obtained. The integer parts of $p$ and $q$ represent the number of mode in the system. The mode shapes of the system are therefore given by:

18

W (x, y) = \sum_{m = 1}^{\infty} \sum_{n = 1}^{\infty} X_{m n} (x) Y_{m n} (y) .

5. Determination of the non-homogeneous solution of the system

Since a fundamental set of solutions of the homogenous partial differential equation is known and given by Eq. (18), a non-homogeneous solution of the system can be found by replacing the unknown constant coefficients in Eq. (16) in the $x$ direction as well as in the $y$ direction with unknown coefficient functions. The appropriate solution for the forced response can be expressed in the form:

19

w (x, y, t) = \sum_{m = 1}^{\infty} \sum_{n = 1}^{\infty} X_{m n} (x) Y_{m n} (y) T_{m n} (t),

where $X_{m n} (x)$ and $Y_{m n} (y)$ are the mode shapes of the system, $T_{m n} (t)$ depends only on the temporal variable and can be determined from the non-homogeneous partial differential equation of time. From the natural frequency $ω_{m n}$ computed by Eq. (13), depending on the first and second spring stiffness and the shear moduli of the Kerr foundation, the temporal equation of $T_{m n} (t)$ can be stated in [19] as follow:

20

\begin{array}{l} {\ddot{T}}_{m n} (t) + 2 ζ ω_{m n} T_{m n} (t) + ω_{m n}^{2} T_{m n} (t) \\ = \frac{Ψ}{ρ h Q_{m n}} \int_{0}^{a} X_{m n} (x) d x \int_{0}^{b} Y_{m n} (y) d y \cdot (\frac{G_{s}}{k_{1}} (\frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}}) - \frac{k_{1} + k_{2}}{k_{1}}) p (x, y, t), \end{array}

where $ζ$ is the damping ratio of the system and $Q_{m n}$ is a normalization factor expressed by:

21

Q_{m n} = \int_{0}^{a} {(X_{m n} (x))}^{2} d x \int_{0}^{b} {(Y_{m n} (y))}^{2} d y .

The corresponding homogeneous solution of Eq. (20) can be written:

22

T_{0 m n} (t) = e^{- ζ ω_{m n} t} (a_{m n} c o s (ω d_{m n} t) + b_{m n} s i n (ω d_{m n} t)) .

From the stationary state initial conditions ( $t =$ 0 s), $T_{0 m n} (t) = a_{m n} = b_{m n} =$ 0 can be obtained. A particular and a general solution of Eq. (20) may be integrated to determine the temporal response of the problem for an arbitrary applied surface load [1]:

23

\begin{array}{l} T_{m n} (t) = \int_{0}^{t} [\frac{Ψ}{ρ h Q_{m n} \sqrt{1 - ζ^{2}} ω_{m n}} \int_{0}^{a} X_{m n} (x) d x \int_{0}^{b} Y_{m n} (y) d y \\ {\cdot e}^{- ζ ω_{m n} (t - τ)} (\frac{G_{s}}{k_{1}} (\frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}}) - \frac{k_{1} + k_{2}}{k_{1}}) q (x, y, τ) s i n ω d_{m n} (t - τ)] d τ . \end{array}

Finally, the deflection solution of the governing Eq. (7) subjected to an arbitrary applied dynamic surface load $q (x, y, t)$ for 0 $\leq t \leq t_{0}$ and $t > t_{0}$ can be expressed as

For 0 $\leq t \leq t_{0}$ :

24

w (x, y, t) = \sum_{m = 1}^{\infty} \sum_{n = 1}^{\infty} X_{m n} (x) Y_{m n} (y) \int_{0}^{t} [\frac{ψ}{p h Q_{m n} \sqrt{1 - ζ^{2} ω_{m n}}} \int_{0}^{a} X_{m n} (x) d x

\cdot \int_{0}^{b} Y_{m n (y) d y} e^{- ζ ω_{m n (t - τ)}} (\frac{G_{s}}{k_{1}} (\frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}}) \frac{k_{1} + k_{2}}{k_{1}}) q (x, y, τ) s i n ω d_{m n} (t - τ)] d τ .

For $t > t_{0}$ :

25

w (x, y, t) = \sum_{m = 1}^{\infty} \sum_{n = 1}^{\infty} e^{- ζ ω_{m n} (t - t_{0})} [w_{0 m n} c o s \{ω d_{m n} (t - t_{0})\} + \frac{v_{0 m n} + ζ w_{0 m n}}{ω d_{m n}} s i n ω d_{m n} (t - t_{0})] .

In which $w_{0 m n}$ and $v_{0 m n}$ are the deflection and velocity at the time $t = t_{0}$ , respectively and $ω d_{m n} = \sqrt{1 - ς^{2}} ω_{m n}$ .is the damped vibration frequency of the orthotropic plate.

6. Numerical examples

Using the procedure described above, a rigid rectangular orthotropic plate doweled of road pavement subjected to dynamic traffic loads as shown in Fig. 1 is analyzed. The values of parameters which are used in the following examples are given as: $a =$ 5 m, $b =$ 3.5 m, $h =$ 0.25 m, $E_{x} =$ 27×10⁹ Pa, $E_{y} =$ 22.5×10⁹ Pa, $ρ =$ 2.5×10³ kg/m³, $ν_{x} =$ 0.180, $ν_{y} =$ 0.150, $k s_{x 1} = k s_{x 2} = k s_{y 1} = k s_{y 2} =$ 150 MN/m/m, $k r_{x 1} = k r_{x 2} = k r_{y 1} = k r_{y 2} =$ 1 N·m/rad/m. Three types of soil condition are considered in this work: soft soil $k_{1} = k_{2} =$ 27.25 MN/m³, $G_{s} =$ 9.52 MN/m³; medium soil $k_{1} = k_{2} =$ 54.4 MN/m³, $G_{s} =$ 19.04 MN/m³and hard soil $k_{1} = k_{2} =$ 108 MN/m³, $G_{s} =$ 38.08 MN/m³. These parameters are typical of the material and structural properties of a highway [19]. The traffic load magnitude is $P_{0} =$ 80×10³ N and $α =$ 1/2. To calculate the influence of loading velocity to the dynamic behavior of the system, $v$ varies from 50 km/hr to 300 km/hr. It is also assumed that damping ratio of the system equals $ζ =$ 5 %. To compare the dynamic deflections of the orthotropic plate between the Pasternak and the Kerr foundation models, the following soil parameters are used: $G_{s} =$ 9.52 MN/m³; $k =$ 27.25 MN/m³. All the dynamic response of the system is computed at $t =$ 1.5 s. This is the condition at which the dynamic moving load is within the plate region.

6.1. Influence of the foundation types

Time history of the dynamic deflection at the center of the plate $w (a / 2, b / 2)$ , is calculated and plotted for $m =$ 1, 2, 3, …, 5 and $n =$ 1, 2, 3, …, 4. It is found that the dynamic deflection of the system is initially high, with rapid oscillations and high amplitudes for all three types of soil conditions studied in this paper. This observation is in agreement with Gibigaye et al. in the design of pavement plates rest on a soil whose inertia is considered [17].

Fig. 2(a) shows time histories of the system under dynamic moving load for soft soil and hard soil conditions of the Kerr foundation. The moving dynamic load is set to be $v =$ 60 km/hr and load frequency is $ω =$ 100 rad/s. It is observed that the rapid oscillations occur at the moment of first loading and after the oscillations become stationary for two types of soil condition. In Fig. 2(a), it is also shown that the transient domain ends at around $t =$ 0.06 s and does not depend on the soil conditions. This trend was also observed in [17].

Fig. 2(b) shows the time history of the system supported by the Kerr foundation model and Pasternak foundation model. To generalize the Pasternak model, the Kerr model is introduced by adding a layer of spring on the shearing layer to eliminate the concentrated reactions that occurs along the free edges of a plate structure [13].

Fig. 2Time history of the system under dynamic moving load

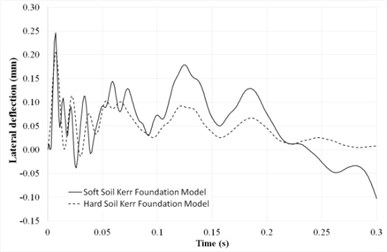
a) Two soil conditions on Kerr foundation

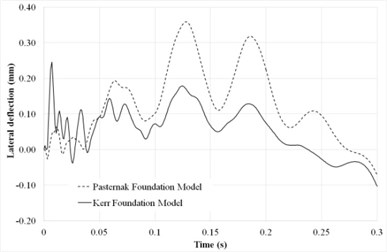
b) Kerr and Pasternak foundations

From Fig. 2(b), it is found that the maximum dynamic deflection of the system supported by the Kerr foundation is lower than the maximum dynamic deflection of the system on the Pasternak foundation model at the mid-span if calculated with the same parameters [20]. This result agrees with previous research done by Kneifati [13], where it was shown that the Kerr model is more accurate than the Pasternak models for the representation of the base response.

6.2. Influence of moving load on the maximum dynamic deflection

Fig. 3(a) depicts the maximum dynamic deflections of the plates which are subjected to a moving load with the harmonic load frequency is $ω =$ 100 rad/s and soil condition is set to the parameter values for soft and medium soil conditions of the Kerr foundation. It can be observed that the speed of the dynamic load has an effect on the maximum lateral dynamic deflection. The maximum dynamic deflection at the lower value of foundation stiffness increases until about $v =$ 240 km/hr before decreasing. It shows that resonance conditions depend both on the speed of travel and the stiffness constants of the foundation.

Fig. 3(b) illustrates the effects of load frequency on the maximum lateral deflection under moving load for soft soil and hard soil conditions. It can be seen that load frequency has effects on both the resonance frequency and the maximum lateral deflection. The resonance load frequency for soft soil condition is smaller than the value of resonance load frequency for the hard soil condition.

Fig. 3Maximum dynamic deflection of the rigid road pavement subjected to moving load

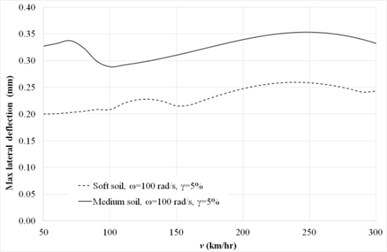
a) Speeds at harmonic frequency ( $ω =$ 100 rad/s)

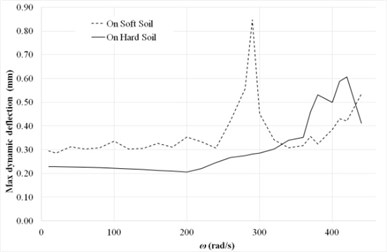
b) Load frequencies at moving load ( $v =$ 60 km/hr)

7. Conclusions

The responses behaviors of rigid road pavements that are subjected to dynamic moving loads with constant velocity have been investigated. The effects of moving velocity, load frequency and elastic foundation stiffness of the Kerr model are studied. The soil model used in this work is the Kerr model; a proposed generality of the Pasternak model by the inclusion of a layer of springs on the shearing layer. Based on the orthogonality properties of the Eigen functions, the semi-analytical solution form of the dynamic displacement was obtained. In the formulation of this paper, it was assumed that the supports at the boundaries of the plate are due to the tie bars and steel dowels, providing the plate with vertical and rotational restraints. This assumption represents a realistic plate, especially for joints between the rigid pavement plates, in which rotation and vertical shear deformation are found along the joints.

From these results, it is concluded the dynamic response and resonance velocity is significantly affected by the elastic foundation stiffness. When the rigid road pavement rests on a soft soil foundation, most of the pavement is affected by the loading while the resonance load frequency is small. From the obtained results, it is also concluded that the maximum dynamic deflection of the rigid road pavement on the Kerr model decreases significantly compared to that of Pasternak model. This result shows the possible economic gain of the Kerr model when it is used for representing the base response of the rigid road pavement.

References

Alisjahbana S. W., Wangsadinata W. Dynamic analysis of rigid road pavement under moving traffic loads with variable velocity. Interaction and Multiscale Mechanics, Vol. 5, Issue 2, 2012, p. 105-114.

Publisher
Westergaard H. M. Stresses in Concrete Pavements Computed by Theoretical Analysis. Federal Highway Administration, Vol. 7, Issue 2, 1926, p. 25-35.

Search CrossRef
Rahman S. O., Anam I. Dynamic analysis of concrete pavement under moving loads. Journal of Civil and Environmental Engineering, Vol. 1, Issue 1, 2005, p. 1-6.

Search CrossRef
Yang T. Y. A Finite element analysis of plates on a two parameter foundation model. Computers and Structures, Vol. 2, Issue 4, 1972, p. 593-614.

Publisher
Zhi Y. A., Jian B. C. Static interaction analysis between a Timoshenko beam and layered soils by analytical layer element/boundary element. Applied Mathematical Modelling, Vol. 40, Issues 21-22, 2016, p. 9485-9499.

Publisher
Trinh T. H., Nguyen D. K., Gan B. S., Alexandrov S. Post-buckling responses of elastoplastic FGM beams on nonlinear elastic foundation. Structural Engineering and Mechanics, Vol. 58, Issue 3, 2016, p. 515-532.

Publisher
Nguyen D. K., Trinh T. H., Gan B. S. Post-buckling response of elastic-plastic beam resting on an elastic foundation to eccentric axial load. The IES Journal Part A: Civil and Structural Engineering, Vol. 5, Issue 1, 2012, p. 43-49.

Search CrossRef
Taheri M. R., Zaman M., Alvappillai A. Dynamic response of concrete pavements to moving aircraft. Applied Mathematical Modelling, Vol. 14, Issue 11, 1990, p. 562-575.

Publisher
Zaman M., Taheri M. R., Alvappillai A. Dynamic analysis of thick plates on viscoelastic foundation to moving loads. International Journal of Numerical and Analytical Methods in Geomechanics, Vol. 15, Issue 9, 1991, p. 627-647.

Publisher
Patil V. A., Sawant V. A., Deb K. 2-D finite element analysis of rigid pavement considering dynamic vehicle-pavement interaction effects. Applied Mathematical Modelling, Vol. 37, Issue 3, 2013, p. 1282-1294.

Publisher
Gan B. S., Nguyen D. K. Large Deflection Analysis of Functionally Graded Beams Resting on a Two-Parameter Elastic Foundation. Journal of Asian Architecture and Building Engineering, Vol. 13, Issue 3, 2014, p. 649-656.

Publisher
Paliwal D. N., Ghosh S. K. Stability of orthotropic plates on a Kerr foundation. American Institute of Aeronautics and Astronautics Journal, Vol. 38, Issue 10, 2000, p. 1994-1997.

Publisher
Kneifati M. C. Analysis of plates on a Kerr foundation model. Journal of Engineering Mechanics, Vol. 111, Issue 11, 1985, p. 1325-1342.

Publisher
Limkatanyu S., Prachasaree W., Damrongwiriyanupap N., Kwon M., Jung W. Exact stiffness for beams on Kerr-Type Foundation: The Virtual Force Approach. Journal of Applied Mathematics, p. 2013-626287.

Search CrossRef
Kerr A. D. Elastic and viscoelastic foundation models. Journal of Applied Mechanics, Vol. 31, Issue 3, 1964, p. 491-498.

Publisher
Pevzner P. Further modification of Bolotin method in vibration analysis of rectangular plates, American Institute of Aeronautics and Astronautics Journal, Vol. 38, Issue 9, 2000, p. 1725-1729.

Publisher
Alisjahbana S. Dynamic response of clamped orthotropic plates to dynamic moving loads. Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, Canada, 2004.

Search CrossRef
Gibigaye M., Yabi C. P., Alloba I. E. Dynamic response of a rigid pavement plate based on an inertial soil. International Scholarly Research Notices, Vol. 2016, 2016, p. 4975345.

Publisher
Wellin P., Gaylord R., Kamin S. An Introduction to Programming with Mathematica. 3rd Edition, Cambridge University Press, 2005.

Publisher
Baadilla D. A. Dynamic Response of Orthotropic Plate on the Kerr Foundation. Master thesis, Universitas Tarumanagara, Jakarta, Indonesia, 2001, (in Indonesian).

Search CrossRef
Husada A. The Effect of Vehicle Speed on the Dynamic Response of Rigid Pavement Structure. Master Thesis, Universitas Tarumanagara, Jakarta, Indonesia, 2016, (in Indonesian).

Search CrossRef

Cited by

Deformation Pattern of Beams Rested on Different Foundation Models in Nonuniform Foundation Conditions

Huanzhu Zhou | Yanning Wang | Weiming Huang | Jun-jie Zheng | Qixin Wu

(2024)

Mechanical Analysis of the Stress State and Damage Risk of Asphalt Pavement Based on a Three-Dimensional Space Calculation Program

Dayong Jiang | Dongsheng Wang | Zhongshi Pei | Decheng Feng | Junyan Yi

(2023)

Dynamic deflection of concrete plate in semi-rigid supports and various damping condition

Yenny Untari Liucius | Sofia W. Alisjahbana

(2019)

Free vibration of a Levy-type solution for plates based on two-variable refined plate theory by using SEM

Shota Kiryu | Sofia W. Alisjahbana | Irene Alisjahbana | Mitsuo Nagao | Buntara S. Gan

(2019)

About this article

Received

21 March 2018

Accepted

17 July 2018

Published

15 August 2018

SUBJECTS

Vibration in transportation engineering

DOI

https://doi.org/10.21595/jve.2018.20082

Keywords

rigid road pavement

dynamic traffic loads

Kerr foundation

transcendental equation

modified Bolotin method

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2020 05 15

Two-span bridge under moving load – numerical and experimental approach

Veronika Valašková, Daniela Kuchárová, Jozef Melcer

Research article

2019 08 15

Numerical simulation of vehicle movement on rigid roadway pavement with discontinuities

Sofia W. Alisjahbana, Ade Asmi, Safrilah, Jouvan Chandra Pratama Putra, Buntara S. Gan, Irene Alisjahbana

Research article

2018 12 31

Some possibilities of modeling of moving load on concrete pavements

Veronika Valsšková, Jozef Melcer

Research article

2017 08 15

Dynamic response of water saturated subgrade surface layer under high speed train using moving element method

Bao Liu, Qian Su, Ting Liu, Ting Li

S. W. Alisjahbana, I. Alisjahabana, S. Kiryu, and B. S. Gan, “Semi analytical solution of a rigid pavement under a moving load on a Kerr foundation model,” Journal of Vibroengineering, Vol. 20, No. 5, pp. 2165–2174, Aug. 2018, https://doi.org/10.21595/jve.2018.20082

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2018.20082
UR  - https://doi.org/10.21595/jve.2018.20082
TI  - Semi analytical solution of a rigid pavement under a moving load on a Kerr foundation model
T2  - Journal of Vibroengineering
AU  - Gan, Buntara S.
AU  - Alisjahbana, Sofia W.
AU  - Alisjahabana, Irene
AU  - Kiryu, Shota
PY  - 2018
DA  - 2018/08/15
PB  - JVE International Ltd.
SP  - 2165-2174
IS  - 5
VL  - 20
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Gan_2018,
	doi = {10.21595/jve.2018.20082},
	url = {https://doi.org/10.21595/jve.2018.20082},
	year = 2018,
	month = {aug},
	publisher = {{JVE} International Ltd.},
	volume = {20},
	number = {5},
	pages = {2165--2174},
	author = {Buntara S. Gan and Sofia W. Alisjahbana and Irene Alisjahabana and Shota Kiryu},
	title = {Semi analytical solution of a rigid pavement under a moving load on a Kerr foundation model},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]B. S. Gan, S. W. Alisjahbana, I. Alisjahabana, and S. Kiryu, “Semi analytical solution of a rigid pavement under a moving load on a Kerr foundation model,” Journal of Vibroengineering, vol. 20, no. 5, pp. 2165–2174, Aug. 2018, doi: 10.21595/jve.2018.20082.

Copy IEEE

Copied to clipboard!

Gan, Buntara S., Sofia W. Alisjahbana, Irene Alisjahabana, and Shota Kiryu. “Semi Analytical Solution of a Rigid Pavement under a Moving Load on a Kerr Foundation Model.” Journal of Vibroengineering 20, no. 5 (August 15, 2018): 2165–74. https://doi.org/10.21595/jve.2018.20082.

Copy Chicago

Copied to clipboard!

Semi analytical solution of a rigid pavement under a moving load on a Kerr foundation model

Abstract

1. Introduction

2. Governing equation

3. Determination of the Eigen frequencies

4. Determination of the Eigen modes of the orthotropic plate

4.1. First auxiliary Levy problem

4.2. Mode numbers

5. Determination of the non-homogeneous solution of the system

6. Numerical examples

6.1. Influence of the foundation types

6.2. Influence of moving load on the maximum dynamic deflection

7. Conclusions

References

Cited by

About this article

Related Articles