Methodology for identification of liquid concentration in the periodic microstructures applying numerical-experimental laser interferometric methods

1. Introduction

The main component of a lab-on-a-chip is periodic microstructure. Micro channels (periodic microstructures) are used for the fluid transportation, mixing, separation and other processing. The set of micro channels are being formed by soft-lithography [1], photo polymerisation [2, 3], holographic lithography [4], laser ablation [5], micro-injection moulding [6, 7], phase separation [8], gas foaming [9] or 3D printing [10] using a wide range of materials such as polydimethylsiloxane, silicon, polycarbonate, glass, rubber, aluminium and others [11-13]. Usage of new materials such as piezoelectric nanocomposite allows to develop new periodic microstructure with new features like piezoelectric properties or specific optical characteristics. Control methods of micro fluidics by applying acoustic manipulation are known in the world. For this purpose, standing and travelling waves are excited in micro channels [14]. The generated walls of micro hydro dynamical systems are excited by vibration methods which ensure more effective flow of micro fluids [15]. Thin PZT films integrated into micro dynamical systems ensure more effective functionality [16].

The investigation of the high frequency vibrations of the fluid is an important problem in the design of microfluidic devices. Laser interferometric methods such as time average holography, high speed double expose holography or laser light diffraction allow to do analysis of high speed fluid flow and dosing or vibration of micro components used in biological and chemical microsystems. Therefore, methodology for identification of liquid concentration in the periodic microstructures applying numerical-experimental laser interferometric methods is proposed in this paper.

2. Main equations of holography for phase object investigation

The two-dimensional flow of the ideal compressible liquid in the microchannel (depth is $h$) is illuminated by laser (wavelength – $\lambda$). The phase shift of the light of the lasers’ beam which goes through the fluid is [17]:

where $n_S$ is the fluids’ refractive index in static condition and $n_{flow}$ in flow. The refractive index of the liquid in flow condition depends on the dynamic ${\rho }_{flow}\left(x,y,t\right)$ and static ${\rho }_s$ densities and could be expressed as:

where correction coefficient $\beta$ should be determined from experiments.

If time average hologram is recorded of that light during a time interval $T\gg 1/\omega$, than phase factor of the reconstructed wave is proportional to:

The intensity of the observed interference pattern is proportional to:

Also, it is possible to use hi speed double exposure holography for the fluid flow analysis if the flow varies steadily and the exposure time is $T\ll 1/\omega$. Than it could be assumed that density field is constant during the exposure. For this case interference pattern is proportional to:

where $\stackrel{-}{\phi }(x,y)$ is the change in phase between the two exposures.

3. Determination of liquids’ concentration

For the development of methodology for identification of liquid concentration in the periodic microstructures applying numerical-experimental laser interferometric methods is selected periodic microstructure (period 4 μm, depth 0.7 μm) made from aluminum and polycarbonate and three liquids (pure water, acetone and glycerol). Optical properties of the selected materials illuminated by red laser ($\mu =$ 633 nm) are presented in Table 1.

Optical properties of the microfluidic are investigated by non-destructive optical laser diffractometer (Fig. 1). He-Ne laser diffractometer ($\lambda =$ 633 nm) was used in order to register intensities of reflected or transmitted diffraction maxima efficiencies. All liquids are characterized by relative diffraction efficiencies. Relative diffraction efficiency RDE is defined as ratio of intensity of diffracted light to the $i$th diffraction maxima (0, ±1, ±2, …) with intensity of the reflected light from the surface without micro relief [18]. Liquids’ refractive index is determined from comparison of theoretical and experimental diffraction efficiencies. As it is stated in Section 2 liquid density could be calculated from the measured refractive index.

Fig. 1Measuring schema of diffraction maxima: 1 – sample, 2 – photodiode, 3 – ampere meter, 4 –maxima distribution

The diffraction efficiencies of the microfluidic illuminated by laser are calculated theoretically employing commercial software GSolver V5.2 (Fig. 2). GSolver is based on the modal method. It is set up to work with linear isotropic homogeneous materials and is a full vector implementation of a class of algorithms known as Rigorous Coupled Wave (RCW) analysis.

Fig. 2Software GSolver V5.2 for calculation of optical parameters of microfluidics

4. Results

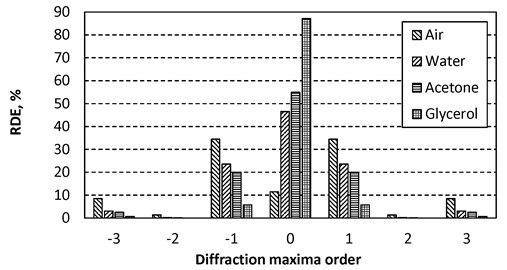
Two periodic microstructure fabricated in aluminum (Al) and polycarbonate (PC) were investigated numerically and experimentally with three liquids (pure water, acetone and glycerol) in order to identify sensitivity of the proposed method. For the measurement of diffraction maxima of the reflected light Al microstructure was used while maxima of the transmitted light were investigated with PC microstructure. Relative diffraction efficiencies of the transmitted and reflected light with three liquids and in air are presented in Fig. 3, 4.

Diffraction efficiencies of the periodic microstructures without an analyte (in air or vacuum) show that periodic microstructure (period 4 μm, depth 0.7 μm) was designed for operation in transmitting mode, i.e. first order diffraction maxima are three times higher in transmitting mode than reflecting. Therefore, periodic microstructure in transmitting mode is more sensitive to refractive index (density) of the analyte. Refractive index change from 1.33 (pure water) to 1.47 (glycerol) leads the decrease of the first order maxima diffraction efficiency four times from 24 % to 6 % (Fig. 4). At the same time reflecting microstructure is not sensitive enough. Results confirm the idea of liquid concentration identification in the periodic microstructures applying numerical-experimental laser interferometric methods.

Fig. 3Relative diffraction efficiencies of the transmitted light through PC periodic microstructure

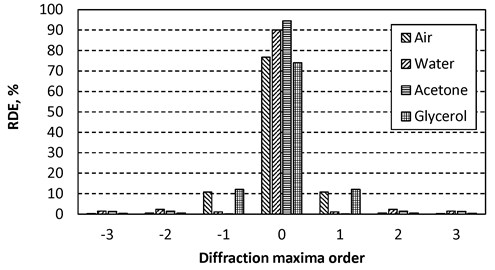
Fig. 4Relative diffraction efficiencies of the reflected light from Al periodic microstructure

5. Conclusions

Liquids’ refractive index and density in flow condition could be determined from comparison of theoretical and experimental diffraction efficiencies. Change of refractive index by 0.008 increases or decreases diffraction efficiency of the first order diffraction maxima by 1 %. Non-uniform distribution of the fluid density could be determined using holographic methods. Harmonic variation of the fluid density could be registered using time average or high speed double exposure holography.