To the modeling of processes with repeated damped collisions

1. Introduction

In the general case, regimes with repeated collisions (modes with bounce or chatter) can be called movements accompanied by many collisions of contacting solids after the first impact occurred. In the simplest case, this phenomenon consists in the known effect of the bobbing of a coin, which at a certain height was released above a massive metal or stone slab. From a mechanical point of view, a bounce occurs when the colliding bodies are in a field of forces that return them to the point of contact, resulting in repeated collisions.

It is known that in several cases, the bounce of contacts can cause great damage to technical objects. It can occur and occurs in numerous electromechanical switching devices, as well as in the components of various systems - buttons, relays, reed switches, contactors, magnetic starters and so on. The effect is manifested in the fact that after the first connection numerous repeated disconnects and closures of the contacts are observed.

This significantly reduces the reliability of devices, introduces undesirable distortions into their work and can lead to premature failures and loss of operability of equipment elements. For example, the commutation of powerful electric circuits can be accompanied by ignition and extinction of the electric arc and the appearance of sparks, which causes rapid contact wear.

The most important characteristics of the bounce are impulses of impacts, the number of collisions from the beginning of the first contact to the last, and the duration (time) of the bounce. These parameters depend on the design parameters of the systems. Bounce times range from order values of 1 to 2 microseconds from modern miniature reed switches to hundreds of milliseconds in powerful contactors.

The methods used to combat bounce are based on hardware and algorithmic techniques. Their description is widely presented on the Internet, due to the very wide distribution of devices related to the Arduino platform [1]. Basically, these methods are palliative, do not consider the mechanics of processes and cannot be completely effective. Mathematical modeling of electromechanical contacts or similar systems, apparently, was first conducted by L. Mandelstam [2]. It should be noted the work of R. Nagaev [3], who gave complete and detailed descriptions of regimes with repeated collisions for several nontrivial mechanical problems.

In this paper, we consider some model problems and methods for describing the chatter by means of the averaging technique.

2. Modeling approach

A typical example of contact systems of this type is shown in Fig. 1.

Fig. 1The electronic control relay “PMDsrange” of the company “Pilz International”, Germany

As the main working model, we take the system shown in Fig. 2(a). At the ends of elastic weightless beams (springs), colliding point bodies with masses $m_1$ and $m_2$ [4] are fixed. The assumption that bodies are pointlike means that all their geometric parameters can be neglected in comparison with the gap size $\mathrm{\Delta }\ge$ 0 (negative values $\mathrm{\Delta }$ correspond to the preload).

Fig. 2The main working model

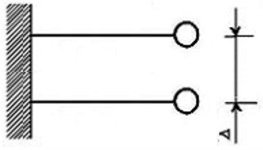
a)

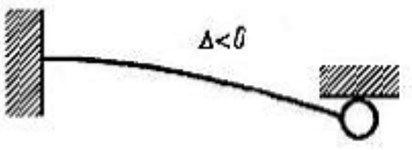
b)

The equations of motion of the system in the absence of constantly acting external excitation forces are obviously of the form:

where $x_1$ and $x_2$ are the coordinates of the colliding bodies; $x=x_1-x_2$. Collisions occur at $x=\mathrm{\Delta }$. We denote by $B_1(p;x_1)$ and $B_2(p;x_1)$ operator functions describing the energy dissipation in systems without considering the energy loss during impacts ($p\equiv d/dt$). Here, not only the standard factors leading to the use of viscous friction models can be taken into account, but also the circumstances associated with internal imperfections and peculiarities of the material of the beams (springs). For example, they can be made from materials with relaxation. In Eq. (1) the function $\mathrm{\Phi }(x,\dot{x})$ denotes the impact force, which depends on the relative coordinate and velocity. Let the impact be modeled according to Newton. Then at the instant of impact $t=t_{\alpha }$ we have $\dot{x}(t_{\alpha }-0)=-R\dot{x}(t_{\alpha }+0)$; 0 $<R\le$ 1 and $\mathrm{\Phi }(x,\dot{x})={\mathrm{\Phi }}_0(x,\dot{x})+(1-R){\mathrm{\Phi }}_1(x,\dot{x})$. Here, the elastic [${\mathrm{\Phi }}_0$] and dissipative [${\mathrm{\Phi }}_1$] components of the impact force, written through a generalized function. For each impact [5]: $\mathrm{\Phi }{|}_{t=t_{\alpha }}=J\delta (t-t_{\alpha });J=(1+R)\left|\dot{x}\right(t_{\alpha }-0\left)\right|$, where $J$ is impact impulse; $\delta \left(t\right)$ is Dirac $\delta$-function; $t_{\alpha }$ is the moment of some impact; 0 $<R\le$ 1 is restitution ratio.

In practice, many commutation systems in which bounce occurs have a regular or quasiregular structure, that is, for our model $m_1\approx m_2$, $c_1\approx c_2$, $B_1\approx B_2.$ Let the operators $B_1$, $B_2$ be linear, then from Eq. (1) after the calculations we find for the relative coordinate:

Here $\frac{1}{2}m=m_1=m_2$, $\frac{1}{2}{c}_{}=c_1=c_2$, $\frac{1}{2}B=B_1=B_2$; $1-R\equiv r$; $\epsilon$ is a small parameter (we consider quasi-conservative models). If $m_1\gg m_2$, the model is analogous: we can assume that $m{}_1{}^{\mathrm{}}\mathrm{}\to \mathrm{\infty }$ and the problem reduces to an analysis of the impact oscillator interacting with a fixed limiter (see Fig. 2(b), $\mathrm{\Delta }<$ 0).

3. Method of analysis

We analyze Eq. (2) using the averaging technique in form, which in respect of vibro-impact systems was developed in books [5]. The solution of the problem for the conservative case $\epsilon =$ 0 is well known and studied. It is described by expressions:

Here $\mathrm{\Omega }=\sqrt{c{m}^{-1}}$ is natural frequency of a linear oscillator; $T=\text{2}\pi {\omega }^{-1}$ is the process period. The second formula in Eq. (3) is valid only for 0 $<t\le T$. If the variable $t$ lies outside this interval, then it is necessary to use the conditions of periodicity or the representation of the solution in the form of a Fourier series [5]. The impact impulse $J$ is nonnegative. In a conservative system, it is determined from the impact condition $x\left(0\right)=\mathrm{\Delta }$. In an autonomous system, we can assume that the moment of impact coincides with the beginning of the time count.

We make the transition to the new variables “impulse -phase” $(x,\dot{x})\to (J,\psi )$ in accordance with formulas $x=-J\chi [\psi ,\omega (J\left)\right],\dot{x}=-J\omega \left(J\right){\chi }_{\psi }[\psi ,\omega (J\left)\right]$. In this case, the dependence of $\omega \left(J\right)$ is determined from the fourth formula Eq. (3). In this case, we choose if $\mathrm{\Delta }>$ 0, $\mathrm{\Omega }<\omega <\text{2}\mathrm{\Omega }$, if $\mathrm{\Delta }\le$ 0, $\text{2}\mathrm{\Omega }<\omega <\mathrm{\infty }$, if $\mathrm{\Delta }=$ 0, $\omega =\text{2}\mathrm{\Omega }$ (see [5]). After the transformations, the following equations can be obtained for the new variables:

Here ${\delta }^{2\pi }\left(\psi \right)$ is a generalized 2$\pi$-periodic $\delta$ – function. To determine a slowly changing evolutionary component of the process, it is enough to average Eq. (4) over the fast phase. Let the initial conditions look like this: $x\left(0\right)=\mathrm{\Delta }$, $J=J_0>$ 0. Averaging Eq. (4), after a series of calculations, one can obtain:

In the first approximation, Eq. (5) is not used [6]. Now considering various dissipation models it is possible to estimate the regime parameters with repeated damped collisions.

4. Results and discussion

Let's break down several important examples. First, let $B=$ 0 and on the process only affect the energy loss in collisions ($R<$ 1). Using the third relation Eq. (3), we find for $\mathrm{\Delta }>0$, $(\mathrm{\Omega }<\omega <2\mathrm{\Omega })$$\dot{J}=-\frac{1}{2}\epsilon rJ\mathrm{\Omega }{\left\{\pi -\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{g}\left[\frac{J}{2\mathrm{\Omega }\mathrm{\Delta }}\right]\right\}}^{-1}$. The only stationary regime corresponds to the termination of collisions (the impact pulse is zero): $J=J_0=$ 0. This regime is asymptotically stable, since for a small perturbation of the stationary regime ($\delta J_0$) the equation in variations and its solution take the form: $\delta \dot{J}=-\frac{1}{2}\epsilon r\mathrm{\Omega }\delta J$, $\delta J=\delta J_0\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{1}{2}\epsilon r\mathrm{\Omega }t\right)$. So, the time of returning to the undamped free sinusoidal oscillations (the time of termination of the vibro-impact process, with a bounce) is infinite in such a model.

For a system with preload ($\mathrm{\Delta }<$ 0, $\text{2}\mathrm{\Omega }<\omega <\mathrm{\infty }$), Eq. (6) takes the form ($B=$ 0).

$\dot{J}=-\frac{1}{2}\epsilon rJ\mathrm{\Omega }{\left\{\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{g}\left[\frac{J}{2\mathrm{\Omega }\mathrm{\Delta }}\right]\right\}}^{-1}$. In this case, there is no stationary solution, since for $J~0$, $\dot{J}>$ 0. Assuming the momentum to be small, we linearize the last equation and find its solution: $\dot{J}=\epsilon r{\mathrm{\Omega }}^2\mathrm{\Delta }=-\epsilon r{\mathrm{\Omega }}^2\left|\mathrm{\Delta }\right|$, $J\left(t\right)=J_0-\epsilon r{\mathrm{\Omega }}^2\left|\mathrm{\Delta }\right|t,J_0-\epsilon$. Now we can estimate the time of the bounce $\left(t_b\right):t_{b1}=J_0\left(\epsilon r{\mathrm{\Omega }}^2\right|\mathrm{\Delta }|{)}^{-1}.$ In this case $J\to 0:\omega \left(J\right)\to \mathrm{\infty }$, $T\left(J\right)\to$ 0. Therefore, an infinite number of collisions must occur in time $t_{b1}$. R. Nagaev called such a dynamic phenomenon a quasiplastic impact [3]. This is a direct result of idealization, which arises from Newton’s hypothesis.

Consider secondly the case $R=$ 1; $\mathrm{\Delta }>$ 0, $B(p;x)=\text{2}bpx\equiv \text{2}b\dot{x}$, $b>$ 0. Using Eqs. (3), (5) after making some calculations (see also [5]) we obtain the equation:

We will estimate the time of the bounce. Let the initial impulse be small enough: $J_0-\sqrt{\epsilon }$. Then, estimating the function $E_1\left(J\right),$ we can show that $\epsilon E_1\left(J\right)=-\text{4}\epsilon {\mathrm{\Omega }}^2{\mathrm{\Delta }}^{2}b{J}^{-1}+{\epsilon }^2\dots$ and $J\left(t\right)=\sqrt{J_{{\mathrm{}}_0}^2-\text{8}\epsilon {\mathrm{\Omega }}^2{\mathrm{\Delta }}^{2}bt}$, $t_{b2}=J_{{\mathrm{}}_0}^2(\text{8}\epsilon {\mathrm{\Omega }}^2{\mathrm{\Delta }}^{2}b{)}^{-1}.$ In this case, when $\mathrm{\Delta }>$ 0, the period tends to a finite value for $J\to$ 0, so the number of collisions per time is finite.

The general analysis shows that for $\mathrm{\Delta }<$ 0, $b\ne$ 0, $R<$ 1, the bounce time is estimated with the help of $t_{b1}$, and for $\mathrm{\Delta }>$ 0, $b\ne$ 0, $R<$ 1 we use the estimate for the quantity $t_{b2}$. For systems with preload, we have a process with an infinite number of collisions (quasiplastic impact).

It can easily be shown that for $\mathrm{\Delta }=$ 0 both mechanisms of dissipation have the same effect on the process. The time for the termination of the regime with collisions is infinite.

Let's consider one more example. Let the energy losses occur due to the properties of the material. For example, the beams (springs) (Fig. 2) have a polymeric braid. Then:

where $\mathrm{\Gamma }\left(t\right)$ is the relaxation kernel [7], whose parameters are determined by the characteristics of the material of a beam with a polymer braid. The right side of the Eq. (6) ($r=$ 0) is:

We find that $\epsilon E_1\left(J\right)=-4\epsilon J{\omega }^3{\tilde{\mathrm{\Gamma }}}_s\left(\omega \right){\pi }^{-2}({\mathrm{\Omega }}^2-{\omega }^2{)}^{-2}$ ([5]), where ${\tilde{\mathrm{\Gamma }}}_s$ is the sine of the Fourier transformation of the relaxation kernel. The dissipative properties of the material are determined precisely by this quantity [7]. Further analysis depends on the specific type of relaxation nucleus. A detailed examination here is difficult. However, qualitative differences with the cases considered are small. The influence of material properties on the bounce should be considered only when carrying out high-precision calculations.

Thus, using the introduced change of variables, one can obtain a representation for the laws of variation of the relative and absolute coordinates:

where the function is determined with the help of the second relation Eq. (3) or in other.

Fig. 3 shows the laws of motion of colliding bodies and the times of rebound. For the case $\mathrm{\Delta }=$ 0, the decay time of the vibro-impact process is infinite, and the model needs to be refined. Fig. 3, $d$ shows the law of change in the relative coordinate. A similar graph will correspond to a body colliding with a fixed massive obstacle.

Fig. 3The laws of motion of colliding bodies

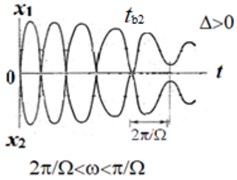
a)

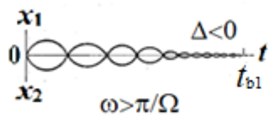
b)

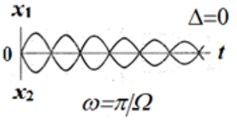
c)

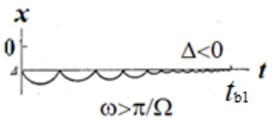
d)

5. Conclusions

The problems of analyzing the motions of systems with repeated damped collisions of elements are of engineering value, since they make it possible to estimate the parameters of the bounces accompanying these movements.

It is shown that the averaging technique in vibro-impact systems makes it possible to obtain important relationships for estimating the motion parameters of such systems. This is important for carrying out practical calculations.

It is shown that the character of the bounce modes in a special way depends on the models of energy dissipation and structural parameters.