Dynamic optimization mathematical model of the military subordinating interaction of two states

1. Introduction

In papers [1-3] and books [4-6] some general mathematical optimization model of a State was constructed by the author.

A progress to constructing on this base some general mathematical optimization model of interaction of several States came in 2018, when peaceful and military subordinating interactions of two States were mathematically formalized by the author [7]. Namely these kinds of interactions became the most noticeable events in the history of 20 and 21 centuries. The aim of either peaceful or military subordinating interactions is one and the same. It is the achievement of the largest divergence of joint wealth’s of interactive States up to the end of some time interval in favor of one of them. However, methods of control at these interactions may qualitatively differ from each other.

Further we consider only the military subordinating interaction by means of one-sided optimal control from the side of the aggressive State and in its favor. The paper is purely conceptual. Neither theoretical nor practical methods of solution of formulated optimization problems are considered in the paper. All customary terms are used in the mathematical sense only.

2. Organization and activity of a State

The mankind is the totality of all human beings lived or living on our planet. The united (i.e., material or mental) world (at the given time moment) is the totality including in itself: 1) the native world (material or mental) of the Earth and the Universe; 2) the over native world (material or mental) created by the mankind in the process of its being. The mankind itself is a part of over native world.

A society is some object of the united world including necessarily some part of mankind and all directly connected with its part of the over native world. A State (in the broad sense as State-Country) is a society, which structured into some complicated three level system with seven basic (sub)systems connected with each other in a single system and depending on each other so that the State cannot exist without any of them. The basic systems of the State are the existential, providing, accounting, joint administrative and supreme systems.

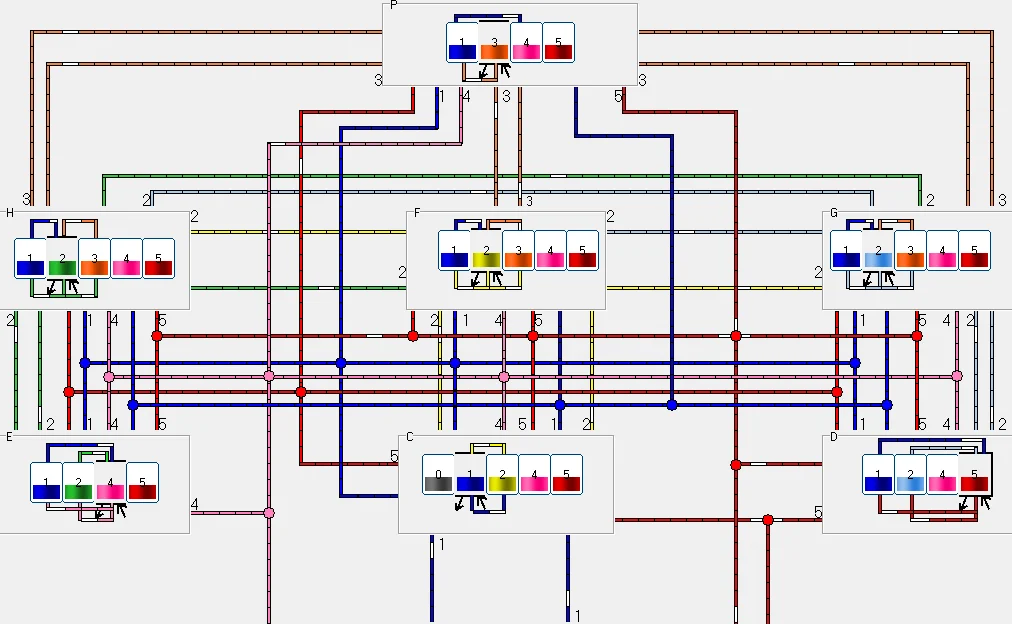
The existential system C realizes the metaagrarian (removing from the native environment), industrial (remaking), and servicing methods of vital activity. The providing system D provides the order, guarding, lawfulness, morality, and so on. The accounting system E realizes the production, collection, storage, and distribution of money, statistical date, and so on. The administrative systems F, G, and H rule over the existential, providing, and accounting systems, correspondingly. Therefore, they may be named by existential-administrative, providing-administrative, and accounting-administrative systems, correspondingly. They form the joint administrative system. The supreme (ruling) system P rules over the joint administrative system.

The State is an open system with three parts of the being surroundings named by the native surrounding (environment) $A_1$, the foreign over native surrounding $A_2$, and its own shady surrounding $A_3$. They are generally named the surroundings of the State.

Any mentally marked part of the State (including its population) and its internal environment will be called a wealth of the State. Wealths are contained in institutions of the State and in its surroundings. All these wealth are divided on the following kinds: existential (code 1), providing (code 4), accounting (code 5), administrative (code 2), and supreme (code 3). The unions of these wealths over all institutions of the basic system compose the wealths of the basic system of the given kind, and the unions over all basic systems of the State compose the wealths of the State of the given kind. The union of wealths of the State over all kinds of wealths composes the joint wealth of the State.

Every basic system produces the wealth of its own kind. Producing this wealth the system uses some of wealths existed in it. All basic systems are connected with each other by the streams of wealths. The existential, providing, and accounting systems get from the surroundings of the State and return to them the corresponding wealths.

3. General definition of wealths and streams of wealths of a State

Fix some State S. Consider the principal time interval $\left[T_1,T_2\right]$. On this interval we shall take a time moment t and a time increment $\mathrm{\Delta }t$ such that $T_1\le t-\mathrm{\Delta }t\le t\le t+\mathrm{\Delta }t\le T_2$. The totality of all concrete (over native) wealths of the kind m in the system $M$ at the moment t will be denoted by $V_M^m\left(t\right)$, and the totality of all concrete wealths of all kinds $m=$1, 2, 3, 4, 5 in all systems $M=$ C, D, E, F, G, H, P will be denoted by $V\left(t\right)$. Consider the complete totality $V(T_1,T_2)$ of all concrete wealths $x$, belonging to all totalities $V\left(t\right)$ for all t from the principal time interval $\left[T_1,T_2\right]$. Let $c\left(t\right)x$ denote the real value of the concrete wealth $x$ at the moment t evaluated in the money of the State S (see Section 4.6 from books [6, 7]). The number $W_M^m\left(t\right)$ equal to the sum of real values $c\left(t\right)x$ of all concrete wealths $x$ from the totality $V_M^m\left(t\right)$ will be called the evaluated joint wealth of the kind m of the system $M$ at the time moment $t$.

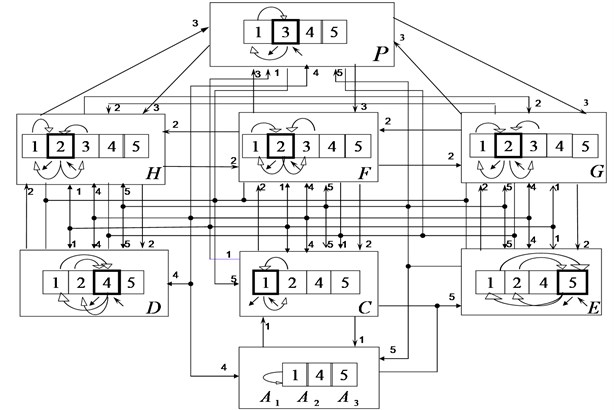
Fig. 1. The scheme of systems, wealths, and streams of the State

The totality $R_{MN}^{mn}(t-\mathrm{\Delta }t,t+\mathrm{\Delta }t)$ consisted of all concrete wealths $x$ from the complete totality $V(T_1,T_2)$, such that $x$ enters into the totality $V_M^m(t-\mathrm{\Delta }t)$, and $x$ does not enter into the totality $V_N^n(t-\mathrm{\Delta }t)$, and $x$ does not enter into the totality $V_M^m(t+\mathrm{\Delta }t)$, and $x$ enters into the totality $V_N^n(t+\mathrm{\Delta }t)$, will be called the stream on the time interval [$t-\mathrm{\Delta }t,t+\mathrm{\Delta }t$] from the totality of concrete wealths of the kind m of the system $M$ into the totality of concrete wealths of the kind n of the system $N$. The number $S_{MN}^{mn}(t-\mathrm{\Delta }t,t+\mathrm{\Delta }t)$, equal to the sum of real values $c\left(t\right)x$ of all concrete wealths $x$ from the stream $R_{MN}^{mn}(t-\mathrm{\Delta }t,t+\mathrm{\Delta }t)$, will be called the evaluated stream on the time interval [$t-\mathrm{\Delta }t,t+\mathrm{\Delta }t$] from the totality of concrete wealths of the kind m of the system $M$ into the totality of concrete wealths of the kind $n$ of the system $N$. The number $S_{MN}^{mn}\left(t\right)=\mathrm{l}\mathrm{i}\mathrm{m}\left(S_{MN}^{mn}\right(t-\mathrm{\Delta }t,t+\mathrm{\Delta }t)/2\mathrm{\Delta }t|\mathrm{\Delta }t\to 0)$ will be called the evaluated stream at the moment $t$ from the totality of concrete wealths of the kind m of the system $M$ into the totality of concrete wealths of the kind $n$ of the system $N$. Further the words “joint” and “evaluated” and the indication of time moment t we shall omit.

The representation of systems, wealths, and streams of the State S are given on Fig. 1.

4. The aggregate mathematical model of a State

The system of evolution equations of the State are composed according to the following preservation principle: the velocity of change of the valued joint wealth of some kind in some system at the time moment $t$ is equal to the sum of all entering valued streams of this wealth into this system at the time moment $t$ minus the sum of all outgoing valued streams of this wealth from this system at the time moment $t$. In the indicated above publications of the author the mathematical model of the State $S$ was described by means of the following system of equations of the State:

where $L_{EC}^{55}=a{W}_C^1(K-W_C^1)/(c+dr+(B_{E{C}_b}^{55}+B_{ED}^{55}+B_{EE}^{55}+B_{EF}^{55}+B_{EG}^{55}+B_{EH}^{55}+B_{EP}^{55}\left)\right)$, and:

where $K>$0, $a>$0, $c>$0, $d>$0, $0<e_i<1$, $0<p_i<1$ are some number parameters of the State $S$, $r$ is the key rate of the emission center of the State, $C_b$ is the budget subsystem of the existential system, and $B_{E{C}_b}^{55}$, $B_{ED}^{55}$, $B_{EE}^{55}$,$B_{EF}^{55}$, $B_{EG}^{55}$, $B_{EH}^{55}$, $B_{EP}^{55}$ are the budget streams from the accounting system into all the indicated systems of the State.

Consider the totality $\sigma [t_0,t]$ of all $S$-internal controls $r$, $B_{E{C}_b}^{55}$, $B_{ED}^{55}$, $B_{EE}^{55}$,$B_{EF}^{55}$, $B_{EG}^{55}$, $B_{EH}^{55}$, $B_{EP}^{55}$, assigned as functions of the time moment $t^{\text{'}}$ on the time interval $\left[t_0,t\right]$. The controls must be bounded both below and above by the following number inequalities: $r_0\le r\le r_1\text{,}$$(B_{DM}^{55}{)}_0\le B_{DM}^{55}\le (B_{DM}^{55}{)}_1$ for $M=C_b$, $D$, $E$, $F$, $G$, $H$, $P$.

The possible optimization task for the State $S$ is the following one. Consider the joint wealth $W_S(t,\sigma [t_0,t\left]\right)=(W_C^1+W_D^4+W_E^5+W_F^2+W_G^2+W_H^2+W_P^3)\left(t\right)$ of the State $S$ at the moment $t$ under the control $\sigma [t_0,t]$ on the time interval $\left[t_0,T\right]$. Consider the initial joint wealth $W_S\left(t_0\right)=(W_C^1+W_D^4+W_E^5+W_F^2+W_G^2+W_H^2+W_P^3)\left(t_0\right)$ of the State $S$ at the moment $t_0$. Take the possible objective function $\mathrm{\Phi }(t,\sigma [t_0,t\left]\right)=W_S(t,\sigma [t_0,t\left]\right)-W_S\left(t_0\right)$ of the increase of the joint wealth of the State $S$ at the moment t under the control $\sigma [t_0,t]$ relatively to its initial joint wealth at the moment $t_0$. The activity of the State S under some control ${\sigma }^{*}[t_0,T]$ is called optimal on the time interval $\left[t_0,T\right]$ with respect to the chosen objective function if for the activity of the State $S$ under any other control $\sigma [t_0,T]$ the following inequality $\mathrm{\Phi }(T,{\sigma }^{*}[t_0,T\left]\right)\ge \mathrm{\Phi }(T,\sigma [t_0,T\left]\right)$ is fulfilled. Formally it may be written in the form $\mathrm{\Phi }(T,\sigma [t_0,T\left]\right)\to max$ in the system of initial equations for the State $S$.

In papers [2, 3] some concrete-numerical play task on existence, finding, and approximate calculation of the optimizing controls was solved. The peculiarity of this task consists in the non-linearity of control occurrences into the equations. Nevertheless, the explicit optimal analytical solution of indicated system Eqs. (1-7) was found with the help of L. S. Pontryagin maximal principle at the following numerical dates: $T=$100, $K=$300, $d=$20, $a=$0.0005, $c=$1, $p_1=$0.3, $p_2=$0.6, $p_3=p_4=p_5=$0.2, $p_6=$0.7, $e_0=$0.015, $e_1=$0.005, $e_2=$0.02, $e_3=e_4=e_5=$ 0.005, $e_6=$0.01, $W_C^1\left(0\right)=$ 100, $W_D^4\left(0\right)=\text{20,}$$W_E^5\left(0\right)=\text{20,}$$W_F^2\left(0\right)=\text{10,}$$W_G^2\left(0\right)=\text{10,}$$W_H^2\left(0\right)=\text{10,}$$W_P^3\left(0\right)=\text{30,}$$r_0=$0.001, $r_1=$1, $(B_{EC{}_b{}^{\mathrm{}}}^{55}{)}_0=0\text{,}$$(B_{E{C}_b}^{55}{)}_1=$ 0.5, $(B_{DM}^{55}{)}_0=\text{0.1}$, $(B_{DM}^{55}{)}_1=\text{0.2}$, $M=$$D$, $E$, $F$, $G$, $H$, $P$.

The activity of S under the constant control $u^{*}\left(t\right)=r_0=$ 0.001, $v^{\mathrm{*}}\left(t\right)=(B_{E{C}_b}^{55}{)}_0=\text{0,}$$w_1^{\mathrm{*}}\left(t\right)=(B_{ED}^{55}{)}_1=\text{0.2}$, $w_2^{\mathrm{*}}\left(t\right)=(B_{EE}^{55}{)}_1=\text{0}\text{.}\text{2}$, $w_3^{\mathrm{*}}\left(t\right)=(B_{EF}^{55}{)}_1=\text{0.2}$, $w_4^{\mathrm{*}}\left(t\right)=(B_{EG}^{55}{)}_1=\text{0.2}$, $w_5^{\mathrm{*}}\left(t\right)=(B_{EH}^{55}{)}_1=\text{0}\text{.}\text{2}$, $w_6^{\mathrm{*}}\left(t\right)=(B_{EP}^{55}{)}_1=\text{0.2}$ for 0$\le t\le$100 proved to be optimal. Under this control the greatest value of the objective function $\mathrm{\Phi }(T,{\sigma }^{\mathrm{*}}[t_0,T\left]\right)$ of joint final wealth of the State at the time moment $T=$100 turned out to be 353,127. The greatest joint wealth of the State at the time moment $T=$100 is reached under the following controls: 1) under the lowest and constant key rate of the accounting system $r\left(t\right)=$0.001; 2) under the lowest and constant budget stream $B_{E{C}_b}^{55}\left(t\right)=0$ into the budget subsystem $C_b$ of the existential system; 3) under the highest and constant budget streams $B_{EM}^{55}\left(t\right)=\text{0.2}$ into the systems $M=D$, $E$, $F$, $G$, $H$, $P$. Under these controls both the wealth of the existential system and the joint wealth of the State are increase monotonically through $S$-figurative curve with the deceleration of velocity of increase.

5. Additional wealths and streams at the military interactions of two States

Further we shall consider two States: the State $S$ described above and some State $S\left(I\right)$, for which all the corresponding indications are furnished with the Roman digit $I$ in round brackets.

Compose some mathematical model of optimal concluding military subordination of the State $S$ to the State $S\left(I\right)$ at the condition of aggression of the State $S\left(I\right)$ upon the State $S$. For this purpose introduce into the existential system $C$ of the State $S$ some additional existential wealth 1($I$) of the system $C\left(I\right)$ of the State $S\left(I\right)$ and some additional providing wealth 4($I$) of the system $D\left(I\right)$ of the State $S\left(I\right)$. Introduce also the additional streams $Y_{D\left(I\right)C}^{4\left(I\right)4\left(I\right)}$, $Z_{CC}^{11\left(I\right)}$, $Z_{CC\left(I\right)}^{1\left(I\right)1\left(I\right)}$, $Z_{C\mapsto }^{11}$, and $Z_{C\mapsto }^{4\left(I\right)4\left(I\right)}$ for the system $C$, the name and sense of which are explained further. Besides, introduce into the providing system $D$ of the State $S$ some additional providing wealth 4($I$) of the system $D\left(I\right)$ of the State $S\left(I\right)$. Introduce also the additional streams $Y_{D\left(I\right)D}^{4\left(I\right)4\left(I\right)}$, $Z_{DD}^{44\left(I\right)}$, $Z_{DD\left(I\right)}^{4\left(I\right)4\left(I\right)}$, $Z_{D\mapsto }^{44}$, and $Z_{D\mapsto }^{4\left(I\right)4\left(I\right)}$ for the system $D$, the name and sense of which are explained further.

6. Names and senses of additional streams

The stream $Y_{D\left(I\right)C}^{4\left(I\right)4\left(I\right)}$ is called aggressive upon the system $C$ from the system $D\left(I\right)$ for the destruction and taking away indicated below. The stream $Z_{CC}^{11\left(I\right)}$ is called existentially pretaking away. It means that the existential wealth 1 of the system $C$ of the State $S$ is taking away by the State $S\left(I\right)$ by means of military “force” 4($I$), entering in the system $C$ in the form of the aggressive stream $Y_{D\left(I\right)C}^{4\left(I\right)4\left(I\right)}$, and is becoming the existential wealth 1($I$) of the system $C\left(I\right)$.

The stream $Z_{CC\left(I\right)}^{1\left(I\right)1\left(I\right)}$ is called existentially taking away. It means that the existential wealth 1($I$), taken away from the system $C$, is delivered into the system $C\left(I\right)$. The stream $Z_{C\mapsto }^{11}$ is called existentially destroying. It means that the existential wealth 1 of the system $C$ is destroying by means of the military “force” 4($I$), entering in the system $C$ in the form of the aggressive stream $Y_{D\left(I\right)C}^{4\left(I\right)4\left(I\right)}$.

The stream $Z_{C\mapsto }^{4\left(I\right)4\left(I\right)}$ is called expended with respect to the system $C$. It means that for the destruction of some part of the existential wealth 1 of the system $C$ and for taking away some other part of the wealth 1 from the system $C$ it is necessary to “sacrifice” with the military “force” 4($I$), getting out from the system $D\left(I\right)$ in the form of the aggressive stream $Y_{D\left(I\right)C}^{4\left(I\right)4\left(I\right)}$.

The stream $Y_{D\left(I\right)D}^{4\left(I\right)4\left(I\right)}$ is called aggressive upon the system $D$ from the system $D\left(I\right)$ for the destruction and taking away indicated below. The stream $Z_{DD}^{44\left(I\right)}$ is called providingly pretaking away. It means that the providing wealth 4 of the system $D$ of the State $S$ is taking away by the State S(I) by means of military “force” 4($I$), entering in the system $D$ in the form of the aggressive stream $Y_{D\left(I\right)D}^{4\left(I\right)4\left(I\right)}$, and is becoming the providing wealth 4($I$) of the system $D\left(I\right)$.

The stream $Z_{DD\left(I\right)}^{4\left(I\right)4\left(I\right)}$ is called providingly taking away. It means that the providing wealth 4($I$), taken away from the system $D$, is delivered into the system $D\left(I\right)$. The stream $Z_{D\mapsto }^{44}$ is called providingly destroying. It means that the providing wealth 4 of the system $D$ is destroying by means of the military “force” 4($I$), entering in the system $D$ in the form of the aggressive stream $Y_{D\left(I\right)D}^{4\left(I\right)4\left(I\right)}$.

The stream $Z_{D\mapsto }^{4\left(I\right)4\left(I\right)}$ is called expended with respect to the system $D$. It means that for the destruction of some part of the providing wealth 4 of the system $D$ and for taking away some other part of the wealth 4 from the system $D$ it is necessary to “sacrifice” with the military “force” 4($I$), getting out from the system $D\left(I\right)$ in the form of the aggressive stream $Y_{D\left(I\right)D}^{4\left(I\right)4\left(I\right)}$.

7. Connections between additional streams

Since some streams are evaluated in the money 5 of the State $S$, and others are evaluated in the money 5($I$) of the State $S\left(I\right)$, we are forced to express connections between streams, evaluated in different money, by means the conversion of these money into some fixed world currency $w$.

The number $s\left(t\right)$ from the equality $q\left(t\right)=s\left(t\right)q_w\left(t\right)$, where $q\left(t\right)$ is the quantity of the internal money 5 of the State $S$ and $q_w\left(t\right)$ is the quantity of the currency at the time moment $t$ of interchange of the internal money and the currency, is called the rate of exchange of the internal money 5 of the State $S$ onto the fixed world currency $w$ at the time moment $t$. Similarly, the number $s\left(I\right)\left(t\right)$ from the equality $q\left(I\right)\left(t\right)=s\left(I\right)\left(t\right)q_w\left(t\right)$, where $q\left(I\right)\left(t\right)$ is the quantity of the internal money 5($I$) of the State $S\left(I\right)$ and $q_w\left(t\right)$ is the quantity of the currency at the time moment $t$ of interchange of the internal money and the currency, is called the rate of exchange of the internal money 5($I$) of the State $S\left(I\right)$ onto the fixed world currency w at the time moment t.

Introduce four dimensionless real-valued positive functions of the current time $t$, varying in the time interval $\left[t_0,T\right]$.

The function $g^{\left(1\right)}$ will be called the index of effectiveness of destruction of the existential wealth 1 of the system $C$ by means of the military “force” 4($I$), getting out from the system $D\left(I\right)$ in the form of the aggressive stream $Y_{D\left(I\right)C}^{4\left(I\right)4\left(I\right)}$. The equality $(1/s)Z_{C\mapsto }^{11}=g^{\left(1\right)}(1/s(I\left)\right)Z_{C\mapsto }^{4\left(I\right)4\left(I\right)}$ shows the connection between the destroying stream $Z_{C\mapsto }^{11}$ in the system $C$ and the expended stream $Z_{C\mapsto }^{4\left(I\right)4\left(I\right)}$ in this system, evaluated through the fixed world currency $w$.

The function $h^{\left(1\right)}$ will be called the index of effectiveness of taking away the existential wealth 1 of the system $C$ by means of the military “force” 4($I$), getting out from the system $D\left(I\right)$ in the form of the aggressive stream $Y_{D\left(I\right)C}^{4\left(I\right)4\left(I\right)}$. The equality $(1/s)Z_{CC}^{11\left(I\right)}=h^{\left(1\right)}(1/s(I\left)\right)Z_{C\mapsto }^{4\left(I\right)4\left(I\right)}$ shows the connection between the pretaking away stream $Z_{CC}^{11\left(I\right)}$ in the system $C$ and the expended stream $Z_{C\mapsto }^{4\left(I\right)4\left(I\right)}$ in this system, evaluated through the fixed world currency $w$.

The function $g^{\left(4\right)}$ will be called the index of effectiveness of destruction of the providing wealth 4 of the system $D$ by means of the military “force” 4($I$), getting out from the system $D\left(I\right)$ in the form of the aggressive stream $Y_{D\left(I\right)D}^{4\left(I\right)4\left(I\right)}$. The equality $(1/s)Z_{D\mapsto }^{44}=g^{\left(4\right)}(1/s(I\left)\right)Z_{D\mapsto }^{4\left(I\right)4\left(I\right)}$ shows the connection between the destroying stream $Z_{D\mapsto }^{44}$ in the system $D$ and the expended stream $Z_{D\mapsto }^{4\left(I\right)4\left(I\right)}$ in this system, evaluated through the fixed world currency $w$.

The function $h^{\left(4\right)}$ will be called the index of effectiveness of taking away the providing wealth 4 of the system $D$ by means of the military “force” 4($I$), getting out from the system $D\left(I\right)$ in the form of the aggressive stream $Y_{D\left(I\right)D}^{4\left(I\right)4\left(I\right)}$. The equality $(1/s)Z_{DD}^{44\left(I\right)}=h^{\left(4\right)}(1/s(I\left)\right)Z_{D\mapsto }^{4\left(I\right)4\left(I\right)}$ shows the connection between the taking away stream $Z_{DD}^{44\left(I\right)}$ in the system $D$ and the expended stream $Z_{D\mapsto }^{4\left(I\right)4\left(I\right)}$ in this system, evaluated through the fixed world currency $w$.

8. Agreements about continuity of general streams

We shall assume that the transferred and transmitted streams are “equal” with respect to the world currency $w$, i.e., they are connected by the equalities $(1/s)Z_{CC}^{11\left(I\right)}=(1/s(I\left)\right)Z_{CC\left(I\right)}^{1\left(I\right)1\left(I\right)}$ and $(1/s)Z_{DD}^{44\left(I\right)}=(1/s(I\left)\right)Z_{DD\left(I\right)}^{4\left(I\right)4\left(I\right)}$.

According to the spoken earlier we assume that the expended stream $Z_{C\mapsto }^{4\left(I\right)4\left(I\right)}$ is equal to the aggressive stream $Y_{D\left(I\right)C}^{4\left(I\right)4\left(I\right)}$ (both of them are evaluated in the money 5($I$)), i.e., $Z_{C\mapsto }^{4\left(I\right)4\left(I\right)}=Y_{D\left(I\right)C}^{4\left(I\right)4\left(I\right)}$. Also according to the spoken earlier we assume that the expended stream $Z_{D\mapsto }^{4\left(I\right)4\left(I\right)}$ is equal to the aggressive stream $Y_{D\left(I\right)D}^{4\left(I\right)4\left(I\right)}$ (both of them are evaluated in the money 5($I$)), i.e., $Z_{D\mapsto }^{4\left(I\right)4\left(I\right)}=Y_{D\left(I\right)D}^{4\left(I\right)4\left(I\right)}$.

Using the indicated equalities we get the following correlations:

9. Changed and additional equations for State $\mathit{S}$

With respect to the additional streams Eqs. (1-7) for the State $S$ are transformed in the following ones:

where $L_{EC}^{55}=a{W}_C^1(K-W_C^1)/(c+dr+(B_{E{C}_b}^{55}+B_{ED}^{55}+B_{EE}^{55}+B_{EF}^{55}+B_{EG}^{55}+B_{EH}^{55}+B_{EP}^{55}\left)\right)$, and:

Note that the last negative summands in Eqs. (1) and (2) are appeared in virtue of the aggressive destruction and taking away.

For system of Eqs. (8-10) the previous initial totality $\sigma [t_0,t]$ of all $S$– internal controls $r$, $B_{E{C}_b}^{55}$, $B_{ED}^{55}$, $B_{EE}^{55}$, $B_{EF}^{55}$, $B_{EG}^{55}$, $B_{EH}^{55}$, $B_{EP}^{55}$, assigned as functions of the time moment $t^{\text{'}}$ on the time interval $\left[t_0,t\right]$, are considered.

10. Changed and additional equations for State $\mathit{S}\left(\mathit{I}\right)$

In the similar manner we get the following system of equations for the State $S\left(I\right)$:

where:

And:

Note that the last positive summands in Eqs. (1) and (2) are appeared in virtue of the adding by taking away.

For system of Eqs. (11)-(15) consider the initial totality $\sigma \left(I\right)[t_0,t]$ of all $S\left(I\right)$ – internal controls $r\left(I\right)$, $B_{E\left(I\right)C_b\left(I\right)}^{5\left(I\right)5\left(I\right)}$, $B_{E\left(I\right)D\left(I\right)}^{5\left(I\right)5\left(I\right)}$, $B_{E\left(I\right)E\left(I\right)}^{5\left(I\right)5\left(I\right)}$, $B_{E\left(I\right)F\left(I\right)}^{5\left(I\right)5\left(I\right)}$, $B_{E\left(I\right)G\left(I\right)}^{5\left(I\right)5\left(I\right)}$, $B_{E\left(I\right)H\left(I\right)}^{5\left(I\right)5\left(I\right)}$, $B_{E\left(I\right)P\left(I\right)}^{5\left(I\right)5\left(I\right)}$, assigned as functions of the time moment $t^{\text{'}}$ on the time interval $\left[t_0,t\right]$.

11. Mathematical model of the military subordinating interaction of two states

For system of Eqs. (11-15) consider the secondary totality $\tau \left(I\right)[t_0,t]$ of all $S\left(I\right)$-external controls $Y_{D\left(I\right)C}^{4\left(I\right)4\left(I\right)}$, $Y_{D\left(I\right)D}^{4\left(I\right)4\left(I\right)}$, $g^{\left(1\right)}$, $g^{\left(4\right)}$, $h^{\left(1\right)}$, $h^{\left(4\right)}$, consisting of all aggressive streams, indices of destruction, and indices of taking away. The joint control $\left(\sigma \right(I\left)\right[t_0,t],\tau (I\left)\right[t_0,t\left]\right)$ will be denoted by $u[t_0,t]$ and will be called the military (one-sided) joint control in system of Eqs. (11-15) for the State $S\left(I\right)$.

In the same manner as above consider the joint wealth $W_{S\left(I\right)}(t,u[t_0,t\left]\right)=\left(W_{C\left(I\right)}^{1\left(I\right)}+W_{D\left(I\right)}^{4\left(I\right)}+W_{E\left(I\right)}^{5\left(I\right)}+W_{F\left(I\right)}^{2\left(I\right)}+W_{G\left(I\right)}^{2\left(I\right)}+W_{H\left(I\right)}^{2\left(I\right)}+W_{P\left(I\right)}^{3\left(I\right)}\right)\left(t\right)$ of the State $S\left(I\right)$ at the time moment $t$ under the control $u[t_0,t]$ on the time interval $\left[t_0,T\right]$.

Consider the initial joint wealth $W_{S\left(I\right)}\left(t_0\right)=\left(W_{C\left(I\right)}^{1\left(I\right)}+W_{D\left(I\right)}^{4\left(I\right)}+W_{E\left(I\right)}^{5\left(I\right)}+W_{F\left(I\right)}^{2\left(I\right)}+W_{G\left(I\right)}^{2\left(I\right)}+W_{H\left(I\right)}^{2\left(I\right)}+W_{P\left(I\right)}^{3\left(I\right)}\right)\left(t_0\right)$ of the State $S\left(I\right)$ at the time moment $t_0$.

Take the objective function $\mathrm{\Psi }(t,u[t_0,t\left]\right)=W_{S\left(I\right)}(t,u[t_0,t\left]\right)-W_S\left(t_0\right)$ of the of the joint wealth of the State $S\left(I\right)$ at the moment $t$ under the military control $u[t_0,t]$ relatively to the initial joint wealth of the State $S$ at the moment $t_0$.

The interaction of the States $S$ and $S\left(I\right)$ under the military control $u[t_0,T]$ in system of Eqs. (11-15) for the State $S\left(I\right)$ will be called the military interaction and will be denoted by $A(S,S(I),u[t_0,T\left]\right)$. The military interaction $A(S,S(I),u[t_0,T\left]\right)$ will be called $\left(S\right(I),\alpha ,\beta )$ –subordinating (for the State $S$ with the numerical levels of subordinations $\alpha >\mathrm{}$1 and $\beta >\mathrm{}$1), if:

1) $W_{S\left(I\right)}(T,u[t_0,T\left]\right)-W_S\left(t_0\right)\ge \alpha \left(W_{S\left(I\right)}\right(t_0)-W_S(t_0\left)\right)$, i.e., $\mathrm{\Psi }(T,u[t_0,T\left]\right)\ge \alpha \mathrm{\Psi }\left(t_0\right)$ (the final divergence);

2) $W_{S\left(I\right)}(T,u[t_0,T\left]\right)\ge \beta W_{S\left(I\right)}\left(t_0\right)$ (the final enrichment).

Some military $\left(S\right(I),\alpha ,\beta )$-subordinating interaction $A(S,S(I),u^{\mathrm{*}}[t_0,T\left]\right)$ is called optimal on the time interval $\left[t_0,T\right]$ with respect to the chosen objective function $\mathrm{\Psi }(t,u[t_0,t\left]\right)$, if for any other military $\left(S\right(I),\alpha ,\beta )$ – subordinating interaction $A(S,S(I),u[t_0,T\left]\right)$ the following inequality $\mathrm{\Psi }(T,u^{\mathrm{*}}[t_0,T\left]\right)\ge \mathrm{\Psi }(T,u[t_0,T\left]\right)$ is fulfilled. Formally it may be written in the form $\mathrm{\Psi }(T,u[t_0,T\left]\right)\to max$ in system of Eqs. (11-15) for the State $S\left(I\right)$.