FEM simulation of the endlessly long fluid filled canal due to horizontal ground motion

1. Introduction

The dynamic behavior of fluid filling in moving containers is a phenomenon that has attracted the attention of geophysicists, engineers and mathematicians [1]. Liquid in an arbitrary shaped container under external excitations exerts the hydrodynamic pressure causing onto walls and bottom of fluid filled container together with hydrostatic pressure [2]. The knowledge of hydrodynamic effect of fluid on liquid storage tanks during the movement of the earth surface contributes to reliability and earthquake resistance of liquid-containing or liquid-transporting systems [11]. The design of containers loaded of earthquake is encouraged by various codes [3] IBC 2000, ACI codes, AWWA codes, API, Eurocode 8, NZSEE and Indian code. In this paper will be analyzed seismic response of rectangular infinitely long tank – canal by using of Eurocode 8 [4] and Indian standards [5] by simulating of Finite Element Method (FEM) with comparing of numerical solution using of FEM the Arbitrary-Lagrangian-Eulerian (ALE) formulation with the two way Fluid-Structure Interaction (FSI) techniques for simulation of the interaction between the structure and the fluid at the common boundary [6].

2. Seismic effect of fluid on channel

The solving of the Laplace equation for the motion of liquid contained in rigid channels can be stated as the two segregated contributions [7, 8]. They are called “impulsive”, and “convective”, respectively [9]. The “impulsive” component of the solution accepts the boundary conditions at the canal walls and the canal bottom but gives zero pressure at the original position of the fluid free surface in the static situation [10]. It is not correct, because the solution not taken the presence waves of the dynamic liquid response [11]. The second “convective”, called “sloshing” unaccepted the boundary conditions at the canal walls and the canal bottom, but gives the correct equilibrium condition at the free fluid domain surface [12].

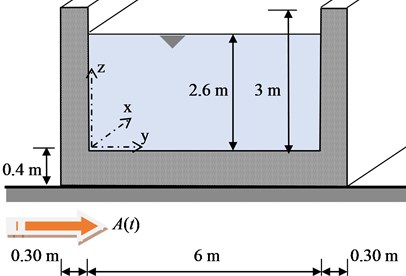
The considered a rectangular shallow founded infinitely long canal, having the width 2$L$, with uniform thickness walls [13]. Rectangular canal was filled with liquid to the height $H$. Thestorage structure is excited by a horizontal ground motion in the $y$ – direction, Fig. 1 [14].

The Laplace equation of rectangular channel whose walls can be considered as rigid that is excited by the horizontal ground motion can be given in the Eq. (1) [15]. The total hydrodynamic pressure is given as absolute summation of an impulsive and a convective contribution [16]:

The impulsive component can be expressed by:

where the function $q_i\left(z\right)$ [17] gives the variation of impulsive pressure in direction of the height, $L$ is the half of the channel width in the direction of the seismic loading, $\rho$ is mass fluid density. The time-history dependent ground acceleration $A_g\left(t\right)$ gives the time dependence of the pressure $p_i\left(z,t\right)$ in Eq. (2) [19].

The hydrodynamic convective pressure component can be obtained by the summation of modal sloshing terms, each one having a different variation in time [20]. The decisive contribution for rectangular channel is the first mode:

where $A_1\left(t\right)$ is the accelaration response function of a simple oscillator with frequency of the first fundamental mode with the appropriate value of damping, when is subjected to the input acceleration $A_g\left(t\right)$ [21]. The function $q_{c1}\left(z\right)$ [22] gives the distribution of impulsive pressure along the height for dominant first mode [23].

The first sloshing mode period of oscillation o is:

3. Numerical experiment and conclusion

The shallow founded reinforced concrete rectangular infinitely long fluid transporting canal is considered in presented numerical experiment, as seen in Fig. 1, without roof slab structure covered the channel.

The material characteristics of channel structure with Young’s modulus $E=$ 37 GPa, mass density $\rho =$ 2550 kg/m³ andPoisson ratio $\nu =$ 0.20. The mass density of fluid (H₂O) filling is ${\rho }_w=$ 1000 kg/m³.

Fig. 1The geometry of endlessly long canal

Response of open top liquid filled concrete canal was worked by using of FEMALE FSI formulation. This model was signed “Model FSI”. The solid walls and base of the canal was modelled by using 2D SOLID finite element with plain strain definition and the fluid inside the canal was modelled by using 2D FLUID finite elements under plain strain definition.

The alternative “quasistatic” approach of numerical simulation by using of FEM was considered by using of software ADINA too. In these approaches only solid domain of structure – the base and walls of the canal were modelled by plain strain definition of 2D SOLID finite element. The effect of fluid was simulated classically as the static loading by hydrostatic pressure together with hydrodynamic pressure.

The model “Model EC” use the hydrodynamic pressure distribution given by recommendation of Eurocode 8 [5]. The model “Model IS” use the hydrodynamic pressure distribution given by recommendation of Indian standards (IS) [6]. The horizontal ground motion given is given by the accelerogram of the earthquake Loma Prieta, California, 1989 [24]. The impulsive period $T_i=$ 0.041 s ($f_i=$ 24.52 Hz) and 5 % damped elastic response spectrum $S_a\left(f_i\right)=$ 1.87 m/s² is used for calculation of the effect of tank solid inertia and the hydrodynamic impulsive pressure. The first convective frequency $f_{c1}=$ 0.382 Hz and 0.5 % damped elastic response spectrum $S_a\left(f_{c1}\right)=$ 0.595 m/s² is used for calculation of hydrodynamic convective pressure.

The comparison of peak values of distribution of hydrodynamic impulsive pressure along the canal wall height by recommendation of EC8-4 and IS it is seen in Fig. 2(a). The Fig. 2(b) presents the comparison of peak values of distribution of hydrodynamic convective pressure along the tank wall height by recommendation of EC8-4 and IS.

The comparison of peak values of horizontal deformation of solid domain of canal, the peak Von Mises pressure in solid domain of channel and the peak fluid pressure for all three models were documented in Table 1.

Fig. 2a) The comparison of peak values of hydrodynamic impulsive pressure distribution along the canal wall height by recommendation of EC8-4 and IS, b) the comparison of peak values of hydrodynamic convective pressure distribution along the tank height by recommendation of EC8-4 and IS

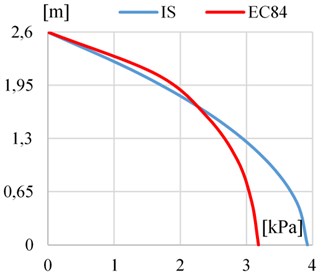
a)

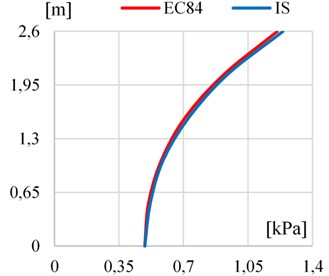
b)