Structural-acoustic modeling and analysis of an engineering machinery cab in the mid-frequency range

2.1. Theory of the hybrid FE-SEA method

In hybrid model, the FE part is represented by a set of degrees of freedom $q$, and the SEA subsystems by their average vibrational energy level $E$ [10-12]. The relation is written in terms of the cross-spectral matrix of force $S_{ff}$:

where $E\left[·\right]$ denotes the ensemble average, $D_{dir}$ is the “direct field” dynamic stiffness matrix, $\omega$ is the angular frequency and $n$ is the modal density of the SEA subsystem. The response of the FE dofs is given in cross-spectral form by:

where ${D_{dir}}^{\left(k\right)}\text{,}$$E_k\text{,}$ and $n_k$ represent “direct field” dynamic stiffness matrix, the average vibrational or sound energy level, and the modal density of the $k$th statistical subsystem. $S_{qq}$ and $S_{ff,d}$ represent the cross-spectral matrices of $q$ and $f$, and the dynamic stiffness matrix of the FE model $D_{tot}$ can be written as:

The average energy response of the SEA subsystems, written as:

where, power input $P_{(in,j)}^{ext}$ can be computed by the displacement response $q_d$ arising from external load $f$ applied to the subsystem $j$ and its dynamic stiffness matrix $D_{dir}^{\left(j\right)}$. ${\eta }_{ij}$ is the coupling loss factor.

Eq. (2) and Eq. (4) constitute primary equations of the hybrid FE-SEA method. Once, the energy response of SEA subsystem is computed by Eq. (4), the response of $q$ is also computed by Eq. (2) eventually.

2.2. Parameters of the hybrid model

For ideal subsystems, the modal densities of which can be given by Eq. (5) and Eq. (6):

where $N\left(f\right)$ is modes in band, $f$ is the representation of the frequency. $\omega$ is the circular frequency. $c$ is the sound speed. $V_0$ is the volume of the acoustic field. $A_s$ is the surface area of the acoustic cavity and $l_r$ is the total length of the edges.

DLF is a measure of the rate of energy flowing out of a subsystem through a dissipation mechanism, which is defined as follows:

where, structural loss factor (${\eta }_{ks}$) caused by internal friction of the $k$th subsystem is the inherent properties of materials. According to the structure loss factor-material table, ${\eta }_{ks}$ of tempered glass is 0.001 and ${\eta }_{ks}$ of steel plates range from 0.0001 to 0.0006. The loss factor of acoustic radiation (${\eta }_{kr}$) can be acquired from the Eqn. (8) and Eqn. (9):

where ${\rho }_0$ is the air mass density. $c$ represents the sound speed. ${\rho }_s$, $\delta$ represent the area density and radiation ratio of the structure. $A_p$ represents the radiation area. $P_r$ represents the circumference of the plate. $f_c$ represents the critical frequency. ${\lambda }_c$ represents the critical wavelength and $\beta$ represents the boundary condition factor. ($f_{c}t=$ 12.9 m/s with steel plate and $f_{c}t=$ 12.6 m/s with glass plate. $\beta =$ 1 with simple supported condition and $\beta =$ 2 with clamped condition).

The interior acoustic cavity regarded as semi-free sound field is written as:

where ${\eta }_c$ represents the loss factor of cavity. $\alpha$ represents the sound absorption coefficient, $A_s$ represents the surface area of cavity. $f$ is the center frequency, and $V$ represents the volume of cavity.

The coupling loss factors (CLFS) are created simultaneously when the appropriate wave fields are connected. As to the point connected subsystems, the CLFs can be acquired by the Eq. (11):

where$\mathrm{}{Z}_i+Z_j$ is the total impedance of the point junction. $n_i\left(\omega \right)$ is the model density of subsystem $i$ and $R_i$, $R_j$ is the real part of input impedance at the point junction between subsystems $i$, $j$, respectively.

The CLFs for the line junction subsystems can be defined as:

where $l$ represents the length of coupling line, $c_g$ is the bending wave velocity of subsystem, $A_i$ represents the surface area, and ${\tau }_{ij}$ is the wave transmission coefficient from subsystem $i$ to $j$.

For the area coupling structure, the CLFs can be defined as follows:

where ${\eta }_{sc}$, ${\eta }_{cs}$ represents the DLF from structural subsystem to acoustic cavity and the reverse one, respectively. ${\sigma }_{sc}$ represents the sound radiation coefficient from structural subsystem to acoustic cavity.

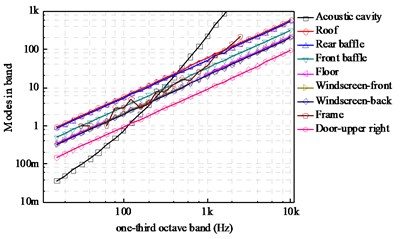
Fig. 1a) Structural-acoustic system of engineering machinery cab, b) modes per 1/3rd octave band for the principal structural subsystems

a)

b)

3.1. Description of the structural-acoustic system

In this paper, we are interested in studying the acoustic response of an engineering machinery cab at passengers’ ears under engine’s structure-borne and air-borne excitations in middle frequency range. The cab is made of two shield panels, two windscreen panels, four door glass panels and two top and bottom panels, plotted in Fig. 1(a). The frame is of rectangular shape and made of connected steel beams with different cross sections. The cavity encloses a volume of $V_0=$ 2.63 m³ and the total surface area is $A_s=$ 13.48 m².

3.2. Modeling of the cab based on the hybrid model

In this study, most of subsystems in the cab are simplified into regularly ideal flat plates, singly-curved shells etc. The modal densities of subsystems are estimated based on analytical methods above shown in the Fig. 1(b). According to the mid-frequency domain division principle [9], the hybrid model can be used from 100 Hz to 800 Hz.

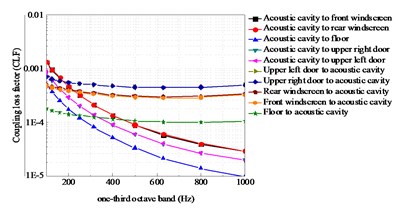
DLFs of the major subsystems were shown in Fig. 2 and CLFs for each junction calculated by analytical equations were shown in Fig. 3. As can be observed, the coupling loss factors of acoustic cavity to rear windscreen does not equal to the reverse one. This indicates the directionality of coupling loss factors.

Fig. 2DLFs for the principal structural subsystems

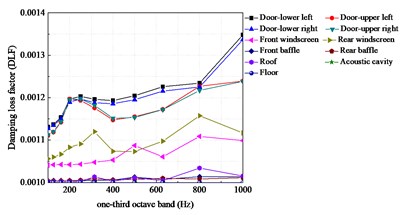
Fig. 3CLFs between the front windscreen and the acoustic cavity

3.3. Excitations of the hybrid cab model

The cab mounting system is supported with four symmetric mounts: left front mount (L-F), right front mount (R-F), left rear mount (L-R) and right rear mount (R-R). Four accelerometers were placed in the passive sides of cab mounting system and accelerations of these were collected at the highest speed in static situation. Meanwhile, the sound radiation excitations were measured by surface acoustic sensors in same condition.

Then excitation forces can be figured out by imposing integral transform on acceleration signals. The forces were defined as follows:

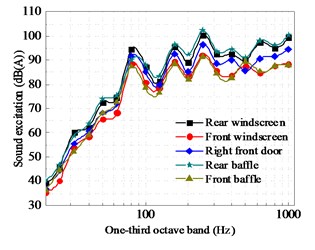
where $\ddot{x}{\left(f\right)}_{active}$ and $\ddot{x}{\left(f\right)}_{passive}$ represent the acceleration at mounting system of the cab and the vehicle body, $K_i$ represents the stiffness of the mount. The vibration and sound radiation excitations of the cab respectively was plotted in Fig. 4 and Fig. 5.

Fig. 4Vibration excitations for the mounting system

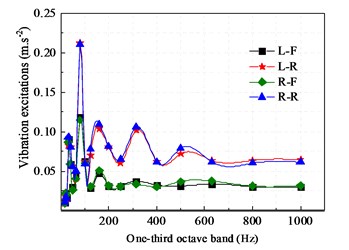
Fig. 5Sound excitations of the primary panels

3.4. Results analysis

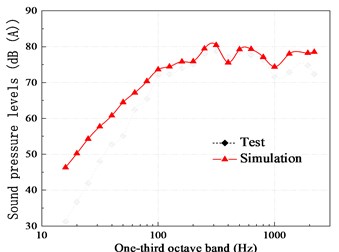
The results by averaging the sound responses through experiment in the engineering machinery cab is compared with that of the hybrid FE-SEA method plotted in Fig. 6. It is shown that in general the predicted results are in good agreement with the test results. The frequencies at the peaks and variation trend in the response are basically consistent from 100 Hz to 800 Hz. Some discrepancies were also observed at lower frequencies due to low modal density shown in Fig. 3 which does not meet the application assumptions of SEA in this band. Moreover, another possible reason could be the assumption of hard-wall boundary conditions, whereas the actual cab has tiny holes and gaps because of doors, windows and pipelines.

Fig. 6Comparisons (SPLs) between the predicted and test results