Research on the transmission loss of the floor aluminum profile for the high-speed train based on FE-SEA hybrid method

2.1. Reciprocal relation of subsystems

The system will be divided into many meshes when the dynamic response of system is analyzed by the finite element method. Each node will generate the corresponding displacement in the various degrees of freedom. On the boundary, the displacement $q$ in the boundary degree of freedom can be expressed as follows [11]:

where $f$ is the external excitation, and $D$ is the stiffness matrix.

Elastic waves generated by the boundary harmonic vibrations are propagated through system to the boundary region for reflection. In the dynamic stiffness matrix $D$, the part without reflection is defined as the direct dynamic stiffness matrix $D_{dir}$, and there is a difference of “reverberation” force $f_{rev}$ between the boundary force $D_{dir}q$ and the actual boundary force $Dq$ as follows:

Eq. (2) is then substituted into Eq. (1) to obtain the following formula [20]:

where, the subscripting “$rev$” means “reverberation”, and “$dir$” represents direction.

Based on wave propagation theory, the following formula can be obtained if the sound field is the diffusion field:

where, $E\left[\right]$ is the mean value of all structures, and $E$ is the vibration energy of the plate subsystem. $n$ is the modal density of the subsystem. The superscripting $T$ indicates the matrix transpose, and $Im$ represents the imaginary part. Therefore, Eq. (4) is the reciprocity relation of the diffusion field.

2.2. Hybrid FE-SEA system function

The coupling effect between FE subsystem and SEA subsystem can be expressed by Eq. (4). The response of the deterministic system can be expressed as follows:

where, $D_d$ is the dynamic stiffness matrix of FEM subsystem, and $S_{ff}$ indicates the mutual spectral of excitation force applied to FEM subsystem. $D_{dir}^{\left(k\right)}$ means the average dynamic stiffness matrix of the subsystem$k$. $E_k$ is the vibrational energy of the subsystem $k$. $n_k$ is the modal density of the subsystem $k$. $\omega$ is the angular frequency. The subscripting $qq$ represents the deterministic system, and the subscripting $ff$ indicates the mutual spectra. The subscripting $k$ and superscript $\left(k\right)$ means $k$th subsystem. The subscripting $d$ means the dynamic stiffness, and the subscripting $t$ means the total dynamic stiffness. Since the power of each subsystem is balanced, the power balance equation of FE-SEA coupling system is as follows [12]:

where ${\eta }_j$ is the damping loss factor of the subsystem $j$, and $P_j$ is the input power of the subsystem $j$. $P_{m,j}$ is the input power generated from the force which is applied on the deterministic system. ${\eta }_{jk}$ is the coupling loss factor of subsystem $j$ and $k$. The subscripting $j$ and $k$ represent the $j$th and $k$th subsystem, respectively. According to Eq. (7), the energy response of the system can be obtained, and the responseof the deterministic system can also be obtained from Eq. (5).

3.1. Sound pressure method

where ${\stackrel{-}{L}}_{P_i}$ is the average value of sound pressure level in the incidence side. ${\stackrel{-}{L}}_{P_o}$ is the average value of sound pressure level in the transmission side. $S$ is the surface area of the wooden component. $A$ is sound absorption. $V$ is volume of reverberation chamber. $T$ is reverberation time. The detailed experiment process can refer to reference [21].

3.2. Sound intensity method

The computational formula for sound intensity is as follows. $I_o$ is the transmission intensity, $\rho$ is density, and $c$ is sound speed in air. The other parameters have been described in the above:

Fig. 1Experimental process of transmission loss

a) The incidence side

b) The transmission side

Fig. 2Comparison of experimental result for two methods under 1/3 octave

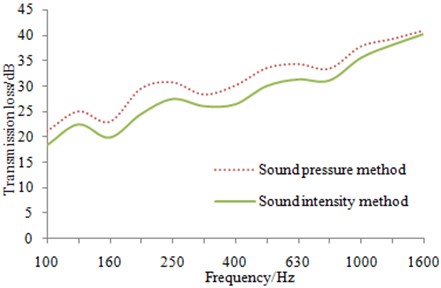
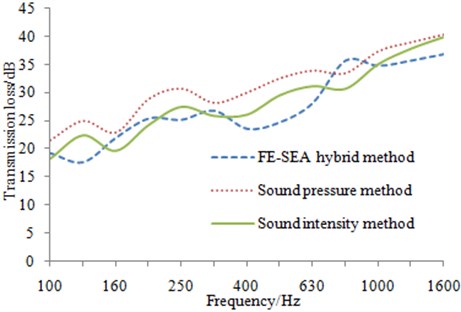
As shown from Fig. 2, the transmission loss of the aluminum profile is obtained by the sound pressure and sound intensity methods. It can be found that two curves have shown the consistent trends, while the transmission loss is differed about 3 dB at middle and low-frequency band below 1000 Hz, which may be related to the installation state of the experimental plate. As hooks are existed at both ends of the aluminum profile structure, the sealing of the aluminum profile and installation is hard to be made. Under the actual installation conditions, there may be sound leakage which affects less on far-field sound pressure but larger on near-field sound intensity. As a result, the radiation sound power is large and the transmission loss is small. Therefore, transmission loss obtained by sound intensity method would be lower than that obtained by sound pressure method in middle and low-frequency band. In addition, the transmission loss of the aluminum profile has shown a steady upward trend. Moreover, transmission loss at the frequency below 800 Hz is slowly increased, while that at the frequency over 800 Hz is rapidly improved. Therefore the coincidence frequency of transmission loss for the aluminum profile is about 800 Hz.

4.1. The finite element model of the aluminum profile

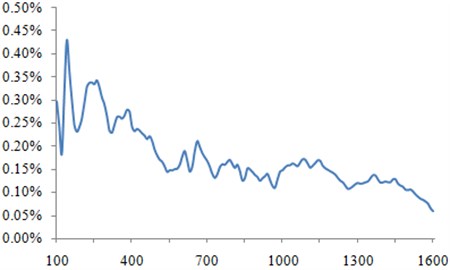
Damping loss factor is an important parameter for the finite element model. As a result, it should be measured. In this paper, it is measured as shown in Fig. 3 according to the method proposed by reference [21].

Fig. 3Damping loss factor of the aluminum profile

As shown in Fig. 4, the aluminum profile is a special structure which is made of two aluminum plates connected by sound-bridge. Considering the important impact of sound bridge on the vibration energy, some geometric characteristics will be missed due to building two-dimensional model. As a result, the computational model of the aluminum profile is built by using three-dimensional, as shown in Fig. 5. The structural and material parameters are shown in Table 1.

Fig. 4Geometric characteristics of the aluminum profile

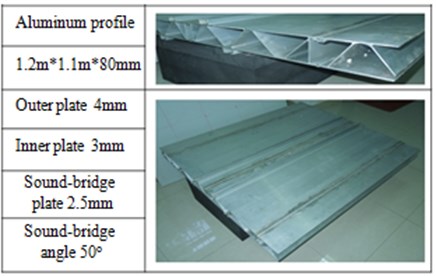
Fig. 5Three-dimensional model of aluminum profile

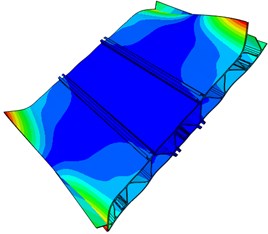
In order to verify the accuracy of the finite element model, the free modal test is conducted on the aluminum profile. Multi-points excitation and single-point response are adopted in the test. The aluminum profile is hung with a flexible rope, and the collection points are arranged in the positions with greater structure response. Besides, each excitation point is hammered three times. Frequency response functions with better consistency are selected. Finally, all frequency response functions are conducted on modal fitting to obtain modal parameters of the aluminum profile. The simulation and experimental results of free models are compared to verify the reliability of the finite element model, whose models are shown in Fig. 6.

As seen in Fig. 6, the first order modal refers to the torsional vibration. The second and third order modals are the bending vibration. The fourth and fifth order modals mainly show the torsional vibration at both ends, and the sixth order modal is the composite vibration. Among them, the positions with maximum amplitude are concentrated on both ends of the plate, because the aluminum profile is cut according to the experimental requirements and sound-bridge on both ends is not connected with the upper surface. As a result, the structure is weak in the both ends and easily generates the local vibration.

Fig. 6Modal shape of the first six orders for the aluminum profile

a) First order

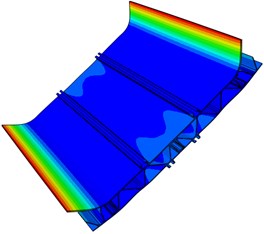
b) Second order

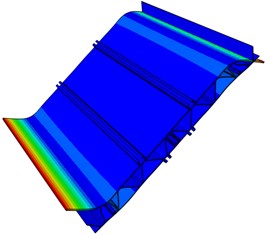
c) Third order

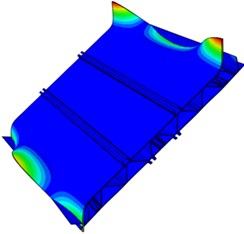
d) Fourth order

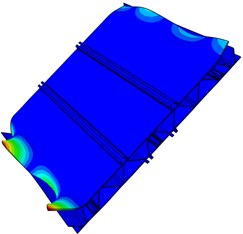
e) Fifth order

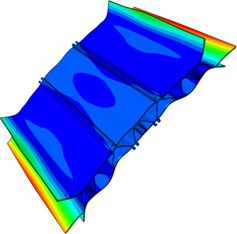
f) Sixth order

4.2. Selection of computational method and verification of transmission loss

The structural-acoustic coupling method is also applied in the paper to calculate the transmission loss of the aluminum profile, whose simulation model is shown in Fig. 7. It can be seen that meshes of three-dimensional sound cavity are established on both sides of the finite element model of the aluminum profile in order to simulate the sender chamber and receiving chamber respectively. As known by Principle of 1/6 Wavelength, the maximum length of sound cavity element is 28 mm, which satisfies the calculation accuracy within 2000 Hz. In the process, all outer surfaces of the sound cavity are endowed with the attributes of self-adaptive matching layer in order to completely absorb and radiate sound power. And the structural meshes of both the inner surface and aluminum profile are defined as the structure-acoustic coupling surfaces to transfer the acoustic energy. The original boundary conditions applied by the simulation are simply-supported constraints for four longitudinal edges along the sound bridge, as well as the excitation source of 1 Pa reverberant sound at the incident side. Finally, the calculation results are compared with the experimental result, as shown in Fig. 8. It can be seen that better consistency can be found in the low frequency within 400 Hz while unreliable simulation result is appeared in the frequency range of more than 400 Hz. Such result can be explained by the complex structure of the aluminum profile that has many sound bridge structures rather than a regular panel. Therefore, the structural modal would be very intensive when the analyzed frequency is more than 400 Hz, thus resulting in serious errors by means of FEM techniques at this time.

Based on the mentioned analysis, FE-SEA hybrid method is also applied in the paper to compute the transmission loss of the aluminum profile, as shown in Fig. 9. The upper and lower panels, sound bridges and other substructures of the aluminum profile are firstly divided into different mesh sets in the finite element software HYPERMESH, and then applied appropriate constraints. Later, the finite element model is imported into VAONE, and different mesh sets are selected to generate the corresponding subsystems. In the generation of the finite element subsystem, meanwhile, FE Face can be generated automatically from the software. At the incident side, 1 Pa reverberant sound source is applied on the FE Face in order to simulate the noise source in the experiment. In addition, semi-wireless fluid fields which are equivalent to SEA subsystem are defined at the incident side and transmission side respectively, in order to collect the radiation sound energy of the aluminum profile structure. After obtaining FE-SEA hybrid model of the aluminum profile, the transmission loss at the 1/3 octave band is computed in the software directly, as shown in Fig. 10. As can be seen Fig. 10, better consistency is found between the simulation and experimental results, thus indicating that the calculation method is obviously better than the traditional structural-acoustic coupling method.

Fig. 7Structural-acoustic coupling model of the aluminum profile

Fig. 8Simulation and experimental comparison of transmission loss

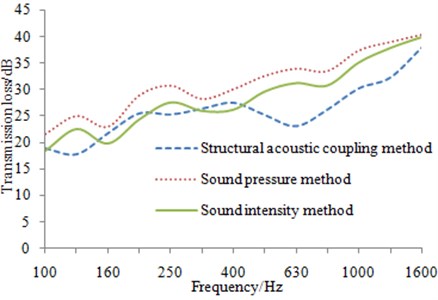
In addition, it can be seen at the middle and low-frequency between 100 Hz-1600 Hz, the simulation and experimental results are basically same in the change trend. For the experimental value, three insulation troughs which are 160 Hz, 315 Hz and 800 Hz are presented. However, the second insulation trough of the numerical results is at 400 Hz, this is caused by the differences in boundary conditions. In addition, the transmission loss obtained by sound pressure method is always higher than that of sound intensity method, and the difference is about 2.5 dB. Transmission loss curve obtained by the simulation is more close to the result of sound intensity method at the frequency band below 315 Hz, and more close to the result of sound pressure method at the frequency band over 630 Hz. Therefore, FE-SEA hybrid method is reliable to be predicted the transmission loss of the aluminum profile at the middle and low-frequency.

Fig. 9FE-SEA hybrid model of the aluminum profile

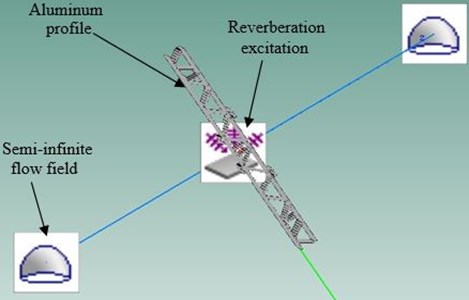
Fig. 10Simulation and experimental comparison of transmission loss

5.1. Structural design

The aluminum profile of the high-speed train is comprised of the upper and lower panels as well as the middle sound bridge. Since the upper and lower panels are the regularly planar structure, the geometric design towards them is of no significance. Therefore, the structural design of the aluminum profile is mainly reflected in the design of sound bridge. Currently, the sound-bridge forms of the aluminum profile are mainly divided into triangular, trapezoidal and quadrilateral.

The overall height of the aluminum profile and the thickness of each plate are remained constantly. Then the trapezoidal structure is attempted to change into quadrilateral and triangular structure as shown in Fig. 12, and the corresponding transmission loss is also calculated, whose results are shown in Fig. 13.

Fig. 12Cross sections of the aluminum profile with two kinds of sound bridges

a) Cross section of the aluminum profile with quadrangular sound bridge

b) Cross section of the aluminum profile with triangular sound bridge

Fig. 13Comparison of transmission losses for the aluminum profile with two kinds of sound bridges

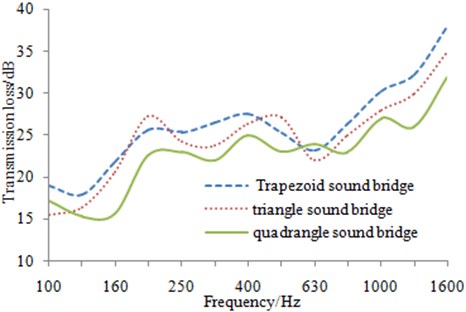
Triangular and trapezoidal sound bridges are of little difference as can be seen from Fig. 11 and Fig. 12. The trapezoidal structure is only featured with a smooth transitional cycle on the top, similar to the triangular structure. However, the external excitation can be better attenuated by such transitional cycle in the actual project, and the transmission loss reflected by the trapezoidal structure can be found in Fig. 13. The transmission loss of the aluminum profile with the trapezoidal sound bridge is higher than that of the triangular structure in most frequency points, except 200 Hz and 500 Hz where the transmission loss of the aluminum profile with the triangular sound bridge is increased by 2.3 dB and 2.1 dB respectively when it is compared to the original structure. It can be possibly explained by the modal changes at these frequency points caused by the minor structural changes. The average transmission losses of both trapezoidal andtriangular sound bridges are 26.1 dB and 24.7 dB, respectively, thus further indicating the better sound insulation effect of trapezoidal sound bridge. In addition, relatively small amplitude of the transmission loss and relatively concentrated modal density can be found in the entire frequency band for the aluminum profile with quadrilateral sound bridge. It is mainly because quadrilateral structure has poorer stability and relatively concentrated modal density than the triangular structure, thus reflecting more peaks and valleys in terms of the transmission loss curve. The average transmission loss of the quadrilateral bridge is 22.8 dB, significantly smaller than the mentioned two structures. In combination with the above analysis, it can be found the reasonability of trapezoidal sound bridge applied in the aluminum profile structure of the high-speed train.

5.2. Sound-bridge angle

The original section characteristics of the aluminum profile are shown as Fig. 11. Sound-bridge angle is 35° and it has 8 sound-bridges. The thickness of each plate remains unchanged, sound-bridge angle is increased to 60° with 5° as the step length, and two-dimensional model of the aluminum profiles is built, and the basic parameters are shown as Table 2.

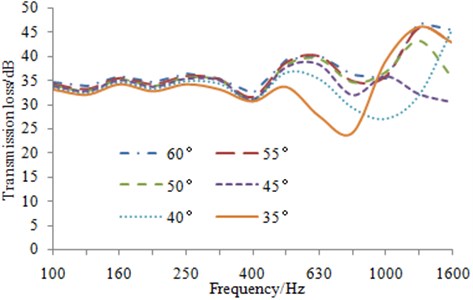
Similarly, FE-SEA hybrid method is applied to compute sound insulation performance of the aluminum profile under free boundary conditions, whose result is shown in Fig. 14. First of all, it is shown from Table 2 that although sound-bridge angle of the aluminum profile is increasing, the first order torsion and bending frequency has shown little change under free boundary condition. Therefore, it is reflected that the result of 1/3 octave spectrum has illustrated sound insulation trough concentrated at 400 Hz, as shown in Fig. 14. Before the first order torsional frequency, the transmission loss is quite gentle, and acoustic waves in the vertical section are equivalent to that passing through three layers of the aluminum plate. Therefore, the transmission loss is proportional to the number of sound-bridge. After 400 Hz, the transmission loss is more affected by mass law and structure resonance. With the increase of sound-bridge angle, especially after 50°, the modals number of the aluminum profile is significantly reduced. Transmission loss frequency is in conformity to mass law in all spectrums except the trough of modal frequencies. As can be seen in Fig. 14, the transmission loss is improved along with the increase of sound-bridge angle. Generally speaking, the aluminum profile at 55°-60° can be chosen for regions with higher structural strength, and transmission loss can be ensured at better level. However, the aluminum profile at 35°-40° can be selected when structural lightweight is the important index. Though the sound insulation performance of the structure itself is sacrificed, sound package can be applied for improving the sound insulation performance.

Fig. 14Transmission loss curve of the aluminum profile under different sound-bridge angles

5.3. Plate thickness

Based on the above analysis, 55° is chosen as sound-bridge angle. The basic geometric dimension is remained the same, the thickness of inner plate, sound-bridge plate and outer plate is chosen as variable, and structure-acoustic coupling method is applied to study the acoustic performance of the aluminum profile under the free boundary constraint.

Fig. 15Transmission loss with different plate thicknesses

a) Transmission loss with inner panel thickness

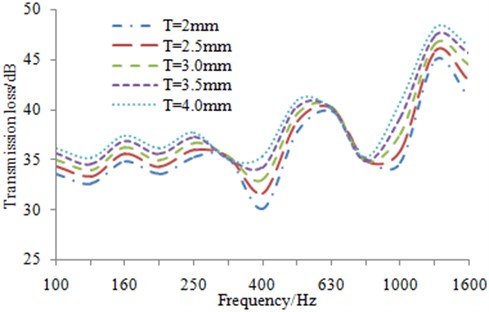
b) Transmission loss with sound-bridge plate thickness

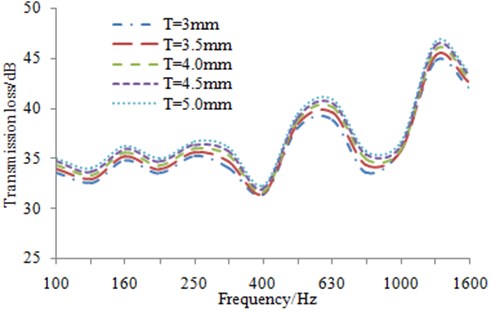
c) Transmission loss with outer plate thickness

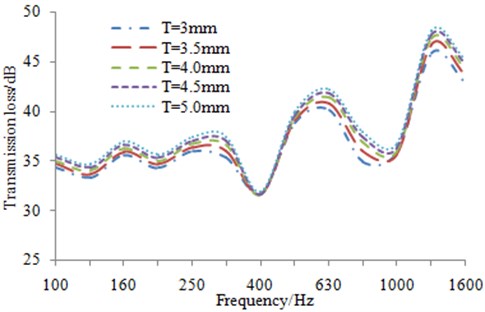
Since the lightweight of the high-speed train is affected by the plate thickness directly, the allowed change scope is very limited. Considering that the combination of 3 mm outer plate, 2.5 mm sound-bridge plate and 4 mm inner plate is mostly applied in the structure of the original high-speed train, the thickness range of outer plate, sound-bridge plate and inner plate is defined as 3 mm-5 mm, 2 mm-4 mm and 3 mm-5 mm, respectively, and the corresponding step length is 0.5 mm. The simulation result of the transmission loss is shown in Fig. 15. As shown from Fig. 15, it is indicated that after increasing thickness for inner and outer plate of the aluminum profile, modals frequency and transmission loss trough have a little change. But structural mass and surface density are increased meanwhile, therefore transmission loss at other frequency bands is improved. And the maximum optimization value at the central frequency band of a single one-third octave band is about 3 dB. Therefore, on the premise of requirements for the structural strength and lightweight indexes of the aluminum profile, the appropriate thickening treatment is conducted for sound-bridge plate, which is a reasonable solution to optimize the sound insulation performance of the aluminum profile.

5.4. Structural material

Steel, aluminum and magnesium are three kinds of commonly-used structural materials. Initially, trains used high-strength steel and stainless steel as the body structure. Afterwards, the aluminum alloy became the preferred material of high-speed trains due to its advantages such as small proportion and high strength. As a kind of new lightweight material, magnesium alloy is applied in the field of aerospace and automobile in the past. This paper takes the same structure as the research object and compares the advantages and disadvantages in terms of vibration and acoustic performance by means of replacing materials. The basic material parameters are shown in Table 3.

Fig. 16Transmission loss curves of the structure with three kinds of materials

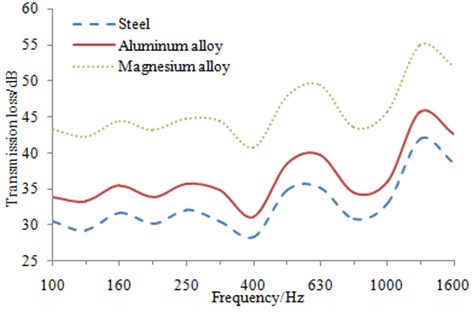
The simulation result of the transmission loss is shown in Fig. 16, which shows that the structures with different materials present obvious differences under the same volume. Steel has maximum bulk density and also the best sound insulation performance under the influence of mass law. The second is the aluminum alloy whose transmission loss is about 9 dB less than that of steel. Magnesium alloy will be the last one, due to its minimum bulk density and mass. Magnesium alloy is around 3.5 dB less than aluminum alloy in terms of transmission loss. The free modal frequencies of three kinds of materials do not differ much. Therefore, the sound insulation trough also stays the same basically. In the practical engineering, the bulk density of steel is about three times that of the aluminum alloy and it is very difficult to satisfy the demand of high-speed trains for lightweight. Magnesium alloy is only 2/3 the bulk density of that of aluminum alloy, but its panel needs to be thickened in order to reach the same transmission loss. In addition, magnesium alloy is usually used in the structural parts without high demand for impact resistance as its structural hardness is still flawed. Therefore, the structure which is designed by adopting aluminum alloy materials is the most reasonable main structure of high-speed trains.