Uncertain optimization of in-bore launching performance of artillery based on interval method

Xu, Fengjie; Yang, Guolai

doi:10.21595/vp.2019.21030

Vibroengineering Procedia

Browse Procedia

Published: 19 October 2019

Check for updates

Uncertain optimization of in-bore launching performance of artillery based on interval method

Fengjie Xu¹

Guolai Yang²

^{1, 2}School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing, China

Corresponding Author:

Guolai Yang

Cite the article Download PDF

Downloads 1398

CrossRef Citations 1

Abstract

In order to study the uncertainty optimization of the in-bore launching performance of larger-caliber artillery, the interior ballistic program was compiled and embedded in ABAQUS finite element software for secondary development, and the dynamic model of in-bore launching was built. The structural parameters of bore, the structural parameters of projectile and parameters of launching propellant were considered, and the uncertainty was described by interval number. BP neural network was used to construct a surrogate model for the dynamic model of in-bore launching. The deterministic transformation of uncertain objective function and uncertain constraints was carried out by using interval order model and interval probability model respectively. The interval uncertainty optimization model of the in-bore launching performance artillery was established by taking the interval radius and midpoint of the projectile muzzle velocity as objective functions and the maximum chamber pressure as constraint. Multi-objective genetic algorithm was used to solve the problem, and the optimal solution and reasonable interval of uncertain parameters were obtained.

Uncertain optimization of in-bore launching performance of artillery based on interval method

Highlights

The analysis model of artillery in-bore launching performance is established
The interval method is applied to the uncertain optimization of artillery system
Finite element model and internal ballistic subroutine

1. Introduction

The in-bore launching performance is the key performance of artillery. The motion of projectile in the chamber is affected by many uncertain factors which is the fundamental reason of the difference of ballistic performance. These uncertain factors include: the structural parameters of the gun barrel, the structural parameters of the projectile and parameters of launching propellant.

At present to research in the field of artillery systems rarely involve uncertainty optimization research. Most research focuses on artillery firing dynamics. The research of artillery optimization rarely involves parameter uncertainty. Wang Liqun [1] used the stochastic robust design theory to optimize the firing density, but the research neglected the stage of projectile motion in the chamber. The design variable optimization results obtained by deterministic optimization of the in-bore launching performance are all deterministic parameter combinations, which are not suitable for solving the uncertain problems in actual production. Therefore, this paper, from the point of view of the integrated design of projectile, gun and propellant, carried out the uncertain optimization of the in-bore launching performance. Firstly, the interior ballistic model and finite model element model were combined to construct the gun in-bore firing dynamics model. Then, based on the interval uncertainty optimization theory, the uncertain optimization model of gun bore firing performance is constructed, and the parameter interval of uncertain design variables is obtained by combining BP neural network surrogate model technology and multi-objective genetic algorithm for optimization solution.

2. Artillery in-bore launching model

2.1. Finite element mesh model

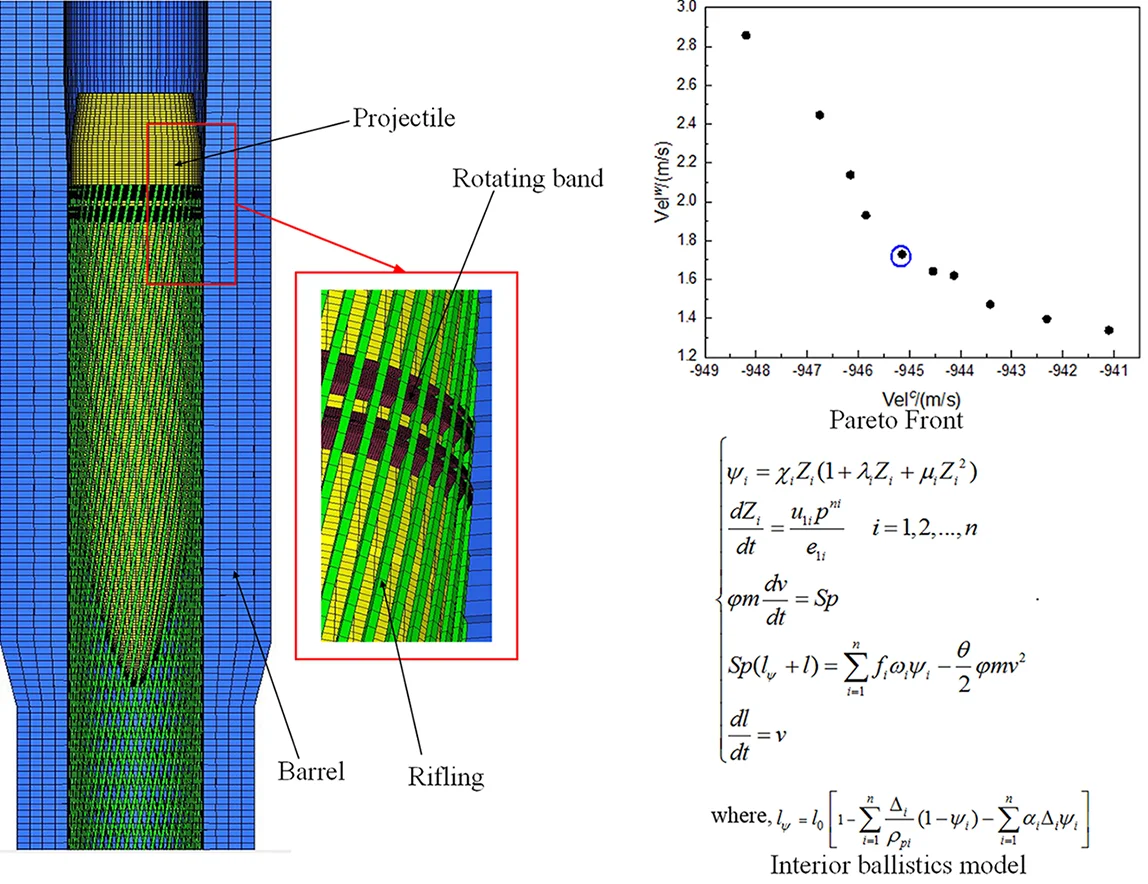
The gun barrel, projectile and rotating band were modeled discretized. Except for a few wedge-shaped elements at the front of the rotating band, the hexahedral elements with eight nodes were adopted. The deformation of the gun barrel and the projectile is small, so the mesh of this part is large. Influenced by the driving side force, the contact force between the rotating band and rifling is very large, so the mesh size of rotating band should be small. The mesh model is shown in Fig. 1.

Fig. 1Finite element mesh model

2.2. Interior ballistic model

In the process of projectile motion in the chamber, the energy required for motion is provided by the combustion of the propellant. In order to describe the impact of propellant, an interior ballistic amplitude subroutine (VUAMP) is written to provide the driving force for the projectile. The interior ballistic model adopted the classical interior ballistic model based on thermodynamics, and its mathematical model is shown in Eq. (1):

1

\{\begin{array}{l} ψ_{i} = χ_{i} Z_{i} (1 + λ_{i} Z_{i} + μ_{i} {Z_{i}}^{2}), \\ \frac{d Z_{i}}{d t} = \frac{u_{1 i} p^{n i}}{e_{1 i}}, i = 1,2, . . ., n, \\ φ m \frac{d v}{d t} = S p, \\ S p (l_{ψ} + l) = \sum_{i = 1}^{n} f_{i} ω_{i} ψ_{i} - \frac{θ}{2} φ m v^{2}, \\ \frac{d l}{d t} = v, \end{array}

where, $l_{ψ} = l_{0} [1 - \sum_{i = 1}^{n} \frac{Δ_{i}}{ρ_{p i}} (1 - ψ_{i}) - \sum_{i = 1}^{n} α_{i} Δ_{i} ψ_{i}]$ . $i$ is the number of composite charge, $χ_{i}$ , $λ_{i}$ and $μ_{i}$ are charge form coefficient, $m$ is the mass of projectile, $ω_{i}$ is the mass of charge, $S$ is the equivalent cross-sectional area, $φ_{i}$ is the coefficient of second work, $l_{0}$ is the chamber volume-to-bore area ratio, $l_{ψ}$ is the free chamber volume-to-bore area ratio, $p$ is the propellant gas pressure, $α_{i}$ is the co-volume and $l$ and $v$ are the displacement and velocity of projectile respectively.

In the above formula, the burned thickness $Z$ can be solved by the fourth-order Runge-Kutta method to solve the differential equation. The velocity and displacement of the projectile can be directly obtained by the sensor in ABAQUS, and the combination of the two can solve the chamber pressure. The specific execution process is as follows: the initial chamber pressure is obtained through the initial parameters of the interior ballistic, which pushes the projectile forward at the bottom; the velocity and displacement of the projectile can be read directly by the sensor in ABAQUS as the initial conditions for the next calculation to calculate the next chamber pressure, and so on until the projectile is out of the muzzle. At this point, the artillery in-bore launching model was established. This model can be used to calculate the parameters needed for optimization.

3. Uncertain optimization method for artillery in-bore launching performance based on interval optimization

There are generally three uncertain optimization methods: probability model [2], fuzzy model [3] and interval model [4]. The interval model is based on interval mathematics and interval programming. The uncertain variables are regarded as the upper and lower intervals of the uniform distribution. It is not necessary to know the probability distribution of the parameters or the fuzzy membership function. Therefore, this paper chooses the interval method to optimize the uncertainty.

The interval uncertain optimization problem can be expressed as:

2

\begin{array}{l} m i n f (X), \\ s . t . g_{i} (X) \leq (=, \geq) {b_{i}}^{I} = [b^{L}, b^{R}], i = 1,2, . . ., k, \\ X \in X^{I} = [X^{L}, X^{R}] = ⟨X^{c}, X^{w}⟩, X_{i} \in {X_{i}}^{I} = [X^{L}, X^{R}], i = 1,2, . . ., n, \end{array}

where $X$ denotes an uncertainty interval vector, which is composed of an $n$ -dimensional interval vector $X^{I}$ . the superscripts $L$ , $R$ , $c$ and $w$ represent the lower, upper, center, and radius of the interval, respectively. $f$ and $g$ denote the uncertain objective function and uncertain constraints of the interval optimization, respectively. Due to the transitivity of uncertain factors, objective function and constraints also interval numbers rather than real numbers.

3.1. Uncertain design variables

The uncertain design variables considered in this paper include the following three categories (totaling 10). The initial values and ranges of the design variables are listed in Table 1.

a) Projectile parameters: rotating band location $l_{d}$ , rotating band width $H$ , mass eccentricity $e_{0}$ , CM (center of mass) axial location from shell base $l_{R}$ , projectile radius $d$ .

b) Barrel structure parameters: rifling depth $t$ , groove engravings width $b$ , chamber volume $W_{0}$ .

c) Propellant charge parameters: web thickness 2 $e_{1}$ , propellant mass $ω$ .

Table 1Initial values and ranges of design variables

Parameter	$l_{d}$ (mm)	$H$ (mm)	$e_{0}$ (mm)	$l_{R}$ (mm)	2 $e_{1}$ (mm)
Initial	50.0	27.0	0.0	510.0	2.2
Lower	55.0	30.0	0.0	532.0	2.1
Upper	60.0	33.0	0.5	550.0	2.4
Parameter	$d$ (mm)	$t$ (mm)	$b$ (mm)	$W_{0} (L)$	$ω$ (kg)
Initial	76.3	2.325	6.5	26.0	17.0
Lower	74.0	2.325	5.9	25.0	16.4
Upper	77.4	3.1	6.9	27.0	18.0

3.2. Treatment of the uncertain objective function

In interval optimization, interval order relations are often used to qualitatively determine whether an interval is better or worse than another interval. In this paper, the interval order relation $\leq_{c w}$ proposed by Jiang [5] was adopted to deal with uncertain objective functions. $A^{I} \leq_{c w} B^{I}$ means that interval $B$ is better than interval $A$ only when the radius and midpoint of interval $B$ are both smaller than interval $A$ . Therefore, the uncertain objective function of Eq. (2) can be transformed into the following multi-objective optimization problem:

3

\begin{array}{l} \underset{X}{m i n} (f^{c} (X), f^{w} (X)), \\ f^{c} (X) = \frac{[f^{R} (X) + f^{L} (X)]}{2}, f^{w} (X) = \frac{[f^{R} (X) - f^{L} (X)]}{2}, \end{array}

where, $f^{R} (X)$ and $f^{L} (X)$ are upper and lower bounds of the objective function respectively.

3.3. Treatment of the uncertain constraints

For the uncertain constraints in Eq. (2), Jiang C. [5] proposed an improved interval probability degree model to compare the two intervals:

4

P (A^{I} \leq B^{I}) = \{\begin{array}{l} 0, A^{L} \geq B^{R}, \\ \frac{B^{R} - A^{L}}{2 (A^{R} - A^{L})} \frac{B^{R} - A^{L}}{B^{R} - B^{L}}, B^{L} \leq A^{L} < B^{R} \leq A^{R}, \\ \frac{B^{L} - A^{L}}{A^{R} - A^{L}} + \frac{B^{R} - A^{L}}{2 (A^{R} - A^{L})}, A^{L} < B^{L} < B^{R} \leq A^{R}, \\ \frac{B^{L} - A^{L}}{A^{R} - A^{L}} + \frac{A^{R} - B^{L}}{A^{R} - A^{L}} \frac{B^{R} - A^{R}}{B^{R} - B^{L}} + \frac{A^{R} - B^{L}}{2 (A^{R} - A^{L})} \frac{A^{R} - B^{L}}{B^{R} - B^{L}}, A^{L} < B^{L} \leq A^{R} < B^{R}, \\ \frac{B^{L} - A^{L}}{A^{R} - A^{L}} + \frac{B^{R} - A^{L}}{2 (A^{R} - A^{L})}, B^{L} \leq A^{L} < A^{R} < B^{R}, \\ 1, A^{R} < B, \end{array}

where $P (A^{I} \leq B^{I})$ or $P (A^{I} \geq B^{I})$ is the probability of a random variable of interval $A$ being smaller or larger than interval $B$ . The uncertain constraints are transformed into deterministic constraints by the interval probability degree model in Eq. (4).

The inequality constraint of type $\leq$ , such as ${g_{i}}^{I} (X) \leq {b_{i}}^{I}$ , can be transformed into the following deterministic constraint:

5

P ({g_{i}}^{I} (X) \leq {b_{i}}^{I}) \geq λ_{i},

where, $λ_{i}$ denotes the interval possibility degree value set by the decision maker. Larger value of $λ_{i}$ indicates stricter constraints.

The inequality constraint of type =, such as ${g_{i}}^{I} (X) = {b_{i}}^{I}$ , can be transformed into the following two deterministic constraint:

6

P ({g_{i}}^{I} (X) \geq {b_{i}}^{L}) \geq λ_{i}, P ({g_{i}}^{I} (X) \leq {b_{i}}^{R}) \geq λ_{i} .

Through the above treatment, the interval uncertain optimization problem expressed in Eq. (2) can be converted into the following deterministic optimization problem:

7

\begin{array}{l} m i n (f^{c} (X), f^{w} (X)), \\ s . t . P ({g_{i}}^{I} (X) \leq (=, \geq) {b_{i}}^{I}) \geq λ_{i}, i = 1,2, . . ., k, \\ X \in X^{I} = [X^{L}, X^{R}] = ⟨X^{c}, X^{w}⟩, X_{i} \in {X_{i}}^{I} = [X^{L}, X^{R}], i = 1,2, . . ., n, \end{array}

where:

f^{c} (X) = \frac{[f^{R} (X) + f^{L} (X)]}{2}, f^{w} (X) = \frac{[f^{R} (X) - f^{L} (X)]}{2} .

From the perspective of launch safety and gun performance, the maximum chamber pressure $P_{m a x}$ and muzzle velocity $V e l$ are selected as constraint and objective function respectively. The maximum chamber pressure and projectile velocity can be obtained by finite element model. Thus, the following deterministic multi-objective optimization model is obtained:

8

\begin{array}{l} m i n (- V e l^{c} (X), V e l^{w} (X)), \\ s . t . P (310 \leq {P_{m a x}}_{i}^{I} (X) \leq 340) \geq λ = 0.99, \\ X \in X^{I} = [X^{L}, X^{R}], \end{array}

V e l^{c} (X) = \frac{[V e l^{R} (X) + V e l^{L} (X)]}{2}, V e l^{w} (X) = \frac{[V e l^{R} (X) - V e l^{L} (X)]}{2} .

The above problem is a two-layer nested optimization problem. The inner optimizer is used to solve the upper and lower bounds of uncertain objective functions and constraints. The outer optimizer is used to search for optimal design variable. Considering that there are two objective functions in Eq. (8), NSGA-II is used to solve the optimal solution. The inner optimizer is the GA. Although the GA has a strong global search capability, its needs too much computation.

In addition, for the artillery in-bore launching model established in this paper, using actual simulation model for nested optimization will bring unacceptable computation cost. In order to solve the contradiction between computational accuracy and computational efficiency, BP neural networks are adopted to replace the initial model. The above method is illustrated in Fig. 2.

Fig. 2Optimization flowchart

4. Optimization results

A set of non-dominated solutions organized in a Pareto-optimal front is illustrated in Fig. 3. As can be seen from the Fig. 3, as the midpoint of the velocity interval increases, the radius of the interval also increases, which indicates that blindly pursuing high muzzle velocity of the projectile will lead to large velocity fluctuation. Therefore, in order to give consideration to the high muzzle velocity and robustness, point A in the figure $X$ is selected as the final design scheme. The interval of each design variable is obtained and the results are listed in Table 2.

Fig. 3Pareto front

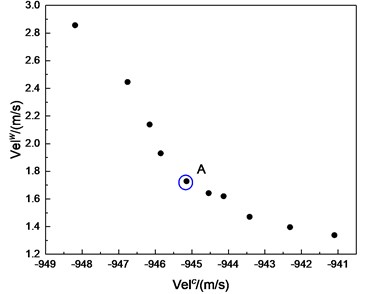
Table 2Intervals of the design variables

Parameter	$l_{d}$ (mm)	$H$ (mm)	$e_{0}$ (mm)	$l_{R}$ (mm)	2 $e_{1}$ (mm)
$X^{c}$	55.5998	26.8069	0.1749	529.1584	2.1164
$X^{w}$	0.0823	0.0487	0.0021	5.6190	0.0023
$X^{L}$	55.5175	26.7582	0.1728	523.5394	2.1141
$X^{R}$	55.6821	26.8556	0.177	534.7774	2.1187
Parameter	$d$ (mm)	$t$ (mm)	$b$ (mm)	$W_{0} (L)$	$ω$ (kg)
$X^{c}$	76.1279	2.8315	6.2591	26.8069	17.9413
$X^{w}$	0.0014	0.0023	0.0017	0.0487	0.0832
$X^{L}$	76.1265	2.8292	6.2574	26.7582	17.8581
$X^{R}$	76.1293	2.8338	6.2608	26.8556	18.0245

5. Conclusions

In this paper, the interval uncertain optimization theory is utilized to research the artillery in-bore launching performance uncertain optimization problem. Reasonable ranges of projectile, gun barrel and propellant charge parameters are obtained. The midpoint of the interval in the optimization result can be regarded as nominal size, and the interval radius can be regarded as tolerance range. It can be used as a reference in the design of artillery weapon system.

References

Wang L., et al. An uncertain optimization method for overall ballistics based on stochastic programming and a neural network surrogate model. Engineering Optimization, Vol. 51, Issue 4, 2018, p. 663-679.

Publisher
Ke H., Su T., Ni Y. Uncertain random multilevel programming with application to production control problem. Soft Computing, Vol. 19, Issue 6, 2014, p. 1739-1746.

Publisher
Luhandjula M. K. Fuzzy optimization: Milestones and perspectives. Fuzzy Sets and Systems, Vol. 274, 2015, p. 4-11.

Publisher
Jiang C., Han X., Liu G. P. A sequential nonlinear interval number programming method for uncertain structures. Computer Methods in Applied Mechanics and Engineering, Vol. 197, Issues 49-50, 2008, p. 4250-4265.

Publisher
Jiang C., et al. A nonlinear interval number programming method for uncertain optimization problems. European Journal of Operational Research, Vol. 188, Issue 1, 2008, p. 1-13.

Publisher

Cited by

Uncertain optimization for initial disturbance of projectile for moving tank based on stochastic programming and deep learning surrogate model

(2024)

About this article

Received

18 September 2019

Accepted

26 September 2019

Published

19 October 2019

SUBJECTS

Mathematical models in engineering

DOI

https://doi.org/10.21595/vp.2019.21030

Keywords

larger-caliber artillery

uncertain optimization

interior ballistic

interval optimization

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 04 04

Launching dynamics of terminal guidance projectile considering barrel erosion and mechanical wear

Cheng Yuan Guo, Li Qun Wang, Guo Lai Yang

Research article

2023 11 25

The effect of ambient temperature on the internal ballistic overload of a large-caliber artillery projectile fuze system

Zilong Yang, Deren Kong, Chunyan Zhang

Research article

2023 05 18

Uncertain optimization for composite base plate of mortar under impact load

Fengfeng Wang, Guolai Yang, Fengjie Xu

Research article

2022 08 25

Numerical analysis of projectile-based low overload launch model

Zhiyi He, Guolai Yang

F. Xu and G. Yang, “Uncertain optimization of in-bore launching performance of artillery based on interval method,” Vibroengineering PROCEDIA, Vol. 28, pp. 189–194, Oct. 2019, https://doi.org/10.21595/vp.2019.21030

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2019.21030
UR  - https://doi.org/10.21595/vp.2019.21030
TI  - Uncertain optimization of in-bore launching performance of artillery based on interval method
T2  - Vibroengineering PROCEDIA
AU  - Yang, Guolai
AU  - Xu, Fengjie
PY  - 2019
DA  - 2019/10/19
PB  - JVE International Ltd.
SP  - 189-194
VL  - 28
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Yang_2019,
	doi = {10.21595/vp.2019.21030},
	url = {https://doi.org/10.21595/vp.2019.21030},
	year = 2019,
	month = {oct},
	publisher = {{JVE} International Ltd.},
	volume = {28},
	pages = {189--194},
	author = {Guolai Yang and Fengjie Xu},
	title = {Uncertain optimization of in-bore launching performance of artillery based on interval method},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]G. Yang and F. Xu, “Uncertain optimization of in-bore launching performance of artillery based on interval method,” Vibroengineering PROCEDIA, vol. 28, pp. 189–194, Oct. 2019, doi: 10.21595/vp.2019.21030.

Copy IEEE

Copied to clipboard!

Yang, Guolai, and Fengjie Xu. “Uncertain Optimization of In-Bore Launching Performance of Artillery Based on Interval Method.” Vibroengineering PROCEDIA 28 (October 19, 2019): 189–94. https://doi.org/10.21595/vp.2019.21030.

Copy Chicago

Copied to clipboard!

Uncertain optimization of in-bore launching performance of artillery based on interval method

Abstract

Highlights

1. Introduction

2. Artillery in-bore launching model

2.1. Finite element mesh model

2.2. Interior ballistic model

3. Uncertain optimization method for artillery in-bore launching performance based on interval optimization

3.1. Uncertain design variables

3.2. Treatment of the uncertain objective function

3.3. Treatment of the uncertain constraints

4. Optimization results

5. Conclusions

References

Cited by

About this article

Related Articles