Study on reversal and lateral vibration in the stepped well

Han, Chunjie; Guo, Ming; Wang, Xiangxu; Yan, Tie; Jing, Guolin

doi:10.21595/jve.2020.21046

Journal of Vibroengineering

Browse Journal

Submit article

Published: 03 September 2020

Check for updates

Study on reversal and lateral vibration in the stepped well

Chunjie Han¹

Ming Guo²

Xiangxu Wang³

Tie Yan⁴

Guolin Jing⁵

^{1, 2, 3}School of Electronic Science, Northeast Petroleum University, Daqing, 163318, China

⁴School of Petroleum Engineering, Northeast Petroleum University, Daqing, 163318, China

⁵School of Chemistry and Chemical Engineering, Northeast Petroleum University, Daqing, 163318, China

Corresponding Author:

Ming Guo

Cite the article Download PDF

Downloads 936

Abstract

The reversal and lateral vibration of the drill string are very complex motion and can affect the normal operation of the drill string. The movement of the drill string in the stepped well is different from the movement of the drill string in the regular well. The vibration of the drill string in the stepped well varies with the size of the wellbore and can be visually reflected by the phase speed. To find out the relationship between reversal and lateral vibration, the natural frequency of lateral vibration of the drill string was solved by using the method of energy conservation. The analysis shows that the phase speed of flexural wave in the stepped well is faster in small size wellbore than in large size wellbore. The reversal and lateral resonance is easy to happen in small size wellbore, and the reversal will excite lateral vibration. When the sum of reversal and rotational angular frequencies approaches the natural angular frequency of lateral vibration, the lateral resonance will occur.

Study on reversal and lateral vibration in the stepped well

1. Introduction

In the process of petroleum drilling, drill string system plays an important role. Appropriate vibration of the drill string is beneficial to clear the bottom cuttings, to improve the rock-breaking efficiency and reduce the sliding friction [1-5]. The reversal and lateral vibration of the drill string in the stepped well is more complicated than that in the regular well. Drill string vibration is one of the most important criteria to measure the performance of drill string system. When the sum of the rotational and reversal angle frequencies of the drill string is close to the lateral vibration natural angular frequency, the lateral resonance will occur [6, 7]. Collision and pressure will cause serious wear in drill string. To better understand the characteristics of the reversal and lateral vibration in the stepped well and prevent the lateral resonance of the drill string, it is necessary to study the relationship between reversal and lateral vibration.

At present, scholars have made many important achievements in the research of reversal and lateral vibration. Jansen [8, 9] studied the lateral vibration of the drill string caused by rotational contact with the wellbore wall, then he designed a control system to reduce lateral vibration, but this system ignored the axial force. Han [10] studied the nature frequency of lateral vibration of the drill string. She concluded that the nature frequency of lateral vibration of the drill string was related to the nature of itself and the axial force exerted. Lian [11] discussed the reversal motion of the drill string and bending frequency, he found that there was not only the rotation but also the reversal in the drill string. The drill string bending frequency was the sum of the drill string rotational speed and the reversal rotational speed. Reversal rotational speed was related to the annulus ratio. Zamani et al. [12] made a review of the drill string failure. They collected and summarized a lot of drill string failure cases, and found that overloading of tension and torque failures accounted for 85 % of total drill string failures. Lin [13] analyzed the failure of oilfield drilling tools showed that most of the failures of drilling tools were due to the reversal and lateral resonance of the drill string. Han and Yan [14] established the lateral vibration equation of drill string in the presence of axial load, and the nature frequency of lateral vibration of the drill string was obtained, and concluded that the reversal of the drill string was an important factor to stimulate the lateral vibration. Tian et al. [15] discussed the effect of lateral inertia on lateral vibration of the drill string. The natural frequency of lateral vibration of the drill string was higher than that without considering the lateral inertia, and the natural frequency gradually decreased with the increasing of drill string length.

The application of stepped wells in practice is very important, but no scholars currently have studied the drill string reversal and lateral vibration in stepped wells. Because of the complexity of reversal and lateral vibration in stepped wells, research on reversal and lateral vibration in stepped wells is necessary. In this paper, the characteristics of reversal of the drill string in the stepped well was researched, and the phase speed was used to illustrate the vibration of the drill string in the well. Most scholars selected the infinitesimal of the drill string and established a mechanical equilibrium equation, and substituted boundary conditions into the established equation to obtain the natural frequency of the drill string. In this article, we used the principle of energy conservation, the kinetic energy of the drill string was equal to the portion of the energy converted into potential energy, and established the lateral vibration model of the drill string and solved the natural frequency of lateral vibration of the drill string. By the example analysis of the failures of the drill string, the relationship between the reversal and lateral vibration in the stepped well was found out.

2. Reversal of drill string

When the drill string rotates around the axis in the clockwise direction with the rotational speed of the turntable, the joints of the drill string attaches to the well wall due to the centrifugal force. Under the action of the friction between the drill string joint and the well wall, the drill string will rotate around the wellbore axis in the counterclockwise direction along the well wall at a certain speed. It is like the rotational wheel or pipe is rolling forward at a certain speed on the flat ground, but now the ground is replaced by the well wall. This is shown in Fig. 1.

Fig. 1Diagram of drill string reversal (top view)

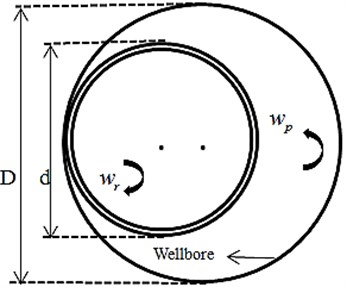
When the drill string joint is rolling along the well wall without sliding, the reversal angular speed of the drill string has the following relationship with the angular speed of the turntable.

Annulus ratio can be expressed as:

1

β = \frac{d}{D - d} .

Relationship between reversal and rotational angular speed of the drill string is:

2

ω_{p} = β ω_{r} .

Relationship between reversal and rotational speed of the drill string is:

3

n_{p} = β n_{r} .

2.1. Measured value in stepped well

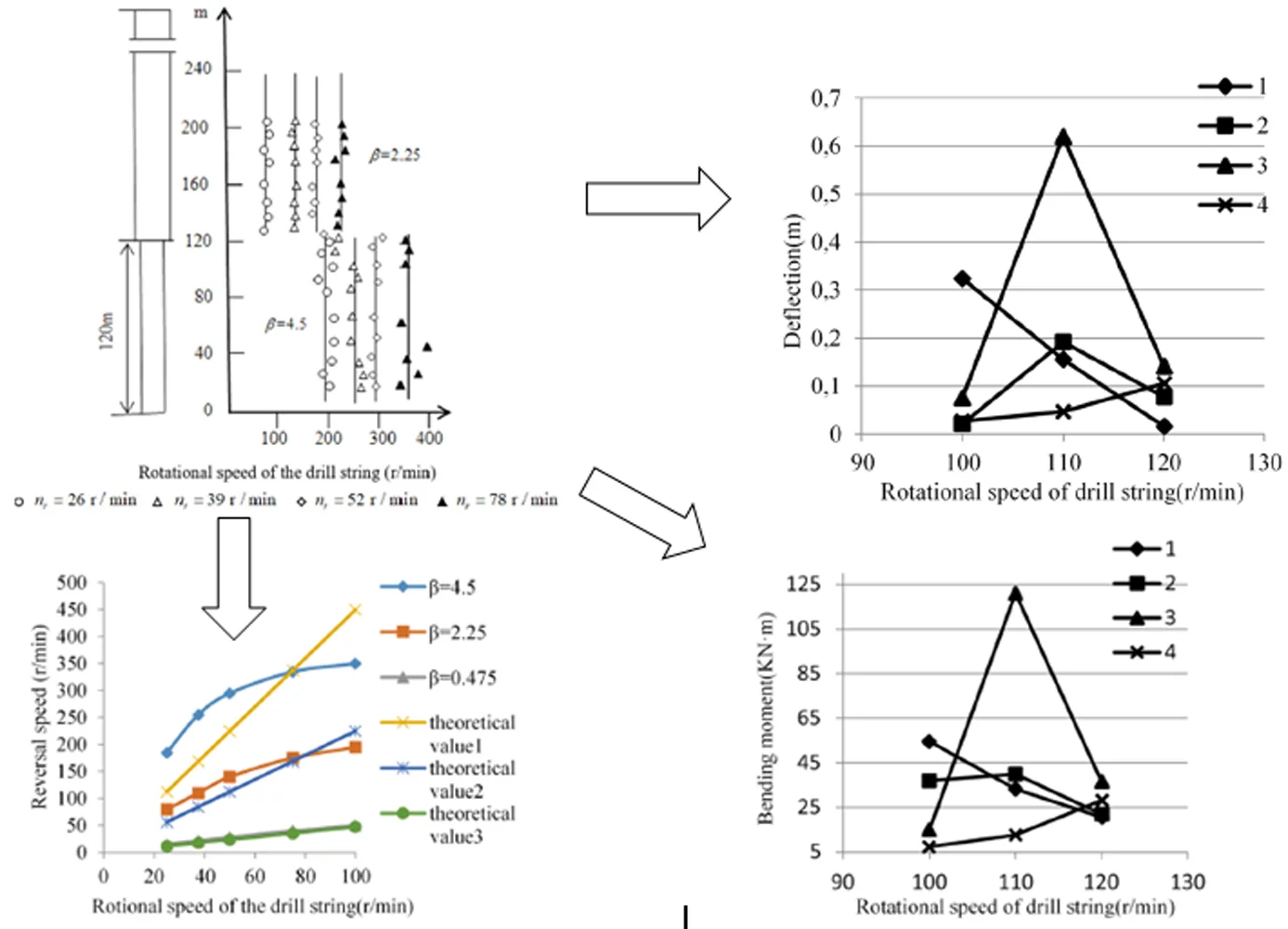
The simulated drill string was developed based on theoretical derivation and selection of materials in our university^’s laboratory. The simulated drill string is a reduced ground drill string model. Wellbore was simulated with transparent polymethyl methacrylate tube [16-18]. The movement of the drill string can be observed and measured by using this simulated drill string system on the ground. The geometric similarity ratio between the simulated drill collar and the actual drill collar was 1: 12.55, and the similarity ratio between the simulated drill string rotational speed and the actual rotational speed was 3.54: 1. By the instrument installed in the model, we measured the reversal trajectory and time of the drill string, and the drill string reversal speed was calculated. We measured the reversal speed of the drill string joint in the stepped well by the manufactured experimental. Fig. 2 shows a model diagram based on measured values.

Fig. 2Reversal rotational speed of joints of drill string in the stepped well

As shown in Fig. 2, the solid lines shows the theoretical values, and the break points shows the measured values of drill string joints. When the value of $β$ is small, the measured value is concentrated near the theoretical value. When the value of $β$ is large, the measured value is scattered. The reversal rotational speed in the small size well is high, but the reversal rotational speed in the large size well is low. Most of the upper and lower joints of the same drill string has different reversal speed in the same size stepped well. And when the same drill string rotates in two different size stepped wells, rotational speed is different in drill string joints. Especially at 120 meters of stepped well, the upper joint of a drill string is in the large size wellbore and the lower joint is in the small size wellbore. When the turntable speed is 40 r/min, the upper joint reversal speed is 88 r/min, and the lower joint reversal speed is 202 r/min. The difference of reversal speed of the two joints is particularly large. Therefore, when the drill string is drilled in a stepped wellbore and a wellbore with an irregular diameter wellbore, the drill string reversal motion will demonstrate very complicated.

2.2. Characteristics of reversal in stepped well

The rotational drill string is usually a complex multi-point self-excited lateral vibration system, so the reversal trajectory of the drill string is generally not circular and no obvious pattern. The relationships between the theoretical value and the measured value of reversal of drill string in stepped well is shown in Fig. 3.

The curve shows the measured value and the straight line shows the theoretical value. The theoretical values 1, 2 and 3 are calculated under the conditions that the values of $β$ are 4.5, 2.25 and 0.475. The reversal motion has a close relationship with the annulus ratio and the rotational speed of the drill string, the larger the annulus ratio and the higher the rotational speed of the drill string, the easier it is to reverse [19].

Fig. 3The relationships between theoretical and the measured value of reversal of the drill string

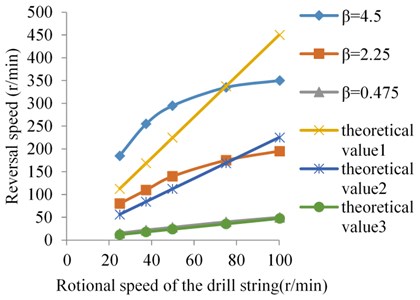
Fig. 3 shows that the measured value basically does not match the theoretical value. With the annulus ratio increasing, the measured value was deviated from the theoretical value. When the value of $β$ is 0.475, the rotational speed of the drill string is close to the theoretical value. As the value of $β$ increasing, the experimental value and the theoretical value begin to deviate. There is a intersection point of the solid line and the broken line, and the reversal rotational speed of the drill string conforms to the measured value at the intersection point.

Combining Fig. 2 with Fig. 3, the measured value before the intersection point is bigger than the theoretical value of reversal, and the measured value is equal to the theoretical value at the intersection point, and the measured reversal speed is less than the drill string speed after the intersection point. This is because when the rotational speed of the drill string is lower than the rotational speed of the drill string at the intersection, the drill string joints does not always keep in contact with the well wall due to the small centrifugal force, and the actual drill string reversal is accompanied by sliding, and often jumps away from the well wall. Therefore, the radius of gyration of the drill string around the axis of the wellbore is shrunk, and the measured value is larger than the theoretical value. At the intersection point, the measured value is equal to the theoretical value, that is because when the drill string contacts with the wellbore and roll, there is the reversal and no sliding at this point. After the intersection point, the drill string joints always keep in contact with the well wall due to the large centrifugal force. Meanwhile, the reversal of the drill string around the wellbore will increase the alternating stress on the drill string, and the higher rotational speed, the greater alternating stress is. Because of unstable centrifugal force, drill string joint knocks the well wall strongly. The impulsive rebound force of the borehole wall on the drill string resists the reversal motion, so the measured value is lower than the theoretical value.

The vibration of the drill string in the stepped well also can be reflected from the phase speed of the flexural wave. If the wave of lateral vibration can be detected, the drill string is in a strong vibration state. The characteristics of flexural wave are different in different sections of stepped well. When the drill string rotates, it looks like a gyro. The radius of gyration of gyro can be expressed as:

4

R_{F} = \sqrt{\frac{I}{A}} .

The axial speed of drill string can be expressed as:

5

V_{a} = \sqrt{\frac{E}{ρ_{s}}} .

The phase speed of flexural wave can be expressed as:

6

V_{p} = \sqrt{R_{F} V_{a} ω} .

3. The natural frequency of lateral vibration of drill string

Assuming that the drill string is under ideal conditions in the following analysis. The speed of the drilling fluid is not considered, and the effects of longitudinal and torsional vibration of drill string on lateral vibration of drill string are neglected. Model of drill string under external excited force is shown in Fig. 4.

Fig. 4The bending mechanical model of drill string with external excited force

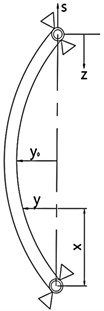
The relationship between $x$ and $y$ is:

7

y = y_{0} s i n n π \frac{x}{l},

8

P_{m a x} = \frac{1}{2} \int {\dot{y}}_{m a x} d m = \frac{1}{2} ω^{2} \int y^{2} d m .

Eq. (8) satisfies the boundary conditions of zero deflection and bending moment at $x = 0$ and $x = l$ .

Thus:

9

P_{m a x} = \frac{1}{2} ω^{2} \int y^{2} d m = \frac{1}{2} \int_{0}^{l} y^{2} \frac{m}{l} d x = \frac{m}{4} ω^{2} {y_{0}}^{2} .

where:

10

K_{m a x} = \frac{1}{2} {\int E I (\frac{d^{2} y}{d x^{2}})}^{2} d x + z S,

11

\frac{1}{2} {\int E I (\frac{d^{2} y}{d x^{2}})}^{2} d x = \frac{E I}{4} \frac{n^{4} π^{4}}{l^{3}} {y_{0}}^{2},

12

z = \int_{0}^{l} (\sqrt{(1 + {(\frac{d y}{d x})}^{2})} - 1) d x = \int_{0}^{l} \frac{1}{2} {(\frac{d y}{d x})}^{2} d x .

Combining Eq. (11) and Eq. (12), we obtain:

13

K_{m a x} = (\frac{E I}{4} \frac{n^{4} π^{4}}{l^{3}} + \frac{S}{4} \frac{n^{2} π^{2}}{l}) {y_{0}}^{2} .

Thus:

14

{ω_{n}}^{2} = \frac{(\frac{E I}{4} \frac{n^{4} π^{4}}{l^{3}} + \frac{S}{4} \frac{n^{2} π^{2}}{l})}{\frac{m}{4}} .

Because:

15

m = ρ_{s} A l .

Therefore:

16

ω_{n} = {(\frac{n π}{l})}^{2} \sqrt{\frac{E I}{ρ_{s} A}} \sqrt{1 + \frac{S}{{(\frac{n π}{l})}^{2} E I}} .

According to Eq. (16), the natural angular frequency of the lateral vibration is related to the nature of the drill string and the axial force exerted.

Eq. (17) and Eq. (18) are for calculating the deflection and bending moment [20]:

17

δ = 1.268 \frac{R_{1} \frac{{ω_{p}}^{2}}{{ω_{1}}^{2}}}{1 - [\frac{(ω_{p} + ω_{r})^{2}}{{ω_{1}}^{2}}]},

18

M = \frac{γ A R_{1} {ω_{p}}^{2} {L_{1}}^{2}}{8 g} \{1 + 1.032 \frac{\frac{(ω_{p} + ω_{r})^{2}}{{ω_{1}}^{2}}}{|1 - [\frac{(ω_{p} + ω_{r})^{2}}{{ω_{1}}^{2}}]|}\} .

From Eq. (17), when the sum of the rotational and reversal angular frequency is greater than the natural angular frequency of the first order, the deflection would be a negative number, and the negative sign means that the direction of vibration is opposite to the positive y-axis. For ease of comparison that all deflection values obtained in the example are taken as absolute values.

4. Case analysis

4.1. Case 1

With the funding of this project, we carried out on-site inspections of Fuyang No.1 well in Donghai, Shengping No.1 well in Donghe Daqing and 1-H3 double-step wells in Tarim Xinjiang. We found out there was an 86 % agreement by comparing our theoretical research with field data. Our theory also guided field experiments, and proved to be extremely available.

Table 1 shows the various parameters of 1-H3 double-step wells in Tarim Xinjiang. Combining Eq. (6) with Eq. (16), the phase speed in the stepped well was calculated, the results are shown in Table 2.

From the calculating results in Table 2, it shows that the phase speed in the stepped well propagates faster in the small size wellbore than that in the large size wellbore. The less the number of the drill string involved in lateral vibration, the faster the phase speed is. This result is caused by the fact that the energy is generated by the vibration of the drill strings. The energy propagates back and forth between the drill string joints, but the energy cannot be released quickly. By detecting the phase speed, the lateral vibration of the drill string in the stepped well can be analyzed. From Case 1, the first-order natural frequency of the lateral vibration in the large size wellbore is smaller than that in small size wellbore, so the drill string is easier to lateral resonance in small size wellbore of the stepped well. By oil file data, it was found that the number of drill strings that failed was due to overloading in the small size wellbore was greater than that in the large size wellbore.

Table 1Calculating parameters

Parameter name	Parameter values
Diameter of drill string $d$ / (mm)	89
Thickness of drill string $t$ / (mm)	9
Well depth $h$ / (m)	1400
Density of drill string $ρ_{s}$ / (kg/m³)	7850
Density of drilling fluid $ρ_{f}$ / (kg/m³)	1200
Gravity acceleration $g$ / (m/s²)	10
Elastic modulus $E$ / (GPa)	206

Table 2Relationships between phase speed and annulus ratio in stepped wells

Annulus ratio	Vibration length (m)	Natural frequency (rad/s)	Phase speed (m/s)
$β =$ 2.25	80	2.36	19
$β =$ 2.25	120	1.55	15.4
$β =$ 2.25	160	1.14	13.2
$β =$ 4.5	8	21.4	57
$β =$ 4.5	16	10.6	40.3
$β =$ 4.5	32	5.4	28.8

4.2. Case 2

Table 3 shows the various parameters of the drill string of the Fu Yang No.1 Well in the East China Sea. The deflection and bending moment of the drill string at different rotational speed were analyzed. The relationship between the reversal and the lateral vibration is reflected by the specific data. The results are shown in Table 4.

Table 3Calculating parameters

Parameter name	Parameter values
Diameter of drill string $d$ / (mm)	20
Thickness of drill string $t$ / (mm)	102
Well depth $h$ / (m)	175
Density of drill string $ρ_{s}$ / (kg/m³)	7850
Density of drilling fluid $ρ_{f}$ / (kg/m³)	1200
Gravity acceleration $g$ / (m/s²)	10
Elastic modulus $E$ / (GPa)	206

Table 4Puncture points of different wells and their natural frequencies

Serial number	Well depth (m)	Distance from the point of the puncture to the wellhead (m)	Natural frequency (rad/s)
1	3271	145	24.7
2	3357	147	25.04
3	3780	125	26.8
4	4360	136	31.3

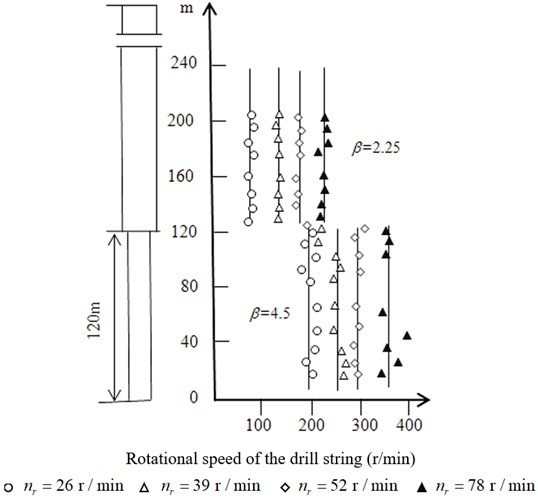
Fig. 5 shows the deflection and bending moment value in different rotational speed of drill string.

From Fig. 5, when the rotational speed is 110 r/min, the values of deflection and bending moment of the No. 3 are 5 to 10 times of that of the other three groups. Combine Eq. (17), it can be concluded that the reversal will induce lateral vibration of the drill string. When the rotational speed of drill string is 110 r/min, the sum of the rotational and reversal angular frequencies of the drill string is 26.4 rad/s, and the natural frequency of this point is 26.8 rad/s, so the drill string is nearly in lateral resonance. The single-sided annulus between the well wall and the joint is 0.0255 m, but the deflection value in the resonance is 0.620 m, so the drill string will have strong collision with the well wall, and the drill string will be subjected to the extremely strong reaction. Large bending stresses may cause puncture and other failures in the drill string in a short period of time.

In Case 2, the value of $β$ is 1.4. And the rotational speed of drill string are 100 r/min, 110 r/min and 120 r/min, so the sums of the rotational and reversal angular frequencies of the drill string in these three-speed are 24 rad/s, 26.4 rad/s and 28.8 rad/s. Combining Table 4 with Fig. 5, the closer the sum of the rotational and reversal angular frequencies to the natural frequency of lateral vibration of the drill string, the easier it is to stimulate lateral resonance in the drill string.

Fig. 5Deflection and bending moment of the puncture point at different speeds

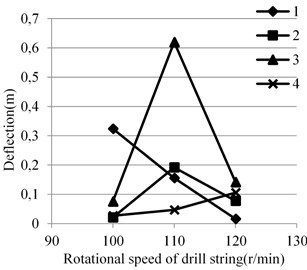
a)

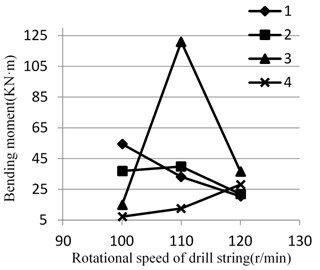
b)

5. Conclusions

1) Reversal of drill string at different sections in a stepped well is different. When the annulus ratio is small, the theoretical value and the measured value basically match. With the annulus rate increasing, the measured value begins to deviate the theoretical value.

2) From the phase speed, it can be seen that the phase speed of well sections with small annulus rate is small, and the phase speed of well sections with large annulus rate is large. The phase speed of flexural wave in the stepped well is faster in small size wellbore than in large size wellbore. The reversal and lateral resonance is easy to happen in small size wellbore.

3) The reversal will stimulate the lateral vibration of the drill string. The closer the sum of the drill string reversal and the rotational angle frequency to the natural angular frequency of the drill string, the easier it is to stimulate lateral resonance. Deflection and bending moment are important quantities to measure drill string failure. The lateral resonance of the drill string will cause serious damage in a short time, and the rotational speed of drill string should be adjusted, so that the sum of the drill string reversal and the rotational angle frequency is far from the natural angular frequency of lateral vibration of the drill string.

References

Wang Zhigang, Liang Jian, Liu Xiumei Analysis of failure behavior of drill string in deep geological core drilling. Exploration Engineering (Rock Soil Drilling and Tunneling), Vol. 45, Issue 12, 2018, p. 28-31, (in Chinese).

Search CrossRef
Wang Xiyou, Wang Chang, Xiong Jiyou, Xue chenggang, Long Gang Failure analysis of drilling tool leakage in tarim Oil field in 2005. Henan Petroleum, Vol. 1, 2006, p. 69-70, (in Chinese).

Search CrossRef
Chen Yaohui, Bi Xueliang, Yan Tie Analysis on drill string vibration of deep wells. Natural Gas Industry, Vol. 25, Issue 9, 2005, p. 76-79, (in Chinese).

Search CrossRef
Lan Kai, Liu Xiangfeng Research advances in drill string excessive vibration identification and control techniques. Journal of Jilin University (Geoscience Edition), Vol. 47, Issue 1, 2017, p. 203-214, (in Chinese).

Search CrossRef
Yang Jian-bo, Jiang Ping Study on fatigue life prediction of air drilling drill String. West-China Exploration Engineering, Vol. 21, Issue 4, 2009, p. 61-66, (in Chinese).

Search CrossRef
Yang C., Wang R., Han L., Xue Q. Analysis on the lateral vibration of drill string by mass effect of drilling fluid. Journal Mechanical Sciences, Vol. 10, 2019, p. 363-371.

Publisher
Li Dong-yang, Chen Cicang, Wang Qianqian An experimental study of drill string failure in gas drilling. China Petroleum Machinery, Vol. 40, Issue 7, 2012, p. 29-33, (in Chinese).

Search CrossRef
Jansen J. D., Van den Steen L. Active damping of self-excited torsional vibration in oil well drillstrings. Journal of Sound and Vibration, Vol. 179, Issue 4, 1995, p. 647-668.

Publisher
Jansen J. D. Non-linear rotor dynamic as applied to oil well drill string vibrations. Journal of Sound and Vibration, Vol. 147, Issue 1, 1991, p. 115-135.

Publisher
Han Chunjie, Yan Tie,Bi Xueliang Rules and their application of drilling string lateral vibration. Journal of Daqing Petroleum Institute, Vol. 1, 2004, p. 14-16, (in Chinese).

Search CrossRef
Lian Zhanghua, Luo FaQian, Liu Yuanyang Drill string reversal motion and bending frequency analysis. Journal of Southwest Petroleum Institute, Vol. 3, 2004, p. 75-78, (in Chinese).

Search CrossRef
Zamani S. M., Hassanzadeh Tabrizi S.-A., Sharifi H. Failure analysis of drill string: A review. Engineering Failure Analysis, Vol. 59, 2016, p. 605-623.

Publisher
Lin Yuanhua, Luo Faqian, Shi Taihe Reasons for failure of drilling tools in Tarim Oilfield. Drilling Production Technology, Vol. 5, 2007, p. 21-23, (in Chinese).

Search CrossRef
Han Chunjie, Yan Tie Study on the law of lateral vibration of drill string under reversal circumstance. Drilling and Production Technology, Vol. 1, 2007, p. 80-83, (in Chinese).

Search CrossRef
Tian Jialin, Wu Chunming, Yang Lin Study on lateral vibration characteristics of a drill string with lateral inertia effect. Journal of Failure Analysis and Prevention, Vol. 16, Issue 4, 2016, p. 678-682.

Publisher
Gee R., Hanley C., Hussain R., Canuel L., Martinez J. Axial oscillation tool vs. lateral vibration tools for friction reduction-what’s the best way to shake the pipe. SPE/IADC Drilling Conference and Exhibition, London, England, 2015.

Publisher
Altamimi Ibrahim M., Mokrani Samir, Zulkaf Ahmed H. Axial oscillation tool significantly mitigates the vibration level and enhances drilling performance in conjunction with standard RSS system. Abu Dhabi International Petroleum Exhibition and Conference, 2015.

Publisher
Jones Steve, Feddema Chad, Sugiura Junichi, Lightey Jeff A new friction reduction tool with axial oscillation increases drilling performance: field-testing with multiple vibration sensors in one drill string. IADC/SPE Drilling Conference and Exhibition, Fort Worth, Texas, 2016.

Publisher
Zhang Yanglie Kinematics and Dynamics of Drill String. Beijing, 2000, (in Chinese).

Search CrossRef

About this article

Received

20 September 2019

Accepted

12 June 2020

Published

03 September 2020

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/jve.2020.21046

Keywords

stepped well

drill string

reversal

lateral vibration

phase speed

natural frequency

deflection

bending moment

Acknowledgements

This work is supported by the National Major Special Project that Drilling Engineering Integration Software (No. 2016ZX05020-006). Great thanks to my teachers and classmates for their help during the writing process.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Next article in issue Next

Research article

2023 03 13

Vibration-collision mechanism of dual-stabilizer bottom hole assembly system in vertical wellbore trajectory

Pan Fang, Kang Yang, Gao Li, Qunfang Feng, Shujie Ding

Research article

2020 03 31

Dynamic analysis of the longitudinal vibration on bottom drilling tools

Chunxu Yang, Rui He Wang, Laiju Han, Qilong Xue

Research article

2020 03 31

Theoretical and experimental analysis of an unbalanced and cracked cardan shaft in the vicinity of the critical speed

Bernard Xavier Tchomeni, Alfayo Alugongo

Research article

2020 02 15

Effect of annulus drilling fluid on lateral vibration of drillstring

Chunxu Yang, Rui-He Wang, Laiju Han, Qilong Xue, Lixin Li

C. Han, M. Guo, X. Wang, T. Yan, and G. Jing, “Study on reversal and lateral vibration in the stepped well,” Journal of Vibroengineering, Vol. 22, No. 7, pp. 1548–1558, Sep. 2020, https://doi.org/10.21595/jve.2020.21046

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2020.21046
UR  - https://doi.org/10.21595/jve.2020.21046
TI  - Study on reversal and lateral vibration in the stepped well
T2  - Journal of Vibroengineering
AU  - Guo, Ming
AU  - Han, Chunjie
AU  - Wang, Xiangxu
AU  - Yan, Tie
AU  - Jing, Guolin
PY  - 2020
DA  - 2020/09/03
PB  - JVE International Ltd.
SP  - 1548-1558
IS  - 7
VL  - 22
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Guo_2020,
	doi = {10.21595/jve.2020.21046},
	url = {https://doi.org/10.21595/jve.2020.21046},
	year = 2020,
	month = {sep},
	publisher = {{JVE} International Ltd.},
	volume = {22},
	number = {7},
	pages = {1548--1558},
	author = {Ming Guo and Chunjie Han and Xiangxu Wang and Tie Yan and Guolin Jing},
	title = {Study on reversal and lateral vibration in the stepped well},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]M. Guo, C. Han, X. Wang, T. Yan, and G. Jing, “Study on reversal and lateral vibration in the stepped well,” Journal of Vibroengineering, vol. 22, no. 7, pp. 1548–1558, Sep. 2020, doi: 10.21595/jve.2020.21046.

Copy IEEE

Copied to clipboard!

Guo, Ming, Chunjie Han, Xiangxu Wang, Tie Yan, and Guolin Jing. “Study on Reversal and Lateral Vibration in the Stepped Well.” Journal of Vibroengineering 22, no. 7 (September 3, 2020): 1548–58. https://doi.org/10.21595/jve.2020.21046.

Copy Chicago

Copied to clipboard!

Study on reversal and lateral vibration in the stepped well

Abstract

1. Introduction

2. Reversal of drill string

2.1. Measured value in stepped well

2.2. Characteristics of reversal in stepped well

3. The natural frequency of lateral vibration of drill string

4. Case analysis

4.1. Case 1

4.2. Case 2

5. Conclusions

References

About this article

Related Articles