Mathematical modeling of the solution to the problem of plate bending given various fastenings along the contour and various loads

Toibayev, Serikbay; Uderbayeva, Assemgul; Bidakhmet, Zhanar; Rakhmatulina, Ayaulym; Zhauyt, Algazy

doi:10.21595/vp.2020.21343

Vibroengineering Procedia

Browse Procedia

Published: 26 November 2020

Check for updates

Mathematical modeling of the solution to the problem of plate bending given various fastenings along the contour and various loads

Serikbay Toibayev¹

Assemgul Uderbayeva²

Zhanar Bidakhmet³

Ayaulym Rakhmatulina⁴

Algazy Zhauyt⁵

^{1, 2, 3, 4}Department of Engineering Graphics and Applied Mechanics, Almaty Technological University, Almaty, 050012, Kazakhstan

⁵Department of Electronics and Robotic, Almaty University of Power Engineering and Telecommunications, Almaty, 050013, Kazakhstan

Corresponding Author:

Serikbay Toibayev

Cite the article Download PDF

Downloads 954

CrossRef Citations 1

Abstract

The classical equations of plate bending in various fastenings along the contour and various loads are considered. Using the decomposition method, three auxiliary problems are formulated to determine the deflection of the plate. The task is to determine the individual terms of the decomposition coefficients $a_{n m}^{(i)}$ from the individual terms of the load series. Then the system of algebraic equations is obtained to determine $a_{n m}^{(i)}$ . If the plate contour is pivotally fixed along the contour, then the system of equations takes a known form and the expression for the deflection function is explicitly found. Approximate analytical solutions are obtained for the functions of deflections, internal force factors and stresses under various boundary conditions of the plate.

1. Introduction

In our century, with the increasing complexity of the forms of building structures, the emergence of aircraft manufacturing, and the diverse demands of mechanical engineering, the role of elasticity theory methods has changed dramatically [1]. Now they form the basis for constructing practical methods for calculating deformable bodies and systems of bodies of various shapes [2]. At the same time, modern calculations take into account not only the complexity of the body shape and the variety of effects (power, temperature, etc.), but also the specificity of the physical properties of the materials from which the bodies are made [3]. The fact is that in modern designs along with traditional materials (steel, wood, concrete, etc.), new materials are widely used, in particular composites with a number of specific properties [4]. Thus, reinforcing polymers with fibers from high-strength materials makes it possible to obtain new lightweight structural material having high strength properties that exceed even the strength of modern steels [5]. But the presence of a polymer base gives such a composite material, viscous properties in addition to elasticity, which must be taken into account in the calculations [6]. Exact solutions in the analytical form of the equations of the elasticity theory subject to boundary conditions, which constitutes the so-called boundary value problem, are possible only in some special cases of loading bodies and the conditions for their fastening [7]. Therefore, for engineering practice, approximate, but fairly general methods for solving problems of the applied theory of elasticity are especially important [8].

2. Materials and methods

Consider a rectangular plate of constant thickness, having geometric dimensions in plan $0 \leq x \leq l_{1}$ , $0 \leq y \leq l_{2}$ . We assume that the plate along the contour in the general case is fixed elastically. To determine the bends, we have the differential equation describing the deformations:

1

D (\frac{\partial^{4} W}{\partial x^{4}} + 2 \frac{\partial^{4} W}{\partial x^{2} \partial y^{2}} + \frac{\partial^{4} W}{\partial y^{2}}) = q (x, y),

where $D = \frac{E_{1} δ^{3}}{12} = \frac{E δ^{3}}{12 (1 - μ^{2})}$ bending stiffness, $q (x, y)$ external load. Boundary conditions at elastic fastening of the plate along the contour:

2

\begin{array}{l} W = 0, l_{1} k \frac{\partial^{2} W}{\partial x^{2}} + (1 - k) \frac{\partial W}{\partial x} = 0, x = 0, x = l_{1}, \\ W = 0, l_{2} k \frac{\partial^{2} W}{\partial y^{2}} + (1 - k) \frac{\partial W}{\partial y} = 0, y = 0, y = l_{2} . \end{array}

Then boundary value problem Eq. (1) and Eq. (2) transform to the form ( $λ = l_{1} / l_{2}$ ):

3

\frac{\partial^{4} ν}{\partial α^{4}} + 2 λ^{2} \frac{\partial^{4} ν}{\partial α^{2} \partial β^{2}} + λ^{4} \frac{\partial^{4} ν}{\partial β^{4}} = \frac{q}{D} .

The purpose of the work is to determine the bending of the plate. In accordance with the decomposition method Eq. (3), we formulate three auxiliary problems:

Problem 1:

4

\frac{\partial^{4} ν^{(1)}}{\partial α^{4}} = f^{(1)} (α, β), ν^{(1)} = 0, π k \frac{\partial^{2} ν^{(1)}}{\partial α^{2}} + (1 - k) \frac{\partial ν^{(1)}}{\partial α} = 0, α = 0, α = π .

Problem 2:

5

λ^{4} \frac{\partial^{4} ν^{(2)}}{\partial β^{4}} = f^{(2)} (α, β), ν^{(2)} = 0, π k \frac{\partial^{2} ν^{(2)}}{\partial β^{2}} + (1 - k) \frac{\partial ν^{(2)}}{\partial β} = 0, β = 0, β = π .

Problem 3:

6

2 λ^{2} \frac{\partial^{4} ν^{(3)}}{\partial α^{2} \partial β^{2}} = \frac{q}{D} - f^{(1)} (α, β) - f^{(2)} (α, β) .

Conditions:

7

ν^{(1)} = ν^{(2)} = ν^{(3)} = ν,

needs to perform approximately. Let’s decompose RHS of Eqs. (4-6) to the Fourier series:

8

f^{(i)} (α, β) = \sum_{n = 1}^{\infty} \sum_{m = 1}^{\infty} a_{n m}^{(i)} s i n (n α) s i n (m β), (i = 1,2),

where $a_{n m}^{(i)}$ unknown constants, approximating unknown functions of the decomposition method.

Let’s decompose the load function $q$ to the Fourier series:

9

q (α, β) = \sum_{n = 1}^{\infty} \sum_{m = 1}^{\infty} q_{n m} s i n (n α) s i n (m β),

where $q_{n m}$ are coefficients of the load decomposition, and are determined using formula:

10

q_{n m} = \frac{4}{π^{2}} \int_{0}^{π} \int_{0}^{π} q (α, β) s i n (n α) s i n (m β) d α d β .

Then the auxiliary problems Eqs. (6-8) are written as follows.

Problem 1:

11

\frac{\partial^{4} ν^{(1)}}{\partial α^{4}} = \sum_{n = 1}^{\infty} \sum_{m = 1}^{\infty} a_{n m}^{(1)} s i n (n α) s i n (m β), ν^{(1)} = 0, π k \frac{\partial^{2} ν^{(1)}}{\partial α^{2}} + (1 - k) \frac{\partial ν^{(1)}}{\partial α} = 0,

α = 0, α = π .

Problem 2:

12

λ^{4} \frac{\partial^{4} ν^{(2)}}{\partial β^{4}} = \sum_{n = 1}^{\infty} \sum_{m = 1}^{\infty} a_{n m}^{(2)} s i n (n α) s i n (m β), ν^{(2)} = 0, π k \frac{\partial^{2} ν^{(2)}}{\partial β^{2}} + (1 - k) \frac{\partial ν^{(2)}}{\partial β} = 0,

β = 0, β = π .

Problem 3:

13

2 λ^{2} \frac{\partial^{4} ν^{(3)}}{\partial α^{2} \partial β^{2}} = \frac{1}{D} \sum_{n = 1}^{\infty} \sum_{m = 1}^{\infty} q_{n m} s i n (n α) s i n (m β)

- \sum_{n = 1}^{\infty} \sum_{m = 1}^{\infty} a_{n m}^{(1)} s i n (n α) s i n (m β) - \sum_{n = 1}^{\infty} \sum_{m = 1}^{\infty} a_{n m}^{(2)} s i n (n α) s i n (m β) .

And meeting the boundary conditions Eq. (11), we find:

14

ν^{(1)} = \sum_{n = 1}^{\infty} \sum_{m = 1}^{\infty} \frac{a_{n m}^{(1)}}{n^{3}} [\frac{1}{n} s i n (n α) + \frac{4 α^{3} k (k - 1)}{π^{2} (1 - 2 k - 11 k^{2})} + \frac{α^{2} (4 k - 5 k^{2} + 1)}{π (1 - 2 k - 11 k^{2})}

+ \frac{α (k^{2} - 1)}{(1 - 2 k - 11 k^{2})}] s i n (m β),

and solution of the boundary value problem Eq. (12) will be similar:

15

ν^{(2)} = \sum_{n = 1}^{\infty} \sum_{m = 1}^{\infty} \frac{a_{n m}^{(2)}}{λ^{4} m^{3}} [\frac{1}{m} s i n (m α) + \frac{4 β^{3} k (k - 1)}{π^{2} (1 - 2 k - 11 k^{2})} + \frac{β^{2} (4 k - 5 k^{2} + 1)}{π (1 - 2 k - 11 k^{2})}

+ \frac{β (k^{2} - 1)}{(1 - 2 k - 11 k^{2})}] s i n (n α),

where $a_{n m}^{(i)}$ bend surface decomposition coefficients to be determined. For this, the term of the series of $n$ , $m$ number for the load Eqs. (9) and the same term of the series of bend Eqs. (14-15). According to Eqs. (7) assume:

16

ν^{(3)} (\frac{π}{2}, \frac{π}{2}) = \frac{1}{2} [ν^{(1)} (\frac{π}{2}, \frac{π}{2}) + ν^{(2)} (\frac{π}{2}, \frac{π}{2})], ν^{(1)} (\frac{π}{2}, \frac{π}{2}) = ν^{(2)} (\frac{π}{2}, \frac{π}{2}) .

Now the problem is to determine individual terms of decomposition coefficients $a_{n m}^{(i)}$ from individual terms of load series Eq. (9). Then to determine $a_{n m}^{(i)}$ from Eq. (13) and Eq. (16) we will derive a system of algebraic equations. So, functions Eqs. (14-15) are the solution to the problem posed, since they meet the conditions on the plate contour and, when choosing the coefficients, derived by solving the system of algebraic equations. We introduce the notations:

3. Results and discussion

Fig. 1Computed plot of the coordinates α and β

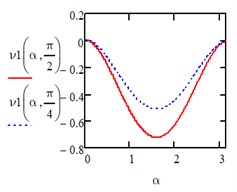
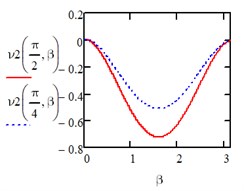
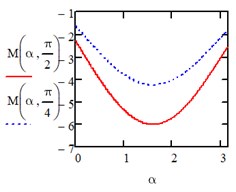
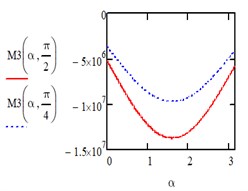
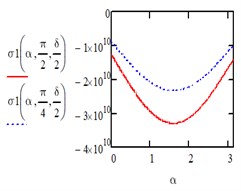
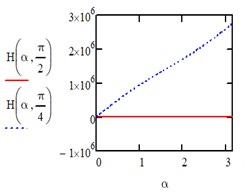
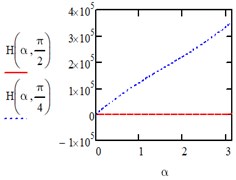
Under the action of a uniform load of the entire area we have:

G_{n m} = \frac{16 q}{D_{n m} π^{2}} s i n (\frac{n π}{2}) s i n (\frac{m π}{2}) .

Fig. 2Computed plot of the evenly distributed load

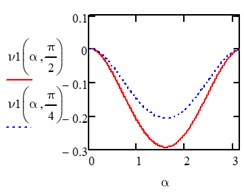
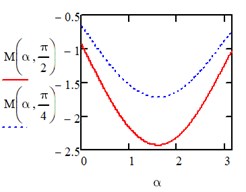
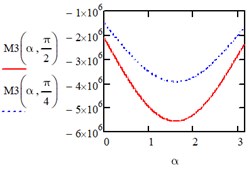
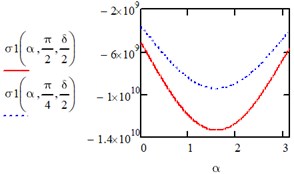
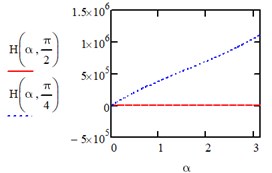
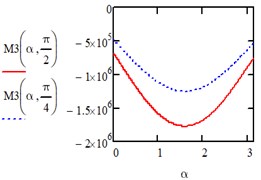
Under the action of a load changing along a parabola in the directions of the axis $α$ of the entire area we have:

G_{n m} = \frac{32 q}{D_{n m}^{3} π^{4}} [1 - {(- 1)}^{n}] s i n (\frac{n π}{2}) s i n (\frac{m π}{2}) .

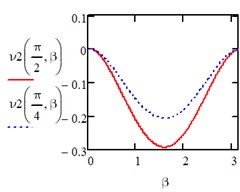
Fig. 3Computed plot of the changing parabola

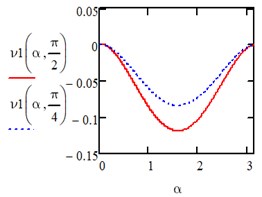
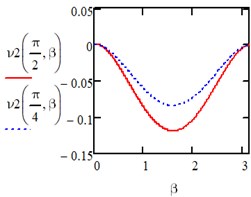
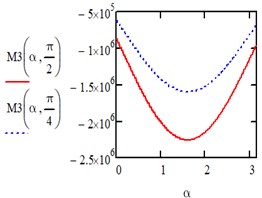
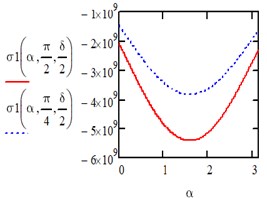
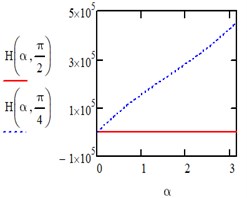
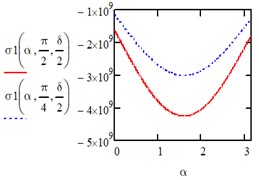
When the action is changing along an isosceles triangle in the directions of the axis $α$ of the entire area we have:

G_{n m} = \frac{16 q}{D_{n m}^{2} π^{3}} s i n^{2} (\frac{n π}{2}) s i n (\frac{m π}{2}) .

Fig. 4Computed plot of the isosceles triangle

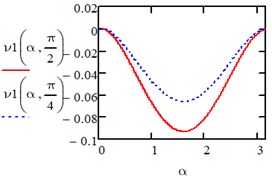
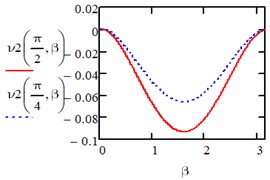
4. Conclusions

The paper obtained equations of plate bending, internal force factors and stresses, and the following new scientific results:

1) approximate analytical solutions were obtained for the functions of bends, the formulas of internal force factors and stresses given various boundary conditions of the plate and load;

2) the results of a numerical experiment for the plate were obtained given various fastenings of the edges and load;

3) mechanical effects, conditions of fastening along the contour and load were revealed.

References

Khairnasov K. Z. Mathematical modeling of dynamic stability of shell structures under large elastoplastic deformations. IOP Conference Series: Journal of Physics, Vol. 991, 2018, p. 012042.

Publisher
Omarov T., Tulegenova K., Bekenov Y., Abdraimova G., Zhauyt A., Ibadullayev M. Determination of reduced mass and stiffness of flexural vibrating cantilever beam. Journal of Measurements in Engineering, Vol. 6, Issue 1, 2018, p. 1-9.

Publisher
Mogilevich L. I., Popov V. S., Popova A. A., Christoforova A. V. Mathematical modeling of hydroelastic walls oscillations of the channel on Winkler foundation under vibrations. Vibroengineering Procedia, Vol. 8, 2016, p. 294-299.

Search CrossRef
Kondratov D. V., Kalinina A. V., Mogilevich L. I., Popova A. A., Kondratova Y. N. Mathematical model of elastic ribbed shill dynamics interaction with viscous liquid under vibrations. Vibroengineering Procedia, Vol. 8, 2016, p. 300-305.

Search CrossRef
Andreev V., Chepurnenko A. On the bending of a thin plate at nonlinear creep. Advanced Materials Research, Vol. 900, 2014, p. 707-710.

Publisher
Dickey R. W. Nonlinear bending of circular plates. Journal of Applied Mathematics, Vol. 30, Issue 1, 1976, p. 1-9.

Publisher
Reissner E. On the theory of bending of elastic plates. Journal of Mathematics and Physics, Vol. 23, 1944, p. 184-191.

Publisher
Charles Chinwuba Ike Mathematical solutions for the flexural analysis of Mindlin’s first order shear deformable circular plates. Mathematical Models in Engineering, Vol. 4, Issue 2, 2018, p. 50-72.

Publisher

Cited by

2021 IEEE International Symposium on the Physical and Failure Analysis of Integrated Circuits (IPFA)

(2021)

About this article

Received

20 February 2020

Accepted

26 May 2020

Published

26 November 2020

SUBJECTS

Mathematical models in engineering

DOI

https://doi.org/10.21595/vp.2020.21343

Erratum

The institutional affiliation was incorrect for Bidakhmet Zhanar in the paper finally approved (after the acceptance) by the authors. For more information read Editor's Note.

Keywords

mathematical modeling

high-strength

composite material

contour

solving problems

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 05 18

Uncertain optimization for composite base plate of mortar under impact load

Fengfeng Wang, Guolai Yang, Fengjie Xu

Research article

2020 11 26

Bending of a circular flexible plate taking into account the initial curvature

G. U. Mamatova, А. K. Sugirbekova, N. M. Bekaulov

Research article

2020 06 30

Effect of ply angle on nonlinear static aeroelasticity of high-aspect-ratio composite wing

Shuai Lei, Junli Wang, Tuolei Li, Wensheng Zhang, Zhigui Ren, Hong Cui

Research article

2018 03 31

Kantorovich variational method for the flexural analysis of CSCS Kirchhoff-Love plates

Charles Chinwuba Ike, Benjamin Okwudili Mama

S. Toibayev, A. Uderbayeva, Z. Bidakhmet, A. Rakhmatulina, and A. Zhauyt, “Mathematical modeling of the solution to the problem of plate bending given various fastenings along the contour and various loads,” Vibroengineering PROCEDIA, Vol. 35, pp. 52–57, Nov. 2020, https://doi.org/10.21595/vp.2020.21343

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2020.21343
UR  - https://doi.org/10.21595/vp.2020.21343
TI  - Mathematical modeling of the solution to the problem of plate bending given various fastenings along the contour and various loads
T2  - Vibroengineering PROCEDIA
AU  - Toibayev, Serikbay
AU  - Uderbayeva, Assemgul
AU  - Bidakhmet, Zhanar
AU  - Rakhmatulina, Ayaulym
AU  - Zhauyt, Algazy
PY  - 2020
DA  - 2020/11/26
PB  - JVE International Ltd.
SP  - 52-57
VL  - 35
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Toibayev_2020,
	doi = {10.21595/vp.2020.21343},
	url = {https://doi.org/10.21595/vp.2020.21343},
	year = 2020,
	month = {nov},
	publisher = {{JVE} International Ltd.},
	volume = {35},
	pages = {52--57},
	author = {Serikbay Toibayev and Assemgul Uderbayeva and Zhanar Bidakhmet and Ayaulym Rakhmatulina and Algazy Zhauyt},
	title = {Mathematical modeling of the solution to the problem of plate bending given various fastenings along the contour and various loads},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]S. Toibayev, A. Uderbayeva, Z. Bidakhmet, A. Rakhmatulina, and A. Zhauyt, “Mathematical modeling of the solution to the problem of plate bending given various fastenings along the contour and various loads,” Vibroengineering PROCEDIA, vol. 35, pp. 52–57, Nov. 2020, doi: 10.21595/vp.2020.21343.

Copy IEEE

Copied to clipboard!

Toibayev, Serikbay, Assemgul Uderbayeva, Zhanar Bidakhmet, Ayaulym Rakhmatulina, and Algazy Zhauyt. “Mathematical Modeling of the Solution to the Problem of Plate Bending given Various Fastenings along the Contour and Various Loads.” Vibroengineering PROCEDIA 35 (November 26, 2020): 52–57. https://doi.org/10.21595/vp.2020.21343.

Copy Chicago

Copied to clipboard!

Mathematical modeling of the solution to the problem of plate bending given various fastenings along the contour and various loads

Abstract

1. Introduction

2. Materials and methods

3. Results and discussion

4. Conclusions

References

Cited by

About this article

Related Articles