Inherent characteristic analysis of a precast concrete vibrating table based on the Rayleigh-Ritz method

1. Introduction

As a key component of prefabricated buildings, precast concrete is gradually being utilized in larger sizes and more complex shapes. Producing precast concrete with high efficiency and high quality has become an important research area. In particular, precast concrete vibrating tables are used as major molding tools in the production of precast concrete. As a result, the vibration characteristics analysis and structural optimization design of precast concrete vibrating tables have important applications and value. However, in practical operation, once the excitation frequency is close to the natural frequency of the vibration platen, the resonance can cause damage to the equipment [1-3]. To avoid resonance, it is necessary to analyze the inherent characteristics of the vibration platens, which is the theoretical basis for improving the performance of vibrating tables; this provides guiding significance for the theoretical analysis and the optimized design of equipment for the improvement of precast concrete [4-7].

Recently, scholars have performed research on the inherent characteristics of vibrating tables. Zhao et al. [8] analyzed the vibration characteristics of a 3-P(4S) parallel vibrating table and solved the vibration equation of the system to obtain the natural frequency and mode shapes of the mechanism. ADAMS vibration simulations and modal experiments were combined to verify the correctness of the inherent characteristics by theoretical analysis. Wang et al. [9] used finite element software to solve the natural frequency and mode shapes of vibrating tables for product packaging vibration tests and optimized the structure of the vibrating table to improve the natural frequency and avoid resonance.

The analysis of complex structures with stiffeners, such as vibrating tables and bridge decks, they can be abstracted into stiffened plate structures with equivalent mechanical behavior using structural similarity [10]. Many domestic and foreign scholars have performed research on stiffened plates. Ma et al. [11] studied the nonlinear vibration characteristics of stiffened plates and divided the stiffened plates into two parts: plates and stiffeners. Then, the vibration differential equation of the stiffened plates was derived using the Lagrange equation and modal superposition method under the assumption of stiffened plate displacement. Finally, four-sided fixed stiffened plates under simple harmonic excitation were studied using a multiscale method. The first-order approximation solutions of the system’s double motion were obtained, and the nonlinear forced vibration characteristics of stiffened plates were obtained to provide a theoretical basis for engineering design. Ahmad et al. [12] analyzed stiffened plates using the first-order shear deformation theory and solved the vibration differential equation of stiffened plates using the Rayleigh-Ritz method and then proposed using the analytical integral of integrands to replace the recursive integral in the loop structure of computer programs. The calculation efficiency was greatly improved. Additionally, a comparison between the numerical calculation results and ABAQUS simulation results showed that the accuracy of the numerical calculation was higher than that of the traditional algorithm. You et al. [13] analyzed the free vibration problem of stiffened plates by using an edge-based smoothed finite element method and obtained the natural frequency of a four-sided simply supported stiffened plate. The results showed that using strain-smoothing technology can effectively reduce the stiffness of the finite element model and thus obtain a smooth finite element model closer to the actual stiffness, and the edge-based smoothed element method has higher calculation accuracy than the traditional finite element method.

In this paper, based on the transverse vibration theory of thin plates, the vibration platen was simplified as a stiffened plate structure according to the current structural characteristics of the vibration platen. Then, a mechanical model of the vibrating table was established, and the inherent characteristics of the vibrating table were analyzed. This provided theoretical guidance for the performance improvement of vibrating tables and the optimized design of vibrating table equipment. The novelty of this study is that the flexural vibration theory of elastic rectangular plates is used in the analysis of the vibration table. Additionally, the optimization of mathematical model is made, according to the structural characteristics of the vibration table, when the inherent characteristics of the vibration table are solved.

2. Mechanical model of precast concrete vibrating table

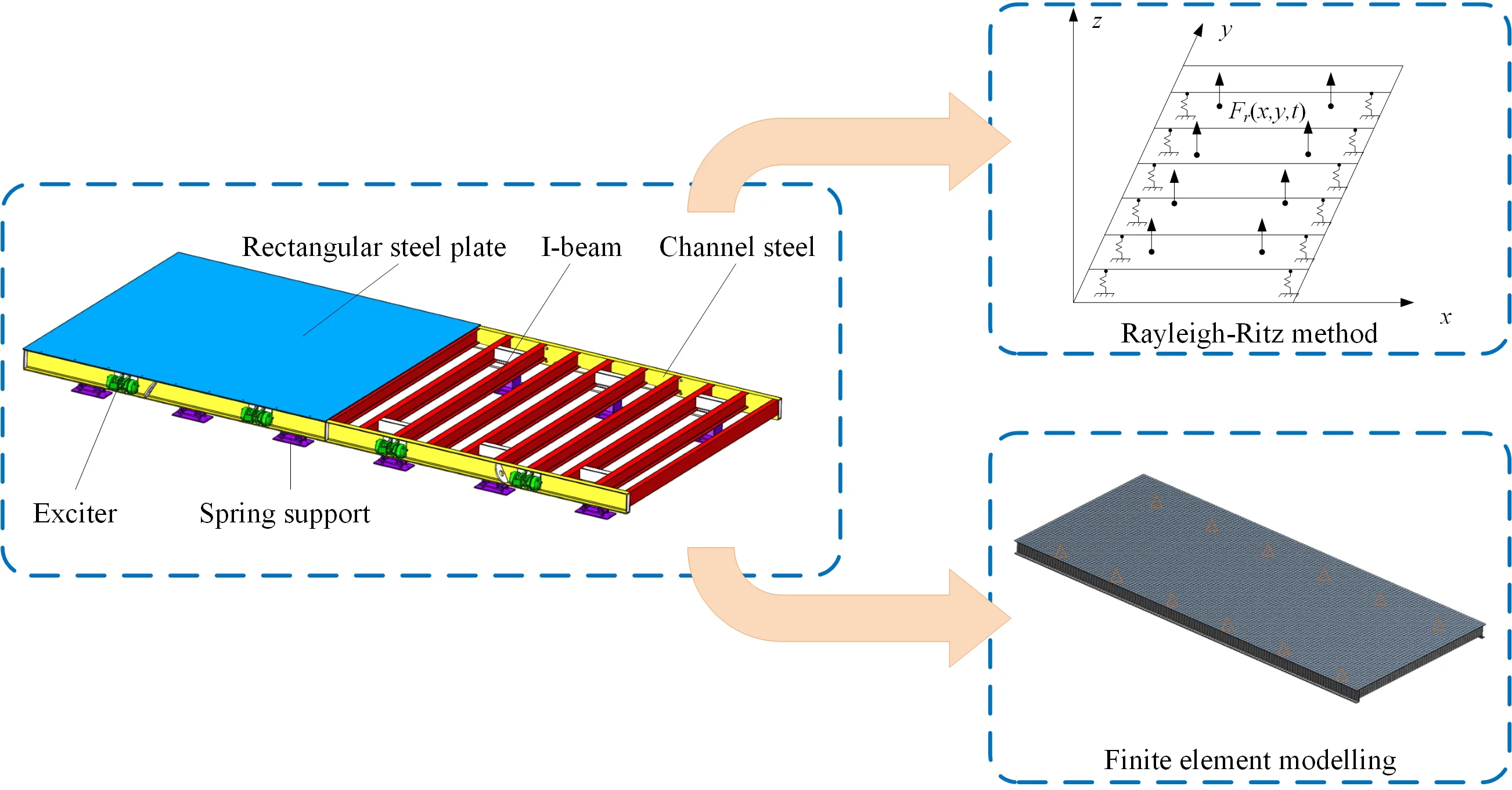
A precast concrete vibrating table system is mainly composed of a vibration platen, spring supports and exciters. The vibration platen is a welded component consisting of a rectangular steel plate and section steel (both I-beam steel and channel steel). Twelve rubber springs are distributed at the bottom of the vibration platen for support and reduced vibration. Each channel steel web is installed with 4 vibration exciters to provide an exciting force so that the precast concrete on the vibrating table is densely formed. The structure of the precast concrete vibrating table system is shown in Fig. 1.

Fig. 1Schematic of precast concrete vibrating table system structure

In addition, a lot of studies about spring supports have been done. Demetriades et al. [14] investigated the advantages of wire rope isolators (WRIs) in the seismic protection of buildings. Different and more accurate mathematical models were proposed by Leblouba et al. [15] as well as Vaiana et al. [16] to represent the realistic mechanical behaviors of WRIs under axial compressive force. Fiber-reinforced elastomeric isolators were proposed by Losanno et al. [17] and Madera et al. [18]. This isolator, which is more effective and inexpensive, is used in the base isolation system of low-rise buildings in Colombia. Vaian et al. [19] used a uniaxial phenomenological model to solve the isolator restoring force. Compared to the classic model, the proposed model improved the numerical accuracy and computational efficiency.

According to the actual working conditions, the following assumptions are made when establishing the precast concrete vibrating table mechanical model.

(1) The model is equivalent to a stiffened plate structure according to the structural characteristics of the vibration platen. It can be regarded as a thin plate since the thickness of the rectangular steel plate is much smaller than the length and width of the rectangular steel plate, and the section steel is analyzed as a Euler-Bernoulli beam.

(2) Since the support area of the rubber spring is much smaller than the area of the vibration platen, it is regarded as an elastic point support.

(3) The vibration exciter excites the vibration platen as a concentrated dynamic load.

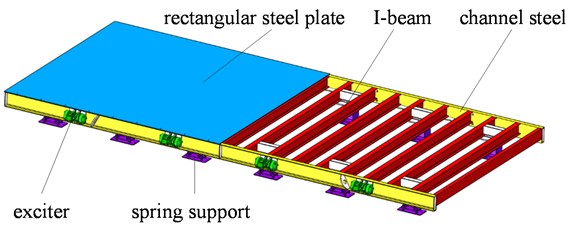
Based on the above assumptions, the analysis of vibration platen inherent characteristics can be transformed into a “free vibration problem of stiffened plates with multiple elastic point supports”. The mechanical model of the precast concrete vibrating table is shown in Fig. 2.

Fig. 2Mechanical model of precast concrete vibrating table

According to the actual state of the precast concrete vibrating table, the boundary conditions of the vibration platen are free on four sides, and the bending moments and shear forces at all points on the edges are zero:

where $w=w\left(x,y,t\right)$ is the deflection function of the vibration platen and $\nu$ is the Poisson’s ratio of the rectangular plate steel.

According to Hooke’s law, the shear force and deflection of the vibration platen at the spring support have the following relationship:

where $k_s$ is the stiffness of the $s$-th rubber spring and $\left(x_s,y_s\right)$ is the position coordinate of the $s$-th support point.

In summary, the natural characteristics analysis of the vibration platen analyzes the natural vibration of the vibration platen under boundary conditions Eq. (1) and support conditions Eq. (2). Due to the complexity of actual engineering situations, it is difficult to directly obtain an accurate solution, and the approximate solution has the advantages of simplicity, small relative error, etc. This paper uses the Rayleigh-Ritz method that based on the variational principle of displacement.

3. Analysis of inherent characteristics of vibration platen

3.1. Theoretical modeling

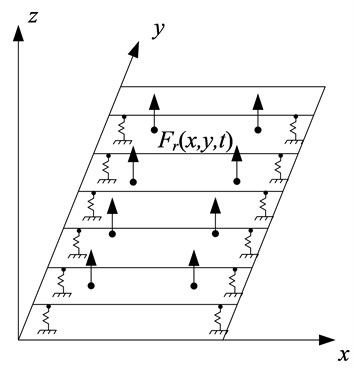
The vibration platen of the precast concrete vibrating table studied in this paper consists of a rectangular steel plate with a width $a$, a length $b$ and a thickness $h$ along with a section steel frame. Because section steel has the advantages of high rigidity and light weight, it can ensure that the vibration platen has a large increase in stiffness with a small increase in mass so that the equipment can run smoothly, reduce noise, and improve energy efficiency. The theoretical model of precast concrete vibrating table is shown in Fig. 3 and main parameters are summarized in Table 1.

Fig. 3Theoretical model of vibration platen

Table 1Main dimension parameters of the vibration platen

Parameter name		Parameter value
Plate	Length / m	9
	Width / m	4
	Thickness / m	0.01
I beam	Model	20a
	Length / m	3.8
Channel steel	Model	28c
	Length / m	8.98

The $x$-$y$ coordinate system is established with the middle surface of the rectangular steel plate as a reference surface. According to the classic theory of thin plates [20], the displacement field of rectangular steel plates can be expressed as:

3

$\left\{\begin{array}{c}u\left(x,y,z,t\right)=u_0\left(x,y,t\right)-z\frac{\partial w}{\partial x},\\ v\left(x,y,z,t\right)=v_0\left(x,y,t\right)-z\frac{\partial w}{\partial y},\\ w\left(x,y,z,t\right)=w\left(x,y,t\right),\end{array}\right.$

where $u_0\left(x,y,t\right)$, $v_0\left(x,y,t\right)$, and $w\left(x,y,t\right)$ are the mid-plane displacements of the rectangular steel plate in the$x$, $y$, and $z$ directions, respectively.

The main motion form of the rectangular steel plate is transverse vibration perpendicular to the mid-plane of the rectangular steel plate according to the actual working condition of the precast concrete vibrating table equipment [21]. Therefore, the transverse vibration of rectangular steel plates is mainly considered; that is, the mid-plane displacement $u_0$ and $v_0$ are ignored. According to the theory of thin plates, the strain component at any point in the rectangular steel plate is:

4

$\left\{\begin{array}{c}{\epsilon }_x=\frac{\partial u}{\partial x}=-z\frac{{\partial }^{2}w}{\partial x^2},\\ {\epsilon }_y=\frac{\partial v}{\partial y}=-z\frac{{\partial }^{2}w}{\partial y^2},\\ {\gamma }_{xy}=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=-2z\frac{{\partial }^{2}w}{\partial x\partial y}.\end{array}\right.$

The rectangular steel plate and section steel have a consistent displacement according to the deformation coordination. Due to the structural characteristics of section steel, each section mainly considers the positive strain caused by bending, and the strain of the $i$-th section steel along the $x$ and $y$ directions is:

5

$\left\{\begin{array}{c}{\epsilon }_{xi}=-z\frac{{\partial }^{2}w}{\partial x^2},\\ {\epsilon }_{yi}=-z\frac{{\partial }^{2}w}{\partial y^2}.\end{array}\right.$

It can be seen that the expressions of ${\epsilon }_{xi}$ and ${\epsilon }_{yi}$ in Eq. (5) are the same as the expressions of ${\epsilon }_x$ and ${\epsilon }_y$ in Eq. (4). Calculating the strain of the section steel according to Eqs. (4) and (5) can satisfy the deformation coordination between the section steel and the rectangular steel plate.

When the vibration platen is analyzed by the Rayleigh-Ritz method, the deformation energy and kinetic energy of the section steel are added to the energy of the rectangular steel plate, and the solution of the displacement function of the section steel is approximate to the analytical solution of the rectangular steel plate [22]. The total energy of the vibration platen system is the energy sum of the rectangular steel plate and section steel, and the elastic strain energy at each support point needs to be considered. For the theoretical model of the vibration platen that is established in Fig. 3, there are $N_x$ I-beams parallel to the $x$-axis and $N_y$ channel steels parallel to the $y$-axis. According to the strain relationship Eq. (4) and the assumptions in Section 2, the strain energy $U$ and kinetic energy $T$ of the system can be expressed as:

6

$U={\int }_0^b{\int }_0^a\frac{D}{2}\left\{{\left(\frac{{\partial }^{2}w}{\partial x^2}+\frac{{\partial }^{2}w}{\partial y^2}\right)}^2-2\left(1-\nu \right)\left[\frac{{\partial }^{2}w}{\partial x^2}\frac{{\partial }^{2}w}{\partial y^2}-{\left(\frac{{\partial }^{2}w}{\partial x\partial y}\right)}^2\right]\right\}dxdy$
$=+\sum _{i=1}^{N_x}{\int }_0^a\frac{E_x{I}_x}{2}{\left(\frac{{\partial }^{2}w}{\partial x^2}\right)}_{y=y_i}^{2}dx+\sum _{i=1}^{N_y}{\int }_0^b\frac{E_y{I}_y}{2}{\left(\frac{{\partial }^{2}w}{\partial y^2}\right)}_{x=x_i}^{2}dy+\sum _{s=1}^{12}\frac{1}{2}{k}_s{w}^2\left(x_s,y_s\right),$

and:

7

$T={\int }_0^b{\int }_0^a\frac{\rho h}{2}{\left(\frac{\partial w}{\partial t}\right)}^{2}dxdy+\sum _{i=1}^{N_x}{\int }_0^a\frac{{\rho }_x{A}_x}{2}{\left(\frac{\partial w}{\partial t}\right)}_{y=y_i}^{2}dx+\sum _{i=1}^{N_y}{\int }_0^b\frac{{\rho }_y{A}_y}{2}{\left(\frac{\partial w}{\partial t}\right)}_{x=x_i}^{2}dy,$

where:

$D=\frac{E{h}^3}{12(1-{\nu }^2)},$

where $D$, $E$, $\rho$, $h$, and $\nu$ are the bending stiffness, elastic modulus, density, thickness, and Poisson’s ratio of the rectangular plate steel, respectively.

$E_x$, $I_x$, ${\rho }_x$, $A_x$ and $E_y$, $I_y$, ${\rho }_y$, $A_y$ are the elastic modulus, moment of inertia, density, and cross-sectional area of the section steel in the $x$ and $y$ directions, respectively.

4. Verification of theoretical calculation

A comparison method between the calculation results and the finite element simulation results is adopted to verify the correctness of the theoretical analysis method and the calculation results of vibrating platen inherent characteristics.

First, the finite element model of the vibrating platen was established according to the size parameters in Table 1. The rectangular steel plate and section steel materials were Q235, and the main material parameters were an elastic modulus $E$ = 2.06×10¹¹ Pa, a Poisson’s ratio $\nu$ = 0.3, and a density $\rho =$ 7850 kg/m³. The rectangular steel plate was simulated by shell elements, and the section steel was simulated by solid elements. Then, meshing is performed and constraints are applied according to the actual working state of the precast concrete vibrating table. The specific constraints are as follows: constrain the translational degrees of freedom along the $x$-axis and $y$-axis and the rotational degrees of freedom around the $z$-axis of the vibrating platen, and apply elastic support at the support points on the bottom of the vibration platen to simulate the rubber spring seat. Finally, the natural frequencies and mode shapes of the vibrating platen are solved. The finite element model of the vibration platen has a total of 35863 units and 169545 nodes. Fig. 4 and Fig. 5 show the finite element models of the vibration platen and section steel, which were established by the finite element software ANSYS Workbench.

Fig. 4Finite element model of the vibration platen

Fig. 5Finite element model of the section steel

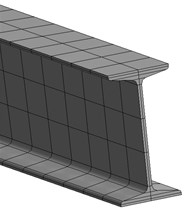
a) Finite element model of I-beam

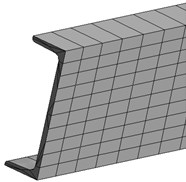
b) Finite element model of channel steel

Fig. 6Vibration platen mode shape comparison between theoretical calculation (left) and simulation analysis (right)

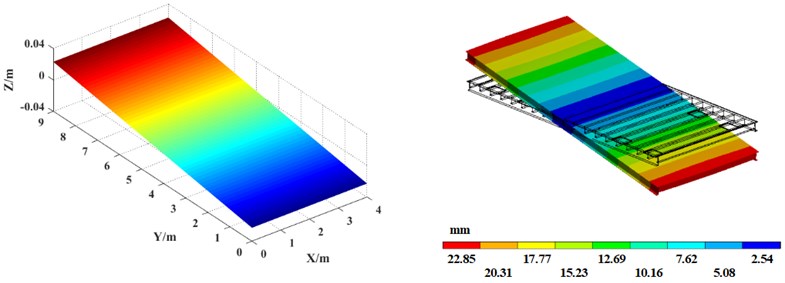
a) 1st mode shape

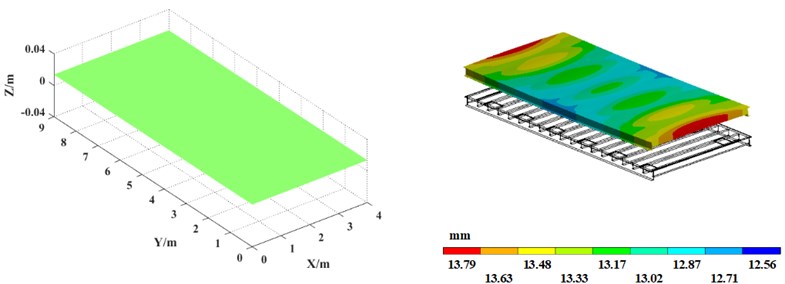
b) 2nd mode shape

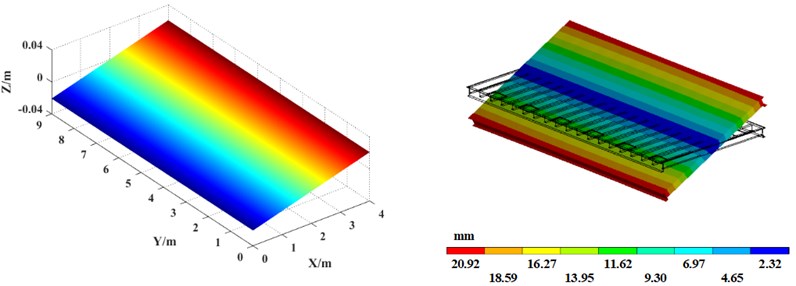
c) 3rd mode shape

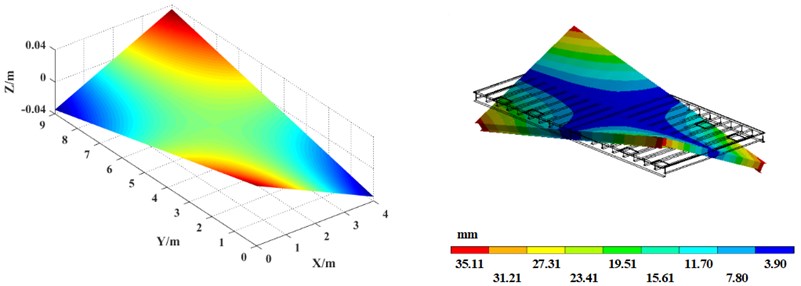
d) 4th mode shape

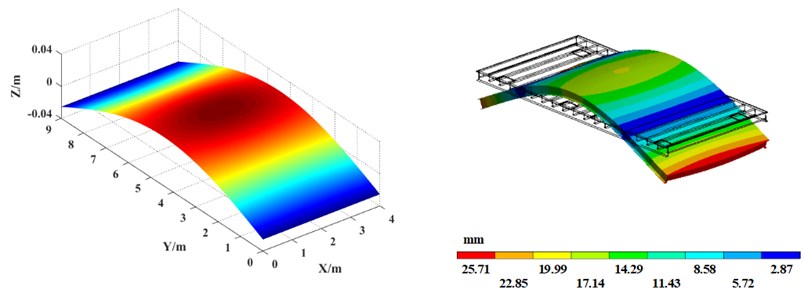
e) 5th mode shape

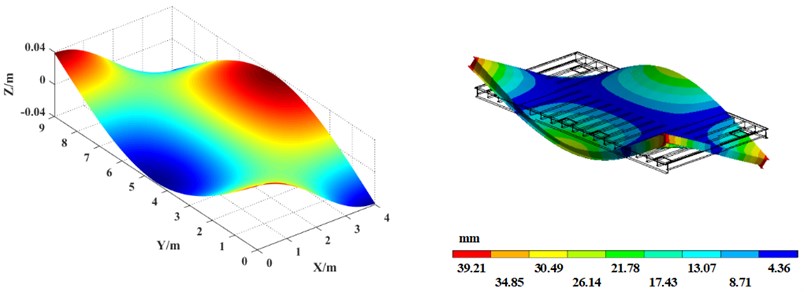
f) 6th mode shape

Table 3 shows the first 10th-order natural frequency of the vibrating platen obtained by finite element software. For comparison, the theoretical calculation results obtained by the MATLAB program are also listed in Table 3. In addition, the comparison of the first 6th-order mode shapes of the vibration platen obtained by the simulation analysis and theoretical calculation is shown in Fig. 6.

The comparison shows that the error between the theoretical calculation result and the finite element simulation result of the natural frequency of the vibrating table ranges between 0.30 %-3.15 %, and the error is within the allowable range. Additionally, the theoretically calculated modal shapes agree well with those of the simulation analysis, verifying the correctness of the theoretical calculation. The results of this paper can guide the reasonable selection of vibration frequency when the precast concrete vibrating table is working, effectively avoiding the natural frequency of the vibration platen and preventing resonance. In addition, using the theoretical analysis method in this paper can evaluate the inherent characteristics of vibration platens with different section steel layouts, realize the optimal structural design of vibrating platens, improve the vibration effect of precast concrete vibrating tables, and improve the quality of prefabricated components.

5. Conclusions

1) Based on the transverse vibration theory of thin plates, a mechanical model of a precast concrete vibrating table system was established, and the vibration mode function of the vibration platen was constructed by a two-dimensional beam function method. The maximum strain energy and the maximum kinetic energy of the vibration platen were derived by considering the strengthening of the section steel. Using the Rayleigh-Ritz energy method, the natural frequency and mode shapes of the vibration platen were obtained, thus providing a theoretical analysis method for the inherent characteristic analysis of a precast concrete vibrating table.

2) Taking a certain type of vibration platen as the study object, a MATLAB program was written to solve the inherent characteristics of the vibration platen. The natural frequency and mode shape obtained by theoretical calculations were compared with the results of finite element analysis. The results showed that the theoretical calculation results were consistent with the finite element analysis results, and the correctness of the theoretical analysis method for the inherent characteristics of vibrating platens was verified.

3) The analysis results of the inherent characteristics of vibration plates can furnish reference data for existing precast concrete vibrating tables to avoid resonance, provide a theoretical basis for the structural optimization and performance improvement of the same type of precast concrete vibrating table system, and effectively improve the quality of precast concrete forming.

4) There is a limitation in this study. Specifically, the spring supports were modeled as linear elastic elements. However, the actual behavior of these devices is typically nonlinear and there are more sophisticated methods that are generally utilized to simulate their responses [23-25]. We will use these methods in future research.