Design and analysis of actuator system of electromagnetic shell with high-overload resistances

2.1. Electric actuator system of electromagnetic shell

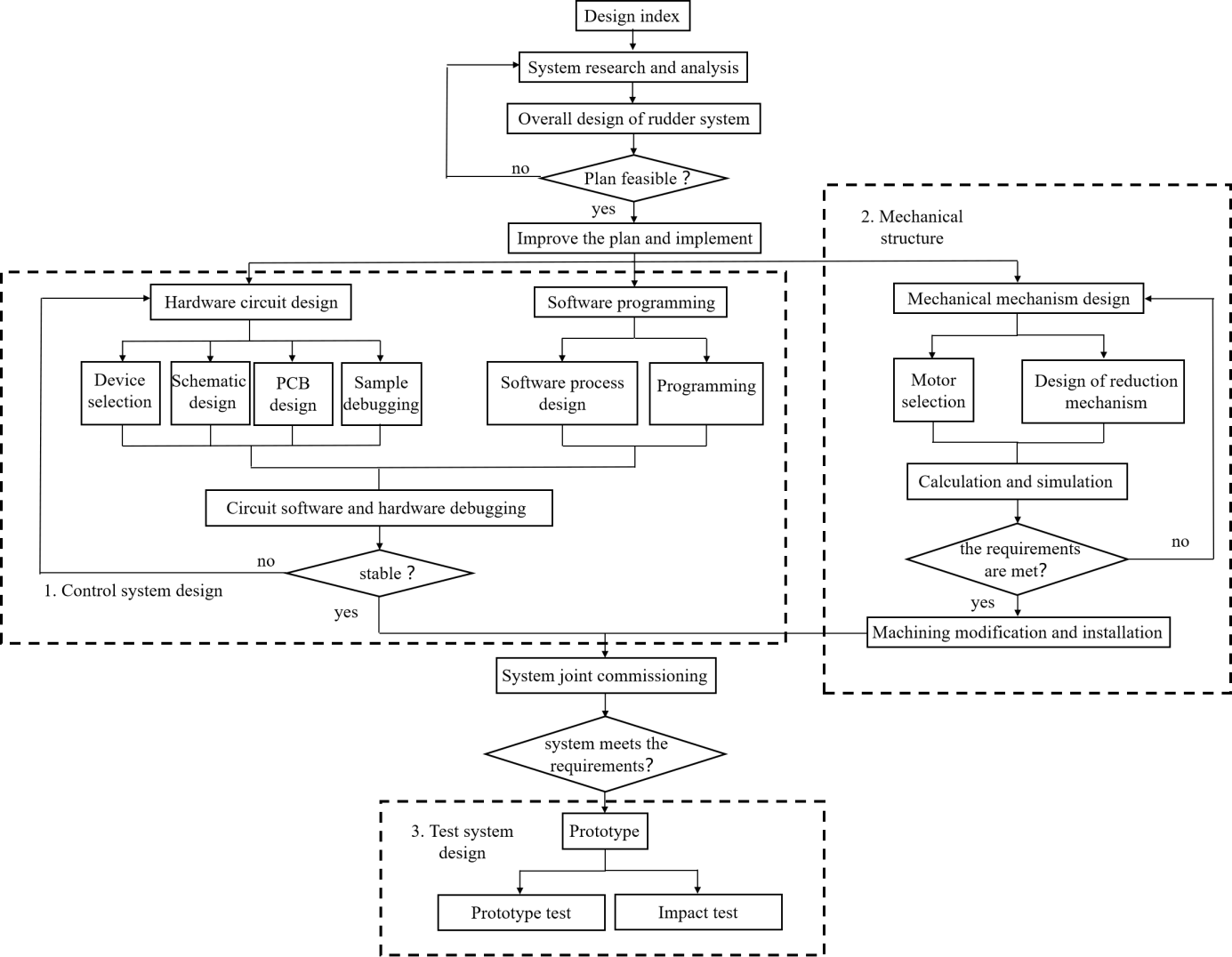
The steering gear is the main part of the direction control system of electromagnetic projectiles. It enables the rudder of the electromagnetic shell to track and locate accurately according to the given speed and motion track. When the motor acquires enough energy to drive the rudder blade deflection, the deviation between the input and feedback output is minimized. The steering system is generally composed of five parts: controller circuit, driver circuit, servo motor, reducer, and feedback potentiometer. According to the integrated module method of complex mechanical and electrical equipment, the design of the new high-overload electromagnetic shell steering gear system is divided into the control system, mechanical structure, and test system design parts. The overall design strategy of the new high-overload electromagnetic shell steering system is shown in Fig. 1. Table 2 shows the performance requirements of the new electromagnetic shell actuator designed in this study.

Fig. 1The overall design strategy of new high overload electromagnetic shell steering system

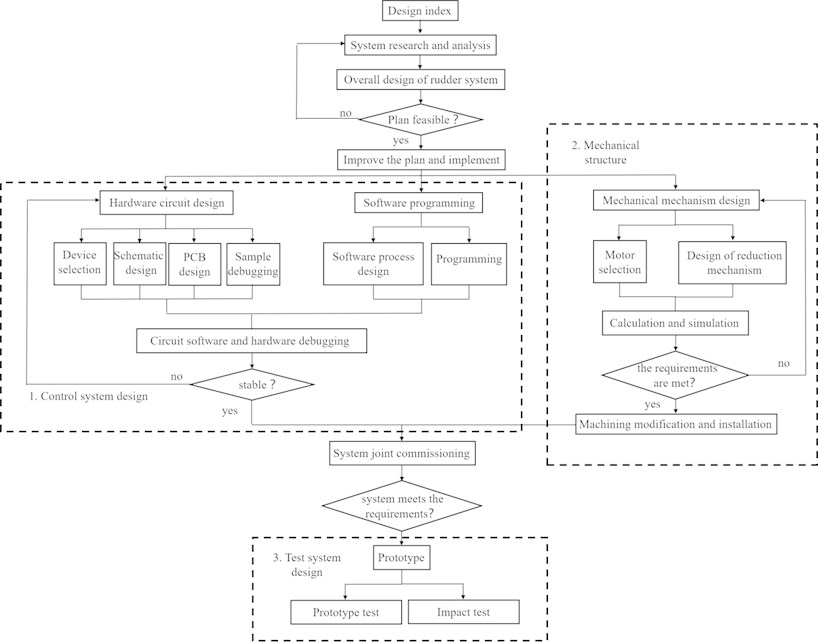
2.2. Design and principle of control system for electric actuator of high-overload electromagnetic shell

A schematic diagram of the electric actuator control system of the high-overload electromagnetic shell is shown in Fig. 2. The system primarily comprises a gear body and a driver. The steering gear body consists of a DC motor, reducer, and feedback potentiometer. The dotted line in Fig. 2 denotes the actuator, which is composed of the main control circuit, isolation amplifier circuit, and drive circuit. In this study, PID control was adopted as the control strategy for the electromagnetic shell electric actuator.

2.3. High-overload structure design of new electromagnetic shell electric actuator

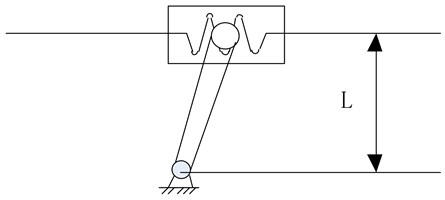
Because of the small volume of the electric rudder cabin of the electromagnetic shell, the rolling screw drive structure was selected in this study. As shown in Fig. 3, to meet the performance requirements of the steering gear, a new deceleration mechanism combining a triangular screw and a fork was developed to resist high overloads. According to the performance index requirements listed in Table 1, the rated output torque and speed of the motor were 30 N∙mm and 5000 rpm, respectively. When the rudder was unloaded, the maximum deflection speed of the rudder blade exceeded 190 °/s, which is equivalent to 31.67 rpm. The total deceleration ratio satisfies Eq. (1):

In Eq. (2), $P$ is the lead of the screw, and L is the distance from the rudder axis to the lead screw axis. The positions of rudder shaft and screw axis are shown in Fig. 3. The transmission ratio of the triangular screw is expressed as Eq. (3).

Fig. 2The control block diagram of high overload electromagnetic shell electric actuator

Fig. 3location of rudder shaft and lead screw axis

In this study, the pitch was set as 1. The length of the transmission lead screw and shift fork swing arm was set as 13.6. The reduction ratio of the transmission system was 85. Under the rated condition, the maximum torque and the maximum angular velocity of the rudder blade deflection were calculated using Eq. (3) and Eq. (4), respectively:

According to the calculation results of Eq. (3) and Eq. (4), the reduction ratio of motor and triangular screw met the design requirements. The electric actuator structure of the proposed anti-high load electromagnetic shell is presented in Fig. 4.

3.1. Modal analysis of steering gear system of electromagnetic projectile with high-overload resistance

Modal analysis is a type of fundamental linear dynamic analysis and is widely used to determine the vibration characteristics of mechanical structures. It can be used to avoid resonance in the early stages of mechanical structure design or induce vibrations at a specific frequency. Vibration characteristics are an important parameter to verify the reliability and stability of structural design under dynamic loads. The vibration model of the system is shown in Eq. (5):

where, $K$ – stiffness matrix of the system, $M$ – quality matrix of system, $F\left(t\right)$ – external force matrix of the system, $F\left(t\right)$ equals 0 in Eq. (5):

Fig. 4Structure of electric actuator of new anti high load electromagnetic shell

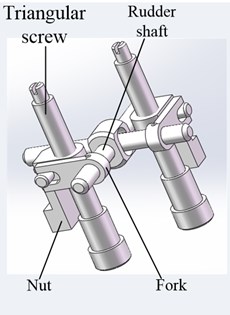
a) High overload transmission structure

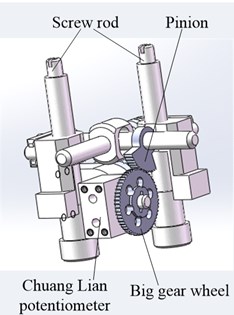
b) Angle feedback structure

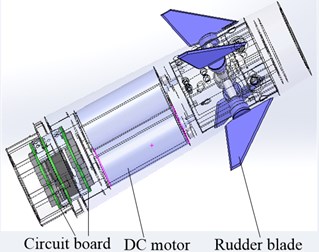
c) Electric actuator structure

Eq. (6) is taken into Eq. (5), then a second equation is shown in Eq. (7):

In Eq. (7), $x=A\mathrm{s}\mathrm{i}\mathrm{n}(\omega t-\phi )$:

By solving the determinant equation $\left|K-{\omega }^{2}M\right|=0$, where ${\omega }_i^2$ is the natural frequency of the order $i$, the main mode shape, $A_i$, of the $i$th natural frequency could be obtained. The simplified anti-high-overload electromagnetic shell actuator system model was imported into ANSYS and assigned materials. The main material of electromagnetic shell electric actuator was 40 Cr, and the material properties are shown in Table 2.

The steering system model of the electromagnetic projectile against high overload was meshed. To balance the trade-off between computing time and meshing accuracy, the mesh size of this model was controlled at 3 mm. To maximize meshing quality, the hexahedron and tetrahedron integrated division method was adopted. Consequently, 265435 nodes and 148023 units were obtained, and the integrated meshing quality was 0.72, as shown in Fig. 5(a) and (b). The motor and the high-strength screws between the potentiometer and the cylinder wall were fixedly connected. The modal simulation of the steering gear was performed in a free state. The first six rigid body displacement modes were discarded. The first eight natural frequencies obtained from the modal analysis are shown in Table 3.

Fig. 5Meshing of steering gear system

a) Meshing model

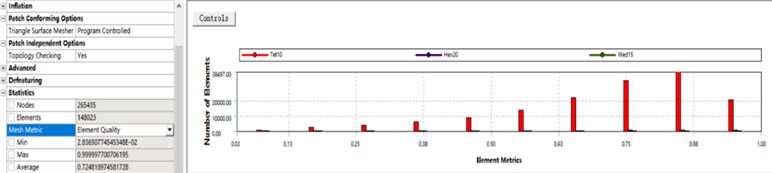
b) Meshing quality

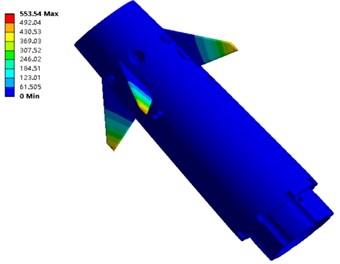
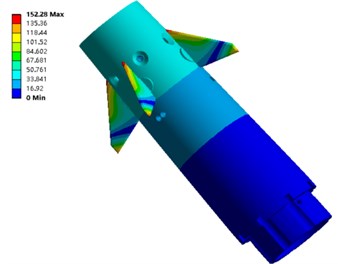
The first eight vibration modes are shown in Fig. 6. It should be noted that the maximum vibration position of the fourth and eighth order modal inside the electromagnetic shell. In the figure, to clearly display the internal vibration modes of the steering gear system of the anti-high-overload electromagnetic shell, the cylinder wall is hidden.

Observe the deformation of the first six modes to know the vibration form of each mode, as shown in Table 4.

According to the above finite element calculation, the accuracy of the model needs to be verified using a free mode test. In this paper, the B & K modal test system was used. The test setup is shown in Fig. 7, which mainly includes an acceleration sensor and force hammer. During the free mode test, the rudder of the electromagnetic shell was suspended using an elastic rope. This modal test adopted the multi-point excitation single point response method. The acceleration sensor was fixed at one measuring point, and the moving hammer was used to knock each measuring point. To obtain accurate test results, 18 test points were marked on the surface of the tested piece, and each measuring point was knocked five times, and the measurements were averaged to eliminate random error. Then, each datum was recorded.

Fig. 6The first eight modes of the steering system model of anti-high overload electromagnetic shell

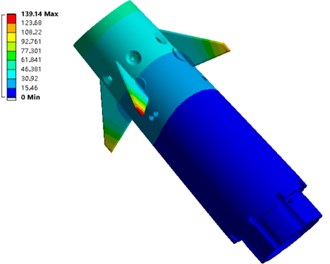
a) Vibration mode of first order

b) Vibration mode of second order

c) Vibration mode of third order

d) Vibration mode of fourth order

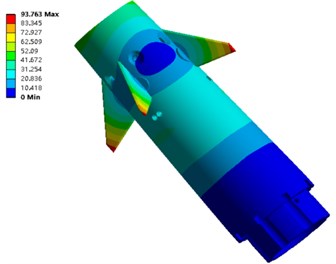
e) Vibration mode of fifth order

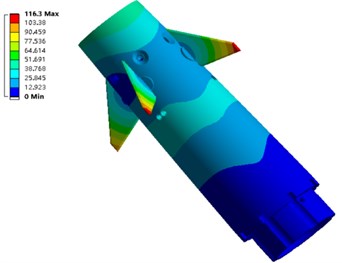
f) Vibration mode of sixth order

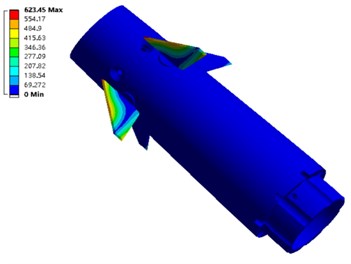
g) Vibration mode of seventh order

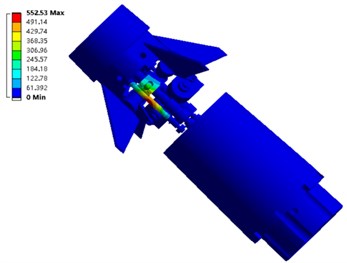
h) Vibration mode of eighth order

Fig. 7Modal test of electromagnetic shell steering gear

Table 5 shows a comparison between the test modal frequency and finite element calculation results. It was found that the maximum error between the first eight natural mode frequencies obtained experimentally and via the finite element calculation was 6.6 %, and that for the remaining modes was less than 5 %, which is acceptable in engineering applications. The above analysis validated the proposed electromagnetic shell.

3.2. Transient dynamic analysis of actuator system of electromagnetic projectile with high-overload resistance

A transient dynamic analysis was performed to determine the dynamic response of a structure under arbitrary time-varying loads. Particularly, the displacement, strain, and stress of the system structure under a random combination of steady-state load, transient load, and simple harmonic load were determined. These are important indexes to evaluate the anti-high-overload performance of the system structure. The basic motion equation of the system is shown in Eq. (9):

where $\left[M\right]$ is mass matrix, $\left[C\right]$ is damping matrix, $\left[K\right]$ is stiffness matrix, $\left\{\ddot{u}\right\}$ is node acceleration vector, $\left\{\dot{u}\right\}$ is node velocity vector, $\left\{u\right\}$ is node displacement vector.

At any instant, Eq. (5) can be regarded as a series of mechanical balance equations considering inertia force $\left[M\right]\left\{\ddot{u}\right\}$ and damping force $\left[C\right]\left\{\dot{u}\right\}$. The time increment integration time step is initialized, and the New-mark time integration method is used to solve this equation at discrete time points.

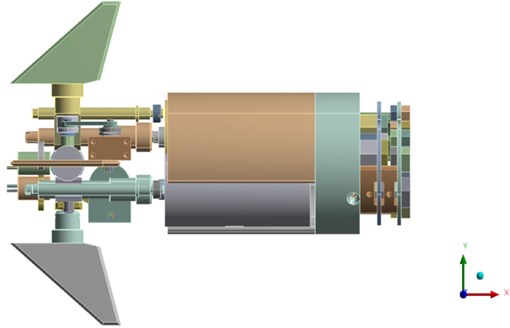
According to the requirements of technical indicators, the electric actuator of the electromagnetic shell should meet the high-overload requirements of an axial overload of 120000 N and a transverse overload of 40000 N. To facilitate the application of the impact load to the model, the three-dimensional coordinates of the model were first set, as shown in Fig. 8. Then, the horizontal direction parallel to the motor axis on the right was set as the positive longitudinal $x$-axis direction, vertical to the motor axis to the up as the transverse $y$-axis positive direction, and vertical to the motor axis. The positive vertical $z$-axis direction was set in the direction of the motor shaft and was horizontally outward.

Fig. 8Three dimensional coordinates setting of anti high overload electromagnetic shell steering gear system

3.2.1. Longitudinal transient impact analysis

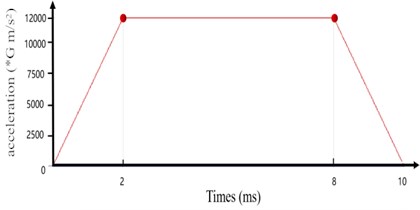
A longitudinal (positive $x$ axis) transient impact acceleration of 12000 g was applied to the actuator system model of the electromagnetic projectile, and the high-strength screws between the motor and potentiometer and the cylinder wall were fixedly connected. The eight bolt holes of the cylinder wall were fully constrained. Because the acceleration time of electromagnetic projectiles in electromagnetic orbit is generally short, the impact time was set as 10 ms. During this time, the projectile rises for 2 ms, stays in orbit for 6 ms, and falls for 2 ms. Fig. 9(a) and (b) show the longitudinal transient impact analysis boundary conditions and diagram of the longitudinal transient impact time load, respectively.

Fig. 9a) Longitudinal transient impact analysis boundary conditions; b) time load diagram of longitudinal transient impact

a)

b)

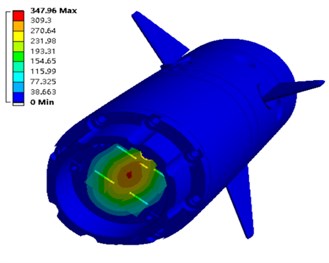
The analysis results are shown in Fig. 10 and Fig. 11. Fig. 10 shows the dynamic characteristic curve of the maximum deformation and maximum equivalent stress of the actuator system model of the electromagnetic shell under the longitudinal transient impact load. At 0-2 ms, the system responds rapidly, and its maximum deformation and maximum equivalent force increase rapidly (0.013 mm for total deformation and approximately 103 MPa for equivalent stress). Subsequently, these parameters remain stable until 8 ms, when the 12000 g transient impact load is removed. Thereafter, the values of these two parameters decline until the load is removed at 10 ms. The deformation and equivalent stress are reduced to 1.63e-4 mm and 1.12 MPa, respectively.

Between 2 ms and 8 ms, the maximum deformation and equivalent stress only fluctuate slightly and maintain their extreme values. Therefore, the deformation and the equivalent stress can be observed at any instant of this duration. Fig. 11(a) and (b) show the deformation and the equivalent stress, respectively, of the electromagnetic shell steering system model at 3.8 ms. From the figure, the maximum deformation of the coaxial rudder is 0.013 mm owing to its weak stiffness and the maximum equivalent stress (103.08 MPa) occurs on the cylinder wall. However, the maximum equivalent stress is significantly less than the 785 MPa yield strength of 40 Cr. The actuator system of the electromagnetic shell did not undergo plastic deformation under the longitudinal impact load. Thus, it meets the structural strength requirements of longitudinal high-overload resistance.

Fig. 10Model of electromagnetic shell steering gear system under longitudinal transient impact load

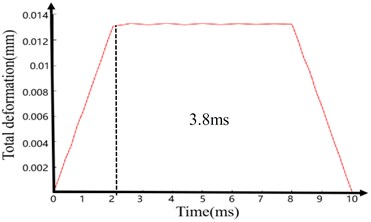
a) Time-deformation curve

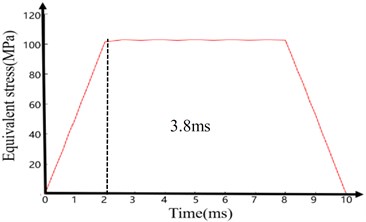
b) Time-equivalent stress curve

Fig. 11Longitudinal transient impact electromagnetic shell steering system model at 3.8 ms

a) Deformation

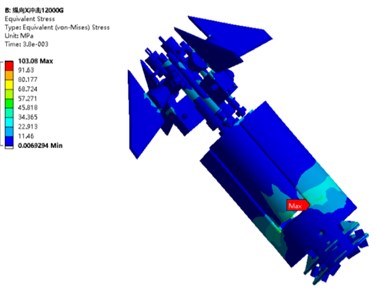
b) Equivalent stress

3.2.2. Lateral transient impact analysis

A transverse (positive $y$-axis) transient impact acceleration of 4000 g was applied to the steering gear model of the electromagnetic shell, and the high-strength screws between the motor and potentiometer and the cylinder wall were fixedly connected. The eight bolt holes of the cylinder wall were fully constrained. The impact time was set as 10 ms, during which the projectile rises for 2 ms, stays in orbit for 6 ms, and falls for 2 ms. Fig. 12(a) and (b) show the lateral transient impact analysis boundary conditions and diagram of the transverse transient impact time load, respectively.

The analysis results are shown in Fig. 13 and Fig. 14. Fig. 13 shows the dynamic characteristic curve of the maximum deformation and equivalent stress of the steering gear system model of the electromagnetic shell under the transverse transient impact load. At 0-2 ms, the system responds rapidly, and its maximum deformation and equivalent stress increase rapidly (0.059 mm for total deformation and approximately 108 MPa for equivalent stress). When the 4000 g transient impact load is removed, the maximum deformation and equivalent stress fluctuate slightly until 8 ms. Subsequently, the deformation and equivalent stress decrease to 1.17e-3 mm and 2.218 MPa, respectively.

Fig. 12a) Lateral transient impact analysis boundary conditions; b) lateral transient impact time load diagram

a)

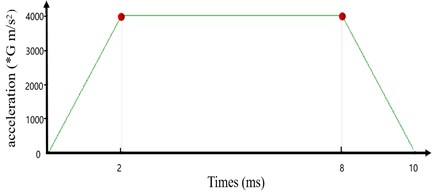
b)

Fig. 13Model of electromagnetic shell steering gear system under transverse transient impact load

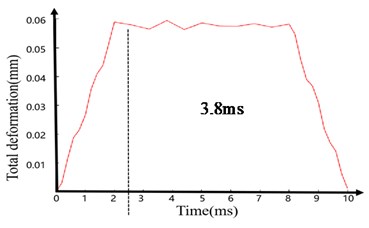
a) Time-deformation curve

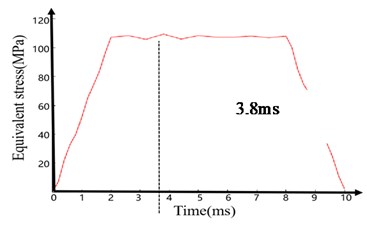
b) Time-equivalent stress curve

Fig. 14Transverse transient impact electromagnetic shell steering system model at 3.8 ms

a) Deformation

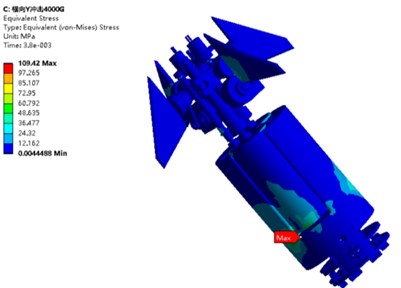
b) Equivalent stress

For the longitudinal transient impact analysis, the deformation and the equivalent stress of the electromagnetic shell steering gear system model under the transverse transient impact load at 3.8 ms were considered, as shown in Fig. 14(a) and (b). As shown in the figure, the maximum deformation occurs on the coaxial rudder blade, reaching 0.059 mm; this indicates an increase of 3.5 times compared with the deformation of 0.013 mm under the longitudinal transient impact. This is because the transverse stiffness of the steering system model of electromagnetic shell is less than the longitudinal stiffness. The maximum equivalent stress (109.42 MPa) also occurs on the cylinder wall, which is significantly less than the yield strength of 40 Cr at 785 MPa. The electromagnetic shell steering system did not undergo plastic deformation under the transverse impact load, thereby indicating that it meets the structural strength requirements of transverse high-overload resistance.

4.1. Establishment of mathematical model of electric actuator system for anti-high-overload electromagnetic shell

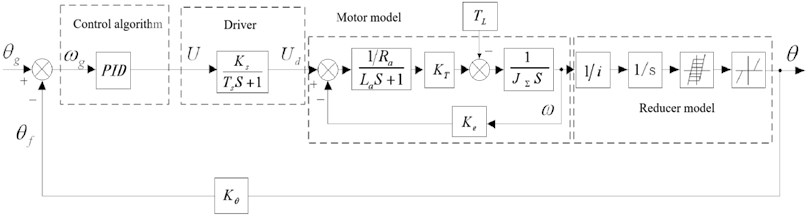
To achieve fast tracking command response and a high-precision index for the electric actuator system of the anti-high-overload electromagnetic shell, a dynamic mathematical model of the actuator system was established, and the transfer function of each part was calculated. The mathematical model block diagram of the electromagnetic shell electric actuator is shown in Fig. 15. The first, second, third, and fourth dotted boxes represent the PID control algorithm, drive model, motor model, and reducer model parts, respectively.

Fig. 15Mathematical model block diagram of electric actuator

4.2. Mathematical model simulation of the electric actuator of the electromagnetic shell with high-overload resistance

Using MATLAB/Simulink, the data were incorporated into the mathematical model of the electric actuator system.

Under the application of an external load moment $T_L=0$, the open-loop and closed-loop transfer functions of the electric actuator are shown in Eq. (10) and Eq. (11) respectively:

The motor parameters are as follows: rated power $W=$ 15 W, rated voltage $U=$ 24 V, maximum current $I=$ 2.7 A, rated speed $V=$ 5000 RPM, rated torque $M=$ 30 N⋅mm, motor internal resistance$R=$ 7.53 Ω, locked rotor current 18 A, speed constant $K_e=$ 208 RPM/V, mechanical time constant = 9 ms, total reduction ratio $i=$ 85, and total delay of driver = 0.1 ms.

Since the rated voltage is 24 V and the rated speed of the actual motor is 5000 r/min, the motor back EMF constant is shown in Eq. (12):

When the rated electromagnetic torque of the motor is 30 N⋅mm, the motor current is 0.650 A. The torque constant of the motor is shown in Eq. (13):

The motor rotor inertia is $J_M=$ 12×10^-7 K and load inertia is $J_L=$ 1.5×10^-3 K. The equivalent motor inertia is shown in Eq. (14):

The mathematical model of the motor obtained with the above data is shown in Fig. 16.

Fig. 16Motor model

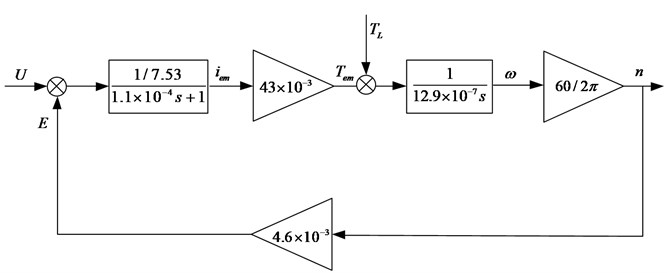
The transfer function of the motor model is shown in Eq. (15):

By omitting the higher-order terms and simplifying the equation, we obtain the following:

The total delay of the H-bridge was calculated according to the following formula, and the H-bridge model is shown in Fig. 17.

Fig. 17H bridge model

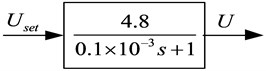
We used MATLAB/Simulink to build the overall mathematical simulation model of the electric actuator, which is shown in Fig. 18.

The given position is used as the input signal, and the position feedback is considered as the output. Its transfer function is shown in Eq. (17):

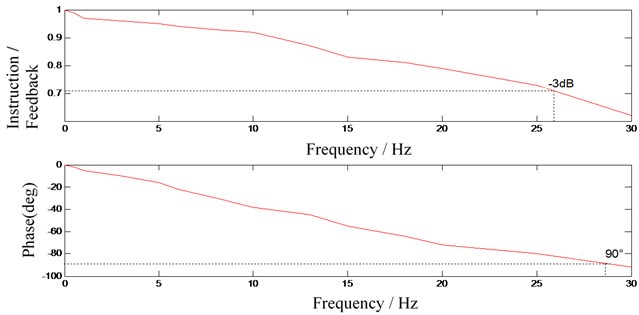
In practical engineering problems, Bode diagrams are frequently used to analyze the frequency characteristics of systems. The Bode diagram of the transfer function of the proposed system was obtained using MATLAB and is shown in Fig. 19.

According to the Bode diagram, when the system gain is –3 dB, the system frequency is 29.9 Hz, and phase delay is –45.9°. The simulation results show that the system response tracking is good; the bandwidth reaches 26 Hz; the rise time and overshoot of the system step response are within the index range; the dynamic characteristics are good; and the requirements of the project indicators are met well.

Fig. 18Simulation model of electric actuator

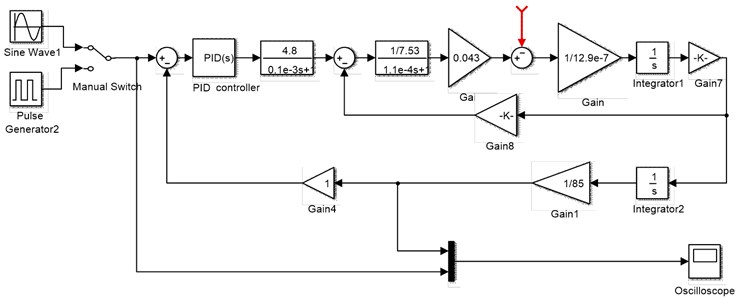
Fig. 19Bode diagram of steering gear system

5.1. Analysis of maximum mechanical rudder deflection angle

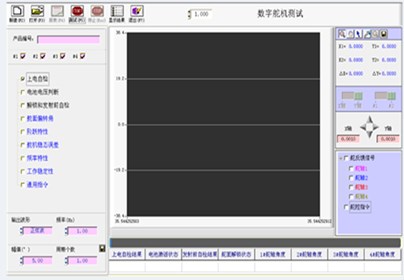
The maximum rudder deflection angle of the steering gear mainly depends on the effective electric stroke of the potentiometer and the mechanical stroke of the reducer. To verify the design requirements of the maximum rudder angle of the new high-overload electromagnetic shell actuator, the actuator controller sent sine wave commands with an amplitude of ±15° and a frequency of 0.50 Hz. The maximum rudder deflection test results are shown in Fig. 21. As evident from the figure, the feedback signal exhibits the variation characteristics of the input signal of the control system. The amplitude of the feedback signal has no attenuation, and the phase delay is 10°. The maximum rudder deflection angle meets the design requirements shown in Table 1.

Fig. 20Prototype and test system of new high overload electromagnetic shell steering gear

a) Electromagnetic shell electric steering gear prototype

b) Test software interface

Fig. 21Test results of maximum rudder deflection angle

5.2. Frequency response characteristic analysis

To verify the frequency response characteristics of the new high-overload electromagnetic shell actuator, the master computer sent various sinusoidal signals at frequencies of 1-30 Hz to the actuator controller. The signal amplitude and sampling frequency were ±2.5° and 1000 Hz, respectively. Fig. 22 shows the test results obtained using sinusoidal signals at 30 Hz. To improve the comprehensibility of the frequency response test results, the amplitude attenuation and phase-shift curves corresponding to each frequency are shown in Fig. 23.

According to the curves of the amplitude attenuation and phase shift corresponding to each frequency in Fig. 23, when the amplitude is 2.5° and the input signal frequency is 1-30 Hz, the response characteristics of the system are satisfactory. With an increase in the input signal frequency, both the attenuation of the output signal and the phase delay increase gradually. When the sinusoidal frequency reaches 26 Hz, the amplitude attenuation of the output signal is close to 30 %, and its phase lag is less than 90°. The test results satisfy the performance requirements listed in Table 1.

Fig. 22Test results with frequency of 30 Hz

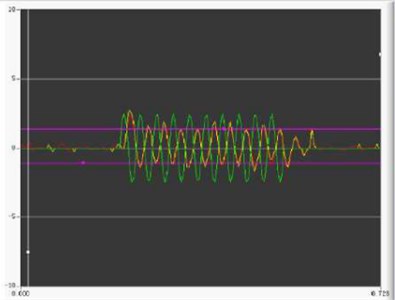
Fig. 23Amplitude attenuation and phase shift curve of each frequency

5.3. Analysis of step response characteristics

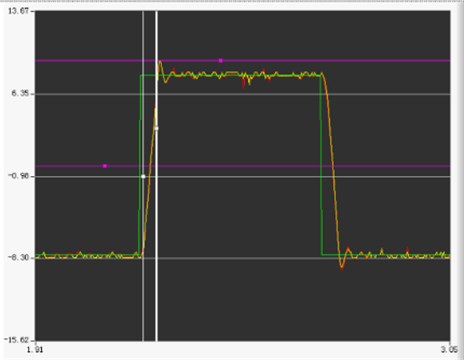
To verify the step response characteristics of the proposed high-overload electromagnetic shell actuator, the master computer sent an 8° square wave signal to the actuator controller. The sampling frequency of the system was 1000 Hz. The step response characteristics of the electromagnetic shell actuator are shown in Fig. 24. It can be observed that the time required for the rudder blade deflection to change from 0° to 8° is approximately 40 ms, which is within the required 60 ms, according to the design index in Table 1. The overshoot is 12.5 %, which is within the 20 % stipulated as per the design index. The maximum steering angle velocity of the steering gear is 198.46 °/s, which is lower than the design requirement of 200 °/s.

A comparison of the test results of the maximum rudder deflection angle and the frequency and step response characteristics of the experimental prototype with the simulation results of the system dynamic characteristics shows that the performance index of the test results is lower than that of the simulation results, but it still meets the requirements of the design index. Thus, the dynamic characteristic model of the actuator system of the proposed electromagnetic shell is validated. From the test results, we can observe that the servo system designed in this study performs satisfactory response tracking. The frequency response bandwidth of the system can reach 26 Hz, which meets the requirement of 25 Hz. The step response overshoot and rise time of the system are also within the requirements of the indicators.

The above analysis indicates that the proposed high-overload electromagnetic shell steering system has good dynamic characteristics and meets the design requirements.

Fig. 24Step response test results