Abstract
An attempt is made to establish the dependence of the timbre of the Sarasvati veena, a South Indian string instrument, on its extended bridge. The equation of motion for a plucked string vibrating against the extended boundary at the bridge is solved numerically. The solution is analyzed for timbre characteristics, which show energy redistribution among the higher harmonics, as well as revival of higher harmonics with time. The variation of timbre with bridge slope and curvature are analyzed. These results are validated by comparison with corresponding analysis of acoustic data gathered from experiments performed on a sonometer, whose knife edge is replaced by the bridge of the veena.
Highlights
- Tension in the string has a effect on the acoustic spectrum of plucked string. Optimum tension has to be considered for the good performance of the stringed musical instrument.
- Numerical model developed for the simulation of motion of plucked string against the extended bridge of Veena is validated by experimental results.
- Vibration of plucked string against the extended of bridge of veena distributes the energy among the harmonics and enhances the significance of higher harmonics in its acoustic spectrum.
- Extended bridge is also responsible for the revival of higher harmonics over a time.
- Profile (shape top surface coming in the contact of plucked string) of bridge has a huge impact on the timber of Veena.
1. Introduction
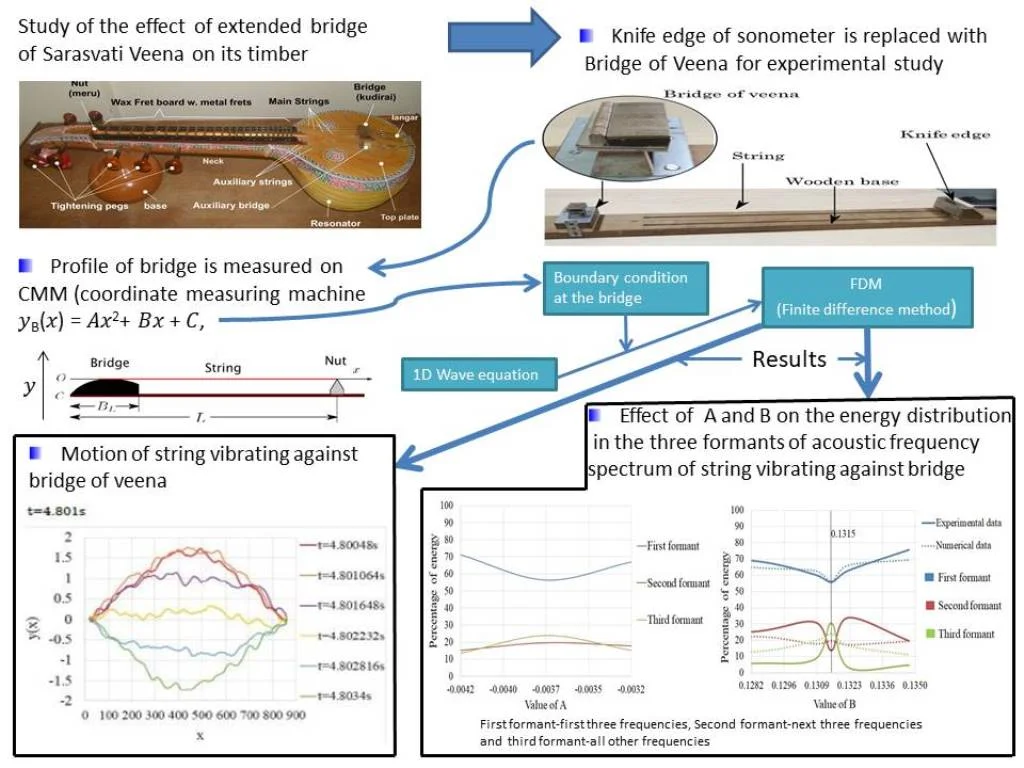
The Sarasvati veena of South India (Fig. 1) is a classical plucked stringed musical instrument of historic precedence. This instrument is a fretted lute mainly carved out of the hard wood of a seasoned jackfruit tree. It has a large bowl-shaped resonant chamber (kudam or “pot”), which continues into a long hollow neck (dandi). Cylindrical bell-metal frets, 24 in number, are fixed to the fretboard on a ledge made of a hardened mixture of beeswax and charcoal powder. The positions of the frets are determined by harmonic tuning derived in consonance with string vibrations, in contrast to the equitempered scale on western instruments [1]. The veena has four main playing strings that are fixed at one end, and stretched over an extended bridge. There is a high wooden structure (kudirai or “horse”) topped by a plate made of bellmetal. The strings then pass over the frets and finally over a cylindrical metal nut (meru) and are held by wooden tuning pegs (birudai). Below the nut, a hollow stand made of fibre or papermache (originally dried pumpkin rind called surakkai), is attached, whose purpose is to support the veena in the horizontal position. The veena also has three side strings that do not pass over the frets, and are used to provide an accompanying drone.
The veena has played a special role in the development of South Indian music and musicology. According to musicology literature such as Sangeeta Ratnakara [2], the timbre of this instrument is said to be close to that of the human voice, and its harmonic structure was the basis of development of the musical grammar. The distinctive rich and multi-harmonic timbre of this instrument has been assumed to be due to the extended bell-metal bridge, round metal frets and the wooden resonant chamber.
Sir C V Raman [3] was the first to attribute the timbre of Indian string instruments to the bridge. He suggested that the bridge caused energy transfer from the fundamental to higher harmonics, and that this needed further investigation. He also showed the violation of the Young-Helmholtz law. So we started a programme aimed at fully characterizing the Sarasvati veena, both numerically and experimentally. We wished to characterize the timbre, and to ascertain the contribution of the bridge, as well as other structural features such as the resonant cavity and the frets. The Tanjavur veena is traditionally manufactured by artisans who analyze the sound by ear and make minor structural adjustments to achieve the desired timbre [4]. In our work, we attempt to standardize its construction for a musically perfect instrument.
Fig. 1The Sarasvati veena
The current work focuses on how vibrations of a string against the extended bridge of Sarasvati veena give rise to the spectral characteristics of this instrument. We performed analysis of acoustic data obtained from a string vibrating against the veena bridge installed on one end of a sonometer. The main features of the veena timbre were reproduced by the numerical simulation and were verified experimentally. Analysis of the timbre variation with change in bridge parameters such as slope and curvature showcases the major role played by the bridge in imparting the characteristic tonal quality to the veena. Raman’s hypothesis regarding redistribution of energy to the higher harmonics, as well as violation of Young-Helmholtz law, is validated. We made a preliminary numerical model to try to understand the origin of these effects. We use a parabolic boundary on one end for the one-dimensional wave equation and solve it numerically by the finite difference method (FDM) implemented on MATLAB [5]. The solutions so obtained are analyzed for timbre characteristics. The broad features of the experimental results are corroborated by the basic numerical model, which does not incorporate contact forces and sticking between string and bridge. Collision of string with the bridge is considered as perfectly elastic.
Eastern musical instruments like Sitar, Tanpura, Biwa etc. have been studied earlier [6-9]. In other work, [10, 11, 8] the effect of an extended bridge on musical instruments such as Sitar and Tanpura has been studied. These authors use variational methods to modify the one-dimensional wave equation subject to a constraint at one end, whose solution is simulated numerically. In the work by [12], the interaction of the string with the bridge has been considered as a collision and solutions have been simulated using non-smooth contact dynamics. The acoustic properties of the sitar have been studied in the work by [13] using a physical model with special emphasis on the non-linearity of string motion due to its interaction with the extended bridge. Wahi et al. [14] have theoretically studied the role of curvature in determining characteristics of the string vibrating against a doubly curved bridge. They find that this obstacle has a destabilizing effect on the plane motion of the string. In work on the piano string by [15], the influence of contact nonlinearity on the spectral structure of the vibration is studied numerically. The growth and extension of high frequency oscillations are observed and are attributed to the parabolic shape of the capo bar of the piano. This simulation also explains the missing modes in the piano. This work, as well as Raman’s work has made room for further experimental investigation of the role of a parabolic bridge.
2. Preliminary studies on the Timbre
In our earlier work [16], we had performed preliminary studies on the timbre of a Tanjavur Sarasvati veena, by studying the acoustic Fourier spectrum. The results showed that the spectrum is harmonic in nature. The maximum power is in the harmonic that is closest to the resonant frequency of the body. The higher harmonics have significant power, which leads to the richness of timbre. We also studied the spectrum under different working conditions: (a) each of the seven strings on the instrument, with standard tuning, (b) varying tension in the main string, and (c) varying speaking length of the main string, by changing the point of contact with the frets. Broadly, the same behavior is observed in each case, which includes all the possible situations while playing the instrument.
Further [17], we had performed acoustic analysis of the veena strings and vibrational analysis of the body, to establish the optimum tuning frequency of the instrument, as that which gives the richest timbre. A surprising observation was that the optimum tuning frequency was close to half the natural frequency of the whole structure, as obtained from impact studies.
Subsequently, we compared the acoustic spectrum of the veena to that of a simple sonometer to identify its unique timbre [18]. We found that the acoustic spectrum has more harmonic content as compared to sonometer. Also, some harmonics specially the higher ones show revival after some time in case of veena. Study brought us to conclusion that veena has rich and unique timber which enhances with the time, this characteristic timber can be related to the presence of extended bridge and resonator of Sarasvati veena.
These observations are to be substantiated by extensive studies of the interaction of the vibrating string with the extended bridge and the resonant cavity. In the current work we focus on the bridge. The effect of the resonator is studied in another work.
3. Methodology
We find numerical solutions to the one-dimensional wave equation for the string, subjected to boundary conditions at one end given by the shape of the bridge profile, and fixed at a point on the other end.
In this numerical simulation we assume that the string motion is not subject to any additional force at the bridge, such as contact force, sticking etc. The purpose served by the bridge is to restrict the region of motion of the string at that end. This implies that the collision of the string with the bridge is perfectly elastic. This forms a basic model to guide our numerical study. Experimental validation of numerical results requires same physical environment as considered during numerical analysis. Experimental analysis is performed on a sonometer with one of its knife edge replaced by bridge of Sarasvati veena; this modification helps to study string bridge interaction only and eliminating effect of resonator.
We use standard playing conditions for the purpose of this study. The main playing string is considered, with standard material properties of steel. This gives us the tension and the speed of wave propagation to be used in the simulation.
3.1. Modeling the curved bridge
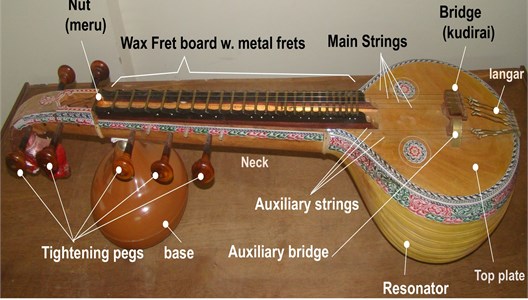
The bridge of the veena is shown in Fig. 2(a). The equation for the bridge profile was experimentally obtained using the Mitutoya Coordinate Measuring Machine (CMM 574). Measurements were made across different cross-sections of the bridge and averaged. The best-fit curve was given by the following parabolic equation:
where the curvature is −0.0037; slope is 0.1315; intercept with -axis −1.1579, and the length of the bridge is 25.855mm.
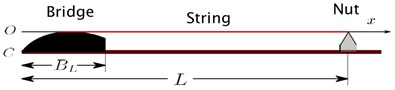
Fig. 2a) Extended bridge of the veena, b) coordinate system

a)
b)
3.2. Modeling and simulation of string vibrations
We started with the simple one-dimensional damped wave equation:
Given linear mass density 0.56 g/m and tension 48.5 N in the main playing string tuned to the frequency of 175 Hz, the wave velocity was calculated to be 294.315m/s. For our system, the equivalent viscous damping coefficient was obtained empirically from the logarithmic decrement of the time signal of the acoustic data.
The coordinate system used for the simulation is shown in Fig. 2(b).
The veena is normally played by plucking with a metal plectrum at a point close to the extended bridge. The plucking action is mainly a vertical displacement by a small amount. These conditions are used as initial conditions for our simulation: the string is displaced by 5 mm at a point located at 0.17 where 84.5 cm is the total sounding length of the string. The boundary condition at the playing side is given by the equation of the bridge, which ensures that the string motion is constrained in that region. This boundary condition is incorporated by the following pseudo code:
for
if
then
Where, is given by Eq. (1). The effect of constrain at a position and time is propagated to the next step, thus there is a position- and time- varying condition at that end of the string. This is incorporated at each step of the iteration. The spectrum of the solution obtained numerically was then analyzed.
3.3. Finite difference method scheme
The Eq. (2) was solved by the explicit method of solving a hyperbolic partial differential equation. The explicit scheme is conditionally stable under certain conditions. The wave equation is written in terms of discretized displacement labeled by spatial index and time step index :
If is the time step in sec, is the spatial step in m and is the wave velocity in m/s, then we have:
The solution to this equation in the explicit scheme is conditionally stable under the conditions:
We have used 1 and 294.315 m/s to get the equation:
Convergence was tested starting with 0.00001s and we arrived at: 0.000002 s and 0.00058862 m.
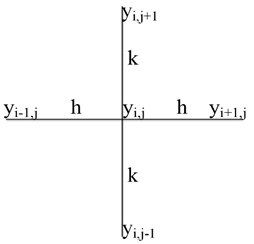
The stencil for the FDM is as shown in Fig. 3.
Fig. 3Stencil for FDM
3.4. Model for experimentation
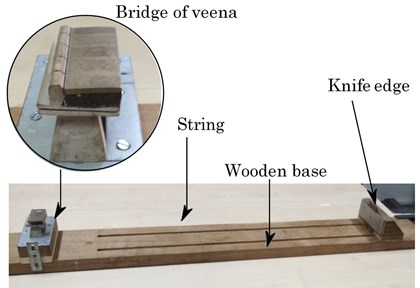
In order to validate the numerical results, we built an experimental setup that mimics the assumptions of the theoretical model. We constructed a simple sonometer (without resonator) with a knife edge at one end and the actual veena bridge mounted at the other end. (See Fig. 4). Thus we eliminated the effect of the other structural details of the veena.
Fig. 4Modified sonometer with veena bridge
3.5. Experimentation
We analyzed data gathered for plucked string vibrations on the sonometer with veena bridge. Experiments were conducted in a semi-anechoic chamber. We used the standard veena string of steel with gauge 31 (diameter 0.3 mm). The string was plucked using a metallic wire plectrum at 0.17. We ensured plucking amplitude of around 5 mm in the vertical plane. We measured the sound pressure amplitude created near the point of plucking. We used a 1/4” microphone (model no. 378C01, PCB Electronics, USA) which has sensitivity of 2.29 mV/Pa. The string was tuned to frequency 175 Hz. In accordance with standard experimental methods of acoustics and vibrations [19], eight runs were recorded, normalized and averaged for analysis. Data obtained by these tests were recorded by Vibration Analyzer (Spider-81, Crystal Instruments, USA) and the obtained results were then analyzed using Engineering Data Management Software.
From the logarithmic decrement of the time signal, the equivalent viscous damping coefficient was obtained to be 105.3 Ns/m. This was the value of b used in numerical simulation of Eq. (2). For comparison, we gathered similar data under the same conditions for the simple sonometer as well as the veena.
4. Analysis of timbre
We analyzed the variation of timbre with the following parameters under our control: (A) string length and tension, (B) slope of the bridge and curvature of the bridge.
4.1. Effect of string length and tension on the timber of the Sarasvati veena
In order to study the dependence of timbre on string tension, we performed acoustic experiments on the sonometer, both with knife edge, and with veena bridge.
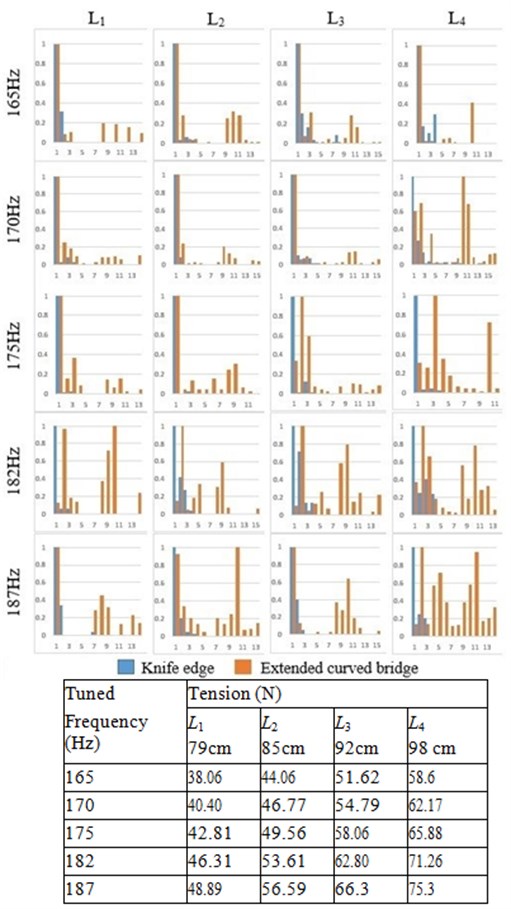
For four different string lengths on the sonometer, we adjusted the tension to obtain five different fundamental frequencies and analyzed the FFT of the acoustic data. The normalized amplitude of the spectrum for each case are plotted for both knife edge and veena bridge in Fig. 5. The results show that there is significant redistribution of energy into the higher harmonics for the veena bridge, as compared to the sonometer with knife edge, in which most of the energy is concentrated within the first four harmonics. We also observe that the greater the tension, more the presence of higher harmonics in the case of veena bridge. However, from the musical perspective, excessive presence of higher harmonics produces a shriller sound, that is not considered favorably (Ayyangar, 1978). Also, for playing the veena, high tension is not preferred since it makes it more difficult to play by bending the string. For the numerical simulation, we therefore decided to analyze the timbre corresponding to the optimal tuning frequency of 175 Hz alone, since the veena as a whole responds more richly to this frequency [17].
4.2. Effect of presence of Bridge
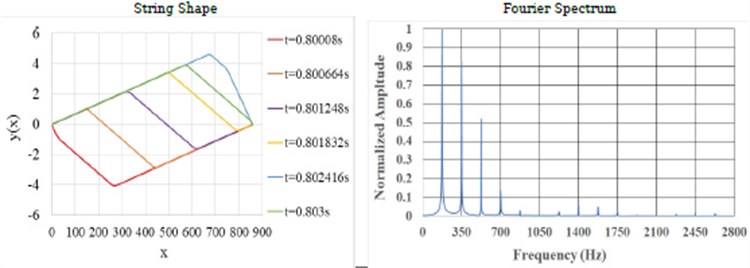
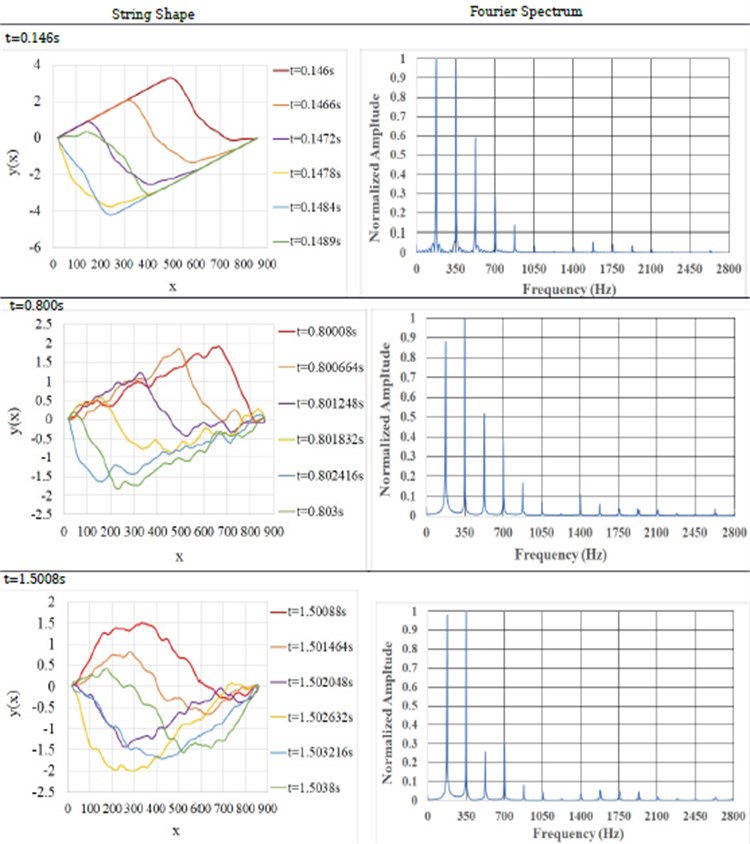
The FDM solution to the damped equation of motion (Eq. (2)) is studied for time period of 5 s. The presence of the bridge is found to curtail the motion in one direction. The solution settles down to a sustain mode after about 2 sec. We analyzed the FFT spectra of the motion of string over some selected time periods (picked from preliminary studies [18]) and compared with the corresponding periods for the sonometer. This analysis shows how the presence of bridge causes harmonics to develop over time. The results are displayed in Fig. 6(b).
The string motion of the sonometer shows the same behavior over all time intervals. As a representative, we display the string motion and FFT for one time period after 0.8 s in Fig. 6(a). We see that the FFT of the string with bridge has more harmonic content than that of sonometer.
Further, as time progresses, the shape of the string becomes more complex, and the energy in the spectrum gets redistributed over higher harmonics. This is seen to be a consequence of the mere presence of the bridge.
Fig. 5Normalized amplitude of FFT as a function of harmonics: comparison of sonometer with knife edge vs extended veena bridge, for different tensions and string lengths
The spectral energy distribution and its variation with time give rise to the typical timbre (naada) of the veena. The importance of the bridge in contributing to the desired timbre is often stressed by veena makers, who warn the user to take special care of the bridge and not disturb it in any way.
A good way to capture the veena timbre is by its formant structure. We select the three major frequency ranges in which energy is concentrated, as forming the three formants for the veena. Here we have considered the fundamental and first two harmonics as constituting the first formant, the next three harmonics constituting the second formant, and all the higher frequencies are clubbed in the third formant. The energy content in each formant is obtained from the power spectrum of the acoustic signal, as also from the FFT of the numerical solution. For comparison, the energy distribution in the formants of the veena was also obtained experimentally.
Fig. 6a) String motion and FFT of simple sonometer: FDM simulation b) string motion against veena bridge over one time period, at different times, and corresponding FFT
a)
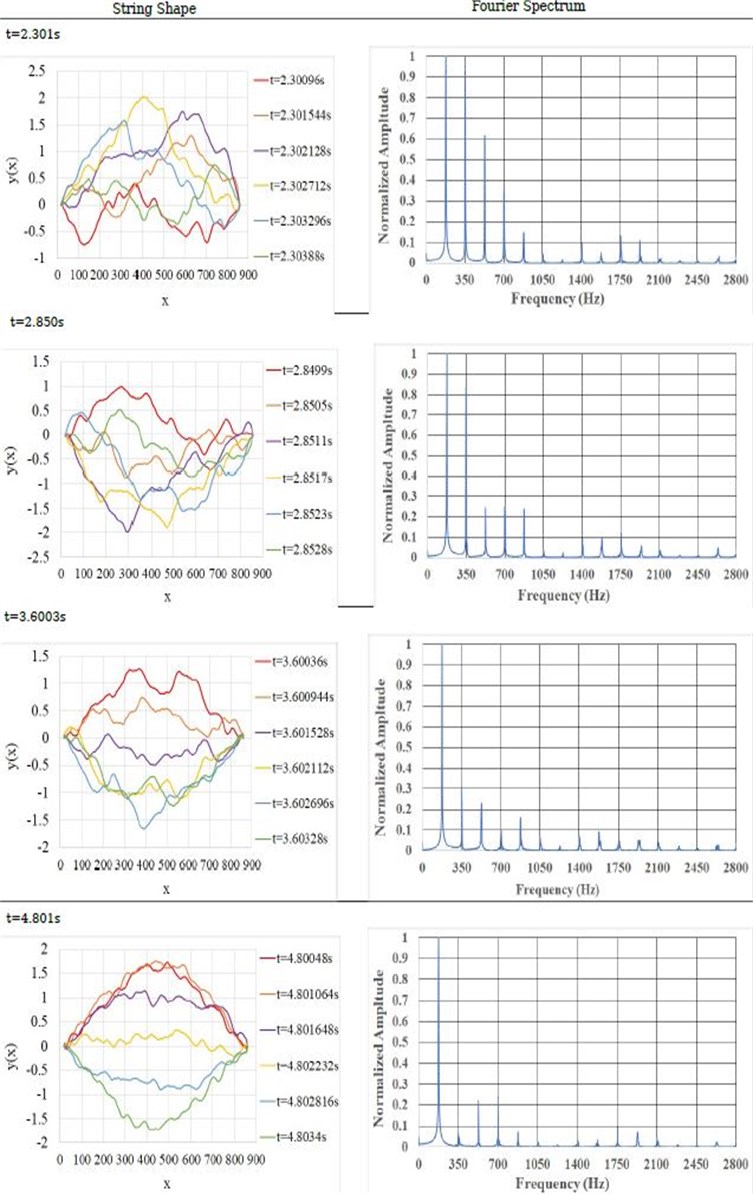
b)
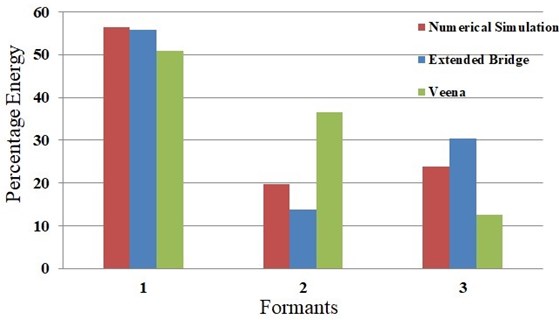
Experimental results from veena are compared with experimental results from simple sonometer and numerical results from sonometer with extended bridge. The results are shown in Fig. 7. For sonometer most of the energy lies in a first formant, while sonometer with extended bridge shows distribution of energy among three formants. For the actual veena, the second formant has greater energy than the third formant. This can be attributed to the presence of the resonator, and is being further explored.
Fig. 7Comparison of energy distribution in the three formants for numerical simulation, experiment on extended bridge, and Sarasvati veena
The contribution to the timbre by bridge parameters, i.e. its slope and curvature were further explored. In the numerical simulation, we varied the slope and the curvature in the bridge Eq. (1). To validate the results experimentally, we could change the value of the bridge.
We did this by tilting the bridge, by inserting slip gauges of known thickness below one edge of the bridge. We then measured the exact slope using CMM. We also used the same values for in the numerical simulation.
Experimentally varying the curvature, , was not possible since changing curvature means involves manufacturing several new bridges. We did not have the material or means for manufacturing new bridges.
4.3. Variation of timbre with bridge slope and curvature
4.3.1. Effect of varying slope
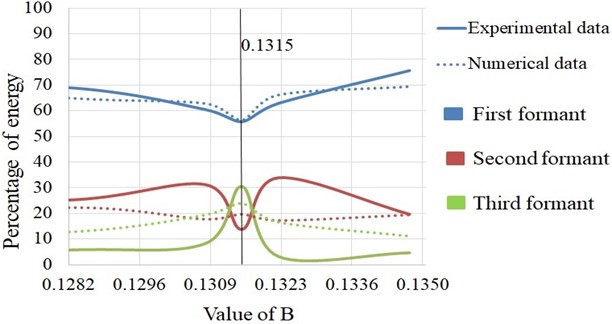
We studied the formant structure for five different values of while keeping constant at the experimentally measured value of −0.0037. Fig. 8 shows the variation of energy content in three formants with varying bridge slope , for numerical simulation as well as for experimental acoustic data.
It is found that the effect of the bridge is to redistribute the energy among the three formants. We see that this effect reduces as the B value increases or decreases from the value 0.1315, for the veena bridge we used. This indicates how the wrapping and unwrapping of the string over the bridge affect its timbre, depending on the slope at the point of contact.
In our numerical solution of Eq. (2), the energy content is 56.4 % in the first formant, 19.7 % in the second formant and 23.9 % in the third formant. Thus, there is substantial energy in the higher harmonics. The experimental results show 55.7 % in the first formant, 13.8 % in the second formant and 30.5 % in the third formant. Note that the experimental data is acoustic whereas the numerical data is of mechanical vibrations. The difference between simulation and experimental results may be attributed to the frequency dependence of the structural damping, which we have not taken into account in our numerical model [20]. We have also not considered the effect of acoustic dispersion [13]. This is the subject of active investigation currently.
From these results, we can say that the slope of the bridge has significant effect on the timbre.
Fig. 8Relation between energy distribution in three formants and value of bridge slope (B)
4.3.2. Effect of varying curvature
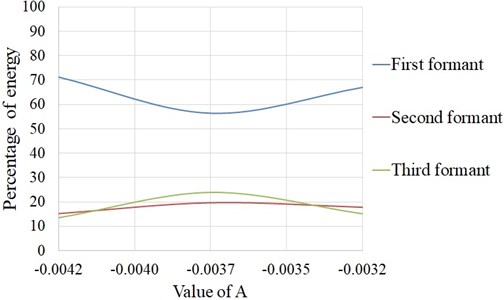
We varied the curvature from –0.0037 to –0.0047 numerically, while keeping the slope at its experimentally measured value of 0.1315. Results are plotted for variation in energy content in the three formants with varying bridge curvature.
It is observed from Fig. 9 that curvature of bridge contribute to the distribution of energy among three formants. At 0.0037 more energy content is distributed in second and third formants as compared to other values of bridge curvature.
Fig. 9Energy distribution in three formants for different values of bridge curvature (A), numerical simulation
5. Results and discussion
This work attempts to analyze the contribution of the extended bridge to timbre of the Sarasvati veena, by numerically as well as experimentally modelling the string vibrations against the veena bridge. The numerical solution was found to be harmonic, which was verified experimentally. The key features of string vibrations against the veena bridge are captured by our solution.
The basic harmonic character of the timbre is observed, regardless of the length of the string or its tension. So further analysis is restricted to optimal tension value alone. The presence of the bridge brings out the higher harmonics in greater strength. This is attributed to the development of complex motion of the string over time (Fig. 6(b)). In fact, we find that almost all harmonics are excited. Odd as well as even harmonics are observed, violating the Young-Helmholtz law, which was first pointed out by [3].
The characteristic timbre of the veena as described by its formant structure [18] is also corroborated in our numerical study, as summarized in Fig. 7. In the sonometer, most of the energy lies in the first formant. When the bridge is introduced, this energy is redistributed into second and third formants. We observed that for 0.1315 and 0.0037, more energy is found in second and third formants as compared to other values of B and A respectively.
Thus, the timbre of the veena can be largely attributed to the extended bridge and it is sensitive to the slope and curvature of the bridge.
6. Conclusions
Increasing the tension in veena string leads to presence of higher harmonics with stronger amplitude, however excessive higher harmonics are undesirable (due to shriller sound). So study of effect of extended bridge of Sarasvati veena on its timber was carried out at optimum tuning frequency of 175Hz. It was found that slope and curvature and bridge have a major role in the timber of an instrument. Slope, 0.1315 and curvature –0.0037 of the bridge are found to be optimum values to obtain harmonically rich timber out of the veena we used to study.
Finer details would involve incorporation of dispersion. Further details of the veena spectrum, such as the enhancement of the second format, can be attributed to the resonant cavity and other structural details of the veena. These form the subject of ongoing study.
References
-
Chauhan C., Singru P. M., Vathsan Radhika Experimental basis of the concept of Sruti (microtones) in Indian classical music using the Sarasvati Veena. 25th International Congress on Sound and Vibration, 2018.
-
Rangaramanuja Ayyangar R. Sangita Ratnakara of Sarngadeva: A Study. Vipanci Charitable trust, 1978.
-
Raman C. V. On some Indian stringed instruments. Proceedings of the Indian Association for the Cultivation of Science, Vol. 33, 1921, p. 29-33.
-
Thanjavur Musical Instruments Workers Co-operative Cottage Industrial Society Ltd. Registration as Geographical Indications of Goods for the Thanjavur Veenai (Tanjore Veena). Journal of Geographical Indications (India), Vol. 48, 2013.
-
Erwin Kreyszig Advanced Engineering Mathematics. 8th edition, John Wiley and Sons, 2006.
-
Tomoyasu Taguti, Yoshimasa Kakuryo Tohnai Acoustical analysis on the sawari tone of Chikuzen biwa. Acoustical Science and Technology, Vol. 22, 2001, p. 199-207.
-
Robert Burridge, Jay Kappraff, Christine Morshedi The sitar string, a vibrating string with a one-sided inelastic constraint. SIAM Journal on Applied Mathematics, Vol. 42, Issue 6, 1982, p. 1231-1251.
-
Chandrika P Vyasarayani, Stephen Birkett, John Mcphee Modeling the dynamics of a vibrating string with a finite distributed unilateral constraint: application to the sitar. The Journal of the Acoustical Society of America, Vol. 125, Issue 6, 2009, p. 3673-82.
-
Van Walstijn M., Chatziioannou V. Numerical Simulation of Tanpura String Vibrations. International Symposium on Musical Acoustics (ISMA 2014), Le Mans, France, 2014, p. 609-614.
-
Mandal A. K., Wahi P. Natural frequencies, modeshapes and modal interactions for strings vibrating against an obstacle: Relevance to Sitar and Veena. Journal of Sound and Vibration, Vol. 338, 2015, p. 42-59.
-
Mandal A. K., Wahi P. Mode-locking and improved harmonicity for real strings vibrating in the presence of a curved obstacle. Nonlinear Dynamics, Vol. 88, Issue 3, 2017, p. 2203-2224.
-
Issanchou Clara, Acary Vincent, Perignon Franck, Touze Cyril, Jean Loıc Le Carrou Nonsmooth contact dynamics for the numerical simulation of collisions in musical string instruments. Journal of the Acoustical Society of America, Vol. 143, Issue 5, 2018, p. 3195-3205.
-
Sadjad Siddiq A Physical Model of the Nonlinear Sitar String. Archives of Acoustics, Vol. 37, Issue 1, 2012, p. 73-79.
-
Harkirat Singh, Wahi P. Role of curvatures in determining the characteristics of a string vibrating against a doubly curved obstacle. Journal of Sound and Vibration, Vol. 402, 2017, p. 1-13.
-
Stulov Anatoli, Kartofelev Dmitri Vibration of strings with nonlinear supports. Applied Acoustics, Vol. 76, 2014, p. 223-229.
-
Samarth Mathur, Ayush Raizada, Pravin Singru M., Radhika Vathsan Experimental acoustic analysis of Sarasvati Veena. Proceedings of 2nd International and 17th National Conference on Machines and Mechanisms, 2015.
-
Akshay Sundar, Hancel P. V., Pravin Singru, Vathsan Radhika Study of Sarasvati Veena– a South Indian musical instrument using its vibro-acoustic signatures. Journal of Vibroengineering, Vol. 18, Issue 5, 2016, p. 1392-8716.
-
Chauhan C., Singru P. M., Vathsan Radhika Acoustic analysis of timbre of sarasvati veena in comparison to simple sonometer. 46th National Symposium on Acoustics, 2017.
-
Piersol Allan G., Paez Thomas L. Harris’ Shock and Vibration Handbook. The McGraw-Hill Companies, Inc., sixth edition, 2010.
-
Rao S. S. Mechanical Vibrations. Pearson Education. 4th edition, Dorling Kindersley Publication, 2011.
About this article
This research was supported by the Science and Engineering Research Board (DST-SERB) project number EMR/2016/002338.
