Abstract
Flexible beam structure is usually applied in various fields of engineering and industrial. There are few points of interest using flexible structure and one of the advantages is that its lighter compared to a rigid structure. Besides that, flexible beam also can save cost, reduce energy consumption, and improve operation safety. However, flexible beam structures are too sensitive and susceptible to with unwanted vibration that would cause damage or degradation to the structure system. Hence, to overcome the problem, appropriate modelling and controller for such systems should be developed. Currently, there are plenty of methods that have been developed by researchers to suppress undesired vibration. Based on previous studies, most researchers nowadays use system identification (SI) as a modelling technique to develop a dynamic model of flexible structure via swarm intelligence algorithm (SIA). Therefore, two type of algorithms was used in this work for modelling development of flexible beam structure, which are ant colony optimization (ACO) and cuckoo search algorithm (CSA). Based on the comparative results, CSA achieved the lowest mean square error (MSE) value of 6.1547×10-9 meanwhile ACO recorded a MSE of 1.0728×10-8. Moreover, CSA was deduced to be the best model for flexible beam structure because it achieved 95 % confidence level in correlation test and has excellent stability in pole-zero diagram system. Thus, CSA is a suitable algorithm to represent the real behavior of flexible beam structure in a system.
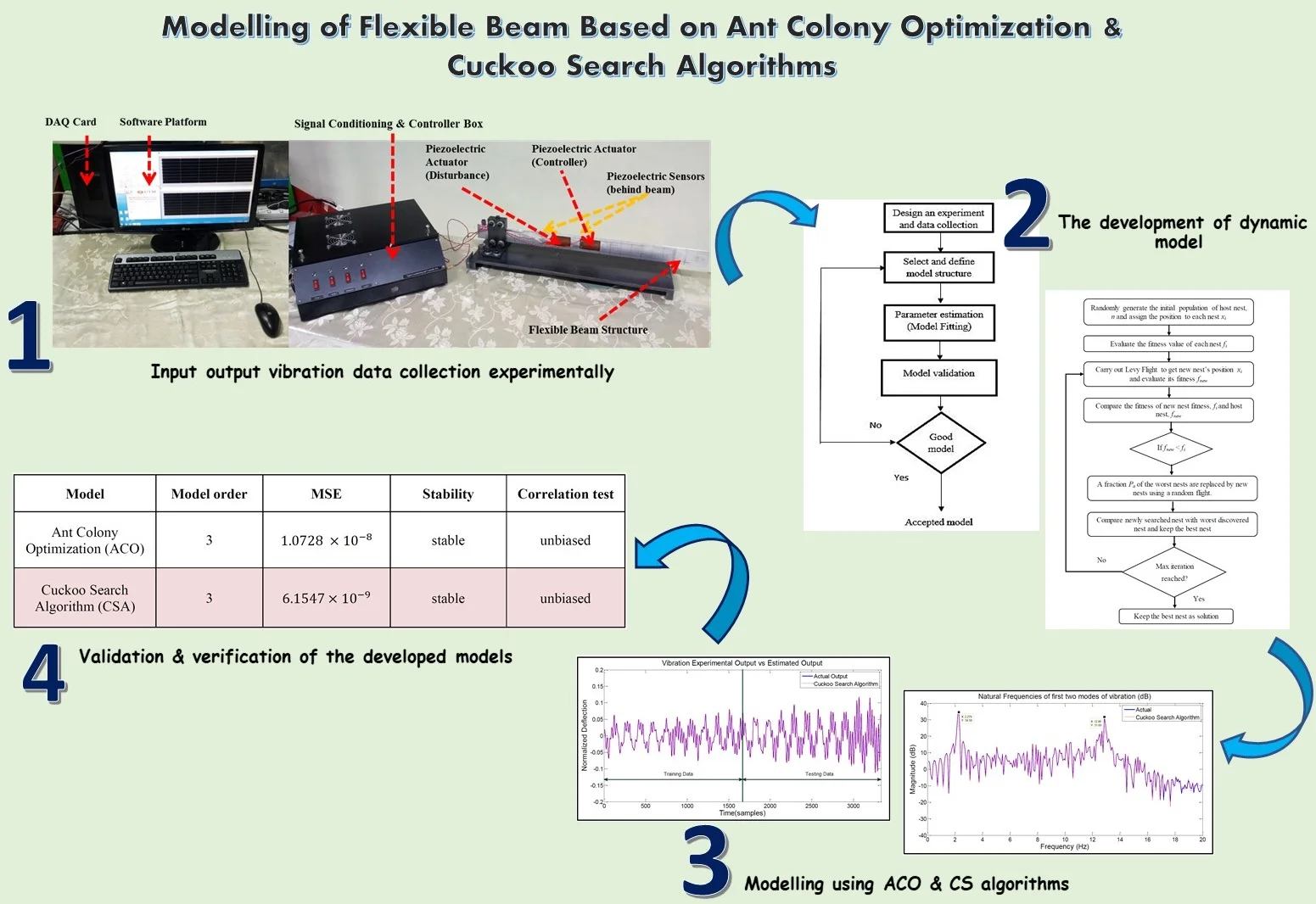
Highlights
- Input output vibration data collection experimentally
- The development of dynamic model
- Modelling using ACO and CS algorithms
- Validation and verification of the developed models
1. Introduction
In this new era of technology, a comprehensive usage a flexible beam structure in different fields of engineering and industrial manufacturer such as manufacturing of automobiles, aircraft, and architecture is evident because of its structural and material features [1]. More importantly, it is lightweight, reliable, efficient and provides better operation speed compared to rigid structure. In addition, it can be found in various shapes and sizes. Nowadays, flexible beam structure is an important element in manufacturing industries due to its advantages such as reducing manpower, inexpensive, faster movements, easy operation, and reduce accidents occurring at workspace [2]. Even though flexible structure has their advantages, the characteristics of a flexible beam still have limits as it is more sensitive and can be easily influenced by internal and external disturbances which led to unwanted vibration.
Excessive or unwanted vibration will cause problems including damage to machinery capability, bending, fatigue and degradation of performance [3]. Thus, it is necessary to eliminate undesirable vibration that exists in the flexible structure to maintain optimal performance. In order to diminish unwanted vibration on the flexible beam structure, proper modelling and efficient control needs to be designed to sustain the advantages and relevance of flexible beam structure in the industry. There are a few methods that has been proposed by previous researchers and academia to counter the issue of undesirable vibration in a flexible structure. Passive vibration control (PVC) is one of the techniques employed to suppress unwanted vibration for flexible structure since it is easy to handle and relatively inexpensive.
There are a few methods that has been proposed by previous researchers and academia to counter the issue of undesirable vibration in a flexible structure. Passive vibration control (PVC) is one of the techniques employed to suppress unwanted vibration for flexible structure since it is easy to handle and relatively inexpensive. Passive control strategy can be applied as a mechanical solution. Some examples include adding a vibration damper and any dynamic vibration absorber to the system. However, passive control is only functional for high frequency range system, as it does not perform well in low range frequencies [4]. Moreover, engineering applications demand for systems which are lightweight. The addition of such dampeners would further increase the system’s weight, hence practically unsuitable. Recently, active vibration control (AVC) technique can be considered as a promising method to reduce and control vibration since it is more efficient and reliable.
The principle of AVC, which was proposed by Lueg in early 1930’s revolves around mitigation of noise produced in a flexible system [5]. AVC is a technique that used actuator as an electronic element in the system to reduce the amplitude of an undesirable vibration by introducing a secondary source of vibration to the dynamic system [6]. In 2015, Yu and his friends carried out an experiment on fuzzy control of flexible beam structure using piezoelectric stack actuator to suppress vibration [7]. Other than that, Boonkurmkrong and his co-worker (2018) also studied on the application of back stepping boundary on a flexible beam to cancel undesired vibration [8]. Hence, this method is found to be more effective, accurate and inexpensive compared to passive control technique for cancellation of unwanted vibration. In addition, for flexible structure to achieve high performance, attaining an appropriate model of structure is necessary.
The first step to develop a model of the physical structure is via modelling of flexible beam by focusing on the behavior of the structure to acquire its dynamic response. This is to assist in the development of controllers to maintain the performance level of such structures [9]. Approximate modelling of flexible beam can be obtained by different methods. The common method used in literature are system identification (SI), finite element method (FEM), finite difference method (FDM) and partial differential equation (PDE). The FEM is a technique which solves the numerical problem in differential equations. Mirafzal and his friends (2015) stated that the frequency and mode shape of the beam can be obtained by derivation of the mathematical model from FEM through software simulation [10]. Besides that, FDM can be used to model a flexible beam since the mechanism is capable to understand lateral excitation force. A simulation of flexible beam via FDM can be easily implemented and the technique has been proven to be one of the most effective methods of modelling.
Other than that, the dynamic model of the flexible beam can be acquired using SI method. This modelling method is used to find the approximate model for flexible beam structure using real time experimental data such as input-output vibration. There are various types of model has been discovered for system identification. Among these, auto regressive exogenous (ARX) has been selected to represent the real characteristics of flexible beam. The advantages of ARX model is that it has a simple structure and requires low computational power to produce the best performance for the system [11]. SI has been implemented in many intelligence applications techniques to study the characteristics of a model structure. Swarm intelligence algorithm (SIA) has always been focused upon by researchers in the artificial intelligence field.
SIA is one of the approaches that can be applied in modelling a flexible beam to measure the parameters of the model structure. Nowadays, SIA using metaheuristic algorithm which is inspired by nature are emerging and becoming more popular. Ant Colony Optimization (ACO) algorithm is one successful examples of SIA that has been developed by M. Dorigo [12]. The ACO algorithm is inspired by the behavior of an ant colony in finding the shortest path to food source [13]. Based on a previous study done by Abusini and his colleagues (2019), they implemented the ACO algorithm to solve problems faced by integrated scheduling production and distribution [13]. Additionally, Zeron and his friends (2014) investigated the method to improve air bone pollution forecasting by using ACO [14]. Furthermore, Huang (2016) employed the ACO model in her research paper for solving continuous problems [15]. Man and Yi (2012) also proposed an improved ACO algorithm and they were used to understand the generalized traveling salesmen problem [16].
Other than that. Cuckoo Search Algorithm (CSA) which inspired by the life of cuckoo birds show a promising result in solving the optimization problems. The basic principle of this algorithm is about the specific breeding and egg laying tendencies of these birds. When the adult birds want to lay eggs, they tend to lay eggs in other bird’s habitat. The cuckoo eggs will grow safely if the eggs were not removed by the host birds. The immigration of groups of cuckoos and environmental specifications hopefully leads them to converge and get the finest place for reproduction and breeding. The objective function of this algorithm is to obtain the best place for cuckoo to lay their eggs [17]. Yang and Deb (2009) have reported their studies on cuckoo search via Levy Flights [17].
The study addresses the combination of the levy flight behavior of the birds and fruit flies with cuckoo search personality on the obligate brood parasitism [18]. Due to its interesting breeding behavior, many researchers have employed this algorithm for their studies. Ghose (2015) conducted a study on speech recognition using cuckoo search algorithm based on the destructive reproductive strategy of cuckoos [19]. Furthermore, Jiang and his partners investigated the estimation of target position by adopting cuckoo search (CS) positioning algorithm [20]. CS and ACO can solve complex computational problems and the parameters of dynamic system can be obtained accurately.
The main objective of this research is to utilize the system identification (SI) via Swarm Intelligence Algorithm (SIA) using Cuckoo Search (CS) and Ant Colony Optimization (AC) for modelling of flexible beam structure. The comparison of these models was carried out to identify the best model based on three robustness method which are correlation test, pole-zero diagram and mean squared error (MSE). The best model was chose based on the lowest MSE, correlation test within 95% confidence level and stable in pole-zero diagram. The validations are important to ensure the accuracy of the model for the controller development in cancelling the unwanted vibration using active vibration control (AVC).
2. Experimental data collection
The experimental input and output vibration data were collected by other researchers and it will be used for the modelling system via SI method. A cantilever beam was used in this experiment and the beam was separated into 20 segments with 21 nodal points. The parameters of the cantilever beam are as follows; length of 600 mm, width of 53 mm and thickness of 1 mm. They were made of aluminium. At nodal point between 8th and 9th, a disturbance actuator was place, which acts as a disturbance to make the beam vibrate. Meanwhile, a control actuator was set at nodal points between 10th and 11th. Furthermore, the detection sensor as placed between nodal points 9th and 10th while the observation sensor was placed between nodal points 19th and 20th. The input data of this system was collected at detection point and for the output experimental data at observation point. The set of input and output data were collected from a previous study [21].
3. Dynamic modelling via swarm intelligence algorithm
3.1. Ant colony optimization
In 1992, Marco Dorigo introduced a new SIA, which is ACO to solve computational problems based on travelling salesman problem [13]. This new algorithm was stimulated from the characteristics of an ant to discover the shortest distance to food source. When ants are looking for food, they automatically drop a chemical substance called pheromone on their pathway. The pheromone can be detected by other ants and will lead them to the food source. Therefore, when more ant passes on their trail, it becomes more attractive it will be followed by other ants.
Fig. 1The experimental setup for collecting input and output data [21]
![The experimental setup for collecting input and output data [21]](https://static-01.extrica.com/articles/21730/21730-img1.jpg)
Nevertheless, the basic ACO algorithm was developed using the discrete domains of the variables but due to that, it gives problems when it is related to variables laying in continuous domain. Thus, to fix the problems, ACO was extended in continuous domains. The principle of continuous ACO algorithm is still based on ACO metaheuristic without making changes of the main structure. So, the basic concept of ACO worksby advocating the construction of a solution based on the attractive pheromone solution adapted from the selection of component solutions. The discrete probability distribution was changed to continuous probability density function (PDF) in order to achieve the objective. Then, ACO employed Gaussian kernel which is a weighted summation of some Gaussian functions as PDF. Eq. (1) denote the formula of Gaussian kernel, [13]:
By derivation the th member of the population size, the th Gaussian function can be obtained. In each Gaussian function, it involves weights (), means () and standard deviations (). After that, by sampling the , a new solution is constructed. The ant is chosen probabilistically from a solution to achieve, which is proportional to weight, to develop a new solution using Eq. (2) [13]:
where is a weighted value of the solution with ranking , 1.0 for mean and is represented as standard deviation. The locality of search process, is one of the algorithm parameters which implies the weight value in solution archive. Therefore, is set as constant value, but a small value of means that the probability is biased to the best solution found whereas bigger value of gives uniform probability among solution in the solution archive. The probability of choosing the th Gaussian function is given by Eq. (3) [13]:
A new random value is generated from the chosen PDF for each dimension solution by sampling Gaussian function using the equation. In this step, mean, and standard deviation, from the PDF function are needed. The variables in each dimension of chosen solution are set as in Eq. (4) [13]:
where and the value of converge speed used 0 is same for all dimensions in algorithm parameter which is used to adjust the size of standard deviation of Gaussian function. Standard deviation is described as the radius of search space for the sampling process. If the size of radius is bigger than 1.0, it will expand the search space. Meanwhile, when the size of radius is smaller less than 1.0, it will shrink the search space. The pheromone model in ACO is completed by ranking the solution archive, . For each iteration, a new set of solutions is added to and ranked based on the fitness. In ACO, will always keep maintaining the number of populations, so it will be removed the worst set of solutions from it. This action related to the pheromone update in discrete ACO. Finally, the purpose of this is to make the search process bias towards the best solutions found during the search.
3.2. Cuckoo search algorithm
In 2009, Yang and Deb introduced another SIA namely CS. This algorithm was inspired by the behavior of cuckoo birds in placing their eggs in other birds’ species nest for survival purposes. Normally, parasitic cuckoo always aims for a nest where other bird species have just laid their own eggs. Generally, the cuckoo eggs will hatch before the host nest’s eggs, hence increasing the probability of the cuckoo chicks to receive food from the host bird. In addition, it is an advantage for the cuckoo chicks to have access to the feed since it can imitate the voice of the host bird’s nest.
The strategy from the breeding behavior of cuckoo can be used in solving the optimization problem. The solution is depicted by each egg laid in the host nest. In the meantime, a new solution is represented by a cuckoo egg. The purpose of the new solution is to establish a bigger possible solution by substituting the worse solution in the existing nest. In this study, each nest will consist of one egg since we only required a single objective function which based on MSE.
For the appropriate implementation, the cuckoo’s behavior can be idealized by considering three rules as follows [22]:
– At a time, each cuckoo lay and throws one egg at random host nest.
– The best nests that consist of high-quality eggs will be transferred to the next generation.
–The available number of host nest is fixed, and a host bird has a probability [0, 1] to recognize an alien egg. Due to this possibility, the host bird has 2 option which is either eliminates the egg or leave the nest and creates a new one in a new spot.
A set of random values in the lower and upper bound is assigned to each decision variable for the initial position of the nests. After that, the fitness is evaluated using objective function. Eq. (5) is used to calculate the initial position of each nest, [22]:
where is several nests which represent the solution within the lower and upper limits. In addition, the range between 0 and 1 is assigned to the equation and denoted as . The next stage is generation of new cuckoos which represent the solution of the optimized problem. The number of cuckoos is the same as the number of nests since each nest represents only one solution. In this study, the exploration of search space is carried out by using two techniques which are known as Levy flight and random walk. An effective exploration in generating a new solution can be obtained using Levy flight because it has a probability distribution in random step lengths. It comprises a series of straight-line flight followed by an abrupt 90° turn. The Levy flights in CSA are carried out using Eq. (6) [22]:
where is an individual current location, is the step size variable; is a random number resulting from a normal distribution and is the current best nest; and is random walk using Levy flights. A Mantegna algorithm is used to calculate the step length as shown in Eq. (7) [22]:
where is a parameter that has a range of 1 to 2 and for this study, it is considered as 1.5. The value of and can be gained from normal distribution as in Eq. (8) [22]:
The alien eggs discovery is performed for each component of each solution in terms of probability matrix as Eq. (9) [22]:
where is the discovering probability. Existing eggs are replaced considering their quality by the newly generated ones from their current positions through random walks with step size using Eq. (10) [22]:
where and are random permutation functions used for different rows permutation applied on nests matrix and is the probability matrix.
4. Results and discussions
In this study, system identification was used for modelling of the flexible beam structure by utilizing ACO and CSA. The purpose of this study was to determine the transfer function of dynamic model flexible beam structure. There were 3334 set of data collected during the experiment. From the data obtained, 3334 set of data were divided into two different categories of data, which are 1667 as training data and 1667 data as testing data. The best appropriate model was achieved through three validation steps which are MSE, 95 % confidence of correlation test and pole-zero diagram stability. Then, the results of the developed algorithm were compared to determine which algorithm is the best model.
4.1. Modelling of flexible beam using ant colony optimization (ACO) algorithm
The best model of ACO was obtained by heuristic method, which is by trial and error. In this algorithm, there were five parameters adjusted heuristically by substituting different values of population size, number of ants, intensification factor, number of iteration and model order. However, the two (2) parameters of ACO algorithm that were set as constant were the boundary [0.001, 0.001] and deviation distance factor [1]. Firstly, the tuning process was initiated by adjusting one of the parameters at one time and the other parameters was set as a constant value. Next, the other parameters were tuned until the best model of ACO algorithm was acquired. The best model of ACO algorithm was achieved when it satisfies the three validations which are lowest MSE value, has excellent correlation test and has high stability in pole zero diagram.
Table 1The best parameter result of ACO algorithm tuning
Parameter | Value |
Population size | 40 |
Number of ant | 28 |
Intensification factor | 0.001 |
Maximum iteration | 4000 |
Mean square error testing | 1.0728×10-8 |
Boundary | [–0.001 0.001] |
Deviation-distance ratio | 1 |
Model order | 3 |
Number of parameters | 6 |
Table 1 represents the result of the best model parameters obtained from the ACO modelling method. In this study, the main criteria required for the best model it was that it must achieve the lowest MSE value. Based on the tabulated results, it was recognized that model order 3 achieved the lowest MSE value which is 1.0728×10-8. Moreover, it also obtained 95 % confidence level of correlation test and has achieved good stability system in pole zero diagram. The finest model of ACO algorithm acquired can be classified as the simplest model based on the least number of parameters, which is 6.
According to Fig. 2 and 3, the developed model was capable to follow an actual measured output. Both graphs showed that the predicted output which overlapped the actual output can be declared as a good model for this system. Fig. 4 illustrates the errors of actual and predicted outputs of the system using ACO algorithm modelling. Finally, Fig. 5 and 6 shows the graph of both correlation test and stability of pole-zero diagram. The discrete transfer function obtained from the best model of ACO modelling was presented in Eq. (11):
Fig. 2Time domain for actual and predicted output of the system using ACO modelling
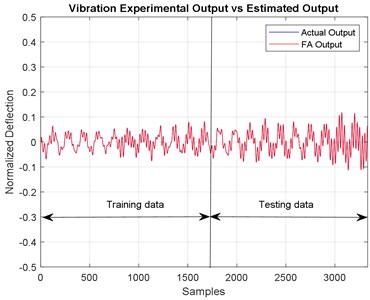
Fig. 3Frequency domain for actual and predicted output of the system using ACO modelling
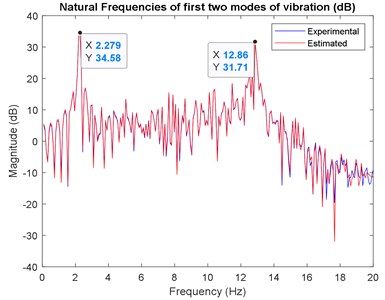
Fig. 4Errors of actual and predicted outputs of the system for ACO modelling
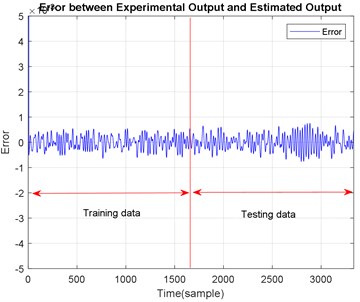
Fig. 5Correlation test for ACO: a) auto correlation, b) cross correlation
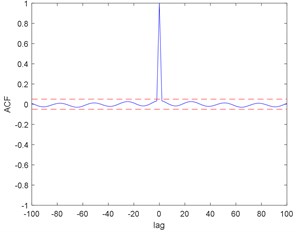
a)
b)
Fig. 6Pole-zero diagram using ACO modelling
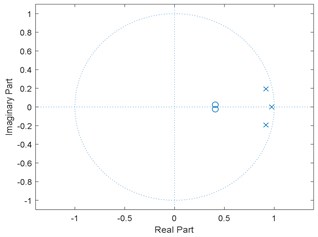
4.2. Modelling of flexible beam using Cuckoo search algorithm (CSA)
After that, there were five (5) parameters of CSA that were tuned which include the number of nests, the switching probability, lower and upper boundary, model order, and iteration. The initial tuning was focused on the CSA parameters and was followed with model order and finally the iteration. For number of nests, the values were varied from 16 to 40 while other parameters were fixed to a known value. Next, the value of switching probabilities was tuned from 0.01 until 0.5 while the number of upper and lower boundaries were tuned from [–1, 1] until [–8, 8]. In addition, the number of model order was tuned using RLS, which was 2 to 10. Finally, the iteration was tuned from 1500 to 5500 with an increment of 1000. The set of variables that has been tuned based on the heuristic method in obtaining the optimum model for a flexible beam structure via CSA was finalized and elucidated in Table 2. These parameters obtained the MSE, correlation test within a 95 % confidence level, and good stability in the pole-zero diagram.
Table 2The parameters obtained in CSA for the best flexible beam model
Parameter | Value |
No of nest | 20 |
Switch probability | 0.01 |
Lower and upper bound | [–1 1] |
Model order | 3 |
Number of parameters | 6 |
Maximum generation | 3500 |
Mean square error testing | 6.1547×10-9 |
The best CSA model managed to imitate the real system because the actual and predicted outputs overlapped with each other. This can be observed in Fig. 7 and 8 which shows the vibration experimental and simulation outputs for the system in time and frequency domains, respectively. In Fig. 8, the first mode of vibration is 2.279 dB and the error between the experimental and estimated output using CSA is highlighted in Fig. 9. The pole-zero diagram and correlation test for CSA modelling are shown in Fig. 10 and 11, respectively.
Fig. 7Time domain representation of actual and CSA outputs of the flexible beam
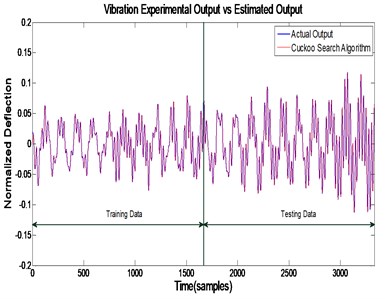
Fig. 8Frequency domain representation of actual and CSA outputs of the flexible beam
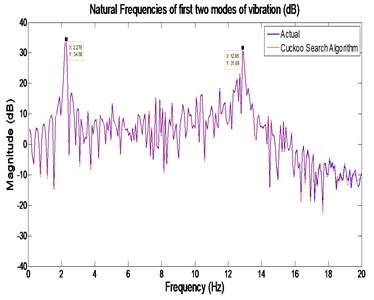
Fig. 9Errors between experimental and prediction outputs of the system for CSA modelling
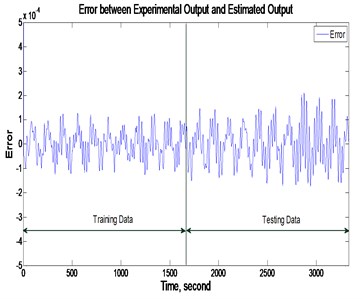
Fig. 10Pole-zero diagram stability for CSA modelling
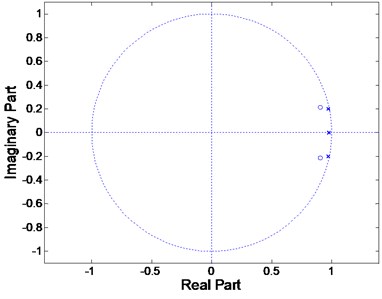
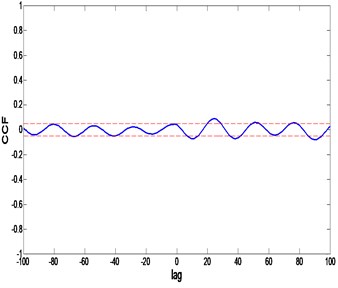
All three poles obtained from model order of 3 can be seen inside the unit circle which means that the system is stable. For the correlation test, the model was seen to be unbiased because the confidence level is between the 95 % interval. The discrete transfer function described in Eq. (12) represents the best model of flexible beam structure obtained using CSA modelling:
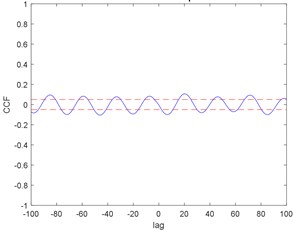
Fig. 11CSA model correlation test: a) auto-correlation, b) cross-correlation
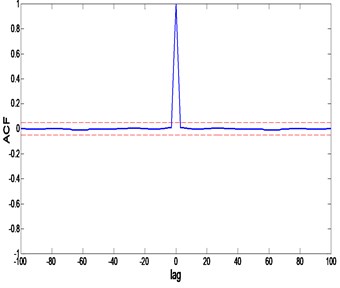
a)
b)
4.3. Comparative performance model of ACO and CSA
The performance of developed model in ACO and CSA had been compared and discussed based on the 3 criteria’s which are MSE, correlation test and pole-zero diagram stability. The validation methods were chosen as it is capable to determine the accuracy of the system in many simulation environment [23]. Table 3 is the summary of the performance of modelling flexible beam using ACO and CSA algorithms. According to Table 3, the lowest MSE value for the ACO algorithm obtained was 1.0728×10-8 while for the CSA, it was 6.1547×10-9. Based on the MSE value, CSA is a more reliable algorithm due to the lower MSE value compared to ACO algorithm. Then, developed algorithms were validated using correlation test and pole-zero diagram to select the finest algorithm.
After that, in terms of the good correlation test, the result acquired must achieve at least 95 % of confidence level. As we know, it is impossible for real applications to achieve 100 % confidence level. Based on Table 3, it shows that the result of ACO and CSA models are unbiased because both systems are within the 95 % confidence level interval. Nevertheless, for the CSA model, it still proved to be the best model so far when it compares to ACO model because it has the lowest MSE value.
Other than that, the stability of the pole zero diagram is an indicator to determine the best model for the flexible beam. Therefore, the stability of the model can be determined based on the position of poles in the pole zero diagram. So, if all the poles are inside the circle, it can be considered as the most stable model. From Table 3, ACO and CSA models show that both algorithms have stable systems. These results were obtained from the observation that all the poles managed to plot inside the circle area. So, this study proves that SIA is more reliable compared to conventional algorithm.
Table 3The summary of performance modelling flexible beam
Model | Model order | MSE | Stability | Correlation test |
Ant colony optimization (ACO) | 3 | 1.0728×10-8 | Stable | Unbiased |
Cuckoo search algorithm (CSA) | 3 | 6.1547×10-9 | Stable | Unbiased |
Despite ACO and CSA models having met the requirements as the best model to represent the behavior of flexible beam structure, CSA model is more reliable due to the lower MSE. Hence, it can be summarized that CSA model is a suitable algorithm to represent the actual flexible beam structure. CSA algorithm proved to be the best model as it had the lowest MSE value, good correlation test, high stability, and the simplest model. Hence, the CSA’s transfer function was used for the development of the controller to suppress undesired vibration on flexible beam system.
5. Conclusions
In conclusion, two developed models were designed to obtain the real characteristics of flexible beam structure based on SIA. The model for flexible beam system was successfully generated using swarm intelligence algorithm via ACO and CSA. Then, the results of modelling for both algorithms were measured based on three robustness validation tests in order to obtain the finest model that can represent the real characteristics of flexible beam structure. The three validations test, which are lowest MSE value, achieving 95 % confidence level for correlation test and exhibit excellent stability in pole-zero diagram. The models which satisfied all the three conditions was chosen as best model to represent real flexible beam in transfer function.
Moreover, the transfer function that has been obtained from the modelled flexible beam system was used in AVC to develop a good controller for vibration cancellation. From the result and discussion, the MSE value of CSA model was lower than ACO model. Nevertheless, the ACO and CSA models achieved good correlation test and have good stability in pole zero diagram. Thus, the mathematical modelling of flexible beam via CSA and ACO algorithm was successfully obtained. CSA model was chosen as the best model because it outperformed the ACO model in term of the MSE. Therefore, the objective of the studies to model a flexible beam structure using ACO and CSA as well as comparing its performance was achieved.
References
-
Saad M. S., Jamaluddin H., Darus I. Z. M. Active vibration control of flexible beam system using proportional control scheme in finite difference simulation platform. 4th International Conference on Modelling, Simulation and Applied Optimization, Kuala Lumpur, Malaysia, 2011.
-
Roshin R., Shihabudheen K. V. Mathematical modelling of flexible beam – a comparative study. International Conference on Control Communication and Computing (ICCC), Thiruvananthapuram, India, 2013, p. 325-330.
-
Choi S. B., Hoon S., Jeo J. Vibration control of flexible structures using semi-active mount: experimental investigation. Advances in Vibration Engineering and Structural Dynamics, Education in Technology, 2012.
-
Zhang D., Jia Guo J. Y., Duan Y. Research on active and passive compound vibration control based on photoelectric displacement detection. 6th World Congress on Intelligent Control and Automation, Dalian, China, 2016, p. 4948-4950.
-
Mohamad M., Tokhi M. O., Omar M. Continuous ant colony optimization for active vibration control of flexible beam structures. IEEE International Conference on Mechatronics, Istanbul, Turkey, 2011, p. 803-808.
-
Fadil M. A., Darus I. Z. M. Evolutionary algorithms for self-tuning active vibration control of flexible beam. 2013 Australian Control Conference, Fremantle, WA, Australia, 2013, p. 104-108.
-
Wang Fu Y. J., Li P., Yu M. Experimental study on fuzzy control of flexible beam using piezoelectric stack actuator. 27th Chinese Control and Decision Conference, 2015, p. 947-952.
-
Boonkumkrong Asadamongkon N. P., Chinvorarat S. Backstepping boundary control: an application to the suppression of flexible beam vibration. IOP Conference Series Materials Science and Engineering, Vol. 297, 2018, p. 012047.
-
Ros N. F. M., Saad M. S., Darus I. Z. M. Dynamic modeling and active vibration control of a flexible beam: a review. International Journal of Engineering, Vol. 15, Issue 5, 2015, p. 12-17.
-
Mirafzal S. H., Khorasani A. M., Ghasemi A. H. Optimizing time delay feedback for active vibration control of a cantilever beam using a genetic algorithm. Journal Vibration and Control, Vol. 22, Issue 19, 2016, p. 4047-4061.
-
Rahman T. A. Z., As’arry A., Jalil N. A. A. Active vibration control of a flexible beam structure using chaotic fractal search algorithm. Procedia Engineering, Vol. 170, 2017, p. 299-306.
-
Kalaivani S., Vikram A., Gopinath G. An effective swarm optimization-based intrusion detection classifier system for cloud computing. 5th International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, 2019, p. 185-188.
-
Abusini S., Sukmarini M. A., Karim C. Ant colony optimization with double selections for solving integrated scheduling problem in manufacturer. Journal of Engineering and Management in Industrial System, Vol. 7, Issue 1, 2019, p. 25-34.
-
Zeron E. M., Fernandez M. A. A., Hurtado E. G., Olmedo, A. S., Arreguín J. M. R. Method to improve airborne pollution forecasting by using ant colony optimization and neuro-fuzzy algorithms. International Journal of Intelligence Science, Vol. 4, Issue 4, 2014, p. 81-90.
-
Huang X. Ant colony optimization algorithm model based on the continuous space. International Journal of Online and Biomedical Engineering, Vol. 12, Issue 12, 2016, p. 27-31.
-
Man K. J., Yi Z. Application of an improved ant colony optimization on generalized traveling salesman problem. Energy Procedia, Vol. 17, 2012, p. 319-325.
-
Joshi A. S., Kulkarni O., Kakandikar G. M., Nandedkar V. M. Cuckoo search optimization- a review. Materials Today: Proceedings, Vol. 4, Issue 8, 2017, p. 7262-7269.
-
Yang X. S., Deb S. Cuckoo search via levy flight. World Congress on Nature and Biologically Inspired Computing, Coimbatore, 2019.
-
Ghose R., Das T., Saha A., Das T., Chattopadhyay S. P. Cuckoo search algorithm for speech recognition. International Conference and Workshop on Computing and Communication, Vancouver, 2015.
-
Jiang Y., Liu M., Chen T., Gao L. TDOA passive location based on cuckoo search algorithm. Journal of Shanghai Jiaotong University (Science), Vol. 3, Issue 23, 2015, p. 368-375.
-
Baharudin B. I., Hadi M. S., Yatim H. M., Eek R. T. P. Active Vibration Control of Flexible Beam System Based on Bio-Inspired Firefly Algorithm. Mechanical Applications: Design, Modelling and Control. 1st Edition, Penerbit UTM Press, 2020, p. 123-143.
-
Kaveh A., Bakhshpoori T., Ashoory M. An efficient optimization procedure based on cuckoo search algorithm for practical design of steel structure. International Journal of Optimization in Civil Engineering, Vol. 2, Issue 2, 2012, p. 1-14.
-
Robinson S. R., Nguyen C. T., Allen J. B. Characterizing the ear canal acoustic reflectance and impedance by pole-zero fitting. Hearing Research, Vol. 301, 2013, p. 168-182.
About this article
The authors would like to express their gratitude to Universiti Teknologi MARA (UiTM), Universiti Putra Malaysia, Universiti Teknologi Malaysia (UTM) and Ministry of Higher Education (MoHE) for funding the research and providing facilities to conduct this research. FRGS-RACER Grant with sponsor file number (RACER/1/2019/TK03/UITM//1).
