Geometrically non-linear free and forced vibration of a shallow arch

1. Introduction

Investigating the geometrical non-linearity is one of the major consideration on the design process of the arches. The study of the geometrical non-linearity of a beams, plates ,shells and circular arches were investigated by the authors of [1-8]. The authors classified the arches following their shallowness ratio into two classes; shallow arches and deep or no-shallow arches. The present study will be mainly focused on the non-linear free and forced vibration of a sinusoidal shallow arch.

Many researchers have studied the static and dynamic of shallow arch, experimentally and theoretically. Raymond H. Plaut et al. [9] determined the form of the arch which maximizes the fundamental vibration frequency.

Nayfeh et al. [10] obtained an exact solution of the eigenvalue problems governing linear undumped free vibrations of buckled beam, W. Lacarbona and G. Rega [11] obtained the general conditions for orthogonality of the non-linear modes in case of two-to-one, two-to-three, and one-to-one resonance. Using the multiple scales method, Yi Z., Stanciulescu [12] constructed the NNMs by considering the quadratic and cubic nonlinearities for a shallow arch with one end elastically restrained in vertical and rotational directions in the case of two-to-one internal resonances.

George C. Tsiatas and Nick G. Babouskos [13] investigated the linear and geometrically non-linear response of non-uniform shallow arches under a central concentrated force and they assume that the shallow arches have increased overall stiffness contrary to straight beams. The harmonic balance method and pseudo arc-length method was applied by Si-Qin Ye et al. [14] to study non-linear vibration of curved structure with non-linear boundary conditions. The author of [15] used a technique that combining harmonic balance coupled with continuation scheme to determine the solutions for an entire range of externally applied loading. The effects of a low frequency parametric excitation for a double hinged shallow arch with lateral and sinusoidal chargement of arch have been investigated by F. Lakrad, W. Schiehlen [16]. E. Ozkaya et al were analyzed the effect of different elastic springs coefficients and locations on non-linear transverse vibration of curved beam using the multiple scale method [17]. All these authors confirmed that linear and non-linear frequencies and modes shapes are sensitive to the linear initial curvature.

In this present paper, the analyze of the geometrical non-linearity in free and forced vibration of a sinusoidal shallow arch elastically restrained at the ends, will be presented following the analogous of [18, 19]. The effects of the parameters such as the initial curvature and concentrated force were examined. The theoretical model is based on the Euler-Bernoulli beam theory and the von Kármán geometrical non-linearity assumptions. Harmonic motion is assumed and the transverse displacement is expended into a series of finites spatial functions. Using Hamilton’s principle energy, the problem is reduced into a set of non-linear algebraic equations solved numerically using an approximate method the so-called second formulation. Based on multimode approach, the non-linear behavior of system can be clearly observed in the backbone curves giving the non-linear amplitude-frequency dependence of the structure. The corresponding first and second non-linear deflections and curvatures of the arch are presented.

2. Mathematical review

2.1. The governing equation

In the preset study, an Euler-Bernoulli shallow arch with initial curvature $w_0\left(x\right)$, initial rise $q$ and elastically restrained at the ends by vertical and rotational springs at left and right with stiffness coefficients $K_{t_1}$, $K_{{\theta }_1}$, $K_{t_2}$ and $K_{{\theta }_2}$ respectively. The expressions of the kinetic energy $T$, the axial strain energy $V_a$ and the bending strain energy $V_b$ of the system represented in Fig. 1 may be written as:

1

$T=\frac{1}{2}\rho A\underset{0}{\overset{L}{\int }}{\left(\frac{\partial w\left(x,t\right)}{\partial t}\right)}^{2}dx,$

2

$V_a=\frac{1}{2}EA{\left[\underset{0}{\overset{L}{\int }}\left(\frac{d{w}_0\left(x\right)}{dx}\frac{\partial w(x,t)}{\partial x}+\frac{1}{2}{\left(\frac{\partial w(x,t)}{\partial x}\right)}^2\right)dx\right]}^2,$

3

$V_b=\frac{1}{2}EI\underset{0}{\overset{L}{\int }}{\left(\frac{{\partial }^{2}w(x,t)}{\partial x^2}\right)}^{2}dx.$

The total strain energy of a shallow arch $V$ can be expressed as the sum of the axial strain energy $V_a$ and the bending strain energy $V_b$ as:

4

$V=V_a+V_b.$

where $L$ is the projected length of the beam, A cross-section, $\rho$ is the density per unit length, $I$ the moment of inertia, $E$ the modulus of elasticity, $w_0\left(x\right)$ is the initial configuration function which is assumed to be:

5

$w_0\left(x\right)=\frac{q}{2}\left(1-\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{2\pi x}{L}\right)\right).$

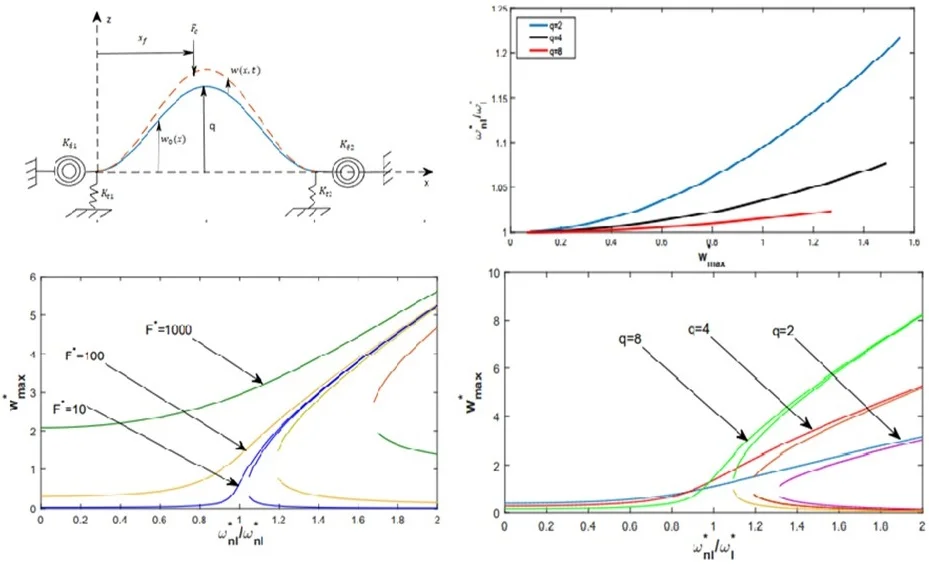
Fig. 1Schematic of vibration of a shallow arch supported by translational and rotational springs at both ends

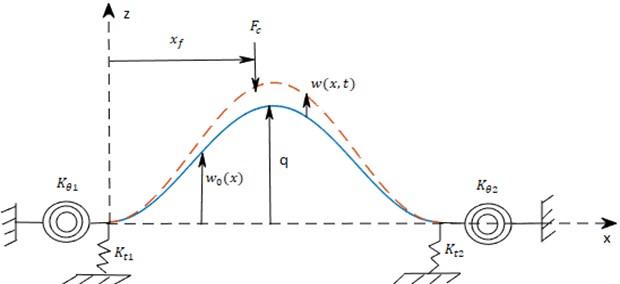
The kinetic energy Eq. (1) and total strain energy Eq. (4) due to the bending and axial strain are used in Hamilton’s principle as defined in Eq. (5) to obtain the equilibrium equation of motion of a shallow arch, the longitudinal displacement is eliminated from the equations:

6

$\partial \underset{t_1}{\overset{t_2}{\int }}\left(V-T\right)dt=0.$

The corresponding equation of motion can be written as follows:

7

$\rho A\frac{{\partial }^{2}w(x,t)}{\partial t^2}+EI\frac{{\partial }^{4}w(x,t)}{\partial x^2}=\frac{EA}{2L}\left(\frac{{\partial }^{2}w(x,t)}{\partial x^2}+\frac{d^2{w}_0\left(x\right)}{d{x}^2}\right)\underset{0}{\overset{L}{\int }}\left({\left(\frac{\partial w(x,t)}{\partial x}\right)}^2+2\frac{d{w}_0\left(x\right)}{dx}\frac{\partial w(x,t)}{\partial x}\right)dx.$

For convenience, the following non-dimensional variables are used:

8

$x^{*}=\frac{x}{L},\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}{w}^{*}=\frac{w}{r},\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}{w_0}^{*}=\frac{w_0}{r},\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}t=t^{*}\sqrt{\frac{EI}{\rho A{L}^4}},\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}{q}^{*}=\frac{q}{r},$

where $r=\sqrt{I/A}$ is the radius of gyration of the cross section, $x^{*}$ is the dimensionless length, $w^{*}\left(x\right)$ is the dimensionless deflection from the initial configuration, ${w_0}^{*}\left(x\right)$ the dimensionless initial curvature of the arch., $q^{*}$ is the dimensionless initial rise of the arch. The dimensionless equation of motion can be written as follows:

9

$\frac{{\partial }^{2}w(x,t)}{\partial t^2}+\frac{{\partial }^{4}w(x,t)}{\partial x^2}=\left(\frac{{\partial }^{2}w(x,t)}{\partial x^2}+\frac{d^2{w}_0\left(x\right)}{d{x}^2}\right)\underset{0}{\overset{1}{\int }}\left({\left(\frac{\partial w(x,t)}{\partial x}\right)}^2+2\frac{d{w}_0\left(x\right)}{dx}\frac{\partial w(x,t)}{\partial x}\right)dx.$

The stars of the dimensionless parameter of equations are vanished to simplify their rewriting. The boundary conditions of system at left rand at right and are respectively.

The left end condition:

10

$\frac{d^3{w}^{*}\left(x^{*}\right)}{d{x}^{*3}}\left|{\mathrm{}}_{x^{*}=0}\right.=-K_{t_1}{w}^{*}\left(x^{*}\right)\left|{\mathrm{}}_{x^{*}=0}=0\right.,\frac{d^2{w}^{*}\left(x^{*}\right)}{d{x}^{*2}}\left|{\mathrm{}}_{x^{*}=0}\right.=K_{{\theta }_1}\frac{d{w}^{*}\left(x^{*}\right)}{d{x}^{*}}\left|{\mathrm{}}_{x^{*}=0}=0\right..$

The right end condition:

11

$\frac{d^3{w}^{*}\left(x^{*}\right)}{d{x}^{*3}}\left|{\mathrm{}}_{x^{*}=1}\right.=K_{t_2}{w}^{*}\left(x^{*}\right)\left|{\mathrm{}}_{x^{*}=1}=0\right.,\frac{d^2{w}^{*}\left(x^{*}\right)}{d{x}^{*2}}\left|{\mathrm{}}_{x^{*}=1}\right.=-K_{{\theta }_2}\frac{d{w}^{*}\left(x^{*}\right)}{d{x}^{*}}\left|{\mathrm{}}_{x^{*}=1}=0\right..$

2.2. Linear problem

The linear mode shapes and frequencies satisfy the following differential system:

12

$\frac{{\partial }^{2}w(x,t)}{\partial t^2}+\frac{{\partial }^{4}w(x,t)}{\partial x^2}=\frac{d^2{w}_0\left(x\right)}{d{x}^2}\underset{0}{\overset{L}{\int }}\left(2\frac{d{w}_0\left(x\right)}{dx}\frac{\partial w(x,t)}{\partial x}\right)dx.$

The motion is assumed to be harmonic $w(x,t)=w\left(x\right)e^{i\omega t}$ where $i={\left(-1\right)}^{\frac{1}{2}}$, $\omega$ is the linear frequency and $w\left(x\right)$ is the mode shape function. The linear differential equation of motion becomes such bellow:

13

$\frac{d^{4}w\left(x\right)}{d{x}^4}-{\omega }^{2}w\left(x\right)=\frac{d^2{w}_0\left(x\right)}{d{x}^2}\underset{0}{\overset{1}{\int }}\frac{dw\left(x\right)}{dx}\frac{d{w}_0\left(x\right)}{dx}dx.$

The solution of the differential Eq. (13), may be written as a sum of homogenous a particular solution as [10]:

14

$w\left(x\right)=c_1\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}\left({\omega }^{\frac{1}{2}}x\right)+c_2\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{h}\left({\omega }^{\frac{1}{2}}x\right)+c_3\mathrm{c}\mathrm{o}\mathrm{s}\left({\omega }^{\frac{1}{2}}x\right)+c_4\mathrm{s}\mathrm{i}\mathrm{n}\left({\omega }^{\frac{1}{2}}x\right)+c_5\mathrm{c}\mathrm{o}\mathrm{s}\left(2\pi x\right).$

The eigenvalues system 5×5 has been determined iteratively using Newton-Raphson algorithm.

The first five frequencies dependent to the initial rise of the arch have been plotted in Fig. 2 by assuming the vertical and rotational stiffness $K_{t_1}=K_{{\theta }_1}=K_{t_2}=K_{{\theta }_2}=\infty$ and considering the initial rise of the $q$ varies in interval [0, 20].

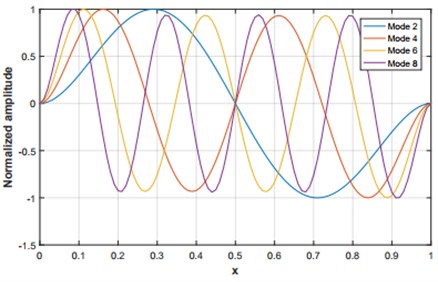
In Fig. 3 and 4 the first eight symmetrical and anti-symmetrical modes shapes are plotted respectively for a value of initial rise $q=$4.

Fig. 2Variation of the natural frequencies of the five modes of clamped-clamped shallow arch with non-dimensional rise, dash line (- -) for symmetrical modes, continuous line is for antisymmetrical modes

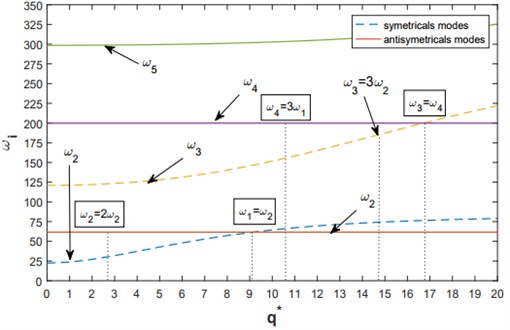
The Fig. 2 shows the variation of the frequencies with the initial dimensionless rise of the arch. We noticed that only the symmetrical mode influenced by the initial rise dimensionless of the arch. The crossing phenomena between two approaching (first order and second order modes) exists at $q=$ 9.168 and (third-order and fourth-order modes) at $q$$=$16.713. The results are compared with those given by W. Lacarbonara and G. Rega in [11] and have a very good agreement as presented in Table 1. The first four linear symmetrical and antisymmetric mode shapes of the shallow arch are plotted respectively in Fig. 3 and 4 for an initial value $q=$4.

Table 1The ratios frequencies of clamped-clamped shallow arch

Ratios	Frequencies	Present $q$	Ref. [3] $q$
1:1	${\omega }_1={\omega }_2$	9.168	9.15
1:1	${\omega }_3={\omega }_4$	16.713	16.72
2:1	${\omega }_2=2{\omega }_1$	2.788	2.79
2:1	${\omega }_3=2{\omega }_2$	3.01	3.01
3:1	${\omega }_3=3{\omega }_1$	4.975	4.98
3:1	${\omega }_4=3{\omega }_1$	10.782	10.78
3:1	${\omega }_3=3{\omega }_2$	14.712	14.70

Fig. 3Symmetrical linear displacement wi for i= 1, 3, 5 and 7 for an initial rise q= 4

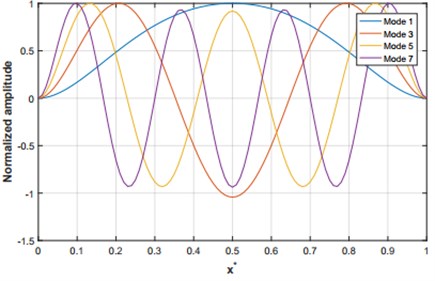
Fig. 4Anti- symmetrical linear displacement wi for i= 2, 4, 6 and 8 for an initial rise q= 4

3. Results and discussion

In this section, numerical results obtained for various values of the initial rise and levels of the excitation force will be presented via solution of the set of non-linear algebraic equations Eq. (36), based on the second formulation for the value of the stiffness of the translational and rotational springs at both ends $K_{t_1}=K_{t_2}=K_{{\theta }_1}=K_{{\theta }_2}=\infty$.

The basic functions contributions ${\epsilon }_i$ for $i$th mode shapes, the corresponding maximum non-dimensional vibration amplitudes, and the curvatures at $x=$ 0 are given in Table 2 and 3 for each given value of $a_i$. It can be seen in this tables, that the contribution $a_i$ remains predominant for the whole range of vibration amplitudes considered, compared to the contributions ${\epsilon }_i$ of the other functions, it can be noticed also that the contribution coefficients ${\epsilon }_i$ increased according to the maximum non-dimensional amplitude $w_{\mathrm{m}\mathrm{a}\mathrm{x}}^{*}$.

The numerical solutions obtained, have been substituted in Eq. (36) in case of $\left\{F_r^{*}\right\}=\left\{0\right\}$ and calculation has been made of the resulting vector {Residual}.

Fig. 5Backbone curves of clamped-clamped shallow arch, in the vicinity of the first mode, for various values of initial rises (q= 2, 4 and 8)

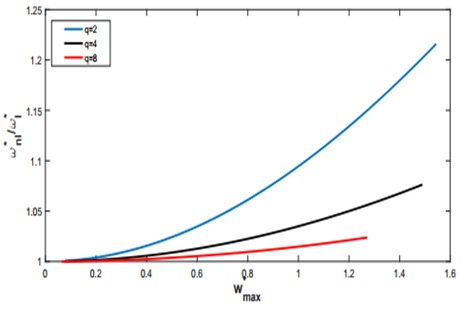
Fig. 6The first normalized non-linear mode shape for q= 4

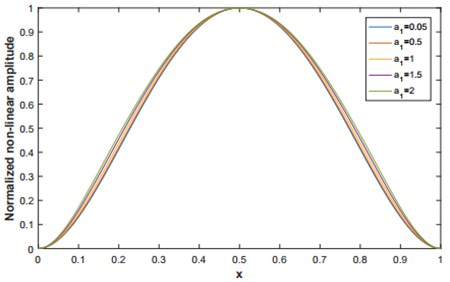
Fig. 7The second normalized non-linear mode shape for q= 4

In Fig. 5, the backbone curves giving the non-linear amplitude-frequency dependence, based on the multimode approach of a C–C shallow arch are plotted in the neighborhood of the first non-linear mode shape for various initial rise $q=$2, 4 and 8. It may be noticed that increasing the initial rise the nonlinearity decreases, these results are due to the fact that when the initial rise is increased, the flexural rigidity of the arch increases. We can also notice from the Fig. 2 that the linear frequencies of symmetrical modes increase by the increasing of the initial rise, consequently the frequency ratio decreases since the linear frequency presents the denominator of the frequency ratio. However, in the second vibration mode, the non-dimensional frequency ratios exhibit the same behavior as the straight beam. These results are compatible with the results of linear regime.

The normalized non-dimensional vibration amplitude corresponding to the first and second mode shape are presented respectively in Fig. 6 and 7.

In Fig. 8 and 9, the curvature curves of clamped-clamped shallow arch, associated to the first and second non-linear deflection are plotted for various levels of vibration amplitudes by taking into account an initial rise $q=$ 4.

Fig. 8The linear and non-linear curvature corresponding to the first mode shape for q= 4

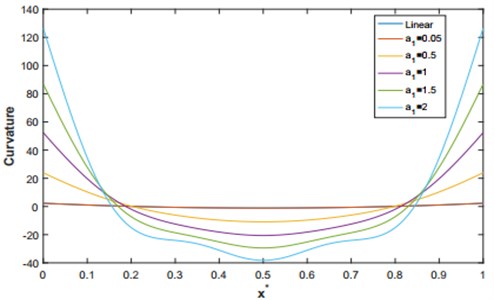
Fig. 9The linear and non-linear curvatures corresponding to the second mode shape for q= 4

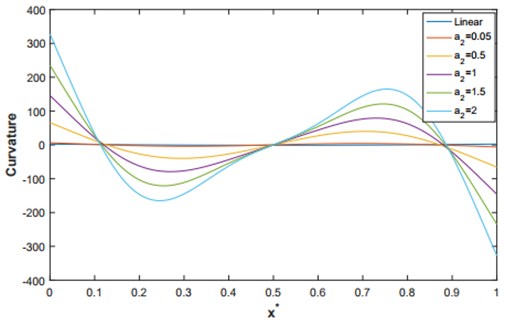
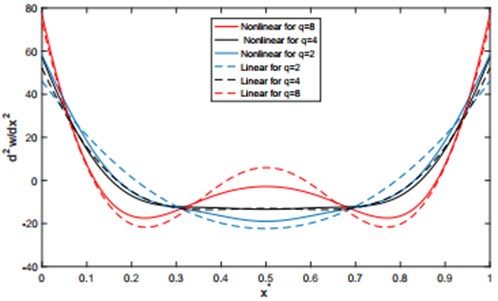
Fig. 10Curvature distributions, associated to the first non-linear deflection, of a C–C shallow arch, for various values of initial rise (q = 2, 4 and 8) and a maximum non-dimensional amplitudes wmax*=1.5

The Table 4 and 5, present the values of the non-dimensional non-linear frequency ratios and the non-dimensional vibration amplitude of clamped-clamped shallow arch which are calculated using the second formulation for various values of the initial rise 𝑞. A comparison is made with a clamped-clamped beam straight beam [4].

The Table 5 shows that the frequency ratio remains constant along the variation of initial rise of the arch. In this case the same behavior of straight beam is may be observed. It was found, that for amplitude equal to 1 time the shallow arch thickness, the difference induced does not exceed 1.8 % for the non-dimensional frequency ratio and 0.48 % for the non-dimensional vibration in comparison with the results given by [4].

In Fig. 12 and 13, the non-linear frequency response functions of the shallow arch examined, are plotted in the neighborhood of the first non-linear mode shape, for various values of the concentrated force and initial rise ($q=$ 2, 4 and 8).

In Figs. 10, the curvature distributions are plotted, associated to the first linear and non-linear deflection, of a C–C shallow arch in free vibration case, for various initial rise (2, 4, 8) and a maximum non-dimensional amplitudes $\left(w_{\mathrm{m}\mathrm{a}\mathrm{x}}^{*}=1.5\right)$. The corresponding values are summarized in Table 6, in which the percentage correction at the clamps and at the middles are given for various values of initial rise. An increase of curvature with the initial rise, especially at the clamped end of the shallow arch may be clearly observed.

Table 6 presents the calculation of the percentage correction between the curvatures via the nonlinear theory compared to the linear theory. it can be seen that the percentage correction at the middles of the arch reaches 17.74 % for $q$ = 2, 2.91 % for $q$ = 4, and 3.29 % for $q$ = 8. In addition, it can be noticed that the maximum value of the linear and nonlinear curvature of the arch in case of $q$ = 2, 4 and 8 is located near the clamped ends.

Table. 7 presents the contributions of the six symmetric modes. The calculation of the generalized forces led to the conclusion that the first mode is predominant.

The hardening behavior type of geometrical non-linearity can be clearly observed in Fig. 11-13. The discontinuities shown in Fig. 11-15 are due to the fact of the existence of three amplitudes for one range of frequency, this phenomenon is characteristic on non-linear systems, and is called a jump phenomenon. Another property of non-linear system can be clearly observed; the frequency-response functions are not proportional to the level of the concentrated forces applied.

By assuming a multimode approach used previously in [18], Eq. (37) is plotted in the neighborhood of the first non-linear mode shape in case of various values of concentrated force $F^{*}$ in Fig. 12 and various values of the initial rise $q$ in Fig. 13. Figure 11 shows a comparison between the linear and nonlinear frequency response functions, where the shallow arch is excited by a concentrated force $F^{*}=100$.

In Fig. 12 and 13 the non-linear frequency response functions of the shallow arch are plotted in the neighborhood of the first non-linear mode shape for various levels of the concentrated force and initial rise $q$. The hardening type of geometrical non-linearity of the clamped-clamped shallow arch excited by a concentrated force is decreased in a remarkable way with increasing the initial rise. This is due to the fact that when the initial rise is increased, the flexural rigidity of the arch decreases.

The response curves have been illustrated for two cases: the first, the C-C shallow arch was excited by a concentric harmonic excitation in Fig. 12 and 13, in the second, by a uniformly distributed force in Fig. 14 and 15. It may be observed from these figures, the hardening type of geometrical non-linearity also the jump phenomenon where for the same frequency range, several results are possible, as well as the non-proportional evolution of the frequency response to the intensity of excitation.

Fig. 11Linear and nonlinear frequency response functions comparison for F*= 100 and q= 2

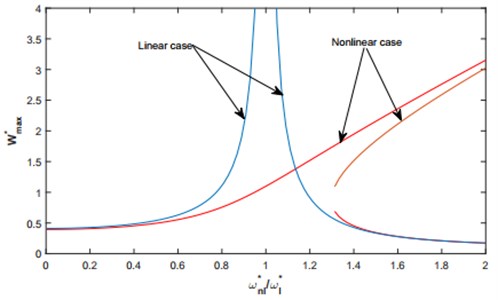
Fig. 12Nonlinear frequency response functions, based on the multimode approach, of a C-C shallow arch and various levels of the concentrated forces

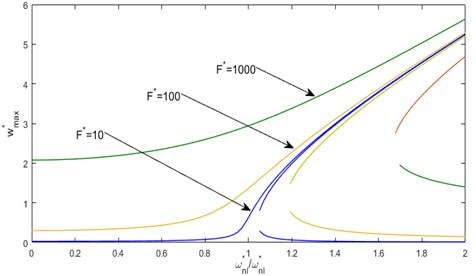
Fig. 13Nonlinear frequency response functions, based on the multimode approach, of a C-C shallow arch for a concentrated forces F*= 100 and various levels of q

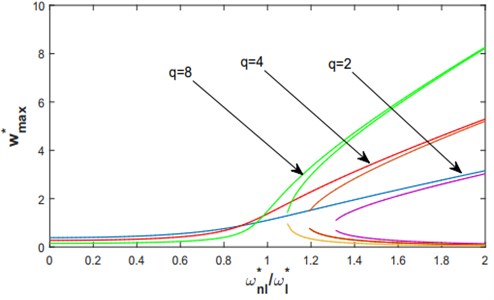
Fig. 14Nonlinear frequency response functions. based on the multimode approach. of a C-C shallow arch and various levels of excitation: in case uniformly distributed harmonic force.

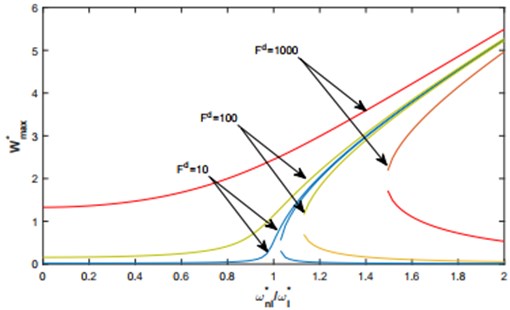
Fig. 15Nonlinear frequency response functions. based on the multimode approach. of a C-C shallow arch for a harmonic force uniformly distributed Fd=100 and various levels of q.

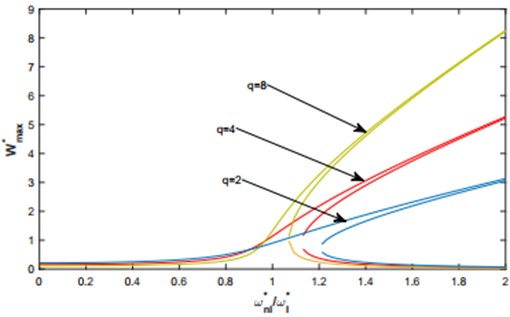
4. Conclusions

A theoretical model to analyze the large vibration amplitude of shallow arch was presented to examine the geometrical non-linearity in transverse vibration of a shallow arch. The linear frequencies were obtained iteratively using the Newton-Raphson algorithm. The mathematical formulation of the problem is based on the Euler-Bernoulli theory and the Von Karman assumptions. The kinetic and total strain energy were derived and discretized into a series of a finites spatial functions by applying Hamilton’s principle energy and spectral analysis. The problem was reduced into a set of non-linear algebraic equations solved numerically using an approximate method developed previously the so-called second formulation. The effect of the initial rise and the concentrated force on non-linear behavior of the arch was analyzed. It is found that only the symmetrical modes shapes are influenced by the initial rise, these results are due to the fact that when the initial rise is increased, the flexural rigidity of the arch increases. The passage from straight beam to curved beam is very sensitive and depends on the functionality of the future structure, but it is known that curved beam or shallow arch are very performed in case of structure which will support a higher load, because it cans resist more and avoid the earlier deflection of structure.