Artificial stepper tensile actuator using Joule-heated twisted and coiled polymer muscles

1. Introduction

Artificial muscles are linear human made actuators for linear motion requirement in some fields such as robotic, biomedical, comfort-adjusting clothing, miniature actuators for microfluidic “laboratories on a chip” etc. Low weight, low dimension, flexibility and high torque and displacement are important characteristics of these new actuators rather than ancient DC motor actuators. Artificial muscles are normally relaxed and under suitable external stimulus contract or expand. The stimuli could be a physical or chemical stimulus [1]. There are several type of artificial muscles include piezoelectric [2, 3], carbon nanotube (CNT) [4], shape memory alloys (SMAs) [5], electrochemical actuators [6], electrostatic actuators [7], pneumatic muscles (PMs) [8], and composites. Each of these actuator have some advantages and some disadvantages [9], but mainly failed to compete with mammalian muscles [9]. Recently, Haines et al. proposed an inexpensive artificial muscle with better performances that are made by twisting and coiling polymer string and some heat treatment [9]. So, they are called them twisted and coiled polymer muscles (TCPM). These muscles are inexpensive and have a large strain (~50 %) and high power to weight ratio comparable to jet engine. The muscles are made from sewing thread or fishing lines such as nylon 6, nylon 6,6 or polyethylene mono fibers. Stimulus for the muscle is heat provided by chemical reaction, fluid motion or electrical current (joule-heated). In joule-heated case, a polymer coated by silver or any conductive material is used to producing heat by electrical current. Another solution is twisted isolated (lacquered) wire on TCPM. Therefore, it’s possible to control the strain (displacement) and force using control of electrical current (or voltage) volume.

For implementation of TCPM in control systems, reliable displacement, force and temperature control of TCPM is necessary. Recently Weijde et al. proposed an inexpensive self-sensing of deflection, force and temperature for joule-heated twisted and coiled polymer muscles via electrical impedance [10]. This method does not require any bulky or expensive additional sensor and hardware. Instead electrical impedance of the coil that is dependent to coil length is used as a displacement sensor. In another work Weijde et al. completed the self-sensing method using closed-loop control of Joule-Heated TCPM [11]. They proposed a closed loop system that could control displacement and force with 95 % confidence.

Nevertheless, the closed loop control with self-sensing is relatively accurate, inexpensive and low weight but has some disadvantages. First electromagnetic interference (EMI) between coils in different TCPMs and between coils and external devices that produce electrical noise and error in displacement and force estimation. Second the method has some additional mathematic operations that need an analogue or digital computer.

Because of the disadvantages of the closed loop self-sensing method and need for quantization (stepper) displacement in non-accurate applications (low cost systems) we propose a novel stepper TCPM with quantized predictable displacement (similar to conventional stepper motors that have quantized rotation status and rotate step to step).

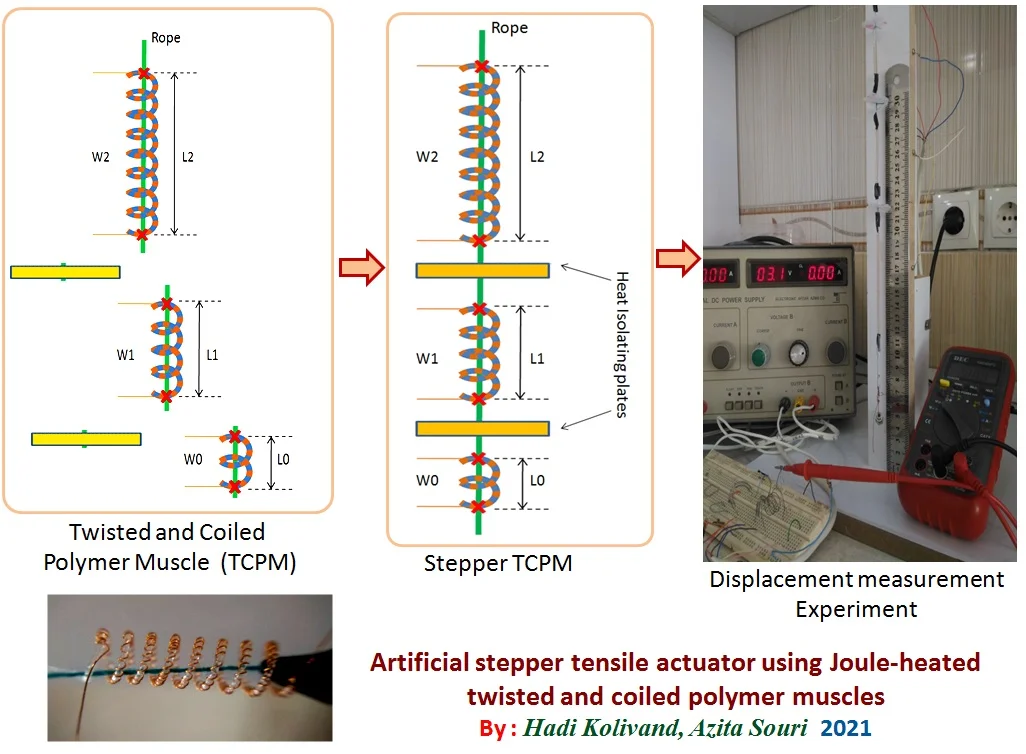
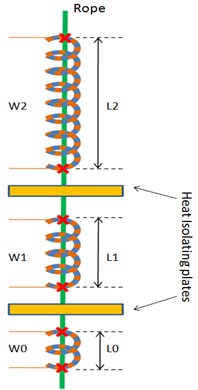
The proposed method (We name “stepper TCPM”) uses several TCPM that are connected via a miniature rope serially. In fact, the top and bottom of each TCPM (in rest mode) is tied to related section of rope. Each of these TCPM has separate winding isolated (lacquer) wires that twisted around of the TCPM fiber. The length of the each TCPM is denoted as $L_n$$(n=\mathrm{0,1},2,\dots ,N-1$) where $L_n=L_0{2}^n$and $L_0$ is length of shortest TCPM and $N$ is number of TCPMs. Also the turn of each TCPM coil is $W_n(n=\mathrm{0,1},2,\dots ,N-1)$ where $W_n=W_0{2}^n$ and $W_0$ is turn of shortest TCPM. The reason of this configuration is for ensuring maximum displacement states versus minimum number of separate TCPM.

Fig. 1 shows proposed TCPM with $n=$ 3. We can see 3 separate TCPM and its windings are indexed with $W_0$, $W_1$ and $W_2$. The length of each TCPM is half of the next TCPM and therefore can contract the related rope section. If the suitable currents (a current that cause full contraction) applied to windings with special pattern then regular stepping movement is occurred in stepper TCPM. So, the proposed stepper TCPM can be used as a stepper linear tensile actuator.

Fig. 13-bit Stepper TCPM structure (N= 3)

We will show effectiveness and simplicity of our method for stepping TCPM displacement via open loop control system. In fact, proposed TCPM can be a good replacement for conventional stepper motor linear actuator when multi step, inexpensive, low weight and flexible motion mechanism is needed.

2. Principle and fabrication of TCPM

Actuation principle of TCPM is demonstrated in different works [1, 9, 12, 13, 16]. One of the working principles of TCPM is based on simple phenomenon that relates to expansion or contraction of a twisted polymeric fiber in longitudinal or radial directions. The twisted fibers partially untwist as their diameter expands or their longitudinal axis contracts. Therefore, two contributions of “thermal untwist” can be obtained: one due to a positive radial thermal expansion coefficient and one due to a negative axial expansion coefficient. This effect can be directly exploited to obtain torsional actuators. Alternatively, linear actuators can be obtained by coiling the twisted fibers [12].

TCP muscle can be fabricated by the right procedure on the precursor fiber. Mainly two types of precursor fibers have been used in the literature. Silver-coated precursor fibers [9, 13, 14] (such as monofilament nylon 6, 6,6 and polyethylene), non-Silver-coated precursor fibers [9, 15] and precursor fibers with twisted heater wire [16]. First section of TCPM manufacturing is twisting the precursor fiber around itself while a load of optimum values is tied to it. The twisting is done using a DC motor with suitable speed that is tied to top end of fiber. Also, the optimum load is tied to bottom end of fiber and is free to move up and down but can’t rotate. The load will move up gradually under twisted fiber upward force when the fiber is rotated by DC motor. After many rotations when the fiber can’t rotate, the twisted fiber starts to coil from top or bottom of itself. Finally, rotation is stopped when whole of twisted fiber is coiled. Last procedure for TCPM is annealing. In this section twisted and coiled fiber is heated in an oven with 120 to 160 °C temperature for 30 to 60 minutes. The annealing stabilizes internal structure of twisted and coiled fiber and prevents from untwisting in room temperature. Some paper added some additional training step to accessing steady state response from TCPM (in example 12 cycles of electrical actuating with 50 % duty cycle and 20 second duration) [12, 13].

Above procedure for coiling the twisted fiber results in homochiral TCPM. This means that the TCPM in vicinity to heat will be contracted. Another method for coiling is use of a suitable mandrel. If the twisted fiber is coiled in unidirectional mode with fiber twisting direction around the mandrel, result is a homochiral TCPM. But if the coiling is done in opposite direction, we have a heterochiral TCPM that will be expanded in reaction to heat.

More detail of TCPM fabrication is investigated in literatures [9, 12-15].

3. Our method

Our method consists of two sections: fabrication of stepper joule-heated TCPM as a stepper actuator and electrical control circumstance of this actuator.

For fabricating 1-ply TCPM we use the procedure that is used extensively in the literature with a little change (little changes in turn of twisting, mass load and temperature that are elaborated in following sections). First, we use single string nylon 6 as a precursor fiber and tie top of this to a DC motor (with controllable rotation speed and minimum required torque) and bottom of this to optimum mass load. When DC motor start with soft rotation, the precursor fiber will be twisted and apply upward force to mass load. So, the mass load will rise gradually. Rotation of the motor in a critical turn must be stopped, before coiling or tearing the fiber. We measured this critical turn approximately by trial and error.

After twisting, we use very thin lacquered wire for winding twisted fiber. The winding must be monotonic and covered all cross sectional of twisted fiber homogeneously. Also twisted fiber is coiled around a metal mandrel with the unidirectional mode with fiber twisting direction for getting homochiral TCPM. Then for annealing fabricated TCPM we use an ordinary oven with 150 °C for 90 minutes. And finally in order to reach a steady state, we have applied 12 electrical actuation (420 mA current) cycles with 50 % duty cycle and 20 second duration.

We fabricated N TCPM that the length and turn of each TCPM is $L_n$ and ${\mathrm{W}}_{\mathrm{n}}$ respectively. $L_n$ and $W_n$ are calculated by Eqs. (1-2):

where $n=\mathrm{0,1},2,\dots ,N-1$ and $L_0$and $W_0$ are the length and turn of shortest TCPM, respectively.

Proposed stepper TCPM is provided from connecting these fabricated TCPMs together via a thin flexible rope serially. The top and bottom of each TCPM is tied to related section of the rope while the TCPM is in rest mode. Although we can fabricate nth TCPM a little longer than $L_n$ then push or pull it to make it equal to $L_n$ when it is tied to the rope. In another word, straight distance between up and down tie of TCPM on the rope must be $L_n$ when the rope is stretched.

Fig. 1 shows 3 bit stepper TCPM $(n=$ 3$)$. We see that there are 3 different TCPM with its windings that are tied to the rope sequentially. Also, there are heat isolating plates to prevent interferences of heat of TCPMs. In fact, because of the heat transfer between windings by air conductivity, the produced heat in a winding effects another winding and so another section of rope. This interference generates a noteworthy error in stepper TCPM displacement. One simple solution is use of insolating narrow plat (for example plastic, cloth or paper) between different windings that are located vertically related to longitude axis of stepper TCPM.

Actuating of the stepper TCPM is simple. If a pin of each winding is connected to a polarity of a power supply and another pin is connected to another polarity, then related winding and its TCPM are heated, therefore related section of the rope will be contracted. If the value of the voltage and current are greater than their thresholds, then maximum contraction (displacement) is occurred. Because of any TCPM in stepper TCPM has two states: 1-rest mode that there is no actuation and contraction 2-full actuation that full contraction is occurred, so the voltage and current values of windings must be enough for full contraction. This important rule is discussed in the next section.

For calculation of the maximum displacement of each TCPM, let consider $D_f$ and $D_w$ as diameter of twisted fiber and winding wire respectively. We have:

where ${∆L}_n$ is the maximum displacement of nth TCPM and $n=\mathrm{0,1},2,\dots ,N-1$. Also, from Eq. (1), (2) and (3) we have:

Total displacement of the stepper TCPM (or rope) $L_T$ is dependent on the displacement of TCPMs. If we consider each TCPM has two quantized states (state “0” for zero displacement and state “1” for maximum displacement), then we can calculate total displacement by sum of individual displacements:

where $m_n$ is “1” if nth TCPM is fully actuated (contracted) and is “0” if it is not actuated. We conclude from Eqs. (4) and (5):

where $DEC\left(M\right)$ is decimal of $M$ and $M$ is a binary number for displacement control of stepper TCPM.

In fact, we can control displacement of stepper TCPM by changing $M$. If $M=0$ then there is no actuation in windings and there is no displacement. In other words, if we increase $M$, the displacement is increased gradually. For more description, Table 1 shows deriving statuses of 4 windings stepper TCPM. The mark “0” means no electrical actuation (zero electrical current) and “1” means full electrical actuation (enough current to full contraction) for specified winding. Reaching to all positions (from zero to ${15∆L}_0$ step by step) is possible via Table 1. The ${∆L}_0$ indicates minimum displacement of the stepper TCPM that is similar to “Minimum Rotation Angle” of conventional stepper motor. So, driving of two actuators is similar. It means that some (or one) special windings (or winding) must be derived in a specific time for reaching the desired position.

Nevertheless, Table 1 is partly similar to conventional stepper motor deriving chart, but there is significant difference between them. A stepper motor has a sequential characteristic and its recent angle position depends on previous electrical actuations. But stepper TCPM has no memorial manner and its recent displacement depends only on recent electrical actuation.

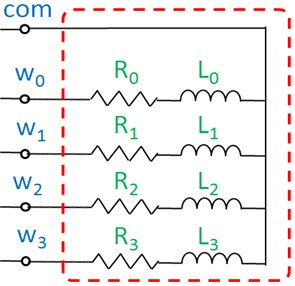
For design and implementation of electrical or electronic stepper TCPM deriver, extraction of its electrical model is necessary. So in example, we model 4 windings stepper TCPM by 4 unequal resistors and 4 non unequal inductors. Fig 2 illustrates the proposed model. The $R_n$ and $L_n$ are internal resistance and inductance of winding $W_n$respectively. For convenience, we ignore mutual inductances between inductance of the windings. Because the most of the electrical actuations are DC, we investigated the mentioned model in DC mode. In DC electrical actuation, the values of $R_n$ and $L_n$can be calculated by Eq. (7):

where $\rho$ is resistivity, $l_n$is length and $r$ is cross sectional radius of wire of $n$th winding. If cross sectional radius and material of different winding wires are equal, then below relation exists:

So, for getting equal currents and heat in each winding, using double voltages is mandatory. Therefore, applied voltages ($V_n$) must be calculated from the Eq. (9):

Determination of $V_0$as the first voltage is significant and must be calculated or measured experimentally. The large values of $V_0$ will damage the wire or fiber and small values can’t cause TCPM to fully contract. Another parameter to determining value of $V_0$ is time response of TCPM that have inverse relationship together. It means the increase of $V_0$ reduce the time of TCPM contraction and vice versa. In a paper [17] the special wave form for quick and safe response of TCPM proposed. But for convenience we use optimum DC value for $V_0$ that is measured experimentally with some trial and error.

Fig. 2Electrical model of 4 winding stepper TCPM

4. Experimental result

We have fabricated a 4 winding ($N=4$) stepper TCPM according to the mentioned method. The specification of the fibers is nylon 6 with 0.25 mm diameter and we have selected $L_0=$ 11 mm, $W_0=$ 8 turn and have calculated $L_n$ and $W_n$according to Eqs. (1), (2). But because of a fabrication error, we have errors in $L_n$ and $W_n$. Table 2 shows experimental values of manual fabricated TCPMs.

The diameter of isolated (lacquered) wires is 0.08 mm and mass of load is 100 gr and turn of twisting the fiber are about 80, 160, 320 and 680 for 4 TCPM respectively. After twisting and making each winding, we have used a metal mandrel with 4 mm diameter and 25 cm longitude for tight coiling the twisted fibers. Also, an ordinary oven is used to annealing the stepper TCPM with about 150 °C for 90 minutes. After some actuating cycles for training according to mentioned details in the previous section, finally we have used a thin rope with 0.25 mm diameter and about 400 mm longitude for tie up and down of each TCPM to it serially.

The average stepping displacement of stepper TCPM (${∆L}_0$) is calculated from Eq. (3), Table 2 data and is equal to 5.49 mm when the rope is stretched via the mass load. We have fixed the top of the stepper TCPM to a woody base and have hung a 1.5 gr metal as a mass load on it. Furthermore, an accurate ruler is placed near the stepper TCPM vertically for indication of displacement (Fig. 3).

Fig. 3a) Shortest fabricated TCPM (L0= 11 mm), b) fabricated stepper TCPM with its experimental accessories

a)

b)

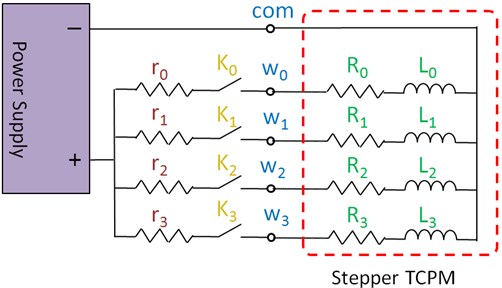
For simple electrical actuation of stepper TCPM, we have constructed an electrical circuit which includes a power supply, 4 on/off keys and 4 compensator resistors that are indexed by $r_0$, $r_1$, $r_2$, $r_3$(Fig. 4). These resistors are necessary to reach constant currents in all windings and must be calculated by Eq. (10):

where $r_{cable}$is resistance of the connection cable to power supply and is measured to be equal to 0.6 Ω. We set power supply voltage to 3 V and consider “constant” value to be 7 Ω. These voltage and resistance values get result in a current near 428 mA that is great enough to cause full contraction of TCPMs and is small enough to protect from overheating. Therefore, all values of $R_n$, $r_n$are determined. These values are showed in Table 2. For convenient all $r_n$ values are fabricated from different longitudes of a ferro Nickel wire.

In the first experiment, we have actuated stepper TCPM by electrical circuit (Fig. 4) with on/off the keys based on Table 1 ($m_3$,$m_2$,$m_1$,$m_0$ is equal to $k_3{k}_2{k}_1{k}_0$) and under conditions load mass equal to 1.5 gr and room temperature equal to 28 °C. The displacement in every step is measured after some second (2 to 6 second) delay for reaching to steady state position. These experimental results and theory displacements based on Table 1 (from $k_3{k}_2{k}_1{k}_0=$ 0000 to 1111) are plotted in Fig. 5. The comparison between two group shows that our method is relatively accurate and there is a small error (about 3.6 %) averagely. The origin of this error mainly is manual fabrication error and can be reduced considerably by auto machinery fabrication.

Fig. 4Electrical actuation circuit of stepper TCPM

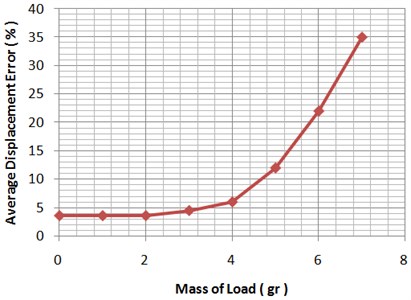
In the second experiment, the fabricated stepper TCPM is actuated electrically under different load masses and in constant temperature equal to 28 °C. The variation of mass is from 0 to 4 gr and for each mass the proposed TCPM is actuated from $k_3{k}_2{k}_1{k}_0$ equal to 0000 to 1111 and average displacement error is recorded. Average displacement errors versus load mass variation are illustrated in Fig. 6. Evident result of this plot (Fig. 6) is that the fabricated stepper TCPM can’t lift up heavy loads and is applicable from about zero gr to 4 gr mass loads. Some solutions to overcome to this inability are increasing diameter of precursor fiber, paralleling of different TCPMs etc.

Fig. 5Experimental results of displacement under electrical actuation based on Table 1 (temperature = 28 °C, mass of load = 1.5 gr)

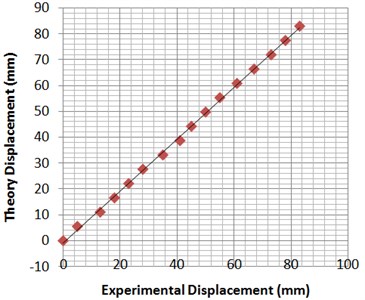
Fig. 6Average displacement error versus load mass variation in temperature = 28 °C

In the third experiment, we have repeated the second experiment but instead of mass variation, room temperature is changed from zero to 60 °C and mass of the load is kept constant at 1.5 gr. Similarly, average displacement error is recorded in each temperature. The result is illustrated in Fig. 7. There are acceptable errors (less than 4 %) in mid area from 10 to 40 °C. Intolerable errors in higher temperatures are related to overheating of TCPMs that provides more contractions. On the other hand in lower temperatures, heat generated in TCPMs is not sufficient and is wasted via cold environment.

Fig. 7Average displacement error versus room temperature variation in mass of load = 1.5 gr

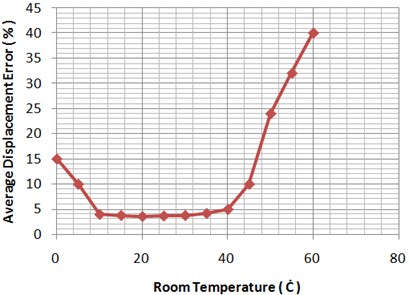
Evident result of these three experiments is that proposed stepper TCPM has almost linear displacement-input characteristic and is mass and temperature invariant in a determined range (temperature from 10 to 40 °C and mass of load from 0 to 4 gr).

5. Conclusions

In this paper we proposed new stepper joule-heated twisted and coiled polymer muscle (TCPM) that has step to step displacement under suitable electrical actuation (similar to conventional linear stepper motor). Experimental results show tolerable error, applicable frequency response in low frequency (< 1 Hz) and the effectiveness and comparability of our method. This tensile linear actuator can be a replacement for conventional stepper motor in linear movement. This actuator is low weight, high power to weigh ratio, simple and low cost rather than stepper motor. There are some disadvantages in the proposed actuator such as low frequency response, low efficiency (lesser than 10 %) and need to ventilation for coming back to normal (rest) position in hot environments. Therefore, the usage of stepper TCPM depends on the circumstance of the aim and type of the system. For example, in normal environment with determined temperature variation (10 to 40 °C), in high electrical power source systems (higher than 6 watt) and low weight (mass load smaller than 4 gr) and low-cost systems, using of the proposed stepper TCPM is recommended. Although, we can modify this actuator in higher mass loads and higher temperature conditions. Research on maximizing of the accuracy and frequency response, development of the structure and fabrication, minimizing energy consumption and extension of the application are considered as future works.